机器学习实战 3.1MNIST数据集 & 3.2训练二元分类器
3.1 mnist
下面是获取MNIST数据集的代码:
from sklearn.datasets import fetch_openml
# 从 Scikit-Learn 0.24 开始,fetch_openml() 默认返回 Pandas DataFrame。
# 为了避免这种情况并保持与书中相同的代码,我们使用 as_frame=False。
# 下载失败可以多尝试几次,初次时间会稍微稍微久一点,我等了 12min7s,再次使用会优先检查缓存文件。
mnist = fetch_openml('mnist_784',version=1)
mnist.keys()![]()
了解素材基础库:
说明这里采用的数据格式是sklearn.utils.Bunch,是一个类似字典的结构。来看一下这些数组:
说明一共有7万张图片,每张图片有784个特征。因为图片是28×28像素。每个特征代表了一个像素点的强度,从0(白色)到255(黑色)。随便取一个实例的特征向量,将其重新组成一个28×28的数组,然后使用Matplotlib的imshow()函数将其显示出来:
import matplotlib as mpl # 专业绘制图形、图像的库
import matplotlib.pyplot as plt
#原书:some_digit = X[0]
#报错:KeyError: 0
#原因:openml的MNIST数据集最近被(?)切换为返回熊猫数据帧而不是numpy数组,x是二维的,这是由于x未被视为numpy array
some_digit = X.to_numpy()[0,:]
some_digit_image = some_digit.reshape(28, 28)
plt.imshow(some_digit_image, cmap="binary") # cmap="binary" 颜色按二进制绘制
plt.axis("off") # 关闭坐标轴
plt.show()这里我们可以注意到标签是字符型,大部分机器学习算法希望是数字(为什么呢?以接下来3.2的数字5检测器为例,你的语句是“变量名字==5”,这里当然是数值的比较),那么就把 y 转成 整数:
import numpy as np
y = y.astype(np.uint8)
现在开始创建测试集,实际上,MNIST 已经分成训练集(前 6 万张图片),和测试集(最后 1 万张图片):如果你仔细看过mnist['DESCR'],里面有说明。
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]3.2训练二元分类器
现在先简化问题,只尝试识别一个数字,比如数字 5,那么这个“数字 5 检测器”就是一个二元分类器的示例,它只能区分两个类别:5和非5。先为此分类任务创建目标向量:
# 这里将得到两个由 True 和 False 组成的 列表
y_train_5 = (y_train == 5)
y_test_5 = (y_test == 5)
y_train[:20]检测一下:
y_train_5[:20]接着挑选一个分类器并开始训练,一个好的初始选择是随机梯度下降(SGD)分类器,使用Scikit-Learn的SGDClassifier类即可。这个分类器的优势是能够有效处理非常大型的数据集。这部分是因为 SGD 独立处理训练实例,一次一个(也就使得 SGD 非常适合在线学习)。此时先创建一个SGDClassifier并在整个训练集上进行训练:
from sklearn.linear_model import SGDClassifier
# 因为 SGDClassifier 是完全随机的,所以如果希望结果可复现,需要设置 random_state
# sgd_clf = SGDClassifier(random_state=42)
sgd_clf = SGDClassifier(max_iter=1000, tol=1e-3, random_state=42) # 前两个是新版默认参数
sgd_clf.fit(X_train, y_train_5)sgd_clf.predict([some_digit])说明分类器猜测这个图片是代表5的,所以输出true。下面评估一下这个分类器的性能。
3.3 性能测量
3.3.1 使用交叉验证测量准确率
使用Scikit-Learnde cross_val_score()函数来评估:
from sklearn.model_selection import cross_val_score
cross_val_score(sgd_clf, X_train, y_train_5, cv=3, scoring="accuracy")这3折结果都在93%以上。
然而如果认定一切数字都不是5,准确率也是90%以上。所以,准确率通常无法作为分类器的首要性能指标,特别是当你处理有偏数据集时(即某些类比其他类更为频繁)。
3.3.2 混淆矩阵
评估分类器,性能的更好方法是混淆矩阵,其总体思路就是统计A类别实例被分成为B类别的次数。例如,要想知道分类器将数字3和数字5混淆的次数。只需要通过混淆矩阵的第5行第3列查看。
要计算混淆矩阵,需要先有一组预测才能将其与实际目标进行比较。当然,可以通过测试集来进行预测,但是现在先不要动它(测试集最好留到项目最后,准备启动分类器时再使用)。作为替代,可以使用cross_val_predict()函数:
from sklearn.model_selection import cross_val_predict
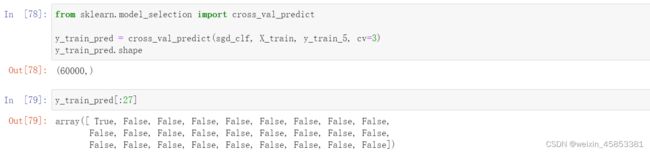
y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3)
y_train_pred.shape
y_train_pred[:27]与cross_val_score()函数一样,cross_val_predict()函数相同执行K-折交叉验证,但是返回的不是评估分数,而是每个折叠的预测。这意味着对于每个实例都可以得到一个干净的预测(“干净”的意思是模型预测时使用的数据在其训练期间从未见过)。
现在可以使用confusion_matrix()函数来获取混淆矩阵了。只需要给出目标类别(y_train_5)和预测类别(y_train_pred)即可:
from sklearn.metrics import confusion_matrix
confusion_matrix(y_train_5, y_train_pred)
混淆矩阵中的行表示实际类别,列表示预测类别。
| 混洗矩阵 | 非5(实际) | 5(实际) |
|---|---|---|
| 非5(负类) | 53892(真负类) | 687(假正类) |
| 5(正类) | 1891(假负类) | 3530(真正类) |
一个完美的分类器只有真负类和真正类,所以它的混淆矩阵只会在其对角线上有非零值。
confusion_matrix(y_train_5, y_train_5)
混淆矩阵能提供大量信息,但有时你可能希望指标更简洁一些。正类预测的准确率是一个有意思的指标,它也被称为分类器的精度。
做一个单独的正类预测,并保证它是正确的,就可以得到完美精度(1/1 = 100%)。但这没有意义,因为分类器会忽略这个正类实例之外的所有内容。因此,精度通常与另一个指标一起使用,这个指标就是召回率,也称为灵敏度或者真正类率:它是分类器正确检查到的正类实例的比例。
3.3.3 精度和召回率
我们来评估一下上面的5检测器的精度和召回率:
现在看,这个5-分类器看起来并不像它的准确率那么光线亮眼:
(1)当一张图片被判断成5时,只有83.7%的准确率;
(2)并且也只有65.1%的数字5被检查出来。
设想:将精度和召回率组合成一个单一的指标,成为F1分数。当你需要一个简单的方法来比较两种分类器时,这是个非常不错的指标。

F1分数是精度和召回率的谐波平均值。正常的平均值平等对待所有值,而谐波平均值会给予低值更高的权重。因此,只有当召回率和精度都很高时,分类器才能得到较高的F1分数。
F1分数对这些具有相近的精度和召回率的分类器更为有利。这不一定能一直符合你的期望:在某些情况下,你更关心的是精度,而另一些情况下,你可能真正关心的是召回率。
要计算F1分数,只需要调用f1_score()即可:
from sklearn.metrics import f1_score
f1_score(y_train_5, y_train_pred)
假如你训练一个分类来检测儿童可以放心观看的视频,那么你可以更青睐这种拦截了很多视频(低召回率),但是保留下来的视频都是安全(高精度)的分类器,而不是召回率虽高,但是在产品中可能会出现一些非常糟糕的视频的分类器。反过来讲,如果你训练一个分类器通过图像监控来检查小偷:你大概可以接收精度只有30%,但召回率达到99%。
遗憾的是,鱼与熊掌不可兼得,你不能同时增加精度有减少召回率,反之亦然。这称作精度/召回率权衡。
3.3.4 精度/召回率权衡
要理解这个权衡过程,我们来看看SGDClassifier如何进行分类决策的。
对于每个实例,它会基于决策函数计算出一个分值;
如果该值大于阈值,则将该实例判为正类,否则便将其判为负类;
Scikit-Learn不允许直接设置阈值,但是可以访问它用于预测的决策分数。不是调用分类器的predict()方法,而是调用decision_funcion()方法。这种方法返回每个实例的分数,然后就可以根据这些分数,使用任意阈值进行预测了:
上面证明了提高阈值的确可以降低召回率。这张图的确是 5,当阈值为0时,分类器可以检测到这个值(True),但是当阈值提高到 8000 时,就错过了这张图。
那么要如何决定使用什么阈值呢?首先,使用cross_val_predick()函数获取训练集中所有实例的分数,但是这次需要返回的是决策分数而不是预测结果:
有了这些分数,可以使用precision_recall_curve()函数来计算所有可能的阈值的精度和召回率:
from sklearn.metrics import precision_recall_curve
# 准确率、召回率、阈值:返回值按 准确率 从低到高 排序
precisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores)
def plot_precision_recall_vs_threshold(precisions, recalls, thresholds):
plt.plot(thresholds, precisions[:-1], "b--", label="Precision", linewidth=2)
plt.plot(thresholds, recalls[:-1], "g-", label="Recall", linewidth=2)
plt.legend(loc="center right", fontsize=16) # 显示图例,位置 中右
plt.xlabel("Threshold", fontsize=16) # X轴命名
plt.grid(True) # 显示网格
plt.axis([-50000, 50000, 0, 1]) # 坐标显示 X轴范围 -50000~50000;Y轴范围 0~1
recall_90_precision = recalls[np.argmax(precisions >= 0.90)] # 当准确率第一次大于0.90时的召回率。
threshold_90_precision = thresholds[np.argmax(precisions >= 0.90)] # 当准确率第一次大于0.90时的阈值。
plt.figure(figsize=(8, 4)) # 指定figure的宽和高,单位为英寸
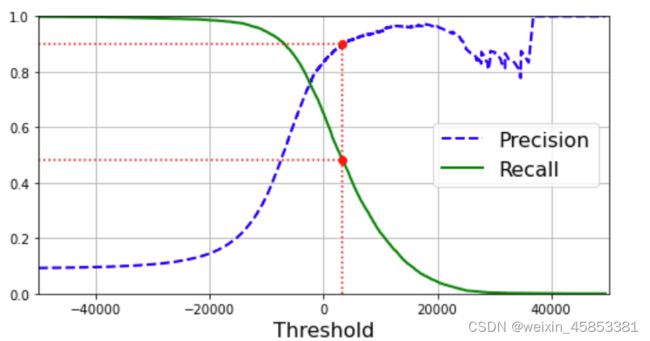
plot_precision_recall_vs_threshold(precisions, recalls, thresholds)
plt.plot([threshold_90_precision, threshold_90_precision], [0., 0.9], "r:")
plt.plot([-50000, threshold_90_precision], [0.9, 0.9], "r:")
plt.plot([-50000, threshold_90_precision], [recall_90_precision, recall_90_precision], "r:")
plt.plot([threshold_90_precision], [0.9], "ro")
plt.plot([threshold_90_precision], [recall_90_precision], "ro")
plt.show()上图中,精确率后面有明显的崎岖,原因在于,当你提高阈值时,精度有时也有可能会下降(尽管整体上是上升趋势)。所以并不是阈值越高越好。另一方面,当阈值上升时,召回率只会下降,所以它看起来很平滑。
PR曲线(精度/召回率曲线)
另一种找到好的精度/召回率权衡的方法是直接绘制精度和召回率的函数图:
def plot_precision_vs_recall(precisions, recalls):
plt.plot(recalls, precisions, "b-", linewidth=2)
plt.xlabel("Recall", fontsize=16)
plt.ylabel("Precision", fontsize=16)
plt.axis([0, 1, 0, 1])
plt.grid(True)
plt.figure(figsize=(8, 6))
plot_precision_vs_recall(precisions, recalls)
plt.plot([recall_90_precision, recall_90_precision], [0., 0.9], "r:")
plt.plot([0.0, recall_90_precision], [0.9, 0.9], "r:")
plt.plot([recall_90_precision], [0.9], "ro")
plt.show()从图中可以看到,从80%的召回率往右,精度开始急剧下降。你可能会尽量在这个陡降之前选择一个精度/召回率权衡–比如召回率60%。然后,如何选择取决于你的项目。假设你决定将精度设为90%:
threshold_90_precision # 精度为90%时的阈值
要进行预测(现在是在训练集上),除了调用分类器的predict()方法,也可以运行这段代码:
y_train_pred_90 = (y_scores >= threshold_90_precision)
# 精度、召回率
precision_score(y_train_5, y_train_pred_90), recall_score(y_train_5, y_train_pred_90)![]()
这样你就有一个90%精度的分类器了!
3.3.5 ROC曲线
还有一种经常与二元分类器一起使用的工具,叫做受试者工作特征曲线(简称 ROC)。它与精度/召回率曲线非常类似,但绘制得不是精度和召回率,而是真正类率(召回率的另一名称)和假正类率(FPR)。
1、假正类率(FPR):是被错误分为正类的负类实例比例。它等于1减去真负类率(TNR);
2、真负类率(TNR):是被正确分类为负类的负类实例比例,也成为特异度。3、因此,ROC 曲线绘制的是灵敏度(召回率)和(1 - 特异度)的关系。
要绘制 ROC 曲线,首先需要使用roc_curve()函数计算多种阈值的 TPR 和 FPR:
from sklearn.metrics import roc_curve
fpr, tpr, thresholds = roc_curve(y_train_5, y_scores)然后,使用Matplotlib绘制 FPR 对 TPR 的曲线:
def plot_roc_curve(fpr, tpr, label=None):
plt.plot(fpr, tpr, linewidth=2, label=label)
plt.plot([0, 1], [0, 1], 'k--') # 绘制对角虚线
plt.axis([0, 1, 0, 1]) # X、Y轴范围均为 0~1
plt.xlabel('False Positive Rate (Fall-Out)', fontsize=16) # 假正率
plt.ylabel('True Positive Rate (Recall)', fontsize=16) # 真正率(召回率)
plt.grid(True)
plt.figure(figsize=(8, 6))
plot_roc_curve(fpr, tpr)
fpr_90 = fpr[np.argmax(tpr >= recall_90_precision)] # 准确率90%时,召回率的位置
plt.plot([fpr_90, fpr_90], [0., recall_90_precision], "r:")
plt.plot([0.0, fpr_90], [recall_90_precision, recall_90_precision], "r:")
plt.plot([fpr_90], [recall_90_precision], "ro")
plt.show()
同样这里再次面临一个折中权衡:召回率(TPR)越高,分类器产生的假正率(FPR)就越高。虚线表示纯随机分类器的 ROC 曲线、一个优秀的分类器应该离这条线越远越好(像左上角)。
有一种比较分类器的方法,是测量曲线下面积(AUC)。完美的分类器的 ROC AUC 等于 1,而纯粹随机分类器的 ROC AUC 等于 0.5。Scikit-Learn提供计算 ROC AUC 的函数:
#比较好坏
from sklearn.metrics import roc_auc_score
roc_auc_score(y_train_5, y_scores)![]()
ROC 曲线和 PR 曲线非常类似,如何选择呢?有一个经验法则是:当正类非常少见或者你更关注假正类而不是假负类时,应该选择 PR 曲线,反之则是 ROC 曲线。
现在我们来训练一个RandomForestClassifier分类器,并比较它和SGDClassifier分类器的 ROC 曲线和 ROC AUC 分数。
首先,获取训练集中每个实例的分数。但是由于它的工作方式不同,RandomForestClassifier类没有decision_function()方法,相反,它有predict_proba()方法。Scikit-Learn的分类器通常都有这两种方法的一种(或两种都有)。
predict_proba()方法:返回一个数组,其中一行代表一个实例,每一列代表一个类别,意思是某个给定实例属于某个给定列表的概率(例如,这种图片 70% 可能是数字 5)
from sklearn.ensemble import RandomForestClassifier
# 耗时 50秒左右
forest_clf = RandomForestClassifier(random_state=42)
y_probas_forest = cross_val_predict(forest_clf, X_train, y_train_5, cv=3, method="predict_proba")
y_probas_forest[:10]
y_scores_forest = y_probas_forest[:, 1]
fpr_forest, tpr_forest, thresholds_forest = roc_curve(y_train_5, y_scores_forest)
recall_for_forest = tpr_forest[np.argmax(fpr_forest >= fpr_90)]
plt.figure(figsize=(8, 6))
plt.plot(fpr, tpr, "b:", linewidth=2, label="SGD")
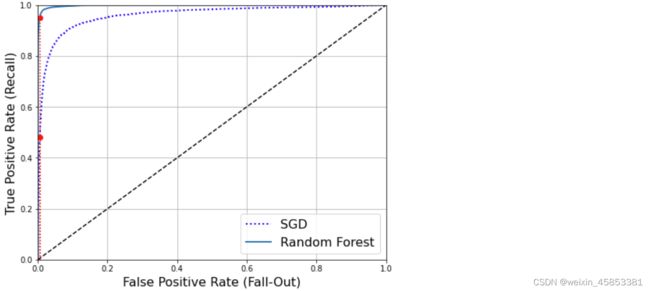
plot_roc_curve(fpr_forest, tpr_forest, "Random Forest")
plt.plot([fpr_90, fpr_90], [0., recall_90_precision], "r:")
plt.plot([0.0, fpr_90], [recall_90_precision, recall_90_precision], "r:")
plt.plot([fpr_90], [recall_90_precision], "ro")
plt.plot([fpr_90, fpr_90], [0., recall_for_forest], "r:")
plt.plot([fpr_90], [recall_for_forest], "ro")
plt.grid(True)
plt.legend(loc="lower right", fontsize=16)
plt.show()
上面数据表明随机森林分类器优于SGD分类器,ROC AUC 分数更高,99%的精度和86.8%的召回率,还不错!