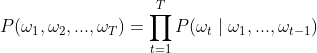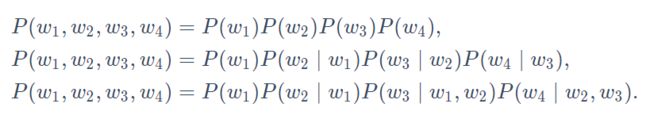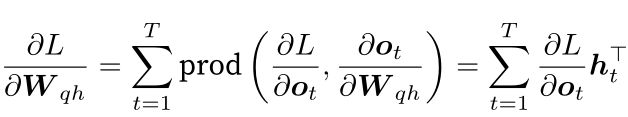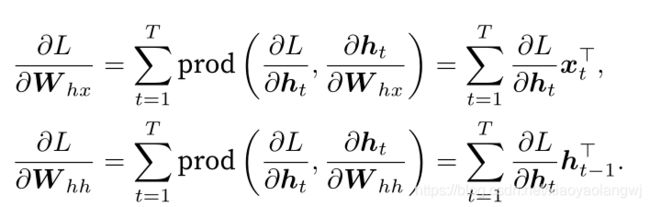《动手学深度学习》学习笔记(六)
第六章 循环神经网络
与之前介绍的多层感知机和能有效处理空间信息的卷积神经网络不同，循环神经网络是为更好地处理时序信息而设计的。
它引入状态变量来存储过去的信息，并用其与当前的输入共同决定当前的输出。
循环神经网络常用于处理序列数据，如一段文字或声音、购物或观影的顺序，甚至是图像中的一行或一列像素。因此，循环神经网络有着极为广泛的实际应用，如语言模型、文本分类、机器翻译、语音识别、图像分析、手写识别和推荐系统。
本章中的应用是基于语言模型的，所以我们将先介绍语言模型的基本概念，并由此激发循环神经网络的设计灵感。接着，我们将描述循环神经网络中的梯度计算方法，从而探究循环神经网络训练可能存在的问题。对于其中的部分问题，我们可以使用本章稍后介绍的含门控的循环神经网络来解决。最后，我们将拓展循环神经网络的架构。
一、语言模型：
语言模型（language model）是自然语言处理(NLP)的重要技术。自然语言处理中最常见的数据是文本数据。我们可以把一段自然语言文本看作一段离散的时间序列。假设一段长度为T的文本中的词依次为
,那么在离散的时间序列中，
可看作在时间步(time step) t 的输出或标签。给定一个长度为T的词的序列，语言模型将计算该序列的概率：
。
语言模型可用于提升语音识别和机器翻译的性能。
例如，在语音识别中，给定一段“厨房里食油用完了”的语音，有可能会输出“厨房里食油用完了”和“厨房里石油用完了”这两个读音完全一样的文本序列。如果语言模型判断出前者的概率大于后者的概率，我们就可以根据相同读音的语音输出“厨房里食油用完了”的文本序列。
在机器翻译中，如果对英文“you go first”逐词翻译成中文的话，可能得到“你走先”“你先走”等排列方式的文本序列。如果语言模型判断出“你先走”的概率大于其他排列方式的文本序列的概率，我们就可以把“you go first”翻译成“你先走”。
类似于分类softmax，哪个概率大，输出哪个类别。
1、语言模型的计算：
语言模型计算方法：假设序列中的每个词是依次生成的，我们有
。
一段含有4个词的文本序列的概率：
。
为了计算语言模型，我们需要计算词的概率，以及一个词在给定前几个词的情况下的条件概率，即语言模型参数。设训练数据集为一个大型文本语料库，如维基百科的所有条目。词的概率可以通过该词在训练数据集中的相对词频来计算。例如，P(w1)可以计算为w1在训练数据集中的词频（词出现的次数）与训练数据集的总词数之比。因此，根据条件概率定义，一个词在给定前几个词的情况下的条件概率也可以通过训练数据集中的相对词频计算。例如，P(w2∣w1)可以计算为w1,w2两词相邻的频率与w1词频的比值，因为该比值即P(w1,w2)与P(w1)之比；而P(w3∣w1,w2)同理可以计算为w1、w2和w3三词相邻的频率与w1和w2两词相邻的频率的比值。以此类推。
2、n元语法：
当序列长度增加时，计算和存储多个词共同出现的概率的复杂度会呈指数级增加。n元语法通过马尔可夫假设（虽然并不一定成立）简化了语言模型的计算。这里的马尔可夫假设是指一个词的出现只与前面n个词相关，即n阶马尔可夫链（Markov chain of order n）。
一个词的出现只与前面n个词相关——马尔科夫假设。
切断长链，因为太长的链，前后关系不再紧密，或者说数值太小。只取与之最近的n个元素。
过长的链，需要运算和存储大量的词频和多词相邻频率。
如果n = 1,那么有
。第三个值，只于第二个值有关。第T个值，只与T-1那个值有关。如果基于n-1阶马尔科夫链，我们可以将语言模型改写为
。以上也叫n元语法(n-grams)。它是基于n-1阶马尔科夫链的概率语言模型。当n分别为1、2和3时，我们将其分别称作一元语法(unigram)、二元语法(bigram)和三元语法(trigram)。
长度为4的序列w1,w2,w3,w4在一元语法、二元语法和三元语法中的概率分别为
n元语法的Trade-off。
-
当n较小时，nnn元语法往往并不准确。例如，在一元语法中，由三个词组成的句子“你走先”和“你先走”的概率是一样的。
-
当n较大时，n元语法需要计算并存储大量的词频和多词相邻频率。
小结：
-
语言模型是自然语言处理的重要技术。
-
N元语法是基于n−1阶马尔可夫链的概率语言模型，其中n权衡了计算复杂度和模型准确性。
二、循环神经网络：
上一节介绍的n元语法中，时间步 t 的词 
基于前面所有词的条件概率只考虑了最近时间步的 n−1 个词。如果要考虑比 t−(n−1) 更早时间步的词对 的可能影响，我们需要增大n。但这样模型参数的数量将随之呈指数级增长。
本节将介绍循环神经网络。它并非刚性地记忆所有固定长度的序列，而是通过隐藏状态来存储之前时间步的信息。首先我们回忆一下前面介绍过的多层感知机，然后描述如何添加隐藏状态来将它变成循环神经网络。
1、不含隐藏状态的神经网络
我们考虑一个含但隐藏层的多层感知机。隐藏层输出：
。输出层输出为
。如果是分类问题，使用softmax(O)来计算输出类别的概率分布。
2、含隐藏状态的循环神经网络
现在我们考虑输入数据存在时间相关性的情况：
假设
是序列中时间步为 t 的小批量输入，
是该时间步的隐藏变量。与多层感知机不同的是，这里我们保存上一步时间步的隐藏变量
，并引入一个新的权重参数
，该参数用来描述在当前时间步如何使用上一时间步的隐藏变量。
具体来说，时间步 t 的隐藏变量的计算由当前时间步的输⼊和上⼀时间步的隐藏变量共同决定：
。
与多层感知机相比，我们在这里添加了
一项。
由上式中相邻时间步的隐藏变量 和 之间的关系可知，这里的隐藏变量能够捕捉截止至当前时间步的序列的历史信息，就像是神经网络当前时间步的状态或记忆一样。因此，该隐藏变量也称为隐藏状态。
由于隐藏状态在当前时间步的定义使用了上一时间步的隐藏状态，上式的计算是循环的。使用循环计算的网络即循环神经网络（recurrent neural network）RNN。
在时间步 t，输出层的输出和多层感知机中的计算类似：
。
即便在不同时间步，循环神经网络也始终使用这些模型参数。因此，循环神经网络模型参数的数量不随时间步的增加而增长。
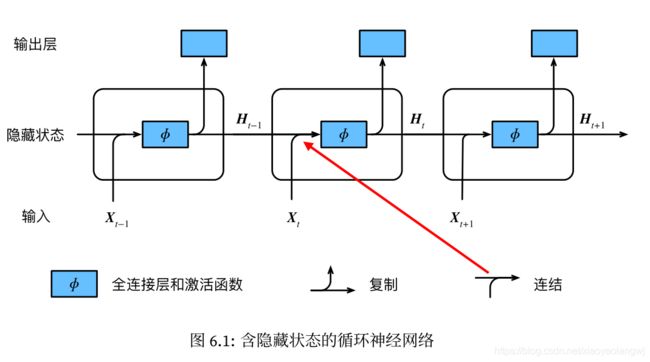
图6.1展示了循环神经网络在3个相邻时间步的计算逻辑。
在时间步t，隐藏状态的计算可以看成是将输入和前一时间步隐藏状态连结后输入一个激活函数为 ϕ 的全连接层。该全连接层的输出就是当前时间步的隐藏状态，且模型参数为
与
的连结，偏差为
。当前时间步t的隐藏状态
将参与下一个时间步t+1的隐藏状态
的计算，并输入到当前时间步的全连接输出层。
隐藏状态中
的计算等价于与连结后的矩阵乘以与连结后的矩阵。
3、应用：基于字符级循环神经网络的语言模型
因为每个输入词是一个字符，因此这个模型被称为字符级循环神经网络（character-level recurrent neural network）。因为不同字符的个数远小于不同词的个数（对于英文尤其如此），所以字符级循环神经网络的计算通常更加简单。在接下来的几节里，我们将介绍它的具体实现。
小结：
-
使用循环计算的网络即循环神经网络。
-
循环神经网络的隐藏状态可以捕捉截至当前时间步的序列的历史信息。
-
循环神经网络模型参数的数量不随时间步的增加而增长。
-
可以基于字符级循环神经网络来创建语言模型。
三、语言模型数据集：
数据集准备周杰伦第一张专辑到第十张专辑的歌词。
1、读取数据集
import torch
import random
import zipfile
with zipfile.ZipFile('../../data/jaychou_lyrics.txt.zip') as zin:
with zin.open('jaychou_lyrics.txt') as f:
corpus_chars = f.read().decode('utf-8')
corpus_chars[:40]'想要有直升机\n想要和你飞到宇宙去\n想要和你融化在一起\n融化在宇宙里\n我每天每天每'这个数据集有6万多个字符。为了打印方便，我们把换行符替换成空格，然后仅使用前1万个字符来训练模型。
corpus_chars = corpus_chars.replace('\n', ' ').replace('\r', ' ')
corpus_chars = corpus_chars[0:10000]2、建立字符索引
我们将每个字符映射成一个从0开始的连续整数，又称索引，来方便之后的数据处理。为了得到索引，我们将数据集里所有不同字符取出来，然后将其逐一映射到索引来构造词典。接着，打印vocab_size，即词典中不同字符的个数，又称词典大小。
# 二、建立字符索引
# 每个字符映射成一个从0开始的连续整数，又称索引，来方便数据处理。为建立字符，将不同字符取出来，逐一映射到索引来构造词典。
idx_to_char = list(set(corpus_chars)) # 集合set的形式去重。得到最大索引值下的无序字符列表。此时，列表中字符的排序位置，就是索引。
char_to_idx = dict([(char, i) for i, char in enumerate(idx_to_char)])
vocab_size = len(char_to_idx) # 字典长度，即索引个数。一个字符一个数字。一一对应。
print(vocab_size) # 1027
print(char_to_idx["每"]) # {“每”：621},结构是“字符”：value=idx。
print(char_to_idx["想"]) # 特别说明一点：因为上面的是set形式，无法保证有序，所以每次运行结果都不一样。
print(idx_to_char[883]) # 想
# 输出为：
# 1027
# 136
# 883
# 想之后，将训练数据集中每个字符转化为索引，并打印前20个字符及其对应的索引。
# 上面是是字典形式的索引。将歌词字符转化为数字索引。
corpus_indices = [char_to_idx[char] for char in corpus_chars]
sample = corpus_indices[:20]
print("chars:", " ".join([idx_to_char[idx] for idx in sample]))
print("indices:", sample)
# corpus_indices列表中，将歌词中每个字符按照歌词顺序corpus_chars（歌词排序）排列。
# 换句话说，将歌词转成一串数字。chars: 想要有直升机 想要和你飞到宇宙去 想要和
indices: [250, 164, 576, 421, 674, 653, 357, 250, 164, 850, 217, 910, 1012, 261, 275, 366, 357, 250, 164, 850] 我们将以上代码封装在d2lzh_pytorch包里的load_data_jay_lyrics函数中，以方便后面章节调用。调用该函数后会依次得到corpus_indices、char_to_idx、idx_to_char和vocab_size这4个变量。
- corpus_indices：语料库列表。完全按照歌词顺序将字符转成idx索引。可以理解为训练集元素索引列表。(len-1)除以时间步数，就是总样本数。
- char_to_idx：语料库索引字典。字典中key为字符，value为索引数字。
- idx_to_char：列表元素为字符。每个字符的位置索引，即为索引编号。
- vocab_size：所有字符去重之后的个数。总共有这么多个索引。词典大小。也是one-hot向量长度。
3、时序数据的采样
在训练中我们需要每次随机读取小批量样本和标签。与之前章节的实验数据不同的是，时序数据的一个样本通常包含连续的字符。
假设时间步数为5，
- 样本序列为5个字符，即“想”“要”“有”“直”“升”。
- 样本的标签序列为这些字符分别在训练集中的下一个字符，即“要”“有”“直”“升”“机”。
我们有两种方式对时序数据进行采样，分别是随机采样和相邻采样。
1）随机采样：
每次从数据里随机采样⼀个小批量。其中批量大小batch_size指每个小批量的样本数，num_steps为每个样本所包含的时间步数。在随机采样中，每个样本是原始序列上任意截取的一段序列。相邻的两个随机小批量在原始序列上的位置不一定相毗邻。因此，我们无法用一个小批量最终时间步的隐藏状态来初始化下一个小批量的隐藏状态。
在训练模型时，每次随机采样前都需要重新初始化隐藏状态。
# 本函数已保存在d2lzh_pytorch包中方便以后使用
def data_iter_random(corpus_indices, batch_size, num_steps, device=None):
# 减1是因为输出的索引x是相应输入的索引y加1
num_examples = (len(corpus_indices) - 1) // num_steps
epoch_size = num_examples // batch_size
example_indices = list(range(num_examples))
random.shuffle(example_indices)
# 返回从pos开始的长为num_steps的序列
def _data(pos):
return corpus_indices[pos: pos + num_steps]
if device is None:
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
for i in range(epoch_size):
# 每次读取batch_size个随机样本
i = i * batch_size
batch_indices = example_indices[i: i + batch_size]
X = [_data(j * num_steps) for j in batch_indices]
Y = [_data(j * num_steps + 1) for j in batch_indices]
yield torch.tensor(X, dtype=torch.float32, device=device), torch.tensor(Y, dtype=torch.float32, device=device)my_seq = list(range(30))
for X, Y in data_iter_random(my_seq, batch_size=2, num_steps=6):
print('X: ', X, '\nY:', Y, '\n')X: tensor([[18., 19., 20., 21., 22., 23.],
[12., 13., 14., 15., 16., 17.]])
Y: tensor([[19., 20., 21., 22., 23., 24.],
[13., 14., 15., 16., 17., 18.]])
X: tensor([[ 0., 1., 2., 3., 4., 5.],
[ 6., 7., 8., 9., 10., 11.]])
Y: tensor([[ 1., 2., 3., 4., 5., 6.],
[ 7., 8., 9., 10., 11., 12.]]) 2）相邻采样：
除对原始序列做随机采样之外，我们还可以令相邻的两个随机小批量在原始序列上的位置相毗邻。这时候，我们就可以用一个小批量最终时间步的隐藏状态来初始化下一个小批量的隐藏状态，从而使下一个小批量的输出也取决于当前小批量的输入，并如此循环下去。
这对实现循环神经网络造成了两方面影响：
- 一方面， 在训练模型时，我们只需在每一个迭代周期开始时初始化隐藏状态；
- 一方面，当多个相邻小批量通过传递隐藏状态串联起来时，模型参数的梯度计算将依赖所有串联起来的小批量序列。同一迭代周期中，随着迭代次数的增加，梯度的计算开销会越来越大。
# 本函数已保存在d2lzh_pytorch包中方便以后使用
def data_iter_consecutive(corpus_indices, batch_size, num_steps, device=None):
if device is None:
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
corpus_indices = torch.tensor(corpus_indices, dtype=torch.float32, device=device)
data_len = len(corpus_indices)
batch_len = data_len // batch_size
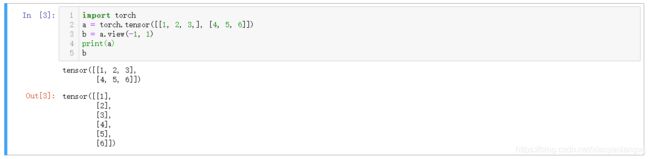
indices = corpus_indices[0: batch_size*batch_len].view(batch_size, batch_len)
# view()其作用在于返回和原tensor数据个数相同，但size不同的tensor。相当于numpy中的reshape。 -1表示维数自动判断。
epoch_size = (batch_len - 1) // num_steps
for i in range(epoch_size):
i = i * num_steps
X = indices[:, i: i + num_steps]
Y = indices[:, i + 1: i + num_steps + 1]
yield X, Y
补充一波：view的用法。
a和b其实在内存中是共享的。
此处与view效果等效的是unsqueeze函数。
同样的设置下，打印相邻采样每次读取的小批量样本的输入X和标签Y。相邻的两个随机小批量在原始序列上的位置相毗邻。
for X, Y in data_iter_consecutive(my_seq, batch_size=2, num_steps=6):
print('X: ', X, '\nY:', Y, '\n')X: tensor([[ 0., 1., 2., 3., 4., 5.],
[15., 16., 17., 18., 19., 20.]])
Y: tensor([[ 1., 2., 3., 4., 5., 6.],
[16., 17., 18., 19., 20., 21.]])
X: tensor([[ 6., 7., 8., 9., 10., 11.],
[21., 22., 23., 24., 25., 26.]])
Y: tensor([[ 7., 8., 9., 10., 11., 12.],
[22., 23., 24., 25., 26., 27.]]) 小结
-
时序数据采样方式包括随机采样和相邻采样。使用这两种方式的循环神经网络训练在实现上略有不同。
四、循环神经网络从零开始实现：
1、读取并加载数据
import time
import math
import numpy as np
import torch
from torch import nn, optim
import torch.nn.functional as F
import sys
sys.path.append("./Dive-into-DL-PyTorch/code/")
# print(os.getcwd())
# print(sys.path)
import d2lzh_pytorch as d2l
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# 加载数据集
sys.path.append("./Dive-into-DL-PyTorch/data")
(corpus_indices, char_to_idx, idx_to_char, vocab_size) = d2l.load_data_jay_lyrics()2、one-hot向量
为了将词表示成向量输入到神经网络，一个简单的办法是使用one-hot向量。假设词典中不同字符的数量为N（即词典大小vocab_size），每个字符已经同一个从0到N−1的连续整数值索引一一对应。如果一个字符的索引是整数i, 那么我们创建一个全0的长为N的向量，并将其位置为 i 的元素设成1。该向量就是对原字符的one-hot向量。下面分别展示了索引为0和2的one-hot向量，向量长度等于词典大小。
def one_hot(x, n_class, dtype=torch.float32):
# X shape: (batch), output shape: (batch, n_class)
x = x.long()
res = torch.zeros(x.shape[0], n_class, dtype=dtype, device=x.device)
res.scatter_(1, x.view(-1, 1), 1) # -1表示维数自动判断，行数计算，一列。关于scatter_的讲解：https://blog.csdn.net/t20134297/article/details/105755817
# 有时也可以采用label.unsequeeze(1)升维的方式来构造scatter_中第二个参数index。
return res
x = torch.tensor([0, 2])
one_hot(x, vocab_size)
# tensor([[1., 0., 0., ..., 0., 0., 0.],
# [0., 0., 1., ..., 0., 0., 0.]]) 我们每次采样的小批量的形状是(批量大小, 时间步数)。下面的函数将这样的小批量变换成数个可以输入进网络的形状为(批量大小, 词典大小)的矩阵，矩阵个数等于时间步数。也就是说，时间步 t 的输入为
，其中n为批量大小，d为输入个数，即one-hot向量长度（词典大小）。
为了使模型参数的计算只依赖一次迭代读取的小批量序列，我们可以在每次读取小批量前将隐藏状态从计算图中分离出来。
# 本函数已保存在d2lzh_pytorch包中方便以后使用
def to_onehot(X, n_class):
# X shape: (batch, seq_len), output: seq_len elements of (batch, n_class)
return [one_hot(X[:, i], n_class) for i in range(X.shape[1])]
X = torch.arange(10).view(2, 5)
inputs = to_onehot(X, vocab_size)
print(len(inputs), inputs[0].shape)
将vocab_size换成10来显示，结果如下：所以真正在进入神经网络之前，将批量数据以矩阵形式输入到网络。矩阵的最外层为时间步数5维，批量为2。每一个向量都是vocab_size长度的one-hot向量。
返回向量为：batchsize行， vocab_size列， 时间步t个的矩阵。初始X序列中的每一列，拿出来作为每个batch的索引，然后将每列数据作为索引one-hot编码。有多少列，有时间步数 t 列，作为时间步数 t 个输出。
[tensor([[1., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 1., 0., 0., 0., 0.]]),
tensor([[0., 1., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 1., 0., 0., 0.]]),
tensor([[0., 0., 1., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 1., 0., 0.]]),
tensor([[0., 0., 0., 1., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 1., 0.]]),
tensor([[0., 0., 0., 0., 1., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 1.]])]3、初始化模型参数：
初始化模型参数。隐藏单元个数num_hiddens是一个超参数。
num_inputs, num_hiddens, num_outputs = vocab_size, 256, vocab_size # 输入维度，隐藏维度，输出维度。
print('will use', device)
def get_params():
def _one(shape):
ts = torch.tensor(np.random.normal(0, 0.01, size=shape), device=device, dtype=torch.float32)
return torch.nn.Parameter(ts, requires_grad=True) # 参数初始化采用nn中的Parameter。
# 隐藏层参数
W_xh = _one((num_inputs, num_hiddens))
W_hh = _one((num_hiddens, num_hiddens))
b_h = torch.nn.Parameter(torch.zeros(num_hiddens, device=device, requires_grad=True))
# 输出层参数
W_hq = _one((num_hiddens, num_outputs))
b_q = torch.nn.Parameter(torch.zeros(num_outputs, device=device, requires_grad=True))
return nn.ParameterList([W_xh, W_hh, b_h, W_hq, b_q])
补充一张图：在从隐藏层到输出层，有一个权重矩阵为V，这也是代码中的：W_hq的来源。
4、定义模型
根据循环神经网络的计算表达式实现该模型。首先定义init_rnn_state函数来返回初始化的隐藏状态。它返回由一个形状为(批量大小，隐藏单元个数)的值为0的NDArray组成的元组。使用元组(python内存可视化)是为了更便于处理隐藏状态含有多个NDArray的情况。
def init_rnn_state(batch_size, num_hiddens, device):
return (torch.zeros((batch_size, num_hiddens), device=device), ) # 最后的一个逗号，表明只有一个元素的tuple下面的rnn函数定义了在一个时间步里如何计算隐藏状态和输出。这里的激活函数使用了tanh函数。当元素在实数域上均匀分布时，tanh函数值的均值为0。
def rnn(inputs, state, params):
# inputs和outputs皆为num_steps个形状为(batch_size, vocab_size)的矩阵
W_xh, W_hh, b_h, W_hq, b_q = params
H, = state
outputs = []
for X in inputs:
H = torch.tanh(torch.matmul(X, W_xh) + torch.matmul(H, W_hh) + b_h)
Y = torch.matmul(H, W_hq) + b_q
outputs.append(Y)
return outputs, (H,)
做个简单的测试来观察输出结果的个数(时间步数)， 以及第一个时间步的输出层输出的形状和隐藏状态的形状。
state = init_rnn_state(X.shape[0], num_hiddens, device)
inputs = to_onehot(X.to(device), vocab_size)
params = get_params()
outputs, state_new = rnn(inputs, state, params)
print(len(outputs), outputs[0].shape, state_new[0].shape) 5 torch.Size([2, 1027]) torch.Size([2, 256])5、定义预测函数
以下函数基于前缀prefix（含有数个字符的字符串）来预测接下来的num_chars个字符。这个函数稍显复杂，其中我们将函数：循环神经单元rnn：设置成了函数参数，这样在后面小节介绍其他循环神经网络时能重复使用这个函数。
# 本函数已保存在d2lzh_pytorch包中方便以后使用，参数num_chars为接下来要预测的字符个数。
def predict_rnn(prefix, num_chars, rnn, params, init_rnn_state,
num_hiddens, vocab_size, device, idx_to_char, char_to_idx):
state = init_rnn_state(1, num_hiddens, device)
# output列表为输出，将第一个输入即为初始输出。将字符转为序号。
output = [char_to_idx[prefix[0]]]
for t in range(num_chars + len(prefix) - 1):
# 将上一时间步的输出作为当前时间步的输入
X = to_onehot(torch.tensor([[output[-1]]], device=device), vocab_size)
# 计算输出和更新隐藏状态
(Y, state) = rnn(X, state, params)
# 下一个时间步的输入是prefix里的字符或者当前的最佳预测字符
if t < len(prefix) - 1:
output.append(char_to_idx[prefix[t + 1]])
else:
output.append(int(Y[0].argmax(dim=1).item()))
return ''.join([idx_to_char[i] for i in output]) # 序号最后转为字符。测试predict_rnn函数：根据前缀“分开”创作长度为10个字符（不考虑前缀长度）的一段歌词。
predict_rnn("分开",10, rnn, params, init_rnn_state, num_hiddens, vocab_size, device, idx_to_char, char_to_idx)6、裁剪梯度
循环神经网络中较容易出现梯度衰减或梯度爆炸。通过实践反向传播第六小节中解释原因。为了应对梯度爆炸，我们可以裁剪梯度（clip gradient）。 假设我们把所有模型参数梯度的元素拼接成一个向量
，并设裁剪的阈值为
。裁剪后的梯度
的L2范数不超过。
# 本函数已保存在d2lzh_pytorch包中方便以后使用
def grad_clipping(params, theta, device):
norm = torch.tensor([0.0], device=device)
for param in params:
norm += (param.grad.data ** 2).sum()
norm = norm.sqrt().item()
if norm > theta:
for param in params:
param.grad.data *= (theta / norm)7、困惑度
我们通常使用困惑度（perplexity）来评价语言模型的好坏。困惑度是对交叉熵损失函数做指数运算后得到的值。特别地，
-
最佳情况下，模型总是把标签类别的概率预测为1，此时困惑度为1；
-
最坏情况下，模型总是把标签类别的概率预测为0，此时困惑度为正无穷；
-
基线情况下，模型总是预测所有类别的概率都相同，此时困惑度为类别个数。
显然，任何一个有效模型的困惑度必须小于类别个数。在本例中，困惑度必须小于词典大小vocab_size。
猜测下一个字最合适的是哪个一字，可选字在词典中总共有vocab_size个。
8、定义模型训练函数
跟之前章节的模型训练函数相比，这里的模型训练函数有以下几点不同：
-
使用困惑度评价模型。
-
在迭代模型参数前裁剪梯度。
-
对时序数据采用不同采样方法将导致隐藏状态初始化的不同。
另外，考虑到后面将介绍的其他循环神经网络，为了更通用，这里的函数实现更长一些。
# 本函数已保存在d2lzh_pytorch包中方便以后使用
def train_and_predict_rnn(rnn, get_params, init_rnn_state, num_hiddens,
vocab_size, device, corpus_indices, idx_to_char,
char_to_idx, is_random_iter, num_epochs, num_steps,
lr, clipping_theta, batch_size, pred_period,
pred_len, prefixes):
if is_random_iter:
data_iter_fn = d2l.data_iter_random
else:
data_iter_fn = d2l.data_iter_consecutive
params = get_params()
# 损失函数采用交叉熵。
loss = nn.CrossEntropyLoss()
for epoch in range(num_epochs):
if not is_random_iter: # 如使用相邻采样，在epoch开始时初始化隐藏状态
state = init_rnn_state(batch_size, num_hiddens, device)
l_sum, n, start = 0.0, 0, time.time()
data_iter = data_iter_fn(corpus_indices, batch_size, num_steps, device)
for X, Y in data_iter:
if is_random_iter: # 如使用随机采样，在每个小批量更新前初始化隐藏状态
state = init_rnn_state(batch_size, num_hiddens, device)
else:
# 否则需要使用detach函数从计算图分离隐藏状态, 这是为了
# 使模型参数的梯度计算只依赖一次迭代读取的小批量序列(防止梯度计算开销太大)
for s in state:
s.detach_()
# detach和detach_都是在梯度计算时，阻断反向传播。
# 两者detach_()是对本身的更改，detach()则是生成了一个新的tensor。
inputs = to_onehot(X, vocab_size)
# outputs有num_steps个形状为(batch_size, vocab_size)的矩阵
(outputs, state) = rnn(inputs, state, params)
# 拼接之后形状为(num_steps * batch_size, vocab_size)
outputs = torch.cat(outputs, dim=0)
# Y的形状是(batch_size, num_steps)，转置后再变成长度为
# batch * num_steps 的向量，这样跟输出的行一一对应.
# transpose()交换矩阵的两个维度。转置。
y = torch.transpose(Y, 0, 1).contiguous().view(-1)
# 使用交叉熵损失计算平均分类误差
l = loss(outputs, y.long())
# 梯度清0
if params[0].grad is not None:
for param in params:
param.grad.data.zero_()
l.backward()
grad_clipping(params, clipping_theta, device) # 裁剪梯度
d2l.sgd(params, lr, 1) # 因为误差已经取过均值，梯度不用再做平均
l_sum += l.item() * y.shape[0]
n += y.shape[0]
if (epoch + 1) % pred_period == 0:
print('epoch %d, perplexity %f, time %.2f sec' % (
epoch + 1, math.exp(l_sum / n), time.time() - start))
for prefix in prefixes:
print(' -', predict_rnn(prefix, pred_len, rnn, params, init_rnn_state,
num_hiddens, vocab_size, device, idx_to_char, char_to_idx))9、训练模型并创作歌词
现在我们可以训练模型了。首先，设置模型超参数。我们将根据前缀“分开”和“不分开”分别创作长度为50个字符（不考虑前缀长度）的一段歌词。我们每过50个迭代周期便根据当前训练的模型创作一段歌词。
num_epochs, num_steps, batch_size, lr, clipping_theta = 250, 35, 32, 1e2, 1e-2
pred_period, pred_len, prefixes = 50, 50, ['分开', '不分开']采用随机采样训练模型并创作歌词。
train_and_predict_rnn(rnn, get_params, init_rnn_state, num_hiddens,
vocab_size, device, corpus_indices, idx_to_char,
char_to_idx, True, num_epochs, num_steps, lr,
clipping_theta, batch_size, pred_period, pred_len,
prefixes)采用相邻采样训练模型并创作歌词。
train_and_predict_rnn(rnn, get_params, init_rnn_state, num_hiddens,
vocab_size, device, corpus_indices, idx_to_char,
char_to_idx, False, num_epochs, num_steps, lr,
clipping_theta, batch_size, pred_period, pred_len,
prefixes)10、小结：
-
可以用基于字符级循环神经网络的语言模型来生成文本序列，例如创作歌词。
-
当训练循环神经网络时，为了应对梯度爆炸，可以裁剪梯度。
-
困惑度是对交叉熵损失函数做指数运算后得到的值。
五、循环神经网络的简洁实现：
使用PyTorch简洁实现RNN的语言模型。
1、加载数据：
import time
import math
import numpy as np
import torch
from torch import nn, optim
import torch.nn.functional as F
import sys
sys.path.append("./Dive-into-DL-PyTorch/code/")
# print(os.getcwd())
# print(sys.path)
import d2lzh_pytorch as d2l
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# 加载数据集
sys.path.append("./Dive-into-DL-PyTorch/data")
(corpus_indices, char_to_idx, idx_to_char, vocab_size) = d2l.load_data_jay_lyrics()2、定义模型：
# pytorch中nn模块提供了RNN的实现。构造一个单隐藏层
num_hiddens = 256
# rnn_layer = nn.LSTM(input_size=vocab_size, hidden_size=num_hiddens)
rnn_layer = nn.RNN(input_size=vocab_size, hidden_size=num_hiddens) rnn_layer的输入形状为(时间步数, 批量大小, 输入个数)。其中输入个数即one-hot向量长度（词典大小）。输出形状为(时间步数, 批量大小, 隐藏单元个数)，隐藏状态h的形状为(层数, 批量大小, 隐藏单元个数)。
num_steps = 35
batch_size = 2
state = None
X = torch.rand(num_steps, batch_size, vocab_size)
Y, state_new = rnn_layer(X, state)
print(Y.shape, len(state_new), state_new[0].shape)
接下来我们继承Module类来定义一个完整的循环神经网络。它首先将输入数据使用one-hot向量表示后输入到rnn_layer中，然后使用全连接输出层得到输出。输出个数等于词典大小vocab_size。
# 本类已保存在d2lzh_pytorch包中方便以后使用
class RNNModel(nn.Module):
def __init__(self, rnn_layer, vocab_size):
super(RNNModel, self).__init__()
self.rnn = rnn_layer
self.hidden_size = rnn_layer.hidden_size * (2 if rnn_layer.bidirectional else 1) # 是否双向。
self.vocab_size = vocab_size
self.dense = nn.Linear(self.hidden_size, vocab_size)
self.state = None
def forward(self, inputs, state): # inputs: (batch, seq_len)
# 获取one-hot向量表示
X = d2l.to_onehot(inputs, self.vocab_size) # X是个list
Y, self.state = self.rnn(torch.stack(X), state)
# 全连接层会首先将Y的形状变成(num_steps * batch_size, num_hiddens)，它的输出
# 形状为(num_steps * batch_size, vocab_size)
output = self.dense(Y.view(-1, Y.shape[-1]))
return output, self.state3、训练模型：
定义一个预测函数。
# 本函数已保存在d2lzh_pytorch包中方便以后使用
def predict_rnn_pytorch(prefix, num_chars, model, vocab_size, device, idx_to_char,
char_to_idx):
state = None
output = [char_to_idx[prefix[0]]] # output会记录prefix加上输出
for t in range(num_chars + len(prefix) - 1):
X = torch.tensor([output[-1]], device=device).view(1, 1)
if state is not None:
if isinstance(state, tuple): # LSTM, state:(h, c) lstm的state是元组。
state = (state[0].to(device), state[1].to(device))
else:
state = state.to(device)
(Y, state) = model(X, state)
if t < len(prefix) - 1:
output.append(char_to_idx[prefix[t + 1]])
else:
output.append(int(Y.argmax(dim=1).item()))
return ''.join([idx_to_char[i] for i in output])使用权重为随机值的模型来预测一次。
model = RNNModel(rnn_layer, vocab_size).to(device)
predict_rnn_pytorch('分开', 10, model, vocab_size, device, idx_to_char, char_to_idx)训练函数：相邻采样来读取数据。
# 本函数已保存在d2lzh_pytorch包中方便以后使用
def train_and_predict_rnn_pytorch(model, num_hiddens, vocab_size, device,
corpus_indices, idx_to_char, char_to_idx,
num_epochs, num_steps, lr, clipping_theta,
batch_size, pred_period, pred_len, prefixes):
loss = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=lr)
model.to(device)
state = None
for epoch in range(num_epochs):
l_sum, n, start = 0.0, 0, time.time()
data_iter = d2l.data_iter_consecutive(corpus_indices, batch_size, num_steps, device) # 相邻采样
for X, Y in data_iter:
if state is not None:
# 使用detach函数从计算图分离隐藏状态, 这是为了
# 使模型参数的梯度计算只依赖一次迭代读取的小批量序列(防止梯度计算开销太大)
if isinstance (state, tuple): # LSTM, state:(h, c)
state = (state[0].detach(), state[1].detach())
else:
state = state.detach()
(output, state) = model(X, state) # output: 形状为(num_steps * batch_size, vocab_size)
# Y的形状是(batch_size, num_steps)，转置后再变成长度为
# batch * num_steps 的向量，这样跟输出的行一一对应
y = torch.transpose(Y, 0, 1).contiguous().view(-1)
l = loss(output, y.long())
optimizer.zero_grad()
l.backward()
# 梯度裁剪
d2l.grad_clipping(model.parameters(), clipping_theta, device)
optimizer.step()
l_sum += l.item() * y.shape[0]
n += y.shape[0]
try:
perplexity = math.exp(l_sum / n)
except OverflowError:
perplexity = float('inf')
if (epoch + 1) % pred_period == 0:
print('epoch %d, perplexity %f, time %.2f sec' % (
epoch + 1, perplexity, time.time() - start))
for prefix in prefixes:
print(' -', predict_rnn_pytorch(
prefix, pred_len, model, vocab_size, device, idx_to_char,
char_to_idx))num_epochs, batch_size, lr, clipping_theta = 250, 32, 1e-3, 1e-2 # 注意这里的学习率设置
pred_period, pred_len, prefixes = 50, 50, ['分开', '不分开']
train_and_predict_rnn_pytorch(model, num_hiddens, vocab_size, device,
corpus_indices, idx_to_char, char_to_idx,
num_epochs, num_steps, lr, clipping_theta,
batch_size, pred_period, pred_len, prefixes)小结：
-
PyTorch的 nn模块提供了循环神经网络层的实现。
-
PyTorch的
nn.RNN实例在前向计算后会分别返回输出和隐藏状态。该前向计算并不涉及输出层计算。
六、通过时间反向传播：
1、定义模型
循环神经网络中梯度的计算和存储方法：通过时间反向传播（back-propagation through time）BPTT。
考虑一个无偏差项的循环神经网络，且激活函数为恒等映射（
）。时间步 t 的输入为单样本
，标签为
，那么隐藏状态
的计算表达式为：
t 时刻隐藏状态向量
t 时刻输出层输出变量
为 t 时刻隐藏层权重参数。
是上一时刻 t-1隐藏层权重参数。
为时间步 t 的输出层权重系数。
设时间步 t 的损失为
。时间步数为T的损失函数 L 定义为
。我们将L称为有关给定时间步的数据样本的目标函数。
2、模型计算图
可视化RNN中模型变量和参数在计算中的依赖关系，绘制模型计算图。例如：时间步3的隐藏状态
的计算依赖模型参数
、
、上一时间步隐藏状态
以及当前时间步输入
。
3、BPTT方法
训练模型通常需要模型参数的梯度：
、
、
。根据图中的依赖关系，我们按照箭头所指的反方向依次计算并存储梯度。
目标函数有关各时间步输出层变量的梯度 
: 计算：
目标函数有关模型参数
的梯度
： 如上图：
通过
依赖于。依链式法则：
同理：
小结：
当时间步数T较大或者时间步t较小时， 目标函数有关隐藏状态的梯度较容易出现衰减和爆炸。这会影响其他包含
项的梯度。
每一次迭代中，我们在依次计算完以上各个梯度后，会将他们存储起来，从而避免重复计算。
此外，反向传播中的梯度计算可能会依赖变量的当前值。它们正是通过正向传播计算出来的。
七、门控循环单元(GRU)：
当时间步数较大或者时间步较小时，循环神经网络的梯度较容易出现衰减或爆炸。裁剪梯度可以应对梯度爆炸，但无法解决梯度衰减的问题。通常由于这个原因，循环神经网络在实际中较难捕捉时间序列中时间步较大的依赖关系。
门控循环神经网络（gated recurrnet neural network）正是为了捕捉时间序列中时间步距离较大的依赖关系。通过可以学习的门来控制信息的流动。
两种门控循环神经网络结构：GRU和LSTM。
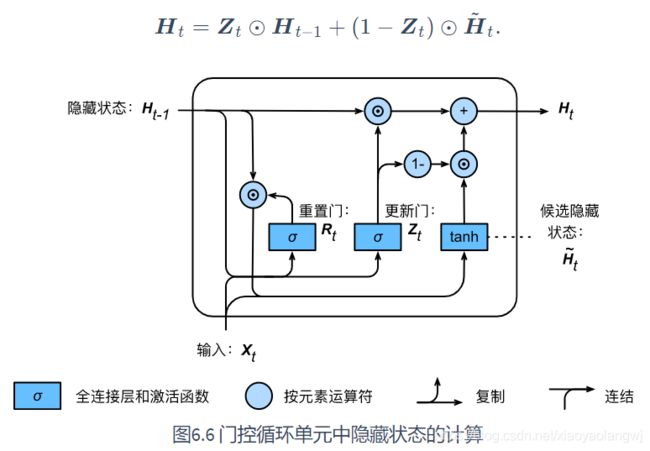
其中，门控循环单元（gated recurrent unit, GRU）是一种常见的门控循环神经网络。
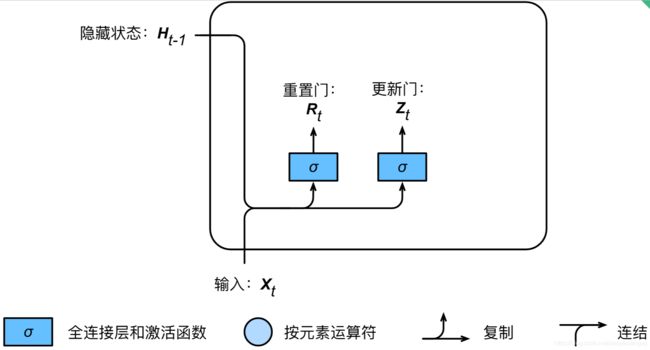
1、门控循环单元
引入了重置门（reset gate）和更新门（update gate）的概念。修改了循环神经网络中隐藏状态
的计算方式。
2、重置门和更新门
门控循环单元中重置门和更新门的计算
首先：门控循环单元中的重置门和更新门的输入均为当前时间步输入
与上一时间步隐藏状态
，输出由激活函数为sigmoid函数的全连接层计算得到。重置门和更新门计算如下：
sigmoid使重置门
和更新门
中的每个元素的值域[0, 1]。
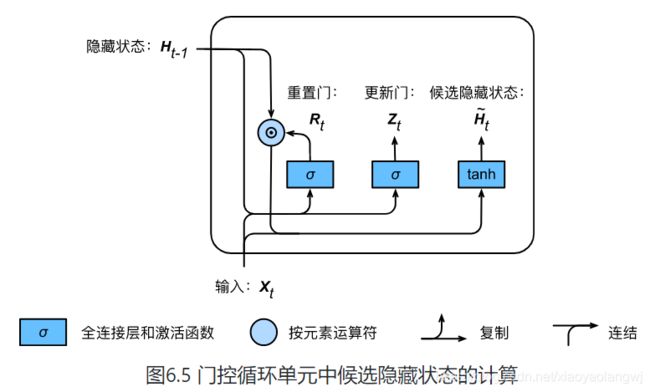
3、候选隐藏状态
接下来： 门控循环单元将计算候选隐藏状态来辅助稍后的隐藏状态计算。如上图，我们将当前时间步重置门的输出与上一时间步隐藏状态做按元素乘法
。
- 如果重置门中元素值接近0，那么意味着重置对应隐藏状态为0，即丢弃上一时间步的隐藏状态。
- 如果重置门中元素值接近1，那么表示保留上一时间步的隐藏状态。然后将按元素乘法的结果与当前时间步的输入连结，在通过含激活函数tanh函数的全连接层计算出候选隐藏状态，其所有元素的值域为[-1, 1]。
如上图中时间步t的候选隐藏状态计算为：
重置门控制了上一时间步的隐藏状态如何流入当前时间步的候选隐藏状态。而上一时间步的隐藏状态可能包含了时间序列截至上一时间步的全部历史信息。因此，重置门可以用来丢弃与预测无关的历史信息。
4、隐藏状态
最后：时间步t 的隐藏状态的计算使用当前时间步的更新门来对上一时间步的隐藏状态和当前时间步的候选隐藏状态
做组合。
更新门可以控制隐藏状态应该如何被包含当前时间步信息的候选隐藏状态所更新。更新规则。
- 假设更新门在时间步
到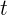
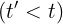之间一直近似1。那么时间步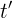到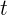之间的输入信息几乎没有流入时间步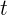的隐藏状态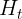。 - 实际上，这可以看作是较早时刻的隐藏状态一直通过时间保存并传递至当前时间步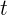。这个设计可以应对循环神经网络中的梯度衰减问题，并更好地捕捉时间序列中时间步距离较大的依赖关系。
重置门控制上一时间步隐藏状态如何流入当前时间步的候选隐藏状态。是否流入。
更新门控制隐藏状态如何被利用来更新当前时间步的隐藏状态。 更新规则
5、GRU小结
- 重置门有助于捕捉时间序列里短期的依赖关系；
- 更新门有助于捕捉时间序列里长期的依赖关系。
6、用GRU从零实现歌词预测
读取数据：
import time
import math
import numpy as np
import torch
from torch import nn, optim
import torch.nn.functional as F
import sys
sys.path.append("./Dive-into-DL-PyTorch/code/")
# print(os.getcwd())
# print(sys.path)
import d2lzh_pytorch as d2l
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# 加载数据集
sys.path.append("./Dive-into-DL-PyTorch/data")
(corpus_indices, char_to_idx, idx_to_char, vocab_size) = d2l.load_data_jay_lyrics()初始化模型参数：
num_inputs, num_hiddens, num_outputs = vocab_size, 256, vocab_size
print('will use', device)
def get_params():
def _one(shape):
ts = torch.tensor(np.random.normal(0, 0.01, size=shape), device=device, dtype=torch.float32)
return torch.nn.Parameter(ts, requires_grad=True)
def _three():
return (_one((num_inputs, num_hiddens)),
_one((num_hiddens, num_hiddens)),
torch.nn.Parameter(torch.zeros(num_hiddens, device=device, dtype=torch.float32), requires_grad=True))
W_xz, W_hz, b_z = _three() # 更新门参数
W_xr, W_hr, b_r = _three() # 重置门参数
W_xh, W_hh, b_h = _three() # 候选隐藏状态参数
# 输出层参数
W_hq = _one((num_hiddens, num_outputs))
b_q = torch.nn.Parameter(torch.zeros(num_outputs, device=device, dtype=torch.float32), requires_grad=True)
return nn.ParameterList([W_xz, W_hz, b_z, W_xr, W_hr, b_r, W_xh, W_hh, b_h, W_hq, b_q])定义模型：定义隐藏状态初始化函数init_gr_state。返回一个形状为（批量大小，隐藏单元个数）的值为0的Tensor组成的元组。
def init_gru_state(batch_size, num_hiddens, device):
return (torch.zeros((batch_size, num_hiddens), device=device), )根据门控循环单元的计算表达式定义模型。
def gru(inputs, state, params):
W_xz, W_hz, b_z, W_xr, W_hr, b_r, W_xh, W_hh, b_h, W_hq, b_q = params
H, = state
outputs = []
for X in inputs:
Z = torch.sigmoid(torch.matmul(X, W_xz) + torch.matmul(H, W_hz) + b_z)
R = torch.sigmoid(torch.matmul(X, W_xr) + torch.matmul(H, W_hr) + b_r)
H_tilda = torch.tanh(torch.matmul(X, W_xh) + torch.matmul(R * H, W_hh) + b_h)
H = Z * H + (1 - Z) * H_tilda
Y = torch.matmul(H, W_hq) + b_q
outputs.append(Y)
return outputs, (H,)训练模型并创作歌词
num_epochs, num_steps, batch_size, lr, clipping_theta = 160, 35, 32, 1e2, 1e-2
pred_period, pred_len, prefixes = 40, 50, ['分开', '不分开']d2l.train_and_predict_rnn(gru, get_params, init_gru_state, num_hiddens,
vocab_size, device, corpus_indices, idx_to_char,
char_to_idx, False, num_epochs, num_steps, lr,
clipping_theta, batch_size, pred_period, pred_len,
prefixes)7、PyTorch简洁实现
在PyTorch中我们直接调用nn模块中GRU类即可。
lr = 1e-2 # 注意调整学习率
gru_layer = nn.GRU(input_size=vocab_size, hidden_size=num_hiddens)
model = d2l.RNNModel(gru_layer, vocab_size).to(device)
d2l.train_and_predict_rnn_pytorch(model, num_hiddens, vocab_size, device,
corpus_indices, idx_to_char, char_to_idx,
num_epochs, num_steps, lr, clipping_theta,
batch_size, pred_period, pred_len, prefixes)小结：
- 门控循环神经网络可以更好地捕捉时间序列中时间步距离较大的依赖关系。
- 门控循环单元引入了门的概念，从而修改了循环神经网络中隐藏状态的计算方式。它包括重置门、更新门、候选隐藏状态和隐藏状态。
- 重置门有助于捕捉时间序列里短期的依赖关系。
- 更新门有助于捕捉时间序列里长期的依赖关系。
八、长短期记忆(LSTM)：
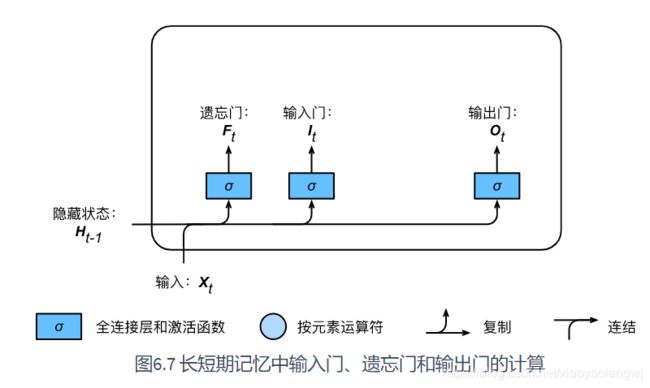
LSTM中引入了3个门，即输入门（input gate）、遗忘门（forget gate）和输出门（output gate）。同时还有与隐藏状态形状相同的记忆细胞（有些文献当成一种特殊的隐藏状态），用来记录额外的信息。
1、输入门、遗忘门、输出门
与门控循环单元GRU中的重置门和更新门一样。长短期记忆的门的输入均为当前时间步输入与上一时间步隐藏状态，输出由激活函数为sigmoid函数的全连接层计算得到。如此一来，这3个门元素的值域均为[0, 1]。
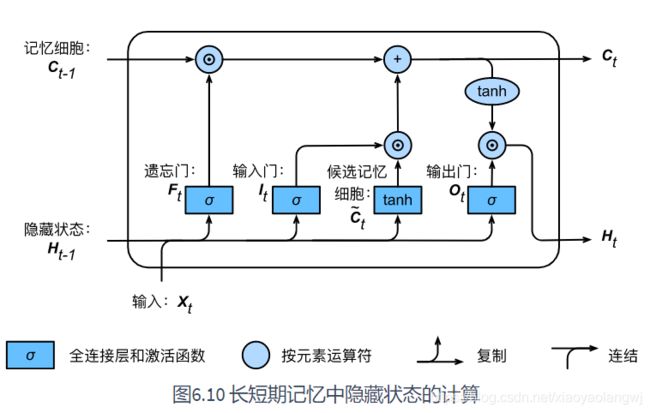
2、候选记忆细胞
接下来，长短期记忆需要计算候选记忆细胞
。它的计算与上面介绍的3个门类似，但使用了值域子[-1, 1]的tanh函数作为激活函数。
3、记忆细胞
通过元素值域在[0, 1]的输入门、遗忘门、输出门来控制隐藏状态中信息的流动，这一般也是通过使用按元素乘法来实现的。当前时间步记忆细胞
的计算组合了上一时间步记忆细胞和当前时间步候选记忆细胞的信息，并通过遗忘门和输入门来控制信息的流动。
遗忘门控制上一时间步的记忆细胞
中的信息是否传递到当前时间步。
输入门控制当前时间步的输入
如果遗忘门一致近似1且输入门一直近似0，过去的记忆细胞将一直通过时间保存并传递至当前时间步。这个设计可以应对循环神经网络中的梯度衰减问题，并更好地捕捉时间序列中时间步距离较大的依赖关系。
4、隐藏状态
有了记忆细胞，接下来我们还可以通过输出门来控制从记忆细胞到隐藏状态的信息流动：
这里的tanh函数确保隐藏状态元素值在-1到1之间。
- 当输出门近似1时，记忆细胞信息将传递到隐藏状态供输出层使用；
- 当输出门近似0时，记忆细胞信息只自己保留。
5、LSTM从零实现歌词预测
读取数据集
import time
import math
import numpy as np
import torch
from torch import nn, optim
import torch.nn.functional as F
import sys
sys.path.append("./Dive-into-DL-PyTorch/code/")
# print(os.getcwd())
# print(sys.path)
import d2lzh_pytorch as d2l
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# 加载数据集
sys.path.append("./Dive-into-DL-PyTorch/data")
(corpus_indices, char_to_idx, idx_to_char, vocab_size) = d2l.load_data_jay_lyrics()初始化模型参数
num_inputs, num_hiddens, num_outputs = vocab_size, 256, vocab_size
print('will use', device)
def get_params():
def _one(shape):
ts = torch.tensor(np.random.normal(0, 0.01, size=shape), device=device, dtype=torch.float32)
return torch.nn.Parameter(ts, requires_grad=True)
def _three():
return (_one((num_inputs, num_hiddens)),
_one((num_hiddens, num_hiddens)),
torch.nn.Parameter(torch.zeros(num_hiddens, device=device, dtype=torch.float32), requires_grad=True))
W_xi, W_hi, b_i = _three() # 输入门参数
W_xf, W_hf, b_f = _three() # 遗忘门参数
W_xo, W_ho, b_o = _three() # 输出门参数
W_xc, W_hc, b_c = _three() # 候选记忆细胞参数
# 输出层参数
W_hq = _one((num_hiddens, num_outputs))
b_q = torch.nn.Parameter(torch.zeros(num_outputs, device=device, dtype=torch.float32), requires_grad=True)
return nn.ParameterList([W_xi, W_hi, b_i, W_xf, W_hf, b_f, W_xo, W_ho, b_o, W_xc, W_hc, b_c, W_hq, b_q])定义模型：在初始化函数中，长短期记忆的隐藏状态需要返回额外的形状为(批量大小, 隐藏单元个数)的值为0的记忆细胞。
def init_lstm_state(batch_size, num_hiddens, device):
return (torch.zeros((batch_size, num_hiddens), device=device),
torch.zeros((batch_size, num_hiddens), device=device))只有隐藏状态会传递到输出层，而记忆细胞不参与输出层的计算。
def lstm(inputs, state, params):
[W_xi, W_hi, b_i, W_xf, W_hf, b_f, W_xo, W_ho, b_o, W_xc, W_hc, b_c, W_hq, b_q] = params
(H, C) = state
outputs = []
for X in inputs:
I = torch.sigmoid(torch.matmul(X, W_xi) + torch.matmul(H, W_hi) + b_i)
F = torch.sigmoid(torch.matmul(X, W_xf) + torch.matmul(H, W_hf) + b_f)
O = torch.sigmoid(torch.matmul(X, W_xo) + torch.matmul(H, W_ho) + b_o)
C_tilda = torch.tanh(torch.matmul(X, W_xc) + torch.matmul(H, W_hc) + b_c)
C = F * C + I * C_tilda
H = O * C.tanh()
Y = torch.matmul(H, W_hq) + b_q
outputs.append(Y)
return outputs, (H, C)训练模型并创作歌词
num_epochs, num_steps, batch_size, lr, clipping_theta = 160, 35, 32, 1e2, 1e-2
pred_period, pred_len, prefixes = 40, 50, ['分开', '不分开']d2l.train_and_predict_rnn(lstm, get_params, init_lstm_state, num_hiddens,
vocab_size, device, corpus_indices, idx_to_char,
char_to_idx, False, num_epochs, num_steps, lr,
clipping_theta, batch_size, pred_period, pred_len,
prefixes)6、PyTorch简洁实现
在Gluon中，我们直接调用rnn模块中的LSTM类。
lr = 1e-2 # 注意调整学习率
lstm_layer = nn.LSTM(input_size=vocab_size, hidden_size=num_hiddens)
model = d2l.RNNModel(lstm_layer, vocab_size)
d2l.train_and_predict_rnn_pytorch(model, num_hiddens, vocab_size, device,
corpus_indices, idx_to_char, char_to_idx,
num_epochs, num_steps, lr, clipping_theta,
batch_size, pred_period, pred_len, prefixes)小结：
- 长短期记忆的隐藏层输出包括隐藏状态和记忆细胞。只有隐藏状态会传递到输出层。
- 长短期记忆的输入门、遗忘门和输出门可以控制信息的流动。
- 长短期记忆可以应对循环神经网络中的梯度衰减问题，并更好地捕捉时间序列中时间步距离较大的依赖关系。
九、深度循环神经网络：
每个隐藏状态不断传递至当前层的下一时间步和当前时间步的下一层。
第1隐藏层的隐藏状态和之前的计算一样：
当
时，第
隐藏层的隐藏状态的表达式为：
最终，输出层的输出只需基于第L隐藏层的隐藏状态：
如果将隐藏状态的计算换成门控循环单元或者长短期记忆的计算，我们可以得到深度门控循环神经网络。
小结：
- 在深度循环神经网络中，隐藏状态的信息不断传递至当前层的下一时间步和当前时间步的下一层。
十、双向循环神经网络：
之前介绍的循环神经网络模型都是假设当前时间步是由前面的较早时间步的序列决定的，因此它们都将信息通过隐藏状态从前往后传递。有时候，当前时间步也可能由后面时间步决定。（上下文，前后文）
双向循环神经网络通过增加从后往前传递信息的隐藏层来更灵活地处理这类信息（上下文，前后文）。也就是说，未来时间步的隐藏状态（反向隐藏状态）与当前输入和过去隐藏状态来共同决定当前的输出。
我们分别计算正向隐藏状态和反向隐藏状态：
然后连结两个方向的隐藏状态
和
来得到隐藏状态
，并将其输入到输出层。计算输出
。
不同方向上的隐藏单元个数也可以不同。
小结：
-
双向循环神经网络在每个时间步的隐藏状态同时取决于该时间步之前和之后的子序列（包括当前时间步的输入）。