pytorch深度学习听课笔记
ps:个人学习笔记,视频链接https://www.bilibili.com/video/BV1Y7411d7Ys
参考链接https://blog.csdn.net/bit452/category_10569531.html
文章目录
- 相关知识点
- 线性模型
- 梯度下降
-
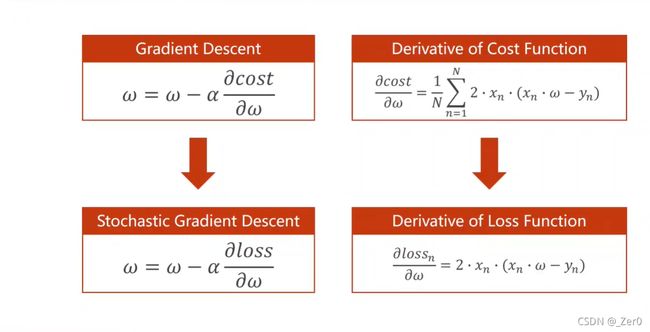
- 1.梯度下降
- 2.随机梯度下降
- 反向传播
-
- 1.两层神经网络示例
- 2.反向传播计算损失函数对权重偏导
- PyTorch框架实现线性回归
- 逻辑斯蒂回归(分类)
- 处理多维特征输入
- 加载数据集
- 多分类问题
- 卷积神经网络CNN
-
- 1.CNN基础
- 2.inception网络
相关知识点
损失函数(loss) 计算方法、 均方误差(方差mean square error) 计算方法。
注意区分loss是对一个样本,cost是对总体样本求平均值。
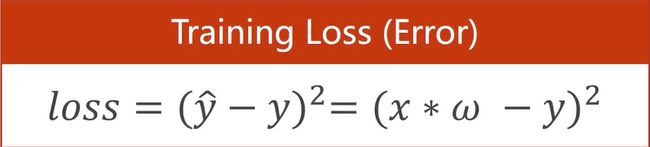

学习能力越强,有可能会把输入样本中噪声的规律也学到。
张量Tensor实际上就是一个多维数组,零位张量是标量,一维张量是向量,二位张量是矩阵…
线性模型
# 线性模型
import numpy as np
import matplotlib.pyplot as plt
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
# 计算y_pred
def forward(x):
return x*w
# 损失函数
def loss(x, y):
y_pred = forward(x)
return (y_pred - y) * (y_pred - y)
w_list = [] # 权重列表
mse_list = [] # 平均损失值mse列表
for w in np.arange(0.0, 4.1, 0.1):
print("w=%s" % w)
loss_sum = 0
for x_val, y_val in zip(x_data, y_data):
y_pred_val = forward(x_val)
loss_val = loss(x_val, y_val)
loss_sum += loss_val
print("\t", x_val, y_val, y_pred_val, loss_val)
print("MSE=%s" % (loss_sum/len(x_data)))
w_list.append(w)
mse_list.append(loss_sum/len(x_data))
plt.plot(w_list, mse_list)
plt.xlabel("w")
plt.ylabel("loss")
plt.show()
梯度下降
1.梯度下降
import matplotlib.pyplot as plt
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
# 初始权重,动态调整w
w = 1.0
# 画图
epoch_list = []
mse_list = []
# 计算y_pred
def forward(x):
return x*w
# 计算均方误差
def cost(xs, ys):
cost = 0
for x, y in zip(xs, ys):
y_pred = forward(x)
cost += (y_pred - y) ** 2
return cost / len(xs)
# 计算对权重的梯度
def gradient(xs, ys):
grad = 0
for x, y in zip(xs, ys):
grad += 2*x*(x*w-y)
return grad / len(xs)
for epoch in range(100):
cost_val = cost(x_data, y_data)
grad_val = gradient(x_data, y_data)
w -= 0.01 * grad_val
epoch_list.append(epoch)
mse_list.append(cost_val)
plt.plot(epoch_list, mse_list)
plt.xlabel("epoch")
plt.ylabel("loss")
plt.show()
2.随机梯度下降
import matplotlib.pyplot as plt
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
# 初始权重,动态调整w
w = 1.0
# 画图
epoch_list = []
mse_list = []
# 计算y_pred
def forward(x):
return x*w
# 计算单个样本损失函数
def loss(x, y):
y_pred = forward(x)
return (y_pred - y) ** 2
# 计算对权重的梯度
def gradient(x, y):
return 2*x*(x*w-y)
for epoch in range(100):
for x, y in zip(x_data, y_data):
grad = gradient(x, y)
w = w-0.01*grad
l = loss(x, y)
反向传播
1.两层神经网络示例
假设有一个两层神经网络如下左图,对应图如下右图


则可以化简为如下作图,对应图如下右图


然后每一层都需要加一个非线性变换,如下图,这个非线性变换就叫激活函数

在神经元中,输入的 inputs 通过加权,求和后,还被作用了一个函数,这个函数就是激活函数。引入激活函数是为了增加神经网络模型的非线性。没有激活函数的每层都相当于矩阵相乘。
2.反向传播计算损失函数对权重偏导
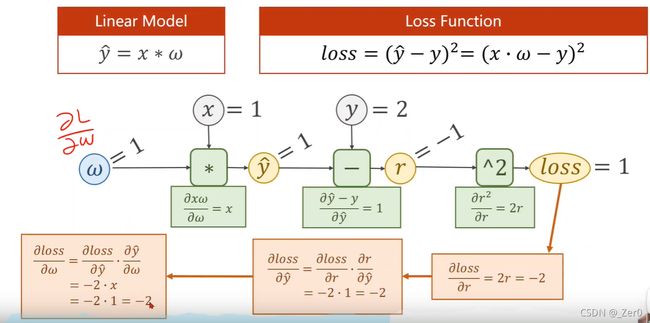
利用torch实现自动计算梯度的梯度下降算法
import torch
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
# w为权重
w = torch.tensor([1.0])
w.requires_grad = True # 需要计算梯度
# 计算
def forward(x):
return x * w #这里*被重载为tensor类型与tensor类型的乘法
# 损失函数
def loss(x, y):
y_pred = forward(x)
return (y_pred - y) ** 2
print("predict (before training) 4 -> %s", forward(4).item())
for epoch in range(100):
for x, y in zip(x_data, y_data):
l = loss(x, y) # l是一个张量
l.backward() # 自动计算这条链路上的所有梯度存到w中
print("grad: %s, %s, %s" % (x, y, w.grad.item()))
w.data = w.data - 0.01*w.grad.data
w.grad.data.zero_() # 梯度清零,防止下次计算累加
print("progress:%s, %s" % (epoch, l.item()))
print("predict (after training) 4 -> %s", forward(4).item())
# l.backward()会把计算图中所有需要梯度(grad)的地方都会求出来,然后把梯度都存在对应的待求的参数中
# tensor参与运算会构建计算图,但是取tensor中的data是不会构建计算图的
PyTorch框架实现线性回归
"""
1.准备数据集
2.设计模型计算y_hat
3.计算损失函数和优化器
4.前馈、反馈、更新
"""
import torch
x_data = torch.tensor([[1.0], [2.0], [3.0]])
y_data = torch.tensor([[2.0], [4.0], [6.0]])
class LinearModel(torch.nn.Module):
def __init__(self):
super(LinearModel, self).__init__()
# (1,1)是指输入x和输出y的特征维度,这里数据集中的x和y的特征都是1维的
# 该线性层需要学习的参数是w和b 获取w/b的方式分别是~linear.weight/linear.bias
self.linear = torch.nn.Linear(1,1)
def forward(self, x):
y_pred = self.linear(x)
return y_pred
model = LinearModel()
#计算损失函数
criterion = torch.nn.MSELoss(size_average=False)
# 优化器
# 梯度下降算法使用的是随机梯度下降,还是批量梯度下降,还是mini-batch梯度下降,
# 用的API都是 torch.optim.SGD
# lr为学习率
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
for epoch in range(100):
y_pred = model(x_data)
loss = criterion(y_pred, y_data)
print(epoch, loss.item())
optimizer.zero_grad() # 梯度归零
loss.backward() # 反向传播
optimizer.step() # 更新w和b
# 输出权重w和
print("w = %s" % model.linear.weight.item())
print("b = %s" % model.linear.bias.item())
# 测试4的结果
x_test = torch.Tensor([[4.0]])
y_test = model(x_test)
print("y_pred = %s" % y_test.data)
逻辑斯蒂回归(分类)
逻辑斯蒂回归相比于线性模型的区别是在线性模型的后面添加了一个非线性变换(也叫激活函数)
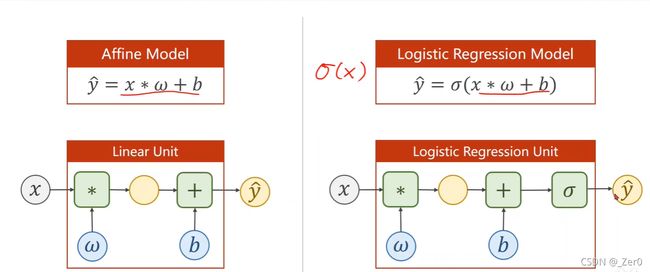
损失函数也发生了改变

损失函数计算示例,这里计算方法采用了交叉熵(CrossEntropy)的计算公式

BCELoss - Binary CrossEntropyLoss
BCELoss 是CrossEntropyLoss的一个特例,只用于二分类问题,而CrossEntropyLoss可以用于二分类,也可以用于多分类。
import torch
# 对于分类,这里假设场景为学习1小时和2小时不能通过考试,学习3小时能通过考试
# 1.0和2.0对应不能通过考试,3.0对应可以通过考试
x_data = torch.Tensor([[1.0], [2.0], [3.0]])
y_data = torch.Tensor([[0], [0], [1]])
# design model using class
class LogisticRegressionModel(torch.nn.Module):
def __init__(self):
super(LogisticRegressionModel, self).__init__()
self.linear = torch.nn.Linear(1,1)
def forward(self, x):
y_pred = torch.sigmoid(self.linear(x)) # 将结果映射到[0,1]
# sigmoid是一个非线性函数
return y_pred
model = LogisticRegressionModel()
# construct loss and optimizer
criterion = torch.nn.BCELoss(size_average = False)
optimizer = torch.optim.SGD(model.parameters(), lr = 0.01)
# training cycle forward, backward, update
for epoch in range(1000):
y_pred = model(x_data)
loss = criterion(y_pred, y_data)
print(epoch, loss.item())
optimizer.zero_grad()
loss.backward()
optimizer.step()
print('w = ', model.linear.weight.item())
print('b = ', model.linear.bias.item())
x_test = torch.Tensor([[4.0]])
y_test = model(x_test)
print('y_pred = ', y_test.data)
处理多维特征输入
以糖尿病数据集为例,输入为8维即8列特征值,计算入如下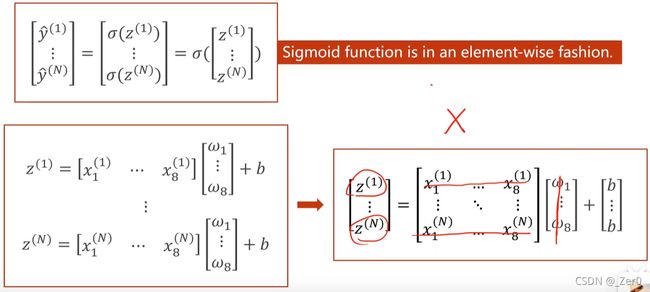
这里采用三层计算,通过矩阵的乘法特性,第一次运算将8维输入映射到6维,然后再映射到4维,最后映射到1维。(这可以通过乘不同维度的矩阵得到)
import numpy as np
import torch
import matplotlib.pyplot as plt
xy = np.loadtxt('C:/Users/jgc/Desktop/lab/diabetes.csv.gz', delimiter=',', dtype=np.float32)
x_data = torch.from_numpy(xy[:,:-1]) # 拿到前8列特征值
y_data = torch.from_numpy(xy[:,[-1]]) # [-1]拿到最后一列->一个矩阵
class Model(torch.nn.Module):
def __init__(self):
super(Model, self).__init__()
self.linear1 = torch.nn.Linear(8, 6) # 输入数据x的特征是8维(8个特征)
self.linear2 = torch.nn.Linear(6, 4) # 第二层转换
self.linear3 = torch.nn.Linear(4, 1) # 第三层
self.sigmoid = torch.nn.Sigmoid()
def forward(self, x):
x = self.sigmoid(self.linear1(x))
x = self.sigmoid(self.linear2(x))
x = self.sigmoid(self.linear3(x)) # y_hat
return x
model = Model()
criterion = torch.nn.BCELoss(reduction='mean') # 损失函数
optimizer = torch.optim.SGD(model.parameters(), lr=0.1) # 设置学习率
epoch_list = []
loss_list = []
for epoch in range(100):
y_pred = model(x_data)
loss = criterion(y_pred, y_data)
print(epoch, loss.item())
epoch_list.append(epoch)
loss_list.append(loss.item())
optimizer.zero_grad()
loss.backward()
optimizer.step()
plt.plot(epoch_list, loss_list)
plt.ylabel('loss')
plt.xlabel('epoch')
plt.show()
加载数据集
DataSet 是抽象类,不能实例化对象,主要是用于构造我们的数据集。
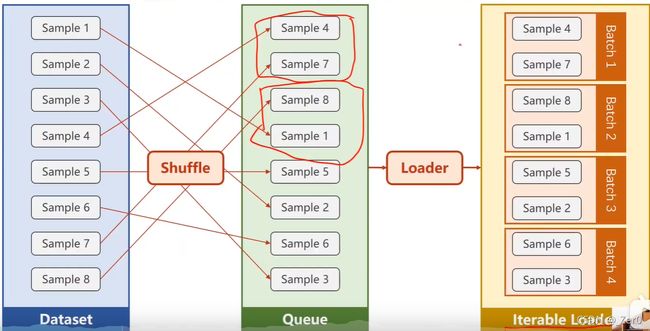
DataLoader 需要获取DataSet提供的索引[i]和len,加载数据,shuffle提高数据集的随机性,batch_size,能拿出Mini-Batch进行训练。
mini_batch 需要import DataSet和DataLoader
继承DataSet的类需要重写init(加载数据集),getitem(获取数据索引),len(获取数据总量)魔法函数。
DataLoader对数据集先打乱(shuffle),然后划分成mini_batch。
import torch
import numpy as np
from torch.utils.data import Dataset
from torch.utils.data import DataLoader
class DiabetesDataset(Dataset):
def __init__(self, filepath):
xy = np.loadtxt(filepath, delimiter=',', dtype=np.float32)
self.len = xy.shape[0] # shape(多少行,多少列)
self.x_data = torch.from_numpy(xy[:, :-1])
self.y_data = torch.from_numpy(xy[:, [-1]])
def __getitem__(self, index):
return self.x_data[index], self.y_data[index]
def __len__(self):
return self.len
dataset = DiabetesDataset('C:/Users/jgc/Desktop/lab/diabetes.csv')
train_loader = DataLoader(dataset=dataset, batch_size=32, shuffle=True, num_workers=0) #num_workers 多线程
class Model(torch.nn.Module):
def __init__(self):
super(Model, self).__init__()
self.linear1 = torch.nn.Linear(8, 6)
self.linear2 = torch.nn.Linear(6, 4)
self.linear3 = torch.nn.Linear(4, 1)
self.sigmoid = torch.nn.Sigmoid()
def forward(self, x):
x = self.sigmoid(self.linear1(x))
x = self.sigmoid(self.linear2(x))
x = self.sigmoid(self.linear3(x))
return x
model = Model()
criterion = torch.nn.BCELoss(reduction='mean')
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
if __name__ == '__main__':
for epoch in range(100):
for i, data in enumerate(train_loader, 0):
inputs, labels = data
y_pred = model(inputs)
loss = criterion(y_pred, labels)
print(epoch, i, loss.item())
optimizer.zero_grad()
loss.backward()
optimizer.step()
多分类问题
全连接神经网络
全连接层Fully Connected Layer
该层的每一个结点都与上一层的所有结点相连,用来把前边提取到的特征综合起来,把这样的线性层也叫全连接层。
每一层都是全连接层的网络叫全连接神经网络。
softmax两个作用:
1、如果在进行softmax前的input有负数,通过指数变换,得到正数。
2、所有分类的概率和为1。
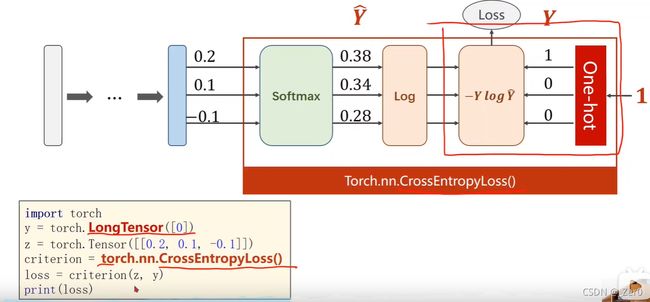
CrossEntropyLoss <==> LogSoftmax + NLLLoss。
即使用CrossEntropyLoss最后一层(线性层)是不需要做其他变化的;使用NLLLoss之前,需要对最后一层(线性层)先进行SoftMax处理,再进行log操作。
import torch
from torchvision import transforms
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.nn.functional as F
import torch.optim as optim
batch_size = 64
transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081,))]) # 归一化,均值和方差
train_dataset = datasets.MNIST(root='C:/Users/jgc/Desktop/lab/', train=True, download=True, transform=transform)
train_loader = DataLoader(train_dataset, shuffle=True, batch_size=batch_size) # 随机化+minibatch
test_dataset = datasets.MNIST(root='C:/Users/jgc/Desktop/lab/', train=False, download=True, transform=transform)
test_loader = DataLoader(test_dataset, shuffle=False, batch_size=batch_size)
class Net(torch.nn.Module):
def __init__(self):
super(Net, self).__init__()
self.l1 = torch.nn.Linear(784, 512)
self.l2 = torch.nn.Linear(512, 256)
self.l3 = torch.nn.Linear(256, 128)
self.l4 = torch.nn.Linear(128, 64)
self.l5 = torch.nn.Linear(64, 10)
def forward(self, x):
x = x.view(-1, 784) # -1是自动获取mini_batch
x = F.relu(self.l1(x))
x = F.relu(self.l2(x))
x = F.relu(self.l3(x))
x = F.relu(self.l4(x))
return self.l5(x) # 最后一层不做激活,不进行非线性变换
model = Net()
criterion = torch.nn.CrossEntropyLoss() #CrossEntropyLoss因该是根据target自动转的one-hot编码
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)
def train(epoch):
running_loss = 0.0
for batch_idx, data in enumerate(train_loader, 0):
# 获得一个批次的数据和标签
inputs, target = data
optimizer.zero_grad()
# 获得模型预测结果(64, 10)
outputs = model(inputs)
# 交叉熵代价函数outputs(64,10),target(64)
loss = criterion(outputs, target)
loss.backward()
optimizer.step()
running_loss += loss.item()
if batch_idx % 300 == 299:
print('[%d, %5d] loss: %.3f' % (epoch+1, batch_idx+1, running_loss/300))
running_loss = 0.0
def test():
correct = 0
total = 0
with torch.no_grad(): # 因为是test,不计算梯度
for data in test_loader:
images, labels = data
outputs = model(images)
_, predicted = torch.max(outputs.data, dim=1) # 列是第0个维度,行是第1个维度
total += labels.size(0)
correct += (predicted == labels).sum().item() # 张量之间的比较运算
print('accuracy on test set: %d %% ' % (100*correct/total))
if __name__ == '__main__':
for epoch in range(10):
train(epoch)
test()
卷积神经网络CNN
1.CNN基础
Convolutional Neural Network卷积神经网络
卷积神经网络流程

单通道卷积
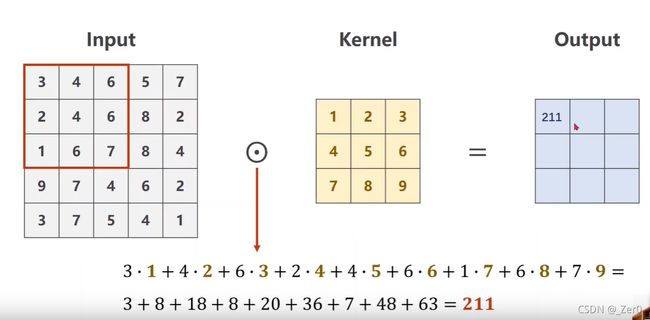
三通道卷积

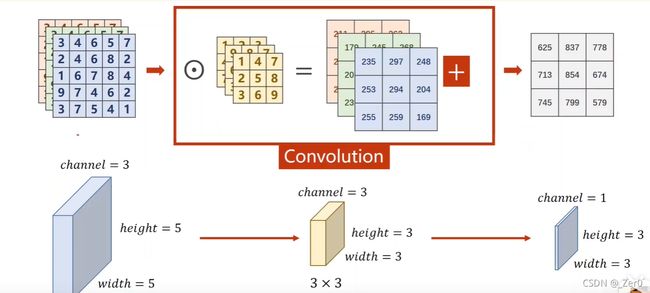
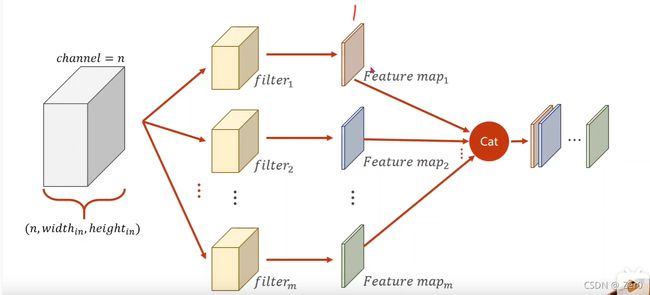
torch实现卷积示例
import torch
in_channels, out_channels = 5, 10
width, height = 100, 100
kernel_size = (3, 3)
batch_size = 1
input = torch.randn(batch_size, in_channels, width, height)
conv_layer = torch.nn.Conv2d(in_channels, out_channels, kernel_size = kernel_size)
output = conv_layer(input)
print(input.shape)
print(output.shape)
print(conv_layer.weight.shape)
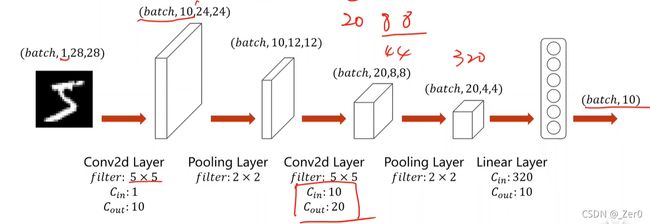
将上一节全连接神经网络实现的数字识别,转为使用卷积神经网络实现。

import torch
from torchvision import transforms
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.nn.functional as F
import torch.optim as optim
import matplotlib.pyplot as plt
batch_size = 64
transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081,))])
train_dataset = datasets.MNIST(root='C:/Users/jgc/Desktop/lab/', train=True, download=True, transform=transform)
train_loader = DataLoader(train_dataset, shuffle=True, batch_size=batch_size)
test_dataset = datasets.MNIST(root='C:/Users/jgc/Desktop/lab/', train=False, download=True, transform=transform)
test_loader = DataLoader(test_dataset, shuffle=False, batch_size=batch_size)
class Net(torch.nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = torch.nn.Conv2d(1, 10, kernel_size=5)
self.conv2 = torch.nn.Conv2d(10, 20, kernel_size=5)
self.pooling = torch.nn.MaxPool2d(2) # 2x2池化
self.fc = torch.nn.Linear(320, 10) # 全连接层(线性层)直接从320特征降到10个分类
def forward(self, x):
# flatten data from (n,1,28,28) to (n, 784)
batch_size = x.size(0)
x = F.relu(self.pooling(self.conv1(x)))
x = F.relu(self.pooling(self.conv2(x)))
x = x.view(batch_size, -1) # -1 此处自动算出的是320
x = self.fc(x)
return x
model = Net()
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model.to(device)
criterion = torch.nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)
def train(epoch):
running_loss = 0.0
for batch_idx, data in enumerate(train_loader, 0):
inputs, target = data
inputs, target = inputs.to(device), target.to(device)
optimizer.zero_grad()
outputs = model(inputs)
loss = criterion(outputs, target)
loss.backward()
optimizer.step()
running_loss += loss.item()
if batch_idx % 300 == 299:
print('[%d, %5d] loss: %.3f' % (epoch+1, batch_idx+1, running_loss/300))
running_loss = 0.0
def test():
correct = 0
total = 0
with torch.no_grad():
for data in test_loader:
images, labels = data
images, labels = images.to(device), labels.to(device)
outputs = model(images)
_, predicted = torch.max(outputs.data, dim=1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
print('accuracy on test set: %d %% ' % (100*correct/total))
return correct/total
if __name__ == '__main__':
epoch_list = []
acc_list = []
for epoch in range(10):
train(epoch)
acc = test()
epoch_list.append(epoch)
acc_list.append(acc)
plt.plot(epoch_list,acc_list)
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.show()
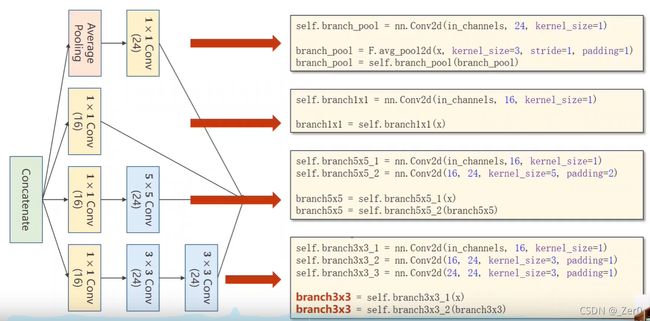
2.inception网络
import torch
import torch.nn as nn
from torchvision import transforms
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.nn.functional as F
import torch.optim as optim
batch_size = 64
transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081,))]) # 归一化,均值和方差
train_dataset = datasets.MNIST(root='C:/Users/jgc/Desktop/lab/', train=True, download=True, transform=transform)
train_loader = DataLoader(train_dataset, shuffle=True, batch_size=batch_size)
test_dataset = datasets.MNIST(root='C:/Users/jgc/Desktop/lab/', train=False, download=True, transform=transform)
test_loader = DataLoader(test_dataset, shuffle=False, batch_size=batch_size)
class InceptionA(nn.Module):
def __init__(self, in_channels):
super(InceptionA, self).__init__()
self.branch1x1 = nn.Conv2d(in_channels, 16, kernel_size=1)
self.branch5x5_1 = nn.Conv2d(in_channels, 16, kernel_size=1)
self.branch5x5_2 = nn.Conv2d(16, 24, kernel_size=5, padding=2)
self.branch3x3_1 = nn.Conv2d(in_channels, 16, kernel_size=1)
self.branch3x3_2 = nn.Conv2d(16, 24, kernel_size=3, padding=1)
self.branch3x3_3 = nn.Conv2d(24, 24, kernel_size=3, padding=1)
self.branch_pool = nn.Conv2d(in_channels, 24, kernel_size=1)
def forward(self, x):
branch1x1 = self.branch1x1(x)
branch5x5 = self.branch5x5_1(x)
branch5x5 = self.branch5x5_2(branch5x5)
branch3x3 = self.branch3x3_1(x)
branch3x3 = self.branch3x3_2(branch3x3)
branch3x3 = self.branch3x3_3(branch3x3)
branch_pool = F.avg_pool2d(x, kernel_size=3, stride=1, padding=1)
branch_pool = self.branch_pool(branch_pool)
outputs = [branch1x1, branch5x5, branch3x3, branch_pool]
return torch.cat(outputs, dim=1) # b,c,w,h c对应的是dim=1
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(1, 10, kernel_size=5)
self.conv2 = nn.Conv2d(88, 20, kernel_size=5) # 88 = 24x3 + 16
self.incep1 = InceptionA(in_channels=10) # 与conv1 中的10对应
self.incep2 = InceptionA(in_channels=20) # 与conv2 中的20对应
self.mp = nn.MaxPool2d(2)
self.fc = nn.Linear(1408, 10)
def forward(self, x):
in_size = x.size(0)
x = F.relu(self.mp(self.conv1(x)))
x = self.incep1(x)
x = F.relu(self.mp(self.conv2(x)))
x = self.incep2(x)
x = x.view(in_size, -1)
x = self.fc(x)
return x
model = Net()
criterion = torch.nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)
def train(epoch):
running_loss = 0.0
for batch_idx, data in enumerate(train_loader, 0):
inputs, target = data
optimizer.zero_grad()
outputs = model(inputs)
loss = criterion(outputs, target)
loss.backward()
optimizer.step()
running_loss += loss.item()
if batch_idx % 300 == 299:
print('[%d, %5d] loss: %.3f' % (epoch+1, batch_idx+1, running_loss/300))
running_loss = 0.0
def test():
correct = 0
total = 0
with torch.no_grad():
for data in test_loader:
images, labels = data
outputs = model(images)
_, predicted = torch.max(outputs.data, dim=1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
print('accuracy on test set: %d %% ' % (100*correct/total))
if __name__ == '__main__':
for epoch in range(10):
train(epoch)
test()
import torch
import torch.nn as nn
from torchvision import transforms
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.nn.functional as F
import torch.optim as optim
# prepare dataset
batch_size = 64
transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081,))]) # 归一化,均值和方差
train_dataset = datasets.MNIST(root='../dataset/mnist/', train=True, download=True, transform=transform)
train_loader = DataLoader(train_dataset, shuffle=True, batch_size=batch_size)
test_dataset = datasets.MNIST(root='../dataset/mnist/', train=False, download=True, transform=transform)
test_loader = DataLoader(test_dataset, shuffle=False, batch_size=batch_size)
# design model using class
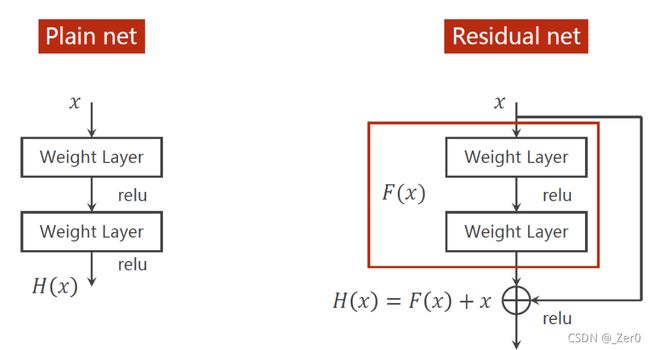
class ResidualBlock(nn.Module):
def __init__(self, channels):
super(ResidualBlock, self).__init__()
self.channels = channels
self.conv1 = nn.Conv2d(channels, channels, kernel_size=3, padding=1)
self.conv2 = nn.Conv2d(channels, channels, kernel_size=3, padding=1)
def forward(self, x):
y = F.relu(self.conv1(x))
y = self.conv2(y)
return F.relu(x + y)
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(1, 16, kernel_size=5)
self.conv2 = nn.Conv2d(16, 32, kernel_size=5) # 88 = 24x3 + 16
self.rblock1 = ResidualBlock(16)
self.rblock2 = ResidualBlock(32)
self.mp = nn.MaxPool2d(2)
self.fc = nn.Linear(512, 10) # 暂时不知道1408咋能自动出来的
def forward(self, x):
in_size = x.size(0)
x = self.mp(F.relu(self.conv1(x)))
x = self.rblock1(x)
x = self.mp(F.relu(self.conv2(x)))
x = self.rblock2(x)
x = x.view(in_size, -1)
x = self.fc(x)
return x
model = Net()
# construct loss and optimizer
criterion = torch.nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)
# training cycle forward, backward, update
def train(epoch):
running_loss = 0.0
for batch_idx, data in enumerate(train_loader, 0):
inputs, target = data
optimizer.zero_grad()
outputs = model(inputs)
loss = criterion(outputs, target)
loss.backward()
optimizer.step()
running_loss += loss.item()
if batch_idx % 300 == 299:
print('[%d, %5d] loss: %.3f' % (epoch+1, batch_idx+1, running_loss/300))
running_loss = 0.0
def test():
correct = 0
total = 0
with torch.no_grad():
for data in test_loader:
images, labels = data
outputs = model(images)
_, predicted = torch.max(outputs.data, dim=1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
print('accuracy on test set: %d %% ' % (100*correct/total))
if __name__ == '__main__':
for epoch in range(10):
train(epoch)
test()