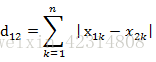《机器学习实战》—K-means聚类
机器学习实战—K-means聚类
K-means聚类算法原理及其相关概念
聚类是一种无监督的学习，它将相似的对象归到同一簇中，类似全自动分类。簇内的对象越相似，聚类的效果越好。K-均值聚类是每个类别簇都是采用簇中所含值的均值计算而成。聚类与分类的区别在于分类前目标已知，而聚类为无监督分类。
聚类把不相似的对象归到不同簇，相似度取决于选择的相似度计算方法：
1.欧式距离（edclidean distance）：
两个n维向量a（x11,x12,...,x1n）与b（x21,x22,...,x2n）的欧式距离
2.曼哈顿距离（Manhattan distance）：
两个n维向量a（x11,x12,...,x1n）与b（x21,x22,...,x2n）的曼哈顿距离
3.马氏距离（mahalanobis distance）：
马氏距离定义：有M个样本向量x1~xm，协方差矩阵记为S,均值记为u
其中样本向量X到u的距离为：
其中向量xi与xj之间的距离为：
另外还有切比雪夫距离，闵可夫斯基距离，标准欧式距离等等，在这里不多赘述。
K-means聚类算法
伪代码：创建k个点作为起始质心（经常是随机选择的）
当任意一个点的簇分配结果改变时：
对数据集中的每个点：
对每个质心：
计算质心与数据点之间的距离
将数据点分配到距离其最近的簇
对每一个簇，计算簇中所有的点的均值并将均值作为质心。
代码运行
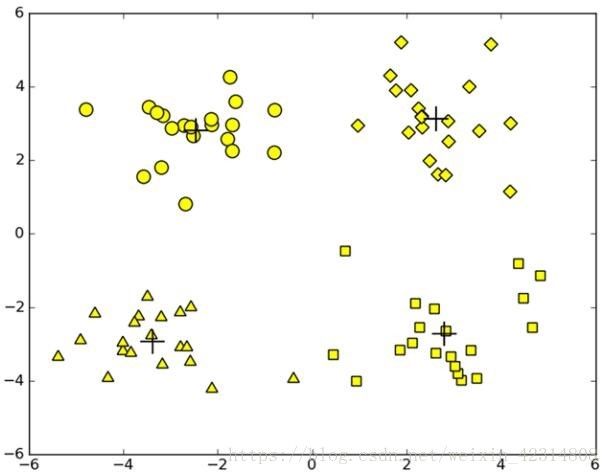
基本功能函数：数据加载函数，距离计算，初始化k个中心： K-均值聚类算法接收4个参数，两个必要参数为数据集和k的值，另外两个为距离计算函数和初始化函数（可修改）。算法采用计算质心-分配-重新计算质心反复迭代的方式，直到所有点的分配结果不再改变。设置flag为clusterChange=True。下图给出一个聚类结果示意图：
聚类算法的缺陷及如何提高聚类性能
缺陷： 1.簇的数目k是用户预先定义的参数，如何选择正确的k是很大的问题
2.k-均值算法收敛到局部最小值，而不是全局最小值提高聚类性能：由于执行随机初始化导致K-均值收敛效果较差
一种评价聚类效果的方法是SSE（Sum of Squared Error）误差平方和的方法，取平方的结果是使得远离中心的点变得更加突出。一种降低SSE的方法是增加簇的个数，即提高k值，但是违背了聚类的目标，聚类的目标是在不改变簇数目的前提下提高簇的质量。可选的改进的方法是对生成的簇进行后处理，将最大SSE值的簇划分成两个（K=2的K-均值算法），然后再进行相邻的簇合并。
具体方法有两种：1、合并最近的两个质心（合并使得SSE增幅最小的两个质心）
2、遍历簇合并两个然后计算SSE的值，找到使得SSE最小的情况。
二分K-均值算法
做法一：初始状态所有数据点属于一个大簇，之后每次选择一个簇切分成两个簇，这个切分满足使SSE值最大程度降低，直到簇数目达到k。
做法二：选择SSE最大的簇进行划分，直到簇数目达到用户指定的数目为之。
在代码中: 函数biKmeans是上面二分K-均值聚类算法的实现，首先创建clusterAssment储存数据集中每个点的分类结果和平方误差，用centList保存所有已经划分的簇，初始状态为整个数据集。while循环不停对簇进行划分，寻找使得SSE值最大程度减小的簇并更新，添加新的簇到centList中。
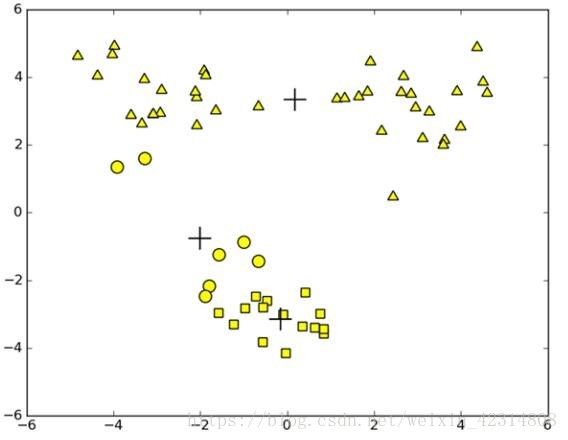
运行二分 K- 均值算法后的簇分配示意图，该算法总是产生较好的聚类效果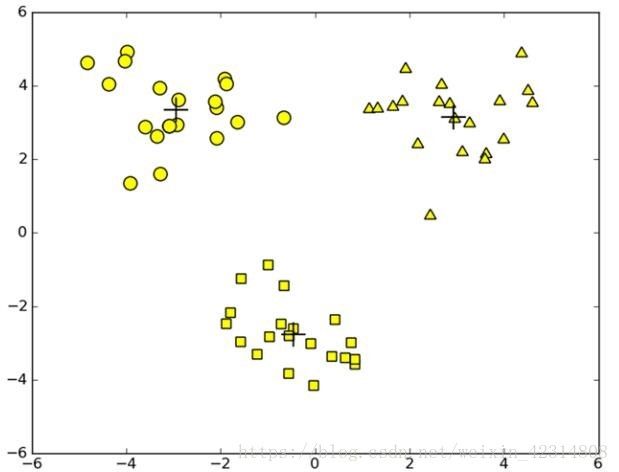
代码：
from numpy import *
#load data
def loadDataSet(fileName):
dataMat = []
fr = open(fileName)
for line in fr.readlines(): #for each line
curLine = line.strip().split('\t')
fltLine = list(map(float,curLine)) #这里和书中不同 和上一章一样修改
dataMat.append(fltLine)
return dataMat
#distance func
def distEclud(vecA,vecB):
return sqrt(sum(power(vecA - vecB, 2))) # la.norm(vecA-vecB) 向量AB的欧式距离
#init K points randomly
def randCent(dataSet, k):
n = shape(dataSet)[1]
centroids = mat(zeros((k,n)))#create centroid mat
for j in range(n):#create random cluster centers, within bounds of each dimension
minJ = min(dataSet[:,j])
rangeJ = float(max(dataSet[:,j]) - minJ)
centroids[:,j] = mat(minJ + rangeJ * random.rand(k,1))
return centroids
#K-均值算法:
def kMeans(dataSet,k,distMeas=distEclud,createCent=randCent):
#参数：dataset,num of cluster,distance func,initCen
m=shape(dataSet)[0]
clusterAssment=mat(zeros((m,2)))#store the result matrix,2 cols for index and error
centroids=createCent(dataSet,k)
clusterChanged=True
while clusterChanged:
clusterChanged=False
for i in range(m):#for every points
minDist = inf;minIndex = -1#init
for j in range(k):#for every k centers，find the nearest center
distJI=distMeas(centroids[j,:],dataSet[i,:])
if distJI', '<']
axprops = dict(xticks=[], yticks=[])
ax0=fig.add_axes(rect, label='ax0', **axprops)
imgP = plt.imread('Portland.png')#导入地图
ax0.imshow(imgP)
ax1=fig.add_axes(rect, label='ax1', frameon=False)
for i in range(numClust):
ptsInCurrCluster = datMat[nonzero(clustAssing[:,0].A==i)[0],:]
markerStyle = scatterMarkers[i % len(scatterMarkers)]
ax1.scatter(ptsInCurrCluster[:,0].flatten().A[0], ptsInCurrCluster[:,1].flatten().A[0], marker=markerStyle, s=90)
ax1.scatter(myCentroids[:,0].flatten().A[0], myCentroids[:,1].flatten().A[0], marker='+', s=300)
plt.show() 参考文献
【1】Peter Harrington, Machine Learning inAction[M] . US 2007