层次分析法原理讲解 python手搓实现-故事带入小白详解版
层次分析法
在参加研究生数学建模的时候用到了层次分析法,然后就写了个程序,比完赛了想着代码别浪费了拉出来写个教程,虽然这个算法很经典但是和往常一样我搜索了很多资料没有看起来比较舒服的,那就自己来吧。
问题构建-我应该选哪个人当女朋友
通俗的讲层次分析法就是当你面临选择困难的时候通过数学的方法最终为你确定最优的那个选项,其他的教程里举的都是旅游去哪的例子。
这回我们换个例子,假设你是个研究生,你叫龙傲天,目前有四个女生追你,对你都非常好,你也都有好感,但你不知道应该选谁在一起吗,一个是你青梅竹马的妹妹,一个是你本科就一直很崇拜你的目前已经工作了的学妹,一个是你目前研究生学校的一个学院的同届的同学,还有一个在参加学术会议的时候认识的其他学校的同研究领域的一届的姐姐。(以上纯属虚构)
她们的名字(设定)如下:
- 苏妤:青梅竹马的妹妹
- 季沫怡:本科就一直很崇拜你的目前已经工作了的学妹
- 叶之瑶:研究生学校的一个学院的同届的同学
- 莫筱竹:参加学术会议的时候认识的其他学校的同研究领域的一届的姐姐
你罗列了一下包括颜值在内的你会考虑的一些你觉得可能会影响你感情长久的因素
- A:颜值和身材
- B:性格
- C:在一起后相处的时间
- D:共同爱好或者话题
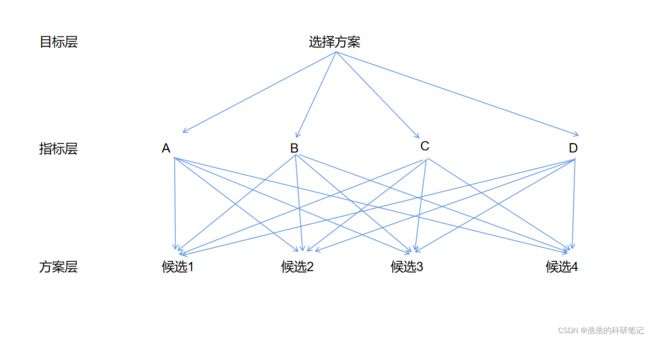
你的内心非常的焦虑,你决定使用科学的方法量化解决这个难题,你去学习了层次分析,首先你构建了问题的层次结构
指标层判断矩阵构建-在选择女朋友的过程中更看重那些方面
接下来你发现层次分析法需要你确认一个叫判断矩阵的东西,这个表会区别你对于指标层之间不同指标的重视程度,在填写这个判断矩阵之前你发现需要参照一个叫指标之间比较量化值规定表
指标层判断矩阵
| 因素i比较因素j | 量化值 |
|---|---|
| 同等重要 | 1 |
| 稍微重要 | 2 |
| 较强重要 | 5 |
| 强烈重要 | 7 |
| 极端重要 | 9 |
| 两相邻判断的中间值 | 2,4,6,8 |
| 倒数 | a i j = 1 a j i a_{ij}=\frac{1}{a_{ji}} aij=aji1 |
然后你根据你得理解构建了指标层的判断矩阵
| 指标层判断矩阵 | 颜值 | 性格 | 在一起之后的相处时间 | 共同爱好或者话题 |
|---|---|---|---|---|
| 颜值 | 1 | 1 2 \frac{1}{2} 21 | 1 2 \frac{1}{2} 21 | 1 4 \frac{1}{4} 41 |
| 性格 | 2 | 1 | 1 | 1 2 \frac{1}{2} 21 |
| 在一起之后的相处时间 | 2 | 1 | 1 | 1 2 \frac{1}{2} 21 |
| 共同爱好或者话题 | 4 | 2 | 2 | 1 |
你经过深思熟虑之后觉得性格和相处时间比颜值微微重要一些,所以你设置了 性格 颜值 = 2 \frac{性格}{颜值}=2 颜值性格=2, 相处时间 颜值 = 2 \frac{相处时间}{颜值}=2 颜值相处时间=2,性格好可以让两人减少很多矛盾,也不会无理取闹,在一起的相处时间长了可以避免异地的痛苦而,你认为有共同爱好或者话题是四个因素中最重要的比颜值来说在稍微重要一些也不说上较强重要所以你设置 共同话题 颜值 = 4 \frac{共同话题}{颜值}=4 颜值共同话题=4,有共同话题的话这样两个人即使不在一起也可以有话说有话聊,比如要是都喜欢看球的话那这就一个可以一直更新的话题,这样两个人的生活就不会枯燥,如果共同话题是论文,惹生气了还可以给发一篇SCI哄一哄吗哈哈哈,你这样想着。通过自己对两两因素之间重要程度的理解你填完了这个表。
你填好了之后发现事情没那么吗简单,需要判断一下,你填的矩阵能不能用,你发现这里有个专业性名词叫一致性检验,来判断你填的判断矩阵里有没有逻辑错误,比如下面这种出现了A比B重要,B比C重要,C又比A重要这种套圈的逻辑错误。
| 指标层判断矩阵 | A | B | C | D |
|---|---|---|---|---|
| A | 1 | 2 | 1 2 \frac{1}{2} 21 | 1 4 \frac{1}{4} 41 |
| B | 1 2 \frac{1}{2} 21 | 1 | 2 | 1 2 \frac{1}{2} 21 |
| C | 2 | 1 2 \frac{1}{2} 21 | 1 | 1 2 \frac{1}{2} 21 |
| D | 4 | 2 | 2 | 1 |
A B = 2 \frac{A}{B}=2 BA=2说明A比B重要
| 指标层判断矩阵 | A | B | C | D |
|---|---|---|---|---|
| A | 1 | 2 | 1 2 \frac{1}{2} 21 | 1 4 \frac{1}{4} 41 |
| B | 1 2 \frac{1}{2} 21 | 1 | 2 | 1 2 \frac{1}{2} 21 |
| C | 2 | 1 2 \frac{1}{2} 21 | 1 | 1 2 \frac{1}{2} 21 |
| D | 4 | 2 | 2 | 1 |
B C = 2 \frac{B}{C}=2 CB=2说明B比C重要
| 指标层判断矩阵 | A | B | C | D |
|---|---|---|---|---|
| A | 1 | 2 | 1 2 \frac{1}{2} 21 | 1 4 \frac{1}{4} 41 |
| B | 1 2 \frac{1}{2} 21 | 1 | 2 | 1 2 \frac{1}{2} 21 |
| C | 2 | 1 2 \frac{1}{2} 21 | 1 | 1 2 \frac{1}{2} 21 |
| D | 4 | 2 | 2 | 1 |
C A = 2 \frac{C}{A}=2 AC=2说明C比A重要
知道了判断矩阵不是填了就能直接用之后,你明白了一致性检验的必要性,然后你去看了一致性检验的步骤
第一步是要求判断矩阵的各层要素权重,你了解到有几何平均法还有算数平均法,你选择相对简单常用的算数平均法。
算数平均法第一步需要对每一列进行归一化,你发现这时候已经最好不用手算,你掏出了python准备一展身手
import numpy as np
#定义数组
index_layer = np.array([[1,1/2,1/2,1/4],[2,1,1,1/2],[2,1,1,1/2],[4,2,2,1]])
# 矩阵阶数
order = index_layer.shape[0]
# 归一化层输出
index_layer_nor = index_layer
# 按列归一化
for i in range(order):
#每一列除以这一列的和
index_layer_nor[:,i] = index_layer[:,i]/np.sum(index_layer[:,i])
print("归一化矩阵:\n",index_layer_nor,"\n")
归一化矩阵:
[[0.11111111 0.11111111 0.11111111 0.11111111]
[0.22222222 0.22222222 0.22222222 0.22222222]
[0.22222222 0.22222222 0.22222222 0.22222222]
[0.44444444 0.44444444 0.44444444 0.44444444]]
需要计算每一行的权重就是求每一行的平均值
index_layer_w = np.array([np.mean(i) for i in index_layer_nor]).reshape(order,1)
print("指标层权重:\n",index_layer_w,"\n")
指标层权重:
[[0.11111111]
[0.22222222]
[0.22222222]
[0.44444444]]
你看到了一个公式,说是求极大特征值,你想了想线性代数里的最大特征值是这么求的吗?不管了找对象要紧,就按它说的来吧,然后你继续往下看对应了一下变量,这里的 A A A其实就是最开始没有进行按列归一化的判断矩阵, w w w就是上面求出的指标层权重, N N N就是矩阵的阶数,比如这次指标层考虑了四个因素那 N = 4 N=4 N=4
λ m a x = ∑ i = 1 N [ A w ] i N w i \lambda_{max} = \sum\limits_{i=1}^N\frac{[Aw]_i}{Nw_i} λmax=i=1∑NNwi[Aw]i
为了求出下面这个最大特征值你先计算了 A w Aw Aw和 w w w
A w = [ 1 1 / 2 1 / 2 1 / 4 2 1 1 1 / 2 2 1 1 1 / 2 4 2 2 1 ] [ 1 / 9 2 / 9 2 / 9 4 / 9 ] = [ 4 / 9 8 / 9 8 / 9 16 / 9 ] Aw= \left[\begin{array}{c}1 & 1/2 & 1/2 & 1/4\\2 & 1 & 1& 1/2\\2 & 1 & 1& 1/2\\4 & 2 & 2 & 1\end{array}\right] \left[\begin{array}{c}1/9 \\ 2/9 \\ 2/9 \\ 4/9 \end{array}\right]=\left[\begin{array}{c}4/9 \\ 8/9 \\ 8/9 \\ 16/9 \end{array}\right] Aw=⎣ ⎡12241/21121/21121/41/21/21⎦ ⎤⎣ ⎡1/92/92/94/9⎦ ⎤=⎣ ⎡4/98/98/916/9⎦ ⎤
w = [ 1 / 9 2 / 9 2 / 9 4 / 9 ] w= \left[\begin{array}{c}1/9 \\ 2/9 \\ 2/9 \\ 4/9 \end{array}\right] w=⎣ ⎡1/92/92/94/9⎦ ⎤
之后你对 A w Aw Aw和 w w w两个向量按位做除法取平均之后,终于按照公式求出了最大特征值
lamb = np.sum(np.dot(index_layer,index_layer_w)/index_layer_w)/order
print("最大特征值:",lamb)
最大特征值: 4.0
接下来需要通过 λ m a x \lambda_{max} λmax求出一个叫 C I CI CI的东西然后通过 C I CI CI和再求出一个叫 C R CR CR的东西,然后如果这个叫 C R CR CR的东西小于0.1则就通过了一致性检验 C I CI CI的公式如下
C I = λ m a x − N N − 1 CI = \frac{\lambda_{max}-N}{N-1} CI=N−1λmax−N
你又看到了 C R CR CR的公式你发现这里的 R I RI RI又是什么东西,后来发现 R I RI RI有一个表对应不同的阶数有不同的固定值到时候只要查表就可以了。
C R = C I R I CR = \frac{CI}{RI} CR=RICI
RI = [0,0,0.52,0.89,1.12,1.36,1.41,1.46,1.49,1.52,1.54,1.56,1.58,1.59]
你整合了所有步骤对一个判断矩阵的全部处理就做完了你也得到了你的一个入门的例程
import numpy as np
# 一致性检验RI值
RI = [0,0,0.52,0.89,1.12,1.36,1.41,1.46,1.49,1.52,1.54,1.56,1.58,1.59]
index_layer = np.array([[1,1/2,1/2,1/4],[2,1,1,1/2],[2,1,1,1/2],[4,2,2,1]])
# 阶数
order = index_layer.shape[0]
# 归一化层输出话
index_layer_nor = np.array([x for x in index_layer])
# 按列归一化
for i in range(order):
index_layer_nor[:,i] = index_layer_nor[:,i]/np.sum(index_layer_nor[:,i])
print()
print("归一化矩阵:\n",index_layer_nor,"\n")
# 指标层权重
index_layer_w = np.array([np.mean(i) for i in index_layer_nor]).reshape(order,1)
print("指标层权重:\n",index_layer_w,"\n")
q = np.dot(index_layer,index_layer_w)
lamb = np.sum(np.dot(index_layer,index_layer_w)/index_layer_w)/order
print("最大特征值:",lamb)
# 一制化检验参数
CI = (lamb-order)/(order-1)
print("一制化检验参数CI:",CI)
CR = CI/(RI[order-1]+1e-10)
print("一制化检验参数CR:",CR)
if CR < 0.1:
print("一致性检验通过")
else:
print("一致性检验失败")
指标层判断矩阵计算结果
归一化矩阵:
[[0.11111111 0.11111111 0.11111111 0.11111111]
[0.22222222 0.22222222 0.22222222 0.22222222]
[0.22222222 0.22222222 0.22222222 0.22222222]
[0.44444444 0.44444444 0.44444444 0.44444444]]
指标层权重:
[[0.11111111]
[0.22222222]
[0.22222222]
[0.44444444]]
最大特征值: 4.0
一制化检验参数CI: 0.0
一制化检验参数CR: 0.0
一致性检验通过
你又尝试了一下如果换成之前内个逻辑有错误的矩阵一致性检验能不能通过呢,你将判断矩阵换成下面的样子,发现由于 C R CR CR的值大于0.1所以并没有通过一致性检验
index_layer = np.array([[1,2,1/2,1/4],[1/2,1,2,1/2],[2,1/2,1,1/2],[4,2,2,1]])
归一化矩阵:
[[0.13333333 0.36363636 0.09090909 0.11111111]
[0.06666667 0.18181818 0.36363636 0.22222222]
[0.26666667 0.09090909 0.18181818 0.22222222]
[0.53333333 0.36363636 0.36363636 0.44444444]]
指标层权重:
[[0.17474747]
[0.20858586]
[0.19040404]
[0.42626263]]
最大特征值: 4.455688050310713
一制化检验参数CI: 0.15189601677023776
一制化检验参数CR: 0.17066968174513572
一致性检验失败
制作相对于每一个指标的方案层的判断矩阵-在每一个指标方面哪一个佳人最优
谁最漂亮
接下你心如刀绞你发现使用这个算法的话必须对各位美女们的颜值做出评价,这时候你举一反三将量化表的重要程度变换成了你心中的颜值的美丽程度的。
| 因素i比较因素j | 量化值 |
|---|---|
| 同等漂亮 | 1 |
| 稍微漂亮 | 3 |
| 较强漂亮 | 5 |
| 强烈漂亮 | 7 |
| 极端漂亮 | 9 |
| 两相邻判断的中间值 | 2,4,6,8 |
| 倒数 | a i j = 1 a j i a_{ij}=\frac{1}{a_{ji}} aij=aji1 |
看着她们朋友圈的照片你认真的填了表,在你心里大概是 季沫怡,莫筱竹,叶之瑶,苏妤,你发现你还是比较喜欢大美女的类型。然后你用python求出了对应的权重并且审核通过了一致性检验。
方案层判断矩阵1
| 颜值 | 苏妤 | 季沫怡 | 叶之瑶 | 莫筱竹 |
|---|---|---|---|---|
| 苏妤 | 1 | 1 5 \frac{1}{5} 51 | 1 2 \frac{1}{2} 21 | 1 4 \frac{1}{4} 41 |
| 季沫怡 | 5 | 1 | 2 | 1 1 1 |
| 叶之瑶 | 2 | 1 2 \frac{1}{2} 21 | 1 | 1 2 \frac{1}{2} 21 |
| 莫筱竹 | 4 | 1 | 2 | 1 |
index_layer = np.array([[1,1/5,1/2,1/4],[5,1,2,1],[2,1/2,1,1/2],[4,1,2,1]])
方案层判断矩阵1结果
归一化矩阵:
[[0.08333333 0.07407407 0.09090909 0.09090909]
[0.41666667 0.37037037 0.36363636 0.36363636]
[0.16666667 0.18518519 0.18181818 0.18181818]
[0.33333333 0.37037037 0.36363636 0.36363636]]
权重:
[[0.0848064 ]
[0.37857744]
[0.17887205]
[0.35774411]]
最大特征值: 4.006232961694202
一制化检验参数CI: 0.0020776538980674295
一制化检验参数CR: 0.0023344425818359383
一致性检验通过
谁性格最好
你开始做第二个指标的判断矩阵就是判断每位美女的性格,你想用对性格的喜欢程度作为量化指标,你再次更改了量化比较表
| 因素i比较因素j | 量化值 |
|---|---|
| 同等喜欢 | 1 |
| 稍微喜欢 | 3 |
| 较强喜欢 | 5 |
| 强烈喜欢 | 7 |
| 极端喜欢 | 9 |
| 两相邻判断的中间值 | 2,4,6,8 |
| 倒数 | a i j = 1 a j i a_{ij}=\frac{1}{a_{ji}} aij=aji1 |
你回忆着和他们相处的点滴和她们聊天的过程你最终填了如下表格,苏妤是个好妹妹,温温柔柔的性格有点内向,能激起你得保护欲,季沫怡是个大美女,最求者众,对别人都是礼貌应对,只对你总会展露一些独有的笑容,叶之瑶是目前陪伴你时间最多的,也是最了解现阶段的你的,它能洞察你的情绪,性格也很开朗活泼,和她相处你总是不需要自己找话题,莫筱竹不怎么爱说话比较高冷也不太开玩笑,是一个外表清冷的憨憨美女,她主要是喜欢你和你在一起时你一直能逗她笑,回忆完毕你填了这个表。
方案层判断矩阵2
| 性格 | 苏妤 | 季沫怡 | 叶之瑶 | 莫筱竹 |
|---|---|---|---|---|
| 苏妤 | 1 | 2 | 1 2 \frac{1}{2} 21 | 4 |
| 季沫怡 | 1 2 \frac{1}{2} 21 | 1 | 1 3 \frac{1}{3} 31 | 2 |
| 叶之瑶 | 2 | 3 | 1 | 7 |
| 莫筱竹 | 1 4 \frac{1}{4} 41 | 1 2 \frac{1}{2} 21 | 1 7 \frac{1}{7} 71 | 1 |
index_layer = np.array([[1,2,1/2,4],[1/2,1,1/3,2],[2,3,1,7],[1/4,1/2,1/7,1]])
方案层判断矩阵2结果
归一化矩阵:
[[0.26666667 0.30769231 0.25301205 0.28571429]
[0.13333333 0.15384615 0.1686747 0.14285714]
[0.53333333 0.46153846 0.5060241 0.5 ]
[0.06666667 0.07692308 0.07228916 0.07142857]]
权重:
[[0.27827133]
[0.14967783]
[0.50022397]
[0.07182687]]
最大特征值: 4.007782809259693
一制化检验参数CI: 0.002594269753230923
一制化检验参数CR: 0.0029149098347634067
一致性检验通过
谁在一起之后能陪你的时间更久
你想着在一起了为了能长时间的互相陪伴,不想一处上就异地恋所以你考虑了一下每个人的实际情况,你第三次更改了量化比较表,来表示陪伴时间的多少。
| 因素i比较因素j | 量化值 |
|---|---|
| 同等多 | 1 |
| 稍微多 | 3 |
| 较强多 | 5 |
| 强烈多 | 7 |
| 极端多 | 9 |
| 两相邻判断的中间值 | 2,4,6,8 |
| 倒数 | a i j = 1 a j i a_{ij}=\frac{1}{a_{ji}} aij=aji1 |
你想了想目前每个人的状态,要是从即时角度来讲叶之瑶是是你目前在一个学校里的同学肯定是陪伴你时间最多的,但是你时长在外做项目其实也不怎么回学校,而且叶之瑶的家里人比较保守只希望女儿回到家乡的城市,但你的目标是在一个好一点的城市当大学老师,所以其实在一起之后能陪伴在一起的时间也不多,而苏妤也是一样目前她比你小几岁还在上大学,家里已经给安排好了工作,是在县城的一个国企,季沫怡目前在一线城市的一家科技公司做人事,父亲和母亲都是上市企业的高管,是因为本科的时候你给她做毕设都带她参加比赛,她很喜欢你的才华所以才追你,对她来说工作只是为了体验生活,莫筱竹和你一样希望和你一起当大学老师,如果在一起的话可以一起商量着去哪工作,这样在一个学校还能互相照应,想好了之后你认真填了下面的表格。
方案层判断矩阵3
| 相处之后的陪伴时间 | 苏妤 | 季沫怡 | 叶之瑶 | 莫筱竹 |
|---|---|---|---|---|
| 苏妤 | 1 | 1 3 \frac{1}{3} 31 | 1 | 1 4 \frac{1}{4} 41 |
| 季沫怡 | 3 | 1 | 2 | 1 |
| 叶之瑶 | 1 | 1/2 | 1 | 1 4 \frac{1}{4} 41 |
| 莫筱竹 | 4 | 1 | 4 | 1 |
index_layer = np.array([[1,1/3,1,1/4],[3,1,2,1],[1,1/2,1,1/4],[4,1,4,1]])
方案层判断矩阵3结果
归一化矩阵:
[[0.11111111 0.11764706 0.125 0.1 ]
[0.33333333 0.35294118 0.25 0.4 ]
[0.11111111 0.17647059 0.125 0.1 ]
[0.44444444 0.35294118 0.5 0.4 ]]
权重:
[[0.11343954]
[0.33406863]
[0.12814542]
[0.42434641]]
最大特征值: 4.045913260751297
一制化检验参数CI: 0.015304420250432216
一制化检验参数CR: 0.017195977807542267
一致性检验通过
谁的共同话题最多
你想着无论什么时候情侣之间有聊不完的话题才是最重要的,这样才可以一直维持住一定的新鲜感,不会感觉无聊,所以你想定量分析,和每个人之后能延展出的话题的多少,这次你直接使用了和相处时间一样的量化分析表。
| 因素i比较因素j | 量化值 |
|---|---|
| 同等多 | 1 |
| 稍微多 | 3 |
| 较强多 | 5 |
| 强烈多 | 7 |
| 极端多 | 9 |
| 两相邻判断的中间值 | 2,4,6,8 |
| 倒数 | a i j = 1 a j i a_{ij}=\frac{1}{a_{ji}} aij=aji1 |
你想了想和每一个聊天的时候大概都在聊什么,和苏妤聊天的时候,其实一般都是分享她吃的好吃的,给你讲讲校园生活中的琐事,偶尔会回忆回忆童年,你一直都是一个倾听的角色,季沫怡一般会给你发一些她国内国外旅游的照片,比如在巴塞罗那街头,背手拿着一个她最喜欢的米色包包,穿着一件黑色的连衣裙,迈着跳脱似的步伐边走边打量周边的街道,再或者坐在塞纳河边一手从侧面缕着发丝,一边看着河对岸城市的绚丽的夜景的倒影,一次发来好多张问你哪张最好看,哈哈哈,你这个大直男每次都只会说哪张都好看,然后发一个可爱的猫猫的表情。叶之瑶你想了想一般你们会聊一些学校同学之间的八卦或者故事,每次组会之前都会到你这找一下安慰,相对来说四个人里你会更愿意找她倾诉一下遇到的不开心,可能是因为她性格比较开朗,被这种温柔阳光的性格感染,总是能帮助你缓和心态。莫筱竹虽然感觉有点冰冰的,但是你们每次出去开会都会找对方吃个饭逛一逛,因为研究方向的相近,每次沟通都能产生新的点子,所以你们很期待每次见面交流学术,而且她竟然是一个稀有的女球迷,是因为他父亲小时候带她去英国旅游带她现场看了一场英超,她便喜欢上了足球场的氛围,有一次在烧烤店吃烧烤,屏幕正好放着曼联的比赛,你说:哎这马奎尔上抢之后身后留下的空当没人来补位,这曼联后卫思想不统一啊,这被单刀被进能怪别人吗,回过头发现她很认真的盯着屏幕,缓缓的说道,嗯这曼联三条线的距离实在太远,中场一拿球对面高位逼抢很凶,球传不到C罗脚下,进攻确实组织不起来,腾哈格下半场应该做出调整了,我一脸震惊从那之后我们晚上经常会一起连麦边看球中场的时候就聊聊最近有没有新点子,看她这吗喜欢C罗过生日还送了她一件C罗正版的7号球衣,她收到之后穿着拍了好几张照片,还说要送你一篇论文哈哈哈,回忆完了你低头看着屏幕填完了最后一个判断矩阵。
方案层判断矩阵4
| 共同话题 | 苏妤 | 季沫怡 | 叶之瑶 | 莫筱竹 |
|---|---|---|---|---|
| 苏妤 | 1 | 1 | 1 | 1 4 \frac{1}{4} 41 |
| 季沫怡 | 1 | 1 | 1 | 1 4 \frac{1}{4} 41 |
| 叶之瑶 | 1 | 1 | 1 | 1 4 \frac{1}{4} 41 |
| 莫筱竹 | 4 | 4 | 4 | 1 |
index_layer = np.array([[1,1,1,1/4],[1,1,1,1/4],[1,1,1,1/4],[4,4,4,1]])
方案层判断矩阵4结果
归一化矩阵:
[[0.14285714 0.14285714 0.14285714 0.14285714]
[0.14285714 0.14285714 0.14285714 0.14285714]
[0.14285714 0.14285714 0.14285714 0.14285714]
[0.57142857 0.57142857 0.57142857 0.57142857]]
指标层权重:
[[0.14285714]
[0.14285714]
[0.14285714]
[0.57142857]]
最大特征值: 4.0
一制化检验参数CI: 0.0
一制化检验参数CR: 0.0
一致性检验通过
最终决策准备
你呆呆的望着屏幕,接下来开始要做最终的决策了,你整合了一下你所计算到的权重
w 指标层 = [ 0.11111111 0.22222222 0.22222222 0.44444444 ] w 颜值 = [ 0.0848064 0.37857744 0.17887205 0.35774411 ] w 性格 = [ 0.27827133 0.14967783 0.50022397 0.07182687 ] w 陪伴时间 = [ 0.11343954 0.33406863 0.12814542 0.42434641 ] w 共同话题 = [ 0.14285714 0.14285714 0.14285714 0.57142857 ] w_{指标层}= \left[\begin{array}{c}0.11111111 \\ 0.22222222 \\ 0.22222222 \\ 0.44444444 \end{array}\right] w_{颜值}= \left[\begin{array}{c}0.0848064 \\ 0.37857744\\ 0.17887205 \\ 0.35774411 \end{array}\right] w_{性格}= \left[\begin{array}{c}0.27827133 \\ 0.14967783 \\ 0.50022397 \\ 0.07182687 \end{array}\right] w_{陪伴时间}= \left[\begin{array}{c}0.11343954\\ 0.33406863 \\ 0.12814542 \\ 0.42434641\end{array}\right] w_{共同话题}= \left[\begin{array}{c}0.14285714 \\ 0.14285714 \\ 0.14285714 \\ 0.57142857 \end{array}\right] w指标层=⎣ ⎡0.111111110.222222220.222222220.44444444⎦ ⎤w颜值=⎣ ⎡0.08480640.378577440.178872050.35774411⎦ ⎤w性格=⎣ ⎡0.278271330.149677830.500223970.07182687⎦ ⎤w陪伴时间=⎣ ⎡0.113439540.334068630.128145420.42434641⎦ ⎤w共同话题=⎣ ⎡0.142857140.142857140.142857140.57142857⎦ ⎤
接下来需要得到每个人每一项的权重值格式如下
w 名称 = [ 颜值权重 性格权重 陪伴时间权重 共同话题权重 ] w_{名称}= \left[\begin{array}{c}颜值权重 \\ 性格权重 \\ 陪伴时间权重 \\ 共同话题权重 \end{array}\right] w名称=⎣ ⎡颜值权重性格权重陪伴时间权重共同话题权重⎦ ⎤
具体如下
w 苏妤 = [ w 颜值 [ 0 ] w 性格 [ 0 ] w 陪伴时间 [ 0 ] w 共同话题 [ 0 ] ] w 季沫怡 = [ w 颜值 [ 1 ] w 性格 [ 1 ] w 陪伴时间 [ 1 ] w 共同话题 [ 1 ] ] w 叶之瑶 = [ w 颜值 [ 2 ] w 性格 [ 2 ] w 陪伴时间 [ 2 ] w 共同话题 [ 2 ] ] w 莫筱竹 = [ w 颜值 [ 3 ] w 性格 [ 3 ] w 陪伴时间 [ 3 ] w 共同话题 [ 3 ] ] w_{苏妤}= \left[\begin{array}{c}w_{颜值}[0] \\ w_{性格}[0] \\ w_{陪伴时间}[0] \\ w_{共同话题}[0] \end{array}\right] w_{季沫怡}= \left[\begin{array}{c}w_{颜值}[1] \\ w_{性格}[1] \\ w_{陪伴时间}[1] \\ w_{共同话题}[1] \end{array}\right] w_{叶之瑶}= \left[\begin{array}{c}w_{颜值}[2] \\ w_{性格}[2] \\ w_{陪伴时间}[2] \\ w_{共同话题}[2] \end{array}\right] w_{莫筱竹}= \left[\begin{array}{c}w_{颜值}[3] \\ w_{性格}[3] \\ w_{陪伴时间}[3] \\ w_{共同话题}[3] \end{array}\right] w苏妤=⎣ ⎡w颜值[0]w性格[0]w陪伴时间[0]w共同话题[0]⎦ ⎤w季沫怡=⎣ ⎡w颜值[1]w性格[1]w陪伴时间[1]w共同话题[1]⎦ ⎤w叶之瑶=⎣ ⎡w颜值[2]w性格[2]w陪伴时间[2]w共同话题[2]⎦ ⎤w莫筱竹=⎣ ⎡w颜值[3]w性格[3]w陪伴时间[3]w共同话题[3]⎦ ⎤
w 苏妤 = [ 0.0848064 0.27827133 0.11343954 0.14285714 ] w 季沫怡 = [ 0.37857744 0.14967783 0.33406863 0.14285714 ] w 叶之瑶 = [ 0.17887205 0.50022397 0.12814542 0.14285714 ] w 莫筱竹 = [ 0.35774411 0.07182687 0.42434641 0.57142857 ] w_{苏妤}= \left[\begin{array}{c}0.0848064 \\ 0.27827133 \\ 0.11343954 \\ 0.14285714 \end{array}\right] w_{季沫怡}= \left[\begin{array}{c}0.37857744\\ 0.14967783 \\ 0.33406863\\ 0.14285714\end{array}\right] w_{叶之瑶}= \left[\begin{array}{c}0.17887205 \\ 0.50022397 \\ 0.12814542 \\ 0.14285714 \end{array}\right] w_{莫筱竹}= \left[\begin{array}{c}0.35774411 \\ 0.07182687 \\ 0.42434641 \\ 0.57142857\end{array}\right] w苏妤=⎣ ⎡0.08480640.278271330.113439540.14285714⎦ ⎤w季沫怡=⎣ ⎡0.378577440.149677830.334068630.14285714⎦ ⎤w叶之瑶=⎣ ⎡0.178872050.500223970.128145420.14285714⎦ ⎤w莫筱竹=⎣ ⎡0.357744110.071826870.424346410.57142857⎦ ⎤
最后算出的得分的公式
w 最终权重 = w 指标层 T × [ w 苏妤 w 季沫怡 w 叶之瑶 w 莫筱竹 ] = [ 苏妤 季沫怡 叶之瑶 莫筱竹 ] w_{最终权重}=w_{指标层}^T×\left[\begin{array}{c}w_{苏妤} & w_{季沫怡} & w_{叶之瑶} & w_{莫筱竹} \end{array}\right]=\left[\begin{array}{c}苏妤 & 季沫怡 & 叶之瑶 & 莫筱竹 \end{array}\right] w最终权重=w指标层T×[w苏妤w季沫怡w叶之瑶w莫筱竹]=[苏妤季沫怡叶之瑶莫筱竹]
苏妤 = w 指标层 [ 0 ] × w 颜值 [ 0 ] + w 指标层 [ 1 ] × w 性格 [ 0 ] + w 指标层 [ 2 ] × w 陪伴时间 [ 0 ] + w 指标层 [ 3 ] × w 共同话题 [ 0 ] 季沫怡 = w 指标层 [ 0 ] × w 颜值 [ 1 ] + w 指标层 [ 1 ] × w 性格 [ 1 ] + w 指标层 [ 2 ] × w 陪伴时间 [ 1 ] + w 指标层 [ 3 ] × w 共同话题 [ 1 ] 叶之瑶 = w 指标层 [ 0 ] × w 颜值 [ 2 ] + w 指标层 [ 1 ] × w 性格 [ 2 ] + w 指标层 [ 2 ] × w 陪伴时间 [ 2 ] + w 指标层 [ 3 ] × w 共同话题 [ 2 ] 莫筱竹 = w 指标层 [ 0 ] × w 颜值 [ 3 ] + w 指标层 [ 1 ] × w 性格 [ 3 ] + w 指标层 [ 2 ] × w 陪伴时间 [ 3 ] + w 指标层 [ 3 ] × w 共同话题 [ 3 ] 苏妤=w_{指标层}[0]×w_{颜值}[0]+w_{指标层}[1]×w_{性格}[0]+w_{指标层}[2]×w_{陪伴时间}[0]+w_{指标层}[3]×w_{共同话题}[0] \\ 季沫怡=w_{指标层}[0]×w_{颜值}[1]+w_{指标层}[1]×w_{性格}[1]+w_{指标层}[2]×w_{陪伴时间}[1]+w_{指标层}[3]×w_{共同话题}[1]\\ 叶之瑶=w_{指标层}[0]×w_{颜值}[2]+w_{指标层}[1]×w_{性格}[2]+w_{指标层}[2]×w_{陪伴时间}[2]+w_{指标层}[3]×w_{共同话题}[2]\\ 莫筱竹=w_{指标层}[0]×w_{颜值}[3]+w_{指标层}[1]×w_{性格}[3]+w_{指标层}[2]×w_{陪伴时间}[3]+w_{指标层}[3]×w_{共同话题}[3]\\ 苏妤=w指标层[0]×w颜值[0]+w指标层[1]×w性格[0]+w指标层[2]×w陪伴时间[0]+w指标层[3]×w共同话题[0]季沫怡=w指标层[0]×w颜值[1]+w指标层[1]×w性格[1]+w指标层[2]×w陪伴时间[1]+w指标层[3]×w共同话题[1]叶之瑶=w指标层[0]×w颜值[2]+w指标层[1]×w性格[2]+w指标层[2]×w陪伴时间[2]+w指标层[3]×w共同话题[2]莫筱竹=w指标层[0]×w颜值[3]+w指标层[1]×w性格[3]+w指标层[2]×w陪伴时间[3]+w指标层[3]×w共同话题[3]
在输出最终的结果之前还有一个步骤就是判断算法整体是否可以通过一致性检验,就是还要算一个整体的CR,算法整体的CR值就是对应指标层的权重乘以对应指标判断矩阵计算权重时产生的CR值然后求和,判断这个数值是不是小于0.1如果小于则通过了整体的一致性检验。
C R f i n a l = w 指标层 T [ 颜值判断矩阵 C R 性格判断矩阵 C R 陪伴时间判断矩阵 C R 共同话题判断矩阵 C R ] CR_{final}= w_{指标层}^T \left[\begin{array}{c}颜值判断矩阵CR \\ 性格判断矩阵CR \\ 陪伴时间判断矩阵CR \\ 共同话题判断矩阵CR \end{array}\right] CRfinal=w指标层T⎣ ⎡颜值判断矩阵CR性格判断矩阵CR陪伴时间判断矩阵CR共同话题判断矩阵CR⎦ ⎤
然后你埋头苦干终于写出了代码
完整代码
import numpy as np
import matplotlib.pyplot as plt
RI = [0,0,0.52,0.89,1.12,1.36,1.41,1.46,1.49,1.52,1.54,1.56,1.58,1.59]
#解决自己的问题需要自己更改A,B,index_layer,scheme_layer
#温馨提示:更改时一定要注意矩阵维度
#指标层名称(可更改)
A =["颜值","性格","陪伴时间","共同话题"]
#方案层名称(可更改)
B =["苏妤","季沫怡","叶之瑶","莫筱竹"]
#指标层判断矩阵(可更改)
index_layer = np.array([[1,1/2,1/2,1/4],[2,1,1,1/2],[2,1,1,1/2],[4,2,2,1]])
# index_layer = np.random.random((len(A),len(A)))
# 方案层权重(可更改)
scheme_layer = np.array([
[[1,1/5,1/2,1/4],[5,1,2,1],[2,1/2,1,1/2],[4,1,2,1]],
[[1,2,1/2,4],[1/2,1,1/3,2],[2,3,1,7],[1/4,1/2,1/7,1]],
[[1,1/3,1,1/4],[3,1,2,1],[1,1/2,1,1/4],[4,1,4,1]],
[[1,1,1,1/4],[1,1,1,1/4],[1,1,1,1/4],[4,4,4,1]]
])
def get_w(layer):
# 初始化保存案列归一化结果的矩阵
layer_nor = np.array([x for x in layer])
# 获取判断矩阵阶数(计算用)
order = layer.shape[0]
# 算数平均法案列归一化
for i in range(order):
layer_nor[:,i] = layer[:, i] / np.sum(layer[:, i])
# 判断矩阵的权重
layer_w = np.array([np.mean(i) for i in layer_nor]).reshape(order,1)
# 判断矩阵的最大特征值(用于一致性检验)
lamb = np.sum(np.dot(layer, layer_w) / layer_w) / order
# 一制化检验参数
CI = (lamb-order)/(order-1)
CR = CI/(RI[order-1]+1e-10)
#如果矩阵报错则停止运行输出错误的参数和矩阵
if CR > 0.1:
print("失败矩阵:\n",layer,"\n")
print("一制性检验参数CI:",CI)
print("一制性 检验参数CR:",CR)
print(" 一致性检验失败:CR < 0.1")
raise Exception("一致性检验失败")
return CR,layer_w
#计算指标层的权重CR值
index_layer_ci,index_layer_w = get_w(index_layer)
scheme_layer_w = []
# 存储计算出的最终的方案层的权重
final_w = []
# 存储计算scheme_layer中每一个判断矩阵的的权重时产生的CR值用于最后计算整体的CR值
CR = []
# 计算scheme_layer中判断矩阵的权重和CR值
for id,layer in enumerate(scheme_layer):
[cr,w] = get_w(layer)
CR.append(cr)
scheme_layer_w.append(w.reshape(-1))
print(f"{A[id]}权重:{round(index_layer_w.reshape(-1)[id],4)}")
print("其判断矩阵对应的方案权重为:")
for i in range(len(B)):
print(f"{B[i]}:{round(w[i][0],4)}",end='\t')
print()
print()
print()
# 计算最终的结果的权重结果
final_w = np.array([np.dot(index_layer_w.T,i) for i in np.array(scheme_layer_w).T]).reshape(-1)
# 计算最终整体的CR值
final_CR = np.sum(index_layer_w * np.array(CR))
# 判断算法整体的CR值是否能通过一致性检验
if final_CR > 0.1:
raise Exception("最终一致性检验失败")
# 获取最终矩阵的最大值权重的索引
final_choose = np.argmax(final_w)
# 打印方案层的权重
print("方案权重:")
for i in range(len(B)):
print(f"{B[i]}:",round(final_w.reshape(-1)[i],4),end="\t")
print()
print()
# 输出最终方案
print("最终方案:",B[final_choose])
print("最终方案权重:",round(final_w[final_choose],4))
# 这两行代码解决 plt 中文显示的问题
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 绘图部分
bar_width = 0.1 # 条形宽度
index_male = np.arange(len(B)) # 条形图的横坐标
# 柱状图颜色
color = ['r','g','b','y','m']
for i in range(len(A)):
plt.bar(index_male+bar_width*i, height=scheme_layer_w[i], width=bar_width, color=color[i], label=A[i])
plt.bar(index_male+bar_width*(len(A)), height=final_w, width=bar_width, color='m', label='最终权重')
plt.legend() # 显示图例
plt.xticks(index_male+bar_width*(len(A)//2), B)
plt.ylabel('权重大小') # 纵坐标轴标题
plt.title('权重柱状图') # 图形标题
plt.show()
结果!-最终选了谁
颜值权重:0.1111
其判断矩阵对应的方案权重为:
苏妤:0.0848 季沫怡:0.3786 叶之瑶:0.1789 莫筱竹:0.3577
性格权重:0.2222
其判断矩阵对应的方案权重为:
苏妤:0.2783 季沫怡:0.1497 叶之瑶:0.5002 莫筱竹:0.0718
陪伴时间权重:0.2222
其判断矩阵对应的方案权重为:
苏妤:0.1134 季沫怡:0.3341 叶之瑶:0.1281 莫筱竹:0.4243
共同话题权重:0.4444
其判断矩阵对应的方案权重为:
苏妤:0.1429 季沫怡:0.1429 叶之瑶:0.1429 莫筱竹:0.5714
方案权重:
苏妤: 0.16 季沫怡: 0.2131 叶之瑶: 0.223 莫筱竹: 0.404
最终方案: 莫筱竹
最终方案权重: 0.404
结束
十年后…
英国爱丁堡大学 信息学院 教授办公室
咚咚咚…
「Is Professor Long in ?」(龙教授在嘛)
你放下鼠标眼睛从订票网站上移开
「进来吧,莫莫,一听就知道你是」
门被打开,一个穿着白色小羽绒服小女孩向你飞奔而来
「爸爸!」
「哎!诺诺怎么也来了」
莫筱竹关上门了之后,在诺诺后面走了过来
「还在忙呢,诺诺说想你了,说爸爸怎么放假还不回家,所以我们两个决定来突击你」
「哈哈哈,诺诺来」
你双手从胳膊下面托住跑过来的诺诺一下给她托举了起来
「小心点!别给诺诺磕到」
「这次爸爸不但买了迪士尼的门票,还买了今年在温布利的欧冠决赛的VIP包厢,带你和妈妈好好玩一玩」
「莫莫,明天就是圣诞节了,也是我们在一起的纪念日,有没有什么愿望」
「你先给诺诺放下来」
「哦对对对」
你缓缓的放下了诺诺,诺诺下地之后满办公室跑呀跑
莫莫很不放心急忙说
「小心点别摔着」
诺诺忽然转头盯着你的沙发,眼睛里像有两个小星星,一下就冲了过去在上面打起了滚
莫莫看到诺诺自己玩的正开心,转头对你说
「老夫老妻了,今年我有个问题想问你,十年前那天,之前我怎么暗示你都装傻,为什么忽然内晚上就想开了」
你没有直接回答面带微笑的抓起了椅子上的衣服穿上,边穿边笑着说
「这得感谢一个叫萨蒂人,他让我明白你才是我最想要在一起的人」
莫莫表现出似懂非懂的样子很是可爱
「哈哈哈,别想了先,走吧叫上诺诺回家收拾行李准备明天出去玩」
「走啦诺诺回家了」
你去沙发上准备抱起诺诺
此时莫莫看着你的背影,嘴里小声气鼓鼓的说了一句
「哼!为什么我的颜值分不是最高的,性格分还给我倒数第一」
你的注意力都在诺诺身上并没有听清,边抱起诺诺,边回头问
「怎么啦莫莫」
莫莫看着抱起诺诺的你,看你们父女二人,表情变得很温柔
「没事,没事,走吧,一会儿你开车!听见没!」
「好嘞!媳妇」