matlab & yalmip在微电网优化调度中的应用(一)
matlab & yalmip在微电网优化调度中的应用(一)——基础模型
- 基础模型
-
- 组成
- 目的
- 建模
- 编程实现
-
- 1.决策变量
- 2.约束条件
- 3.目标函数
- 4.优化设置
- 5.结果可视化
- 结果与分析
- 写在最后
写在前面
这是“matlab & yalmip在微电网优化调度中的应用”系列的第一篇,本系列致力于解决微电网优化调度问题,而这一篇文章将建立解决问题的整体思路和最基础的模型。
基础模型叙述略微冗长,可以直接跳至“编程实现”。
基础模型
组成
简单模型中含有一个微型燃气轮机 G G G、一个蓄电池 B a Ba Ba、一个太阳能光伏 P V PV PV 、4一个风力发电机组 W W W、一个负荷 L L L共5个组分。另外,这个微电网通过 P C C PCC PCC与外部大电网相连。
目的
微电网优化调度的目的是:通过调整各组分的出力以及充分利用可再生能源,满足微电网的用电需求,并使得微电网运行成本最小。
建模
1.出于简化的目的, G G G、 B a Ba Ba为可调度能源,作为新能源的 P V PV PV, W W W和负荷 L L L一样不可调度,可以视为“负的”负荷。
2.【决策变量】除了对 G G G、 B a Ba Ba的调度,还可以通过向外部大电网购电,售电维持电网稳定运行,而我们的决策变量也就是:G的出力 P G P_G PG,Ba的出力 P B a P_{Ba} PBa,外部联络功率 P g r i d P_{grid} Pgrid。
3.【约束条件】首先我们的微电网必须满足功率平衡约束,也就是电源出力等于负荷的用电需要。
考虑到实际情况, G G G有出力的上下限,且有爬坡限制; B a Ba Ba也有出力限制,且出力的下限可以为复数,因为 B a Ba Ba是可以充电的;外部联络功率也一样。
4.【目标函数】 G G G、 B a Ba Ba运行产生成本,向外部电网购电售电也会产生成本,(风电和光伏产生成本固定,可以不计入用于优化的目标函数)这些成本的和就是目标函数——总成本。
编程实现
1.决策变量
我们想得到 24 h 24h 24h内的最优调度方案,故构建 3 × 24 3\times24 3×24的优化变量矩阵:
T = 24;
P = sdpvar(3,T);
2.约束条件
1.功率平衡约束
每个小时内,所有电源的出力加上与电网交换的功率等于负荷功率:
P G + P B a + P g r i d = P L − P W − P P V P_G+P_{Ba}+P_{grid}=P_L-P_{W}-P_{PV} PG+PBa+Pgrid=PL−PW−PPV
Constraints = [];
for i = 1:T
Constraints = [Constraints; sum(P(:,i)) == PL(i) - PPV(i) - PW(i)];
end
2.出力限制和爬坡限制
G G G出力 P G P_G PG、 B a Ba Ba出力 P B a P_{Ba} PBa以及电网交换功率均有上下限:
P G m i n ≤ P G ≤ P G m a x P B a m i n ≤ P B a ≤ P B a m a x P_G^{min}\leq P_G\leq P_G^{max} \\ P_{Ba}^{min}\leq P_{Ba} \leq P_{Ba}^{max} PGmin≤PG≤PGmaxPBamin≤PBa≤PBamax
PG_min = 0;PG_max = 50;
PBa_min = -60;PBa_max = 60;
Pgrid_max = 200;Pgrid_min = -200;
for i = 1:T
Constraints = [Constraints; PG_min <= P(1,i) <= PG_max;
PBa_min <= P(2,i) <= PBa_max;
Pgrid_min <= P(3,i) <= Pgrid_max];
end
G G G的出力 P G P_G PG还有爬坡限制:
Δ P G m i n ≤ Δ P G ≤ Δ P G m a x \Delta P_G^{min} \leq \Delta P_G \leq \Delta P_G^{max} ΔPGmin≤ΔPG≤ΔPGmax
dPG_min = -12;dPG_max = 12;
for i = 2:T
Constraints = [Constraints; dPG_min <= (P(1,i)-P(1,i-1)) <= dPG_max];
end
3.目标函数
为了简化问题,只考虑 G G G, B a Ba Ba出力和电网交换带来的成本,且认为成本是线性的:
f c = ∑ t = 1 24 ( K G P G ( t ) + K B a P B a ( t ) + K g r i d P g r i d ( t ) ) f_c=\sum _{t=1}^{24}\left(K_GP_G(t)+K_{Ba}P_{Ba}(t)+K_{grid}P_{grid}(t)\right) fc=t=1∑24(KGPG(t)+KBaPBa(t)+KgridPgrid(t))
KG = 0.3;
KBa = 0.2;
Kgrid = 0.5;
Objective = 0;
for i = 1:T
Objective = Objective + KG * P(1,i) + KBa * P(2,i) +Kgrid * P(3,i);
end
4.优化设置
采用cplex求解器求解,设置如下:
ops = sdpsettings('solver','cplex');
result = optimize(Constraints,Objective,ops);
5.结果可视化
t = 1:24;
p = value(P);
figure(1)
plot(t,p(1,:),'r*-','Linewidth',1.5);hold on;
plot(t,p(2,:),'k*-','Linewidth',1.5);hold on;
plot(t,p(3,:),'b*-','Linewidth',1.5);hold on;
plot(t,ones(length(t)),'k--');hold on;
legend('发','蓄','网','0');
到此为止,就实现了对一个简单的微电网系统的简单建模和优化。出于快速建立解决问题的整体思路的考虑,尽可能地减少了各类约束条件,对目标函数也大幅简化。而实际的微电网运行需要考虑因素更多,这些因素会在以后的文章中出现。
结果与分析
设置风电、光伏出力和负荷需求如下:

所得结果如下:
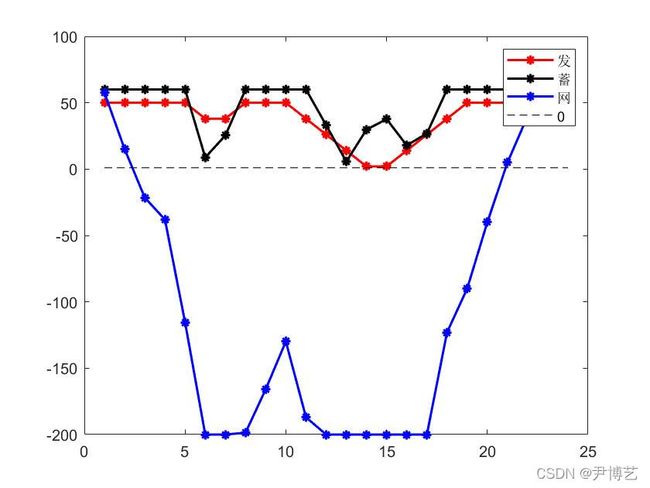
最终优化得到的总成本为:-731.11个单位。结果为负数,这并不奇怪,充分利用可再生能源,把满足负荷需求之外的电能售给电网是可以带来收益的。
写在最后
构建如此简单的模型是为了打基础,构建起解决微电网优化调度这一问题的总体思路,以后这个模型会不断完善,考虑更多的实际情况,达到更好的实际效果。
换言之,本文提出模型还只是一个Baby,关注“matlab & yalmip在微电网优化调度中的应用”这个系列,一起见证TA的成长吧。
数据来自:[1]王腾超. 含微电网的配电网日前能量优化[D].山东大学,2020.DOI:10.27272/d.cnki.gshdu.2020.006084.