02_07 python机器学习_第二章监督学习_核支持向量机

第二章监督学习_核支持向量机

核支持向量机的英文表示是: kernelized support vector machine 一般叫做SVM.
核:
 模型中有针对不同数据样本封装好的核方法,核应当指的就是这些函数.
核方法:
 在低维空间中不能线性分割的点集，通过转化为高维空间中的点集时，
从而变为线性可分的，这就是核方法。
核技巧:
 将低维空间处理不了的问题转化到高维空间来处理的技巧.
支持向量:
 SVM在学习过程中对每个计算对于决策边界的重要性,通常影响决策边界的只有小部分的数据点
这些点称作支持向量.
总结:
 使用核函数将低维空间难于处理的数据在处理高维空间进行解析处理的模型.

01 线性模型与非线性特征

---

SVM这个到倒是看到过,早在线性模型时就接触过,
不过当时书上只讲解了[LogisticRegression],另一个就是[LinearSVC]只是提到过.
他们都是线性模型,模型特点应当都差不多.把当时总结的内容拿出来再回忆一下.

LinearRegression优点:
 善于分析多特征数据
LinearRegression缺点:
 LinearRegression模型更多的是注重数据的线性趋势,因此在精度上会有一定的损失
 不适合特征数较少的数据
 不适合拥有多特征但大多是无效特征的数据
 没有参数来控制模型的复杂度,因此会出现训练集过拟合,测试集欠拟合的情况出现
LinearRegression使用建议:
 适合多特征且多数为有效的数据样本来预测数据的未来走势.

对于线性模型在针对较少特征数据样本表现不好上是有解决方案的.
书中给出的方案是添加非线性特征.
书中介绍两种方法

• 交互项
  一文轻松看懂交互作用
  比如: 既存特征A,B -> 扩张特征C=A*B 只是举个例子,实际可以更复杂
  简单理解就是:混杂多个特征.
• 多项式
  多项式百度词条
  由多个单项式构成.
  简单理解就是:不能直接拿到值,必须通过计算求值.

这两种方案都是通过现有数据特征,在原有数据样本中扩张出新特征的方法.
使用一个例子来说明.

01_001 非线性特征在线性模型[LinearSVC]中的显示效果

# 核支持向量机
# 共4个例子:
# 例子1: 线性模型&平面&分类
#   用于显示线性模型在平面上处理分类问题的不足.
# 例子2: 线性模型&3D空间&分类
#   在3D环境中观察线性模型处理多特征的效果
# 例子3: 线性模型&3D空间&分类&决策边界
#   演示在3D环境中如何正确施画决策边界
# 例子4: 线性模型&3D空间&分类&决策边界&超平面
#   演示如何在超平面中描述空间上的决策边界
import mglearn
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.svm import LinearSVC
from mpl_toolkits.mplot3d import Axes3D

# 创建4分类聚类数据
X, y = make_blobs(centers=4, random_state=0)
# 将4分类强行转变成2分类,(数据样本不变只y是改变了最终分类)
y = y % 2

##################################
# 在第一个画布上用线性模型构建平面图像
##################################
# 2特征4分类数据样本散点图和决策边界
# 获得新画布
fig1 = plt.figure()
# 取得当前画布的绘图对象
ax1 = plt.gca()
# 创建线性模型
linear_svc = LinearSVC().fit(X, y)
# 散点图
mglearn.discrete_scatter(X[:, 0], X[:, 1], y, ax=ax1, labels='LinearSVC')
# 平面决策边界
mglearn.plots.plot_2d_separator(linear_svc, X)


##################################
# 第二个画布上用线性模型构建3D图像
##################################
# 获得新画布
fig2 = plt.figure()
# 在新画布上创建3d绘图对象
# 参数: (这俩参数是控制表示角度的,不用记,用时自己调一调就行)
#   elev: 方位角
#   azim: 仰角
ax2 = Axes3D(fig2, azim=-158, elev=-176)
# 现在的数据不是只有两分类了吗,这里用了一个投机取巧的办法来区分这两类数据
# mask -> True 代表第一类数据
# ~mask -> False 代表第二类数据
mask = y == 0
# 为了填充3D模型定义Z轴, 在元数据样本上扩张了新的非线性特征
# 新特征使用第二特征的平方
X_new = np.hstack([X, X[:, 1:] ** 2])
# 在3D绘图对象上绘制第一分类数据的散点图
# 前三个参数位置分别代表 X轴, Y轴, Z轴
# c: color  b:blue, r:red
# cmap: color function   mglearn.cm2(绘图包提供的绘图解决方案)
# s: size
# marker: 图标
ax2.scatter(X_new[mask, 0], X_new[mask, 1],
            X_new[mask, 2], c='b', cmap=mglearn.cm2, s=60)
# 在3D绘图对象上绘制第二分类数据的散点图
ax2.scatter(X_new[~mask, 0], X_new[~mask, 1],
            X_new[~mask, 2], c='r', marker='^', cmap=mglearn.cm2, s=60)
ax2.set_xlabel('feature0')
ax2.set_ylabel('feature1')
ax2.set_zlabel('feature1 ** 2')

##################################
# 第三个画布上画出3D图像的决策边界
##################################
# 用3特征数据样本创建线性模型
linear_svm_3d = LinearSVC().fit(X_new, y)
# g(x) = w1x1 + w2x2 + w3x3 + w4x4 + w0
# coef 各个特征系数 w1~wn
# intercept: 模型偏移量 w0
coef, intercept = linear_svm_3d.coef_.ravel(), linear_svm_3d.intercept_
# 获得新画布
fig3 = plt.figure()
# 在新画布上创建3d绘图对象
ax3 = Axes3D(fig3, elev=-176, azim=-158)
# 创建50个连续点, 点的取值范围为: 数据样本第一特征最小值-2 ~ 最大值+2
# 这个2的偏移就是想让线把特征都包住
xx = np.linspace(X_new[:, 0].min()-2, X_new[:, 0].max()+2, 50)
yy = np.linspace(X_new[:, 1].min()-2, X_new[:, 1].max()+2, 50)
# 使用两个坐标轴上的点在平⾯上画格
# 一般用于3d图像的网格采样的数据源
XX, YY = np.meshgrid(xx, yy)

# 分子部分:
#   是线性方程计算公式即: 各特征*相应的特征系数之和 + 偏移量
# 分母部分:
#   Z轴系数
# 合在一起:
#   使用斜率公式求出网格线中每个点的空间高度即Z轴的位置
ZZ = (coef[0] * XX + coef[1] * YY + intercept) / -coef[2]
# 在3D绘图对象上绘制平面
# rstride: row stride 行间距
# cstride: column stride 列间距
# 含义查了半天都不如看一下代码来的直接
# def plot_surface(....)
#   row_inds = list(range(0, rows-1, rstride)) + [rows-1]
#   col_inds = list(range(0, cols-1, cstride)) + [cols-1]
# 看代码含义因该是在row或column范围内每个一定的步长抽一个点
# 因为抽取的范围是刨除掉边界点的,因此不影响大小,仅仅是为了少点计算量
ax3.plot_surface(XX, YY, ZZ, rstride=10, cstride=10, alpha=0.3)
# 在3D绘图对象上绘制第一分类数据的散点图
ax3.scatter(X_new[mask, 0], X_new[mask, 1], X_new[mask, 2], c='b',
            marker='^', cmap=mglearn.cm2, s=60)
# 在3D绘图对象上绘制第二分类数据的散点图
ax3.scatter(X_new[~mask, 0], X_new[~mask, 1], X_new[~mask, 2], c='r',
            marker='^', cmap=mglearn.cm2, s=60)
ax3.set_xlabel('feature0')
ax3.set_ylabel('feature1')
ax3.set_zlabel('feature1 ** 2')

##################################
# 第四个画布, 在超平面上绘制线性模型在3d空间中表示的决策边界
##################################
# 获得新画布
fig4 = plt.figure()
# 取得当前画布的绘图对象
ax4 = plt.gca()
# (1)新做成3D空间上的网格线 用新型模型进行分类,
# (2)分类产生的决策边界(3D空间)转换成各个超平面绘图数据
#   参数的shape必须与线性模型的shape一致因此需要在XX,YY基础上扩张出ZZ
#   ZZ的计算规则应与线性模型建模时的规则一致
# 什么是超平面?
#   https://baike.baidu.com/item/%E8%B6%85%E5%B9%B3%E9%9D%A2
ZZ_1 = YY ** 2
dec = linear_svm_3d.decision_function(
    np.c_[XX.ravel(), YY.ravel(), ZZ_1.ravel()])
# 绘制等高线图
#   采样上面产生的3D各个超平面的绘图数据,根据数据画出超平面轮廓
# 什么是等高线图?
#   https://baike.baidu.com/item/%E7%AD%89%E9%AB%98%E7%BA%BF/1697067?fr=aladdin
# contourf函数帮助:
#   https://ww2.mathworks.cn/help/matlab/ref/contourf.html#mw_e930b555-4fc5-4db1-8907-5d10f7aac1c0
# 前3个参数含义:  contourf(X,Y,Z) 指定 Z 中各值的 x 和 y 坐标。 等高线图的数据源
# level: 采样数据源那些位置用于绘制
ax4.contourf(XX, YY, dec.reshape(XX.shape), levels=[dec.min(), 0, dec.max()],
             cmap=mglearn.cm2, s=0.5)
# 绘制散点图
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
ax4.set_xlabel('feature0')
ax4.set_ylabel('feature1')

# 显示画布
plt.show()

01_002 非线性特征在线性模型[LinearSVC]中的显示效果分析

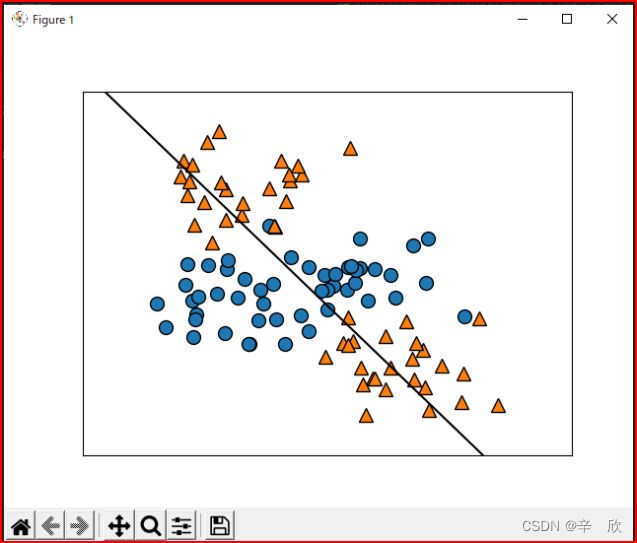
• 线性模型LinearSVC平面图像
  在创建LinearSVC模型时,我们强制将4分类数据的最终分类变成了2类,
  线性模型的特点是用一条直线来预测数据趋势或分割两分类.
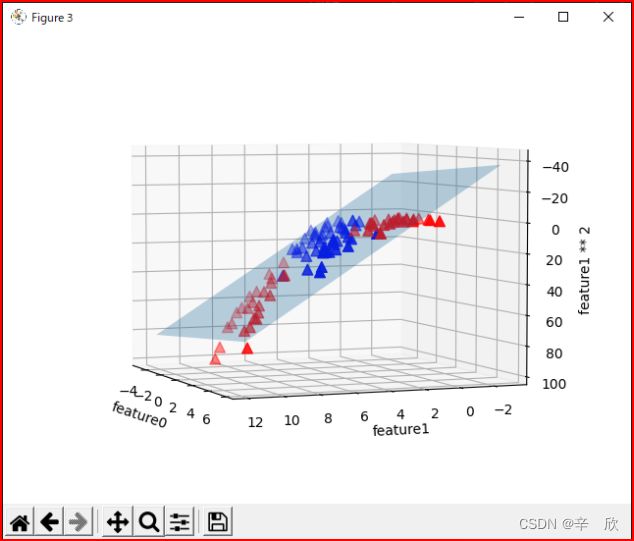
  因此对于本应是4分类的数据强行画一条线分割,在平面上很难看出类别间的决策边界.
• 线性模型LinearSVC 3D图像
  因为想用3D图像表示特征的空间位置,因此需要构建出新的特征来放在Z轴(原来只有平面的X,Y轴)
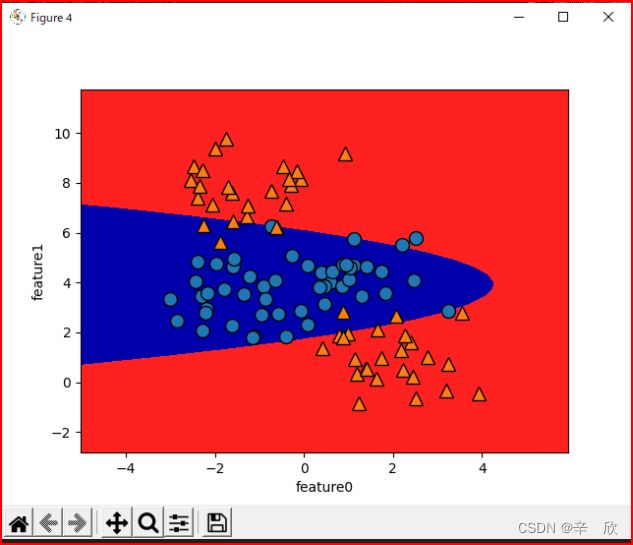
  通过3特征构建出3D图像可以清晰的看见这些特征的空间位置.
• 线性模型LinearSVC 3D空间的决策边界
  通过在空间绘出分类的决策边界,很容易将类别区分开.
• 超平面上绘制3D决策边界抽样的等高线图
  吃用3个等高线堆叠的方式将3d空间的决策边界画出来,成像效果是椭圆部分

01_003 例子中涉及的知识点

• 什么是向量
• 什么是内积/点集
• 什么是斜率
• 什么是单项式
• 什么是多项式
• 什么是欧式距离
• 什么是超平面
• 什么是超平面 通俗易懂
• contourf 填充二维等高线图函数帮助
• 什么是等高线

02 核技巧,核方法,核函数

什么是核技巧,核方法,核函数

03 支持向量

import mglearn
from sklearn.svm import SVC
from matplotlib import pyplot as plt

# 生成快速演示数据 2分类2特征
X, y = mglearn.tools.make_handcrafted_dataset()
# kernel: 核函数
# kernel='rbf' 不设置默认也是这个, 高斯核,
# C 精确系数, 越大越精确, 泛化越弱
# gamma 高斯核宽度, gamma越小核半径越大,gamma越大核半径越小
#   核半径越大模型越简单,核半径越小模型越复杂
svm = SVC(kernel='rbf', C=10, gamma=0.1).fit(X, y)
mglearn.plots.plot_2d_separator(svm, X, eps=.5)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
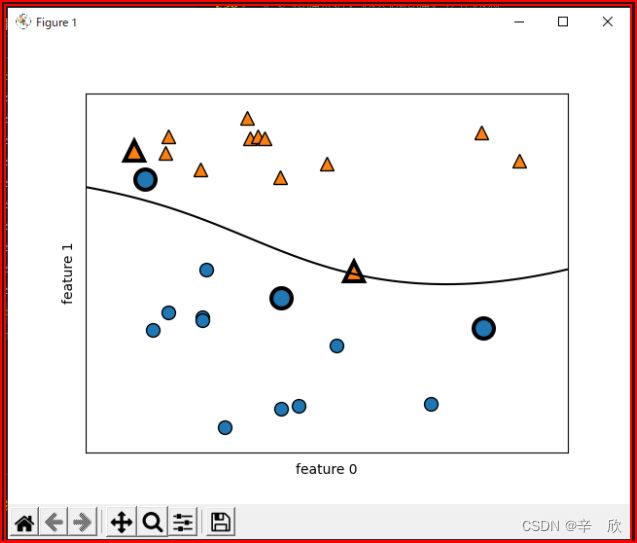
# 取得对决策边界有决定性作用的支持向量
sv = svm.support_vectors_
# 取得支持向量的参数重要度得分
sv_label = svm.dual_coef_.ravel() > 0
# 用散点图表示支持向量 size设置成15用于区分默认图标
mglearn.discrete_scatter(sv[:, 0], sv[:, 1], sv_label, s=15, markeredgewidth=3)
plt.xlabel('feature 0')
plt.ylabel('feature 1')
plt.show()

运行时关键信息

In [2]: sv
Out[2]: 
array([[ 8.1062269 ,  4.28695977],
       [ 9.50169345,  1.93824624],
       [11.563957  ,  1.3389402 ],
       [10.24028948,  2.45544401],
       [ 7.99815287,  4.8525051 ]])

In [4]: svm.dual_coef_
Out[4]: 
array([[-10.        ,  -6.25178295,  -3.73381586,  10.        ,
          9.98559881]])

03 核支持向量机 参数C & 参数gamma

# 核支持向量机
# 快速演示 模型参数C, gamma对于模型的影响

import mglearn
from sklearn.svm import SVC
from matplotlib import pyplot as plt

# 生成 3 * 3 绘图对象
fig, axes = plt.subplots(3, 3, figsize=(15, 10))

# 设定每组绘图对象中C的取值
for ax, C in zip(axes, [-1, 0, 0]):
    # 设定每个绘图中gamma的取值
    for a, gamma in zip(ax, range(-1, 2)):
        # 这个就是为了快速演示用的模型
        # 传入的参数都被设定为 10为底,参数为指数来求幂
        # 另外数据源是自动做成的,不用另外做成
        mglearn.plots.plot_svm(log_C=C, log_gamma=gamma, ax=a)

# 设定说明
axes[0, 0].legend(['class 0', 'class 1', 'sv class 0', 'sv class 1'],
ncol=4, loc=(.9, 1.2))

# 显示画布
plt.show()

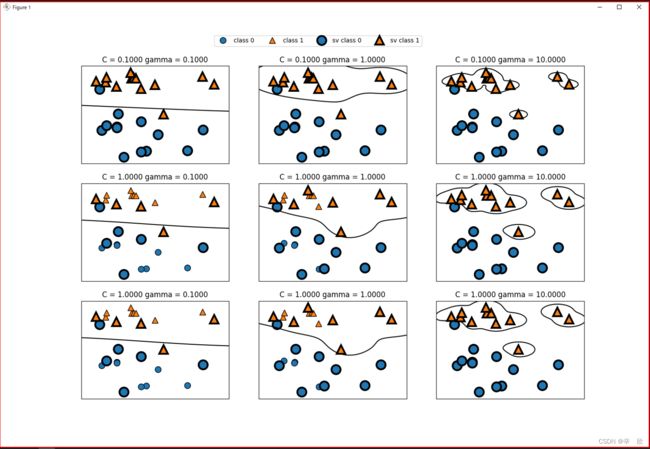
横向在相同精度C下观察半径gamma对于模型的影响,纵向观察相同半径gamma下精度C对于模型的影响.
通过观察发现:

参数	参数说明
[C] 精度参数	C影响的是决策边界与向量支持的距离. C越大,决策边界划分的越精确,边界越清晰可见,泛化能力越弱"
"[gamma]高斯核宽度 简单理解:气球半径	观察gamma是不能停留在2维空间的,应当在高维空间去考虑这个参数,简单点考虑可以想象一个气球, gamma就是气球的半径,gamma越大气球越大,气球越大使劲越大也就意味着模型越复杂, 随着gamma(气球)的逐渐增大,各个数据点也逐渐清晰,决策边界也越来越容易划分,太精确必将导致过拟合.

04 数据缩放 归一化

为什么要进行数据的缩放,建议先看看这个博客.

数据缩放[归一化]的原理是想办法将特征数据控制在0~1之间.
书上的做法:
1.求出各特征的最小值 array.min()
2.求出范围, 范围=(用各特征 - (1) ).max() 即各特征的范围
3.计算: ( 数据各特征-(1) ) / (2) 所以值一定在0~1之间

from sklearn.svm import SVC
# 数据样本
from sklearn.datasets import load_breast_cancer
# 数据样本分离
from sklearn.model_selection import train_test_split

#############################
# 数据准备
#############################
# 获得数据样本对象
cancer = load_breast_cancer()
# 分离训练数据和测试数据,
# 分离后数据各种类比例与原始数据样本相同
# 加入随机种子保证每次的执行结果都不同
X_train, X_test, y_train, y_test = \
    train_test_split(cancer.data, cancer.target,
                     stratify=cancer.target, random_state=42)
#############################
# 模型1
#############################
svc1 = SVC().fit(X_train, y_train)
print("模型1训练得分: %s" % svc1.score(X_train, y_train))
print("模型1测试得分: %s" % svc1.score(X_test, y_test))

#############################
# 模型2 数据缩放
#############################
# 原理
# 1.求出各特征的最小值 array.min()
# 2.求出范围, 范围 = (用各特征 - (1)).max() 即各特征的范围
# 3.计算:  (数据各特征-(1)) / (2)   所以值一定在0~1之间

train_min = X_train.min(axis=0)
train_range = (X_train - train_min).max(axis=0)
train_compute = (X_train - train_min) / train_range
test_compute = (X_test - train_min) / train_range

svc2 = SVC().fit(train_compute, y_train)
# 这里需要注意下,因为已经改变了训练方式,因此在测试得分的时候应当使用同样rule的数据.
print("模型2训练得分: %s" % svc2.score(train_compute, y_train))
print("模型2测试得分: %s" % svc2.score(test_compute, y_test))

通过上文我们学习了两种数据扩张方法:

• 标准化数据扩张的思想:
  排除掉不重要的数据,集中体现重要数据,整体数据的波动范围稍大,
  标准化讲究的是集中体现重要数据,对个别的异常数据的容忍性比较好.

• 归一化数据扩张的思想:
  一个都不能少[异常数据也包含其中],全部按比例缩放到0~1区间,因此整体数据的波动范围很小
  这么小的波动范围一个小小的噪点就能影响整个预测结果,
  因此归一化讲究的是完整性,它对异常数据敏感.

结合上面的特性去理解下面的表格:

算法模型	推荐:标准化数据扩张	推荐:归一化数据扩张
线性和逻辑回归	〇
神经网络	〇
支持向量机	〇
K均值聚类	〇
K最近邻居	〇
主成分分析	〇
分类和回归树		〇
森林随机回归		〇

05 线性模型(核支持向量机)总结

• 优点:

  • 核函数丰富,可以针对不同的数据使用不同的核来处理,因此对各种数据集的表现都很好
  • 允许数据的决策边界很复杂(因为模型可以使用高维空间处理低纬空间很难处理的问题)

• 缺点

  • 对数样本个数的缩放不好,当数据样本个数达到10万以上的时候,是非常考验机器性能的
  • 波动大的数据样本需要做数据的预处理(数据缩放)
  • 不同核有不同的参数,例如C和gamma,这些参数的微小变化都能直接影响模型结果,
    设置比较复杂, 而且为了调校至合适值可能需要多次的训练尝试.

  模型适合处理的数据: 数据量适中,数据特征的单位相似且整体的波动范围不大,对数据特征的多少并无要求.

以上