粒子群算法原理|python实现|参数调优

粒子群算法是比较有名的群体智能算法之一，其他群体智能算法还包括蚁群算法、鱼群算法、人工蜂群算法等。今天学习一下粒子群算法。

算法原理（Inspiration）

粒子群算法来源于鸟群的觅食行为，一群鸟随机寻找区域内唯一食物的位置，粒子群算法中的粒子就是鸟群中的小鸟。

该算法最重要的三个变量即每只鸟拥有的信息：
当前位置（向量X）、
自己当前位置距离食物的距离（适应度P，即当前X对应的目标函数值Y）、
飞行速度（向量V，即下一步X调整的方向和速度）。

优化过程

1. 初始化
   与大多数机器学习算法一样，粒子群算法的初始值随机确定。
   初始值包括鸟群的初始位置(即X) X[popsize,num_variables]，
   初始位置对应的适应度(即目标函数值y) fitness[popsize]，
   初始速度 V[popsize]*；

2. 计算当前个体最优(即每只鸟所取得过的y中的最优值) fitnessinbest[popsize]、
   个体最优对应的位置(即X) inbest[popsize,num_variables]、当前整体最优(即所有鸟取得过的y中的最优值) fitnessglbest、
   整体最优对应的位置 glbest[num_variables]。

   其中，popsize表示鸟群中鸟的数量，num_variables表示问题中自变量的个数，如一元函数中num_variables为1，二元函数为2，等等。

3. 迭代更新
   在每次鸟群按照当前速度飞行一个单位时间（即一次迭代）后，所有粒子共享信息，从而计算出自己飞行到的所有地方中距离食物最近的点（局部最优）和所有鸟群飞到的位置中距离食物最近的点（全局最优），并计算加权平均决定下一步飞行的速度和位置。

   速度和位置的更新公式如下：

   $V^{k+1}=w{V}^k+c_1{r}_1(inbes{t}_{id}^k-X_{id}^k)+c_2{r}_2(glbes{t}^k-X_{id}^k)$
   $X_{id}^{k+1}=X_{id}^k+V_{id}^k$

   其中V表示速度，X表示个体位置，w,c,r为参数，上标k和k+1表示当前迭代和下一次迭代，inbest表示局部最优，glbest表示全局最优。
   同时，一轮迭代结束后，对个体最优和全局最优进行更新，即更新inbest、glbest、fitnessinbest和fitnessglbest。

4. 经过多轮迭代，即可得到glbest和fitnessglbest。

python实现

初始化
V表示速度矩阵，population表示自变量矩阵，fitnessinbest表示个体最优值，fitnessglbest表示全局最优值，inbest和glbest是其分别对应的自变量取值。使用随机策略进行初始化：

#initialize particles and speeds randomly
population=np.ones((sizepop,num_variable))# value of x 
V=np.ones((sizepop,num_variable))# speed
fitness=np.ones(sizepop)#value of y
for i in range(sizepop):# for each particle(row)
    for j in range(num_variable):# for each xi(col)
        population[i][j]=random.uniform(popmin,popmax)#consistent with the range of x
        V[i][j]=0.5*random.uniform(-1,1)#consistent with the range of speed
    fitness[i]=function.fun(population[i])
#calculate initial optimal values
fitnessinbest=copy.deepcopy(fitness)# local optimum y
fitnessglbest=max(fitness)#global optimum y
bestindex=list(fitness).index(fitnessglbest)#index of global optimum
glbest=population[bestindex]# the x corresponding to fitnessglbest
inbest=copy.deepcopy(population)# the x corresponding to fitnessinbest

迭代
最外层循环使用i表示迭代次数，动态策略更新权重，第二层循环使用j表示各个粒子，最内层循环使用k表示自变量个数，进行迭代更新：

#iterate for optimization
for i in range(maxgen):# for each iteration
    w=ws-(ws-we)*(i/maxgen) #for the other functions,dynamic w performs better
    for j in range(sizepop):# for each particle
        #update the speed
        V[j]=w*V[j]+c1*random.random()*(inbest[j]-population[j])+c2*random.random()*(glbest-population[j])
        for k in range(num_variable):
            if(V[j][k])>Vmax:
                V[j][k]=Vmax
            elif(V[j][k]<Vmin):
                V[j][k]=Vmin
        #update the location
        population[j]=population[j]+V[j]
        for k in range(num_variable):
            if(population[j][k])>popmax:
                population[j][k]=popmax
            elif(population[j][k]<popmin):
                population[j][k]=popmin
        #update the fitness
        fitness[j]=function.fun(population[j])

更新个体最优和全局最优
遍历每个粒子，计算其函数值是否是目前的个体最优或全局最优，若是则更新：

for j in range(sizepop):# for each particle
    #update the inbest
    if(fitness[j]<fitnessinbest[j]):
        inbest[j]=population[j]
        fitnessinbest[j]=fitness[j]
    #update the glbest
    if fitness[j]<fitnessglbest:
        glbest=population[j]
        fitnessglbest=fitness[j]

参数调优

粒子群算法涉及到的参数有：

parameter	meaning
w	速度更新时惯性的权重
c1, c2	速度更新时个体经验、群体经验的权重
maxgen	最大搜索轮数
popsize	群体中个体数量
Vmax	飞行速度的最大值
Vmin	飞行速度的最小值
num_variable	自变量维度

我们以六个常用函数为例，进行参数调优测试：

w参数的设置

根据速度更新公式，w表示速度更新时惯性的权重，即保持当前飞行速度的权重，主要影响粒子迭代速度的转角，与转角成反相关。在进化过程中，w决定了粒子搜索的多样性，w较大时全局搜索能力强，局部搜索能力弱，体现出粒子运动的“震荡性”；w取值较小时局部搜索能力强，全局搜索能力弱。w取值过大可能导致无法收敛到精确解，w取值过小时容易造成局部收敛。因此，平衡收敛速度与搜索精度需要动态调整权重，初始时w较大，增强全局搜索能力，随着搜索轮数增加，逐渐减小w，从而取得最优解。实验采用典型线性递减策略 进行测试，并将实验结果与恒定w的结果进行比较。
典型线性递减策略中w更新公式如下：
$$w=ws-\frac{(ws-we{)}^i}{maxgen}$$
其中，ws为初始权重（最大值），we为最终权重（最小值），i为搜索轮数。前人研究表明，w取值范围在[0.4，0.9]时效果较好。
图 绘制出6个目标函数在不同的w策略下的迭代情况，横轴表示迭代次数，纵轴表示计算误差的平方。为清晰地看出曲线间的关系及变化趋势，图3.2截取了原始图像的一部分，将曲线学习开始时误差值较大的部分和学习后期趋于稳定的部分截去，将变化趋势较为明显的部分展示如下：

w参数调优图

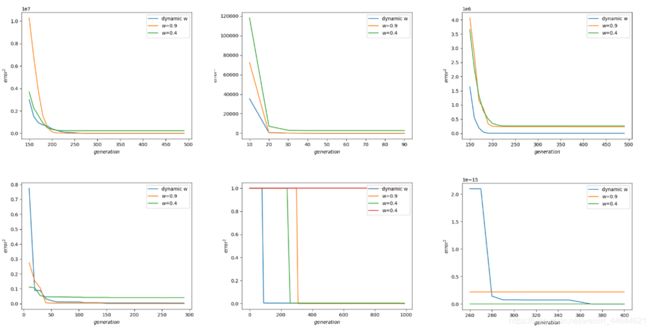
对每种参数取值方法进行多次试验的结果显示，w取值较小且恒定时（图中绿色曲线），对于function1-function4，在搜索轮数达到5000后仍距离最优值较远，说明其全局搜索能力较差；对function5，w取值0.4时试验结果分为差异较大的两类，分别用红色和绿色曲线表示，说明求解结果受随机初始值影响较大，也是由于局部收敛问题导致的；对function6，多次试验结果都快速收敛于最优值，在收敛速度和精度上表现都最优，根据图3.2绘制的函数图像，function6与其他函数的形状有显著差别，其随机初始值更接近最优解的概率更大，因此也表现出了与其他函数不同的性质。
w取值较大且恒定时（图中橙色曲线），function1、2、4、5都表现出较好的全局收敛能力；function3的收敛速度较慢，但在搜索轮数达到5000轮时收敛到了比线性递减策略更为精确的最优解；而function6却未能在5000轮的搜索中收敛，说明其局部搜索能力仍存在欠缺。由此可以看出，对于不同性质的函数w取值的影响有所不同。
对w使用动态递减策略时，对各方程都能够较好地收敛于最优值，且收敛速度较快，是一种适用于多数问题的参数设置策略，但对于不同问题仍需取不同的参数。此外，除线性递减策略，w的取值还有非线性递减策略、先增后减策略、自适应取值策略等动态取值的方法，每种方法各有优缺点，需要根据问题的实际情况选取最优策略 。

参数$c_i$的设置

速度更新公式中的c1、c2主要影响粒子对个体经验和群体经验的信任程度。c1代表了粒子的个体意识，而c2代表了粒子的群体意识 。在进化过程中，c1相对越大，粒子的搜索空间越分散，收敛速度也越慢，甚至算法会停滞为无法收敛；而c2相对越大，粒子越快地趋向同一个位置，但容易早熟收敛而错过最优解，尤其当w和c1同时较小时，粒子将直接飞向glbest。

参数 ci 调优图

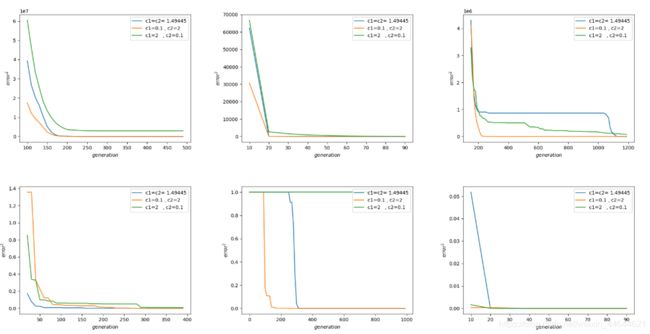
上图绘制了6个目标函数在c1、c2分别取c1=c2、c1>c2、c1 对于c1=2，c2=0.1的情况，即图中的绿色曲线，由于粒子的“个体意识”过强，“群体意识”过弱，算法的收敛速度在各函数中的表现比其他两种情况更慢，尤其对于function5这类随机搜索结果接近最优值的概率很小的函数，c1取值过大而c2取值过小会使得算法性能表现极差。
对于c1=0.1，c2=2的情况，对应图中的橙色曲线。对于研究的6个目标函数，这种参数设置的情况下收敛速度最快，且并没有出现早熟收敛而错过最优解的现象。但是当w的取值同时较小时（如w=0.4），各函数均无法收敛至最优解。由此可见，各参数的调整需要协调配合。
对于c1=c2=1.49445的情况，即图中蓝色曲线，对各目标函数都能收敛至最优解，且收敛速度较快。尽管在部分函数搜索过程中表现出的搜索速度不如c1=0.1，c2=2时快，但是一种可靠、对绝大多数函数有效的取值办法，在多数案例中广泛应用。

速度范围的设置

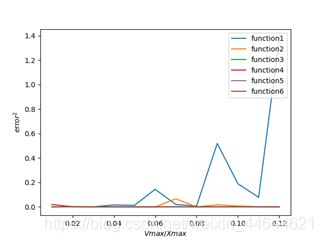
已有研究证明，粒子群算法中最大速度的选择不仅与问题本身性质有关，与自变量的取值范围也有密切关系。文献 中提出了最佳速度因子u，用于表示速度与自变量取值范围的比值，并使用四个函数进行实验，得出u的最佳范围为(0.059, 0.112)的结论。其中
$$u=\frac{Vmax}{Xmax}$$
以u为横轴，误差的平方为纵轴，绘制本实验6个函数的图像如图3.4所示，平均误差最小时参数U、Vmax的取值范围见下表。

速度范围调优图

速度范围调优表

	fun1	fun2	fun3	fun4	fun5	fun6
min_error	3.81E-05	1.12E-08	0	1.55E-07	0	0
u	0.01	0.01	\	0.13	\	\
Vmax	1	0.1	\	0.16	\	\

由图，不同函数的搜索误差对速度范围参数的敏感度有很大差异，在其他参数不变时，function1和function2受速度范围影响较大，function4受速度范围影响较小，而function3、5、6的搜索误差并没有随速度范围的改变而改变。
本实验与文献iv均使用了function1函数作为测试函数，但得出的最优参数值u有很大差异。文献iv取自变量范围为[-10,10]，得出最优u值为0.1的结论；在本实验中自变量取值[-100,100]，此时最优u值为0.01，但两实验中Vmax的最优值都为1。由此可见，速度与自变量取值的比值虽然对速度范围的调整有一定参考意义，但仍需要根据自变量的取值范围综合考虑。本实验与文献iv得出的共同结论是，对于不同函数Vmax值有较大差异，需要根据问题实际情况决定。

种群规模的设置

通过阅读相关文献，部分学者认为搜索精度对种群规模并不敏感 ；也有学者认为种群规模的选取与问题维度有关，且其搜索结果会同时影响到搜索时间和精度 。本实验以function1为例，探究种群规模与问题维度、搜索精度、搜索时间的关系。
下表展示了function1在dimension取10、50、100时不同种群规模（sizepop）对搜索精度的影响。与文献v结论相吻合，在问题维度较小时，种群规模对搜索精度有较大影响；而维度大于40时，搜索精度对种群规模不再敏感，尤其是当维度取100时，过大的种群数量可能对搜索精度产生不好的影响。

种群规模调优表

$erro{r}^2$	sizepop=10	sizepop=40	sizepop=70	sizepop=100
dimension=10	1.10E-05	1.96E-10	3.85E-12	2.85E-10
dimension=50	49.42885	0.04744	0.013147	0.010596
dimension=100	3285.436	24.28372	1.707335	2.837563

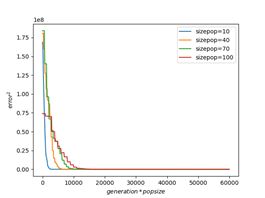
下图为function1在不同维度、不同种群规模下训练时间与训练精度的关系。由图可以直观地看出，当问题维度较小时，更大的种群规模可以得到更高的精度，同时搜索速度也越慢；而维度较大时，搜索速度对种群规模同样不再敏感。

种群规模调优图
综上所述，问题维度较大时，搜索精度对种群规模不敏感；维度较小时，若侧重于减少运行时间，可将种群规模设为40左右，若侧重搜索精度，可设置为50~80，过高的种群规模不再对问题精度起到明显提高作用。

算法结果

使用粒子群算法得到的优化目标值见表：

算法结果

function	1	2	3	4	5	6
optimization	1.7e-6	1.6e-5	0.0	7e-4	-1.0	0.0