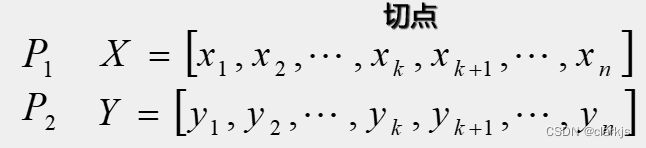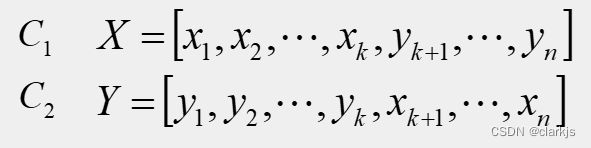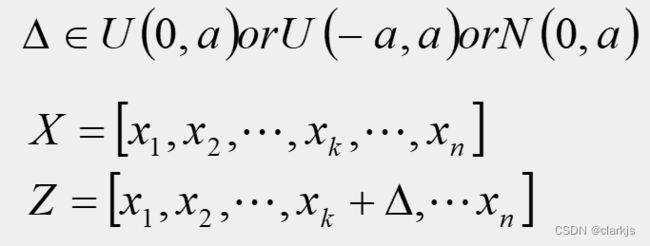机器学习之遗传算法

一、遗传算法流程

遗传算法（Genetic Algorithm，GA）最早是由美国的 John holland于20世纪70年代提出,该算法是根据大自然中生物体进化规律而设计提出的。是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法。该算法通过数学的方式,利用计算机仿真运算,将问题的求解过程转换成类似生物进化中的染色体基因的交叉、变异等过程。在求解较为复杂的组合优化问题时,相对一些常规的优化算法,通常能够较快地获得较好的优化结果。遗传算法已被人们广泛地应用于组合优化、机器学习、信号处理、自适应控制和人工生命等领域。

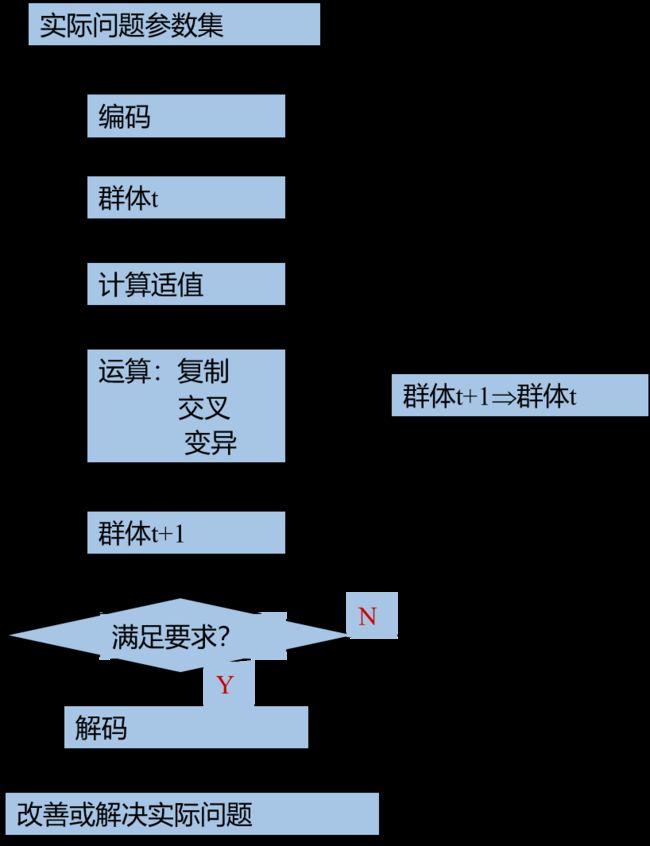
二、通过例子理解遗传算法

1. 个体编码

遗传算法的运算对象是表示个体的符号串，所以必须把变量 x1, x2 编码为一种符号串。本题中，用无符号二进制整数来表示。
因 x1, x2 为 0 ~ 7之间的整数，所以分别用3位无符号二进制整数来表示，将它们连接在一起所组成的6位无符号二进制数就形成了个体的基因型，表示一个可行解。
例如，基因型 X＝101110 所对应的表现型是：x＝[ 5，6 ]。

2. 初始种群的产生

遗传算法是对群体进行的进化操作，需要给其淮备一些表示起始搜索点的初始群体数据。
如：011101，101011，011100，111001

3. 适应度计算

遗传算法都需要构造适应度函数，适应度函数类似生物个体对环境的适应能力，一般来说，适应度函数越大越好，因此，此例中我们可以直接将目标函数作为适应度函数。

4. 选择运算

选择运算(或称为复制运算)把当前群体中适应度较高的个体按某种规则或模型遗传到下一代群体中。一般要求适应度较高的个体将有更多的机会遗传到下一代群体中。
我们不难注意到一个词 —— “更多机会”，听起来很简单，那具体怎么实现呢？怎么使得天选之子更偏向于适应度函数更大的那些个体呢？推荐一种方案 —— 轮盘赌，如下图所示：

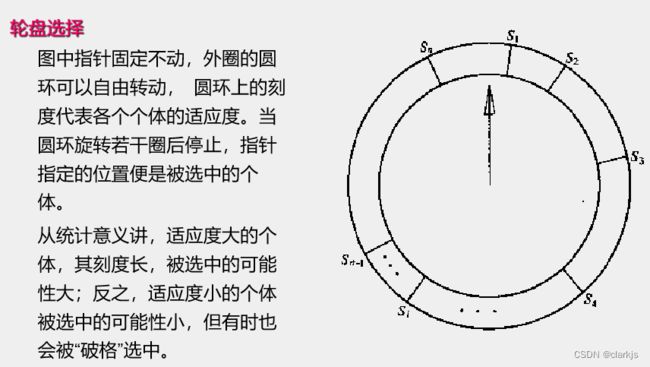
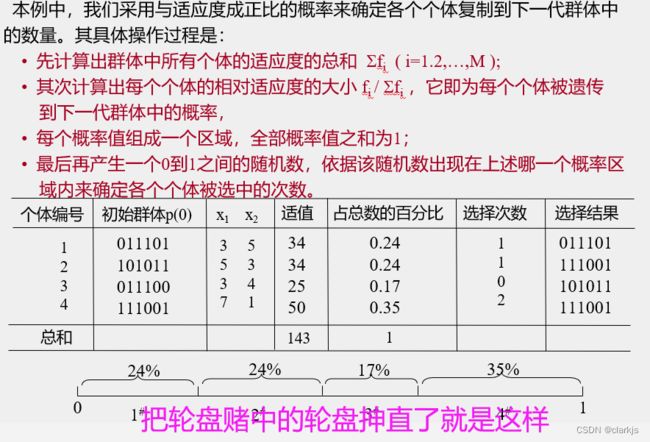
5. 交叉运算

交叉运算是遗传算法中产生新个体的主要操作过程，它以某一概率相互交换某两个体之间的部分染色体。
本例采用单点交叉的方法，其具体操作过程是：（1）先对群体进行随机配对；（2）随机设置交叉点位置；（3）最后再相互交换配对染色体之间的部分基因。

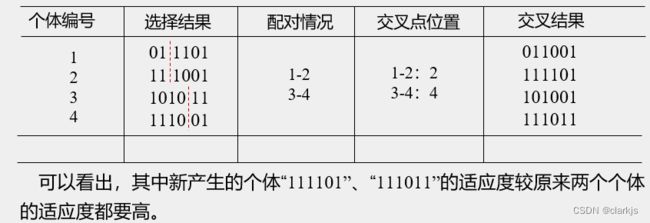
6.变异运算

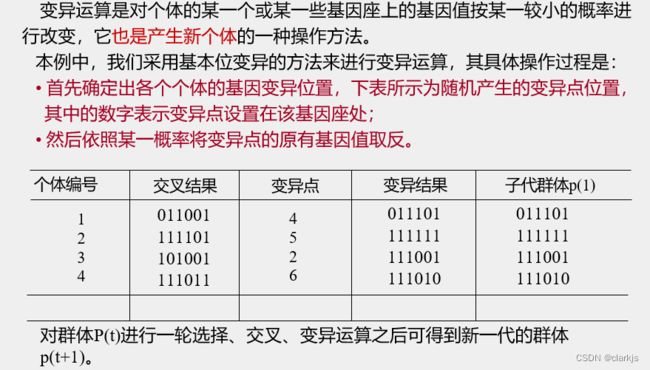
从上表中可以看出，群体经过一代进化之后，其适应度的最大值、平均值都得到了明显的改进。事实上，这里已经找到了最佳个体“111111”。

三、遗传算法知识点

1. 编码方式

（1）顺序编码

用1到N的自然数的不同顺序来编码，此种编码不允许重复。该法适用范围很广：指派问题、旅行商问题和单机调度问题等等。合法性问题：是否符合采用的编码规则的问题。

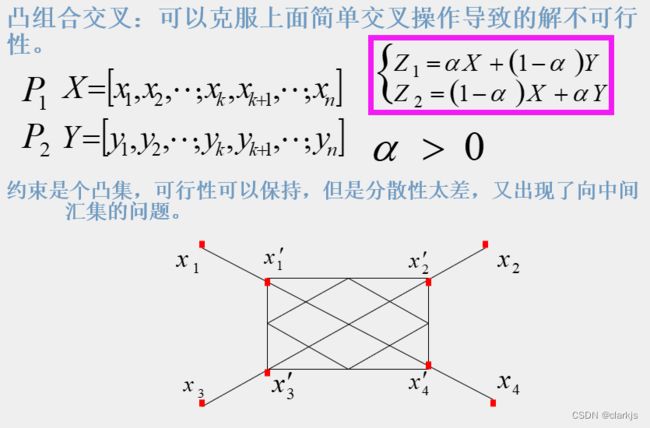
（2）实数编码

方便，运算简单，但反映不出基因的特征.

（3）整数编码

整数编码类似顺序编码，唯一的区别是：顺序编码不允许重复，但整数编码允许重复。

2. 适值函数的标定

1. 标定的目的：使得适值函数不太大，并且有一定差别

（1）选择压力

选择压力是种群好、坏个体被选中的概率之差，差大称为选择压力大。

（2）局部搜索、广域搜索与选择压力的关系

局部搜索与广域搜索是GA中的一对矛盾，只注重局部搜索很可能陷入局优，只注重广域搜索则会导致精确开发能力不强。因此，好的算法要将以上二者综合考虑。一般来说，算法开始时应注重广域搜索，通过使用较小的选择压力来实现；随着迭代的进行，逐步偏重于局部搜索，通过使用较大的选择压力来实现。

2. 适值的标定方法

这里将介绍6种适值函数的标定：（1）线性标定；（2）动态线性标定；（3）幂律标定；（4）对数标定；（5）指数标定；（6）窗口技术

（1）线性标定

（2）动态线性标定

动态线性标定(最常用)：线性标定中的参数随着迭代次数的增加而变化时就得到了动态线性标定

（3）幂律标定

（4）对数标定

（5）指数标定

（6）窗口技术

补充：

3. 选择策略

（1）截断选择

选择最好的前T个个体，让每一个有1/T的选择概率，平均得到NP/T个繁殖机会。
缺点：这种方法将花费较多的时间在适应值的排序上。

（2）顺序选择

（3）正比选择

4. 停止准则

四、遗传算法中的问题

1. 顺序编码

（1）交叉修复策略

① 部分映射交叉

② 顺序交叉

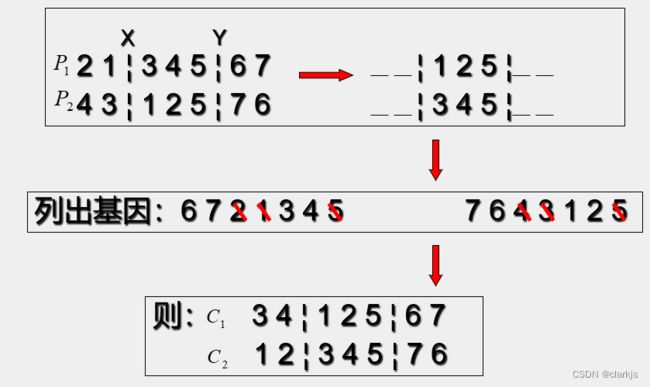
OX的特点： 较好的保留了相邻关系、先后关系, 满足了TSP问题的需要,但不保留位值特征。

③ 循环交叉

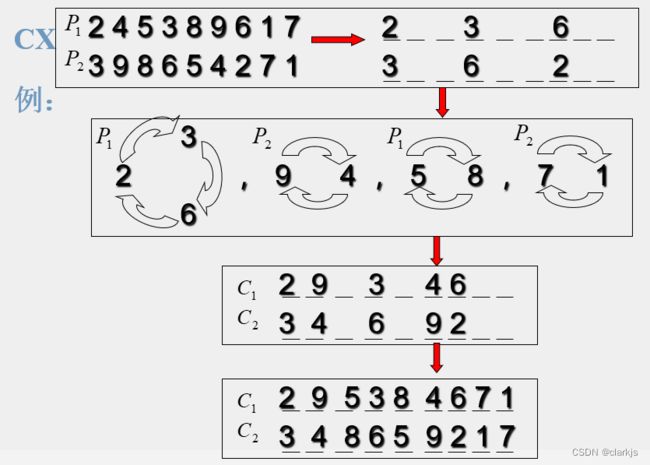
CX特点：与OX的特点不同的是， CX较好的保留了位值特征，适合指派问题；而OX较好的保留了相邻 关系、先后关系满足了TSP问题的需要。

（2）变异的修复策略

① 换位变异

换位变异(最常用)是随机地在染色体上选取两个位置，交换基因的位值。
例： 4 3 1 2 5 6 7 -------- > 4 5 1 2 3 6 7

② 移位变异

任选一位移到最前面。
例： 4 3 1 2 5 6 7 ------- > 5 4 3 1 2 6 7

2. 实数编码

（1）交叉

① 单切点交叉

② 双切点交叉

③ 凸组合交叉

（2）变异

① 位值变异：任选一位加Δ（变异步长）

② 向梯度方向变异