线性回归模型异方差解决方法

1.异方差定义

传说在多元线性回归有这一基本假设:

1. 模型符合线性模式
2. X满秩（无多重共线）
3. 零均值价值：$E({\xi }_i|X_i)=0$（自变量外生）
4. 同方差：$Var({\xi }_i|X_i)=\sigma$
5. 无自相关：$cov({\xi }_i,{\xi }_j)=0$

如果模型违反了相应的假设就会犯对应的错误，我们在计量经济分析中的检验就是检验出是否可能犯了某一类错误，如果极有可能犯了一种错误时，我们应该怎么修正它，才能保证分析的结果是有效的。

其中同方差就是一项要求，那与之同方差对应的就是异方差，也是我们在线性模型中常遇到的问题。
在线性模型中，我们把数据导入到模型中，生成出的线性直线，到实际每个数据垂直水平距离相差无几。这个就是同方差，例如下图第一张图。

同理异方差，就是实际每个数据点到线性直线的距离是不同的，例如下图后三张。

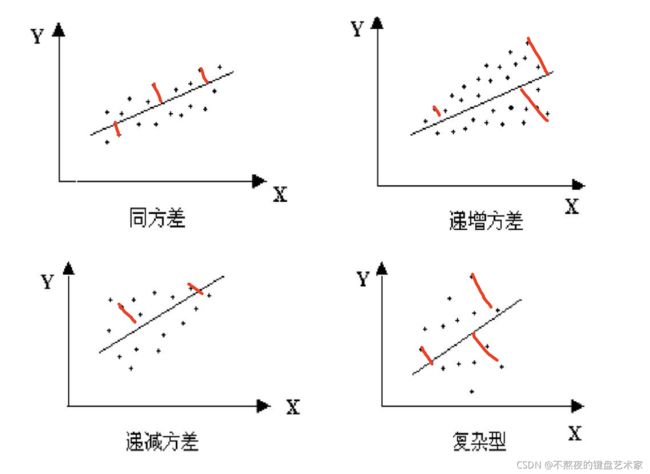
为什么要做异方差呢，因为实际我们在做回归分析回归分析和方差分析中都是假设样本之间是同方差的。在方差分析中，同方差是各组之间的方差相等；在回归分析中，同方差是指对于每一个样本点来说，随机误差的平方和(残差平方和)是一样的。

2.异方差检验

如果知道自己的做出的模型，是否存在异方差呢，那我们就需要去检验对吧，这里有如下方法科学的方法：

2.1 残差图

通过绘制残差图，残差图绘制是以残差平方和为纵坐标，一般以回归拟合值y作为横坐标，当然也可以以其他自变量x作为横坐标，通过直观观察分布规律。

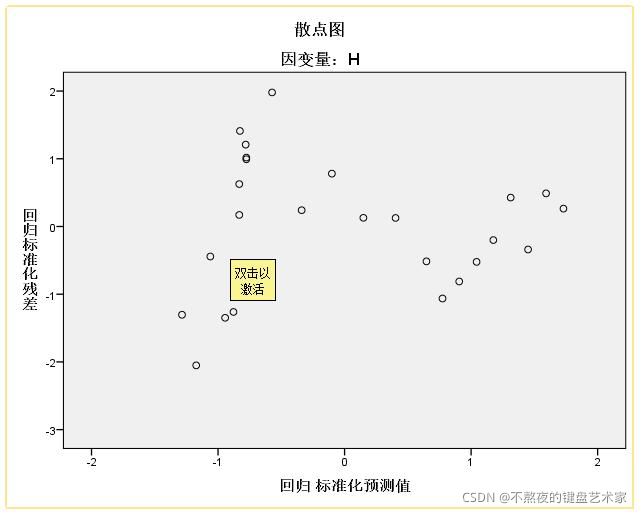
2.2 white检验

文字原理不解释了 直接告诉实际步骤吧

1. 步骤一：通过最小二乘法，计算得到原来这个线性模型的残差和。例如如下：
   $$Y_i={\beta }_1+{\beta }_2{X}_2+{\beta }_3{X}_2+u_i$$
   其中$u_i$就是残差
2. 步骤二，依据残差构造如下方程：
   $$u_i^2=a_1+a_2{X}_2+a_3{X}_2+a_4{X}_2^2+a_5{X}_2^2+a_6{X}_2{X}_2+v_i$$
   上面构造的方程看起来比较复杂，但主要是由三部分组成：原方程的解释变量、解释变量的平方、解释变量之间的交互项。
   方程构造好以后对方程进行估计求解。
3. 步骤三：换个角度思考一下，异方差实际就是残差项与某个x之间的相关性，如果步骤2中的方程中每一个系数都为0，是不是说明残差与任意x都是无关的，我们把这个称为原假设；反之，只要有一个系数不为0，就说明残差与x有关，也就是存在异方差，我们把这个称为备择假设。
   在原假设成立的情况下，可以得知步骤2中方程的$R^2$乘以样本容量n服从自由度等于步骤2回归方程中的变量数的卡方分布。
   在服从卡方分布的前提下就可以根据与卡方分布的临界值来比较来判断原假设是否成立。
4. 步骤4：
   如果计算出来的$n{R}^2$显著高于选定显著性水平(p_value值)的卡方临界值，则需要拒绝原假设，也就是方程存在异方差。
   如果存在异方差时，还可以查看step2方程的估计结果中每个变量的显著性情况，进而确定是哪个变量引起的异方差。

3.异方差修正

3.1 对原数据做对数处理

针对连续且大于0的原始自变量X和因变量Y，进行取自然对数（或10为底对数）操作，如果是定类数据则不处理。

取对数可以将原始数据的大小进行‘压缩’，这样会减少异方差问题。事实上多数研究时默认就进行此步骤处理。负数不能直接取对数，如果数据中有负数，研究人员可考虑先对小于0的负数，先取其绝对值再求对数，然后加上负数符号。

3.2 使用OLS稳健标准误回归

主要思路是将对异常值十分敏感的经典最小二乘回归中的目标函数进行修改。经典最小二乘回归以使误差平方和达到最小为其目标函数。因为方差为一不稳健统计量，故最小二乘回归是一种不稳健的方法。不同的目标函数定义了不同的稳健回归方法。常见的稳健回归方法有：最RANSAC（RANdom SAmple Consensus 随机采样一致性）和Theil-Sen estimator。

稳健回归对离群值的处理基于一个可设定的参数：容忍度。这个参数决定了模型会将哪些离群值剔除出训练数据。在下面介绍的算法中，都可以找到相应的此参数。

RANSAC 随机采样一致性算法

它通过多次随机采样，得到更准确的剔除离群值影响的模型。它的一种常见计算步骤如下：

• 随机选择n个样本点（n是人为指定的模型所需最小样本点数量）；
• 根据这些样本得出回归模型；
• 根据上一步得到的模型计算所有样本点的残差（residual），将残差小于预设残差阈值的点归为inlier，其余是outlier；
• 判断inlier数量是否达到预设的样本数阈值，如果达到则说明模型足够合理，如果未达到则重复上述步骤。

从上面的算法步骤就能看出，RANSAC算法的有效性很大程度上取决于迭代次数，但它大部分时候还是可以得到一个不错的结果。

下面是用 sklearn 库的 RANSACRegressor 类实现的一个代码示例。

# -*- coding: utf-8 -*-

# 引入所需库
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression, RANSACRegressor
from sklearn import datasets
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt

# 借用Boston Housing的数据
data = datasets.load_boston()

df = pd.DataFrame(data.data, columns=data.feature_names)

# 选择LSTAT这个特征作为示例
X = df['LSTAT'].values.reshape(-1, 1)
y = data.target

X_train, X_test, y_train, y_test = train_test_split(X, y)

# 普通线性回归
lin_model = LinearRegression()
lin_model.fit(X_train, y_train)
lin_y_pred = lin_model.predict(X_test)

# RANSAC回归
ran_model = RANSACRegressor()
ran_model.fit(X_train, y_train)
ran_y_pred = ran_model.predict(X_test)
inlier_mask = ran_model.inlier_mask_
outlier_mask = np.logical_not(inlier_mask)

# 评价两个模型的效果
plt.figure(figsize=(15,10))

plt.scatter(X_train[inlier_mask], y_train[inlier_mask], c='green', label='Inliers')
plt.scatter(X_train[outlier_mask], y_train[outlier_mask], c='red', label='Outliers')
plt.plot(X_test, lin_y_pred, '-k', label='LR')
plt.plot(X_test, ran_y_pred, '-b', label='RANSAC')
plt.legend(loc='upper right')
plt.show()

我们在做模型的时候，通常数据为dataframe格式，这种数据直接导入到模型是会报错的，比如说:

model.fit(df[‘x’],df[‘y’])，我们需要对数据进行改进，改为df[[‘x’]].values.tolist()和df[[‘y’]].values.tolist()

在statsmodels库还有一种更方便的ols模型，这种就不要担心数据结构导致模型不兼容的问题

import statsmodels.formula.api as smf

result = smf.ols('x~y',data=data1).fit()
print(result.summary())

3.3 WLS回归

FWLS回归也叫加权最小二乘法，加权最小二乘法(WLS)，加权最小二乘是在普通的最小二乘回归(OLS)的基础上进行改造的。

OLS一般公式如下：
$$Y_i={\beta }_1+{\beta }_2{X}_i+u_i$$
其中$u_i$为残差，在white检验中说过，残差的值与x取值存在关系，比如在研究年龄和工资收入的之间的关系时，随着年龄越大，$u_i$的波动是会越大的，所以公式上，我们要考虑不同x对$u_i$的影响，改进公式如下：
$$\frac{Y_i}{{\sigma }_i}={\beta }_1\frac{1}{{\sigma }_i}+{\beta }_2\frac{X_i}{{\sigma }_i}+\frac{u_i}{{\sigma }_i}$$

直白说，就是在线性方程在导入自变量的同时，增加一个自变量的权重，拟合模型。

代码实现有二种：

基于sklearn

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
x_traina,x_testa,y_traina,y_testa=train_test_split(df['x'],df['y'],test_size=0.2)
sample_weights=[(1/x) for x in x_train]
model1=model.fit(x_traina[['x']].values.tolist(), y_traina[['y']].values.tolist(),sample_weight=sample_weights)

基于statsmodels

import statsmodels.api as sm
from sklearn.linear_model import LinearRegression
x_traina,x_testa,y_traina,y_testa=train_test_split(df['x'],df['y'],test_size=0.2)
sample_weights=[(1/x) for x in x_train]
wls_model = sm.WLS(y_traina, x_traina, weights=sample_weights)
results = wls_model.fit()