【计算智能】读书笔记 第十章节 Part1 模拟退火算法

---

1. 算法思想

模拟退火 (Simulated Annealing , SA) 算法的基本思想 早在 1953 年就巳经由Metropolis 提出

模拟退火算法的思想来源于物理退火原理：

加温时体内部粒子随着温度的升高而变为无序状态，内能增大，而徐徐冷却时粒子渐趋有序，如
果降温速度足够慢，那么在每个溫度下，粒子都可以达到一个平衡态，最后在常温时达到基态，内能减少到最小。

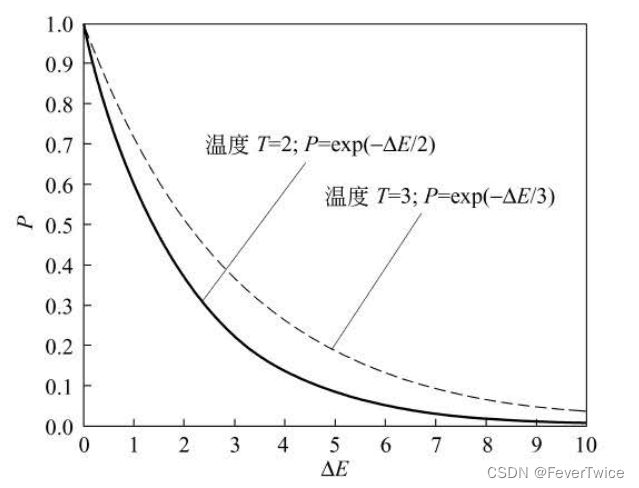
粒子在某个温度时，固体所处的状态具有 定的随机性，而这些状态之间的转换能否实现由 Metropolis 准则决定。公式如下所示：

$$P_{ij}^T=\{\begin{array}{ll}1,& E(j)⩽E(i)\\ {\mathrm{e}}^{-\left(\frac{E(j)-E(i)}{KT}\right)}={\mathrm{e}}^{-\left(\frac{\Delta E}{KT}\right),}& \text{ 其他 }\end{array}$$

如果变化是朝着减少系统能量的方向进行的，那么就接受该变化，否则以一定的概率接受这种变化（指方向变化往能量大的方向进行）

随着温度的降低，能量增加的状态将变得更难被接受

概念对照

退火过程	模拟退火算法
物体内部的状态	问题的解空间（所有可行解）
状态的能量	解的质量（适应度函数值）
温度	控制参数
熔解过程	设定初始温度
退火冷却过程	控制参数的修改（温度参数的下降）
状态的转移	解在邻域中的变化
能量最低状态	最优解

2. 算法基本流程

算法流程图

伪代码

／／功能 模拟退火算法伪代码
／／说明 本例以求问题最小 为目标
／／参数 为初始温度 为内层循环次数
procedure SA 
	//Initialization 
	Randomly generate a soluti on Xi, and calculate its fitness value f(x_0);
	X_best = O; k= 0; t_k = T; 
	while not st op 
		// The search loop under the temperature t_k 
		for i = 1 to L: // The l oop times 
			Generate a new solution X_new, based on the current solution X_k, 
			and calculate its fitness value f(X_new) 
			if f(X_new)< f(X_k) 
				X_k = X_new;
				if(Xk) < (X_best) X_best = Xk;
				continues; 
			end if 
			CalculateP(tk) = exp((f(X_new) - f(X_k)) / (t * K)) ; 
			if random(O, 1) < P 
				X_k= X_new;
			end if 
		end for 
		// Drop down the temperature 
		t_(k+1) = drop (t_k);
		k = k + 1; 
		end while 
	print X_best 
end procedure

---

从流程图中可以看到模拟退火具有两层循环,内循环模拟的是在给定的温度下系统达到热平衡的过程。在该循环中,每次都从当前解 $i$ 的邻域中随机找出一个新解 $j$, 然后按照 Metropolis 准则概率地接受新解。

算法中的 $\mathrm{random}(0,1)$ 是指在区间 $[0,1]$ 上按均匀分 布产生一个随机数, 而所谓的内层达到热平衡也是一个䈼统的说法, 可以定义为循环一定的代数, 或者基于接受率定义平衡等。

算法的外层循环是一个降温的过程, 当在一个温度 下达到平衡后, 开始外层的降温,然后在新的温度下重新开始内循环。降温的方法可以根 据具体问題具体设计, 而且算法流程图中给出的初始温度 $T$ 也需要算法的使用者根据具 体的问题而制定。

2.1 初始温度

初温越大，获得高质量解的几率越大，但花费的计算时间将越多

• 均匀抽样一组状态, 以各状态目标值的方差为初溫;
• 随机产生一组状态, 确定两两状态间的最大目标值差 $|\Delta \max |$, 然后依据差值, 利 用一定的函数确定初温。例如, $t_0=-\Delta \max /p_r$, 其中 $p_r$ 为初始接受概率;
• 利用经验公式给出初始温度。

2.2 领域函数

邻域函数（状态产生函数）应尽可能保证产生的候选解遍布全部解空间，通常由两部分组成，即 生候选解的方式和候选解产生的概率分布

2.3 接收概率

从一个状态 $X_k$ (一个可行解) 向另一个状态 $X_{\text{new }}$ (另一个可行解)的转移概率
它与当前的温度参数 $t_k$ 有关, 随温度下降而减小。

指从某一较高温状态 $t_0$ 向较低温状态冷却时的降温管理表, 或者说降温方式。假设时刻 $k$ 的温度用 $t_k$ 来表示, 则经典模拟退火算法的降温方式为
$$t_k=\frac{t_0}{\lg (1+k)}$$
而快速模拟退火算法的降温方式为 :
$$t_k=\frac{t_0}{1+k}$$
这两种方式都能够使得模拟䢐火算法收敛于全局最小点。

2.4 内层平衡

内层平衡也称 Metropolis 抽样稳定准则，用于决定在各温度下产生候选解的数目

2.5 终止条件

算法终止准则, 常用的包括以下儿项。

• 设置终止温度的阈値；
• 设置外循环迭代次数;
• 算法搜索到的最优值连续若干步保持不变;
• 检验系统熵是否稳定。

---

写在最后

各位看官，都看到这里了，麻烦动动手指头给博主来个点赞8，您的支持作者最大的创作动力哟！
才疏学浅，若有纰漏，恳请斧正
本文章仅用于各位作为学习交流之用，不作任何商业用途，若涉及版权问题请速与作者联系，望悉知