机器学习-有监督学习-集成学习方法(五)：Bootstrap-＞Boosting(提升)方法-＞eXtremeGradientBoosting算法--+决策树--＞XGBoost提升树

一、Bootstrap

Boostrap是靴子的带子的意思，名字来源于“pull up your ownboostraps”，意思是通过拉靴子提高自己，本来的意思是不可能发生的事情，但后来发展成通过自己的努力让事情变得更好。放在组合分类器这里，意思就是通过分类器自己提高分类的性能。
Boostrap只是提供了一种组合方法的思想，就是将基分类器的训练结果进行综合分析，而其它的名称如Bagging、Boosting是对组合方法的具体演绎。

Boostrap组合方法分为：Bagging算法与Boosting算法。

• Bagging的作用：降低“方差”；
• Boost的作用：降低“偏差”；

二、Boosting(提升)

• Boosting由弱分类器得到强分类器的过程：迭代优化：样本加权系数、分类器加权系数；
• Boosting(提升)：是一个迭代的过程，用来自适应的改变训练样本的分布，使分类器聚焦在那些很难分的样本上；
• Boosting(提升)：是一个机器学习技术，可以用于回归和分类问题，它每一步产生个弱预测模型 (如决策树)，并加权累到总模型中。如果每一步的弱预测生成都是依据损失函数的梯度方向，则称之为梯度提升(Gradient boosting)；
• 梯度提升(Gradient boosting) 算法：首先给定 一个目标损失函数，它的定义域是所有可行的弱函数集合(基函数)；提升算法通过迭代地选择一个负梯度方向上的基函数来逐渐逼近局部极小值 。这种在函数域的梯度提升观点对机器学习的很多领域有深刻影响；
• Boosting(提升)的理论意义：如果一个问题存在弱分类器，则可以通过提升的办法得到强分类器；
• 以决策树(分类树、回归树)为基学习器的提升(boosting)方法称为提升树(Boosting tree)。
• 对于Boosting，每一步我们都会在上一轮的基础上更加拟合原数据，总体上实现了整体模型的偏差(bias)最小化。所以对于每个基分类器来说，首要任务就是如何降低方差(variance)，即选择更简单的分类器，所以我们采用深度很浅的决策树。

三、Boosting(提升)算法的理论基础

• Boosting(提升)算法：给定输入向量 $\text{x}$ 和输出变量 $y$ 组成的若干训练样本$D=\{({\text{x}}_1,y_1),({\text{x}}_2,y_2),\dots ,({\text{x}}_n,y_n)\}$，
• 目标是找到一个近似函数 $\hat{F}(\text{x})={\sum }_{m=1}^M{\alpha }_m{h}_m(\text{x})$，其中：系数 ${\alpha }_m$ 为各个弱学习器的权重，$h_m(\text{x})$ 为弱学习器，$m=1,2,...,M$ ，使得损失函数 $L(\text{y},\hat{F}(\text{x}))$ 最小。

四、XGBoost(eXtreme Gradient Boosting 极端梯度提升)

• XGBoost，在计算速度和准确率上，较GBDT有明显的提升。xgboost 的全称是eXtreme Gradient Boosting，它是Gradient Boosting Machine的一个c++实现，作者为正在华盛顿大学研究机器学习的大牛陈天奇 。
• XGBoost最大的特点在于，它能够自动利用CPU的多线程进行并行，同时在算法上加以改进提高了精度。它的处女秀是Kaggle的 希格斯子信号识别竞赛，因为出众的效率与较高的预测准确度在比赛论坛中引起了参赛选手的广泛关注。
• 一般地说， XGBoost 的速度和性能优于 sklearn.ensemble.GradientBoostingClassifier类
• 作为GBDT的高效实现，XGBoost是一个上限特别高的算法，因此在算法竞赛中比较受欢迎。简单来说，对比原算法GBDT，XGBoost主要从下面三个方面做了优化：
  1. 一是算法本身的优化：在算法的弱学习器模型选择上，对比GBDT只支持决策树，还可以直接很多其他的弱学习器。在算法的损失函数上，除了本身的损失，还加上了正则化部分。在算法的优化方式上，GBDT的损失函数只对误差部分做负梯度（一阶泰勒）展开，而XGBoost损失函数对误差部分做二阶泰勒展开，更加准确。算法本身的优化是我们后面讨论的重点。
  2. 二是算法运行效率的优化：对每个弱学习器，比如决策树建立的过程做并行选择，找到合适的子树分裂特征和特征值。在并行选择之前，先对所有的特征的值进行排序分组，方便前面说的并行选择。对分组的特征，选择合适的分组大小，使用CPU缓存进行读取加速。将各个分组保存到多个硬盘以提高IO速度。
  3. 三是算法健壮性的优化：对于缺失值的特征，通过枚举所有缺失值在当前节点是进入左子树还是右子树来决定缺失值的处理方式。算法本身加入了L1和L2正则化项，可以防止过拟合，泛化能力更强。

1、XGBoost 的优势

• Regularization：
  • 标准的GBM并没有XGBoost的Regularization，这个能帮助减少过拟合问题
• Parallel Processing:
  • XGBoost实现了并行计算，与GBM相比非常快
  • 但是基于序列的模型，新模型的建立是基于前面已经建立好的模型，如何能实现并行计算呢？探索一下吧
  • XGBoost 支持在Hadoop上实现
• High Flexibility
  • XGBoost允许用户定制优化目标和评价标准
  • 这一点将会使得我们对模型有很多可以改进的地方
• Handling Missing Values
  • XGBoost有内嵌的处理缺失值的程序
  • 其他模型中用户被要求为缺失值提供相应的与其他值不同的值去填充缺失值，XGBoost会尝试对缺失值进行分类，并学习这种分类
• Tree Pruning:
  • GBM会停止对一个节点进行分裂，当其计算到这个节点的split的loss是负数时，GBM是一个贪婪算法
  • XGBoost的分类取决于max_depth，当树的深度达到max_depth时，开始进行剪枝，移除没有正基尼（no positive gain）节点的split
  • 另一个优点是一个节点被分裂的时候loss为-2，当其二次分裂的时候loss可能为+10，GBM会停止该节点的分裂，XGBoost会进入到第二步，然后结合两个分裂的影响，最终为+8
• Built-in Cross-Validation
  • XGBoost允许每一个交叉验证实现boosting过程，因而通过一次run就能获得boosting迭代的优化量
  • 与GBM需要运营grid-search且需要限时值的范围获得优化量不同
• Continue on Existing Model
• 用户可以通过上个版本的XGBoost模型训练新版本的模型
• GBM的sklearn也有这个特性

2、XGBoost损失函数

在看XGBoost本身的优化内容前，我们先回顾下GBDT的回归算法迭代的流程，对于GBDT的第 $t$ 颗决策树，主要是走下面5步：

1. 第 $t$ 轮（第 $t$ 棵决策树）的第 $i$ 个样本的损失函数的负梯度函数表示为
   $$r_i^{(t)}=-{\left[\frac{\partial L(y_i,F({\text{x}}_i))}{\partial F({\text{x}}_i)}\right]}_{F({\text{x}}_i)=F_{t-1}({\text{x}}_i)}$$
   
2. 利用 $({\text{x}}_i,r_i^{(t)})(i=1,2,..m)$，我们可以拟合一颗CART回归树，得到了第 $t$ 颗回归树，其对应的叶节点区域 $R_j^{(t)},j=1,2,...,J$。其中 $J$ 为叶子节点的个数。
3. 针对每一个叶子节点里的样本，我们求出使损失函数最小，也就是拟合叶子节点最好的的输出值 $c_j^{(t)}$ 如下，其中c为随机初始化的值：
   $$c_j^{(t)}=\underset{c}{argmin}\sum _{{\text{x}}_i\in R_j^{(t)}}L(y_i,F_{t-1}({\text{x}}_i)+c)$$
4. 这样我们就得到了本轮的决策树拟合函数如下：
   $$h^{(t)}(\text{x})=\sum _{j=1}^J{c}_j^{(t)}I(x\in R_j^{(t)})$$
5. 更新强学习器
   $$F_t(\text{x})=F_{t-1}(\text{x})+h^{(t)}(\text{x})$$

上面第一步是得到负梯度，或者是泰勒展开式的一阶导数。第二步是第一个优化求解，即基于残差拟合一颗CART回归树，得到 $J$ 个叶子节点区域。第三步是第二个优化求解，在第二步优化求解的结果上，对每个节点区域再做一次线性搜索，得到每个叶子节点区域的最优取值。最终得到当前轮的强学习器。

从上面可以看出，我们要求解这个问题，需要求解当前决策树最优的所有 $J$ 个叶子节点区域和每个叶子节点区域的最优解 $c_j^{(t)}$。GBDT采样的方法是分两步走，先求出最优的所有 $J$ 个叶子节点区域，再求出每个叶子节点区域的最优解。

对于XGBoost，它期望把第2步和第3步合并在一起做，即一次求解出决策树最优的所有 $J$ 个叶子节点区域和每个叶子节点区域的最优解$c_j^{(t)}$。

在讨论如何求解前，我们先看看XGBoost的损失函数的形式，在GBDT损失函数 $L(y,F_t(\text{x}))=L(y,F_{t-1}(\text{x})+h_t(\text{x}))$ 的基础上，我们加入正则化项如下：

$$\Omega (h_t)=\gamma J+\frac{\lambda }{2}\sum _{j=1}^J{w}_{tj}^2$$

这里的 $J$ 是叶子节点的个数，而 $w_{tj}$ 是第 $j$ 个叶子节点的最优值。这里的 $w_{tj}$ 和我们GBDT里使用的 $c_{tj}$ 是一个意思，只是XGBoost的论文里用的是 $w$ 表示叶子区域的值，因此这里和论文保持一致。

最终XGBoost的损失函数可以表达为：

$$L_t=\sum _{i=1}^{m}L(y_i,f_{t-1}(x_i)+h_t(x_i))+\gamma J+\frac{\lambda }{2}\sum _{j=1}^J{w}_{tj}^2$$

最终我们要极小化上面这个损失函数，得到第 $t$ 个决策树最优的所有 $J$ 个叶子节点区域和每个叶子节点区域的最优解 $w_{tj}$。XGBoost没有和GBDT一样去拟合泰勒展开式的一阶导数，而是期望直接基于损失函数的二阶泰勒展开式来求解。

现在我们来看看这个损失函数的二阶泰勒展开式：

$$\begin{array}{rl}{L}_t& =\sum _{i=1}^{m}L(y_i,f_{t-1}(x_i)+h_t(x_i))+\gamma J+\frac{\lambda }{2}\sum _{j=1}^J{w}_{tj}^2\\ & \approx \sum _{i=1}^m(L(y_i,f_{t-1}(x_i))+\frac{\partial L(y_i,f_{t-1}(x_i)}{\partial f_{t-1}(x_i)}{h}_t(x_i)+\frac{1}{2}\frac{{\partial }^{2}L(y_i,f_{t-1}(x_i)}{\partial f_{t-1}^2(x_i)}{h}_t^2(x_i))+\gamma J+\frac{\lambda }{2}\sum _{j=1}^J{w}_{tj}^2\end{array}$$

为了方便，我们把第i个样本在第t个弱学习器的一阶和二阶导数分别记为：

$$g_{ti}=\frac{\partial L(y_i,f_{t-1}(x_i)}{\partial f_{t-1}(x_i)},h_{ti}=\frac{{\partial }^{2}L(y_i,f_{t-1}(x_i)}{\partial f_{t-1}^2(x_i)}$$

则我们的损失函数现在可以表达为：

$$L_t\approx \sum _{i=1}^m(L(y_i,f_{t-1}(x_i))+g_{ti}{h}_t(x_i)+\frac{1}{2}{h}_{ti}{h}_t^2(x_i))+\gamma J+\frac{\lambda }{2}\sum _{j=1}^J{w}_{tj}^2$$

损失函数里面 $L(y_i,f_{t-1}(x_i))$是常数，对最小化无影响，可以去掉，同时由于每个决策树的第 $j$ 个叶子节点的取值最终会是同一个值$w_{tj}$，因此我们的损失函数可以继续化简。

$$\begin{array}{rl}{L}_t& \approx \sum _{i=1}^m[g_{ti}{h}_t(x_i)+\frac{1}{2}{h}_{ti}{h}_t^2(x_i)]+\gamma J+\frac{\lambda }{2}\sum _{j=1}^J{w}_{tj}^2\\ & =\sum _{j=1}^J(\sum _{x_i\in R_{tj}}{g}_{ti}{w}_{tj}+\frac{1}{2}\sum _{x_i\in R_{tj}}{h}_{ti}{w}_{tj}^2)+\gamma J+\frac{\lambda }{2}\sum _{j=1}^J{w}_{tj}^2\\ & =\sum _{j=1}^J[(\sum _{x_i\in R_{tj}}{g}_{ti})w_{tj}+\frac{1}{2}(\sum _{x_i\in R_{tj}}{h}_{ti}+\lambda )w_{tj}^2]+\gamma J\end{array}$$

我们把每个叶子节点区域样本的一阶和二阶导数的和单独表示如下：

$$G_{tj}=\sum _{x_i\in R_{tj}}{g}_{ti},H_{tj}=\sum _{x_i\in R_{tj}}{h}_{ti}$$

最终损失函数的形式可以表示为：

$$L_t=\sum _{j=1}^J[G_{tj}{w}_{tj}+\frac{1}{2}(H_{tj}+\lambda )w_{tj}^2]+\gamma J$$

现在我们得到了最终的损失函数，那么回到前面讲到的问题，我们如何一次求解出决策树最优的所有 $J$ 个叶子节点区域和每个叶子节点区域的最优解 $w_{tj}$ 呢？

3、XGBoost损失函数的优化求解

关于如何一次求解出决策树最优的所有 $J$ 个叶子节点区域和每个叶子节点区域的最优解 $w_{tj}$，我们可以把它拆分成2个问题：

1. 如果我们已经求出了第 $t$ 个决策树的 $J$ 个最优的叶子节点区域，如何求出每个叶子节点区域的最优解 $w_{tj}$？
2. 对当前决策树做子树分裂决策时，应该如何选择哪个特征和特征值进行分裂，使最终我们的损失函数 $L_t$ 最小？

对于第一个问题，其实是比较简单的，我们直接基于损失函数对 $w_{tj}$ 求导并令导数为0即可。这样我们得到叶子节点区域的最优解 $w_{tj}$ 表达式为：

$$w_{tj}=-\frac{G_{tj}}{H_{tj}+\lambda }$$

我们已经解决了第一个问题。现在来看XGBoost优化拆分出的第二个问题：如何选择哪个特征和特征值进行分裂，使最终我们的损失函数 $L_t$ 最小？

在GBDT里面，我们是直接拟合的CART回归树，所以树节点分裂使用的是均方误差。XGBoost这里不使用均方误差，而是使用贪心法，即每次分裂都期望最小化我们的损失函数的误差。

注意到在我们 $w_{tj}$ 取最优解的时候，原损失函数对应的表达式为：

$$L_t=-\frac{1}{2}\sum _{j=1}^J\frac{G_{tj}^2}{H_{tj}+\lambda }+\gamma J$$

如果我们每次做左右子树分裂时，可以最大程度的减少损失函数的损失就最好了。也就是说，假设当前节点左右子树的一阶二阶导数和为 $G_L$,$H_L$,$G_R$,$H_L$, 则我们期望最大化下式：

$$-\frac{1}{2}\frac{(G_L+G_R{)}^2}{H_L+H_R+\lambda }+\gamma J-(-\frac{1}{2}\frac{G_L^2}{H_L+\lambda }-\frac{1}{2}\frac{G_R^2}{H_R+\lambda }+\gamma (J+1))$$

整理下上式后，我们期望最大化的是：

$$\frac{1}{2}\frac{G_L^2}{H_L+\lambda }+\frac{1}{2}\frac{G_R^2}{H_R+\lambda }-\frac{1}{2}\frac{(G_L+G_R{)}^2}{H_L+H_R+\lambda }-\gamma$$

也就是说，我们的决策树分裂标准不再使用CART回归树的均方误差，而是上式了。

具体如何分裂呢？举个简单的年龄特征的例子如下，假设我们选择年龄这个 特征的值 $a$ 作为决策树的分裂标准，则可以得到左子树2个人，右子树三个人，这样可以分别计算出左右子树的一阶和二阶导数和，进而求出最终的上式的值。

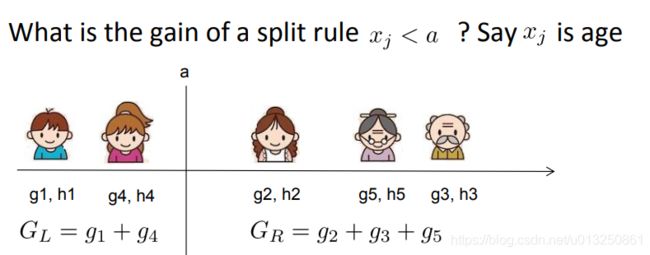
然后我们使用其他的不是值 $a$ 的划分标准，可以得到其他组合的一阶和二阶导数和，进而求出上式的值。最终我们找出可以使上式最大的组合，以它对应的特征值来分裂子树。

至此，我们解决了XGBoost的2个优化子问题的求解方法。

4、XGBoost算法主流程

这里我们总结下XGBoost的算法主流程，基于决策树弱分类器。不涉及运行效率的优化和健壮性优化的内容。

• 输入是训练集样本 $I=\{(x_{,}{y}_1),(x_2,y_2),...(x_m,y_m)\}$， 最大迭代次数 $T$, 损失函数 $L$， 正则化系数 $\lambda ,\gamma$。

• 输出是强学习器 $f(x)$

• 对迭代轮数 t=1,2,…T 有：

  1. 计算第 $i$ 个样本 (i-1,2,…m) 在当前轮损失函数 $L$ 基于 $f_{t-1}(x_i)$ 的一阶导数 $g_{ti}$，二阶导数 $h_{ti}$,计算所有样本的一阶导数和 $G_t=\sum _{i=1}^m{g}_{ti}$,二阶导数和 $H_t=\sum _{i=1}^m{h}_{ti}$
  2. 基于当前节点尝试分裂决策树，默认分数score=0，G和H为当前需要分裂的节点的一阶二阶导数之和。
     对特征序号 k=1,2…K:
     a) $G_L=0,H_L=0$
     b.1) 将样本按特征k从小到大排列，依次取出第i个样本，依次计算当前样本放入左子树后，左右子树一阶和二阶导数和：$$G_L=G_L+g_{ti},G_R=G-G_L$$$$H_L=H_L+h_{ti},H_R=H-H_L$$
     b.2) 尝试更新最大的分数：$$score=max(score,\frac{1}{2}\frac{G_L^2}{H_L+\lambda }+\frac{1}{2}\frac{G_R^2}{H_R+\lambda }-\frac{1}{2}\frac{(G_L+G_R{)}^2}{H_L+H_R+\lambda }-\gamma )$$
  3. 基于最大score对应的划分特征和特征值分裂子树。
  4. 如果最大score为0，则当前决策树建立完毕，计算所有叶子区域的$w_{tj}$, 得到弱学习器$h_t(x)$，更新强学习器$f_t(x)$,进入下一轮弱学习器迭代.如果最大score不是0，则转到第2)步继续尝试分裂决策树。

5、XGBoost算法运行效率的优化

在第2,3,4节我们重点讨论了XGBoost算法本身的优化，在这里我们再来看看XGBoost算法运行效率的优化。

大家知道,Boosting算法的弱学习器是没法并行迭代的，但是单个弱学习器里面最耗时的是决策树的分裂过程，XGBoost针对这个分裂做了比较大的并行优化。对于不同的特征的特征划分点，XGBoost分别在不同的线程中并行选择分裂的最大增益。

同时，对训练的每个特征排序并且以块的的结构存储在内存中，方便后面迭代重复使用，减少计算量。计算量的减少参见上面第4节的算法流程，首先默认所有的样本都在右子树，然后从小到大迭代，依次放入左子树，并寻找最优的分裂点。这样做可以减少很多不必要的比较。

具体的过程如下图所示：

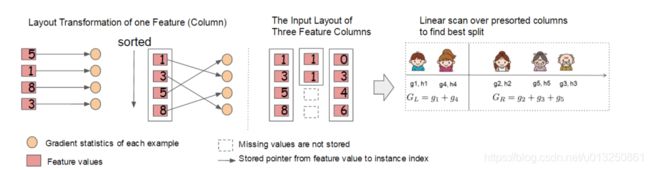
　此外，通过设置合理的分块的大小，充分利用了CPU缓存进行读取加速（cache-aware access）。使得数据读取的速度更快。另外，通过将分块进行压缩（block compressoin）并存储到硬盘上，并且通过将分块分区到多个硬盘上实现了更大的IO。

6、XGBoost算法健壮性的优化

最后我们再来看看XGBoost在算法健壮性的优化，除了上面讲到的正则化项提高算法的泛化能力外，XGBoost还对特征的缺失值做了处理。

XGBoost没有假设缺失值一定进入左子树还是右子树，则是尝试通过枚举所有缺失值在当前节点是进入左子树，还是进入右子树更优来决定一个处理缺失值默认的方向，这样处理起来更加的灵活和合理。

也就是说，上面第4节的算法的步骤a),b.1)和b.2)会执行2次，第一次假设特征k所有有缺失值的样本都走左子树，第二次假设特征k所有缺失值的样本都走右子树。然后每次都是针对没有缺失值的特征k的样本走上述流程，而不是所有的的样本。

如果是所有的缺失值走右子树，使用上面第4节的a),b.1)和b.2)即可。如果是所有的样本走左子树，则上面第4节的a)步要变成：

$$G_R=0,H_R=0$$

b.1)步要更新为：$$G_R=G_R+g_{ti},G_L=G-G_R$$$$H_R=H_R+h_{ti},H_L=H-H_R$$

7、XGBoost小结

不考虑深度学习，则XGBoost是算法竞赛中最热门的算法，它将GBDT的优化走向了一个极致。当然，后续微软又出了LightGBM，在内存占用和运行速度上又做了不少优化，但是从算法本身来说，优化点则并没有XGBoost多。

何时使用XGBoost，何时使用LightGBM呢？个人建议是优先选择XGBoost，毕竟调优经验比较多一些，可以参考的资料也多一些。如果你使用XGBoost遇到的内存占用或者运行速度问题，那么尝试LightGBM是个不错的选择。

五、XGBoost算法调参

当模型没有达到预期效果的时候，XGBoost就是数据科学家的最终武器。XGboost是一个高度复杂的算法，有足够的能力去学习数据的各种各样的不规则特征。

用XGBoost建模很简单，但是提升XGBoost的模型效果却需要很多的努力。因为这个算法使用了多维的参数。为了提升模型效果，调参就不可避免，但是想要知道参数怎么调，什么样的参数能够得出较优的模型输出就很困难了。

XGBoost的变量类型有三类：

• General Parameters：调控整个方程
• Booster Parameters：调控每步树的相关变量
• Learning Task Parameters：调控优化表现的变量

1、General Parameters

• booster [default=gbtree]：
  • gbtree: tree-based models，树模型
  • gblinear: linear models，线性模型
• silent [default=0]:
  • 设置成1表示打印运行过程中的相关信息
  • 通常选择默认值就好，打印出的信息能够帮助理解model
• nthread [default to maximum number of threads available if not set]
  • 主要用于并行计算，系统的内核数需要作为变量
  • 如果希望运行所有的内核，就不需要设置该参数，程序会自己检测到该值

2、Booster Parameters

虽然XGBoost有两种boosters,作者在参数这一块只讨论了tree booster，原因是tree booster的表现总是好于 linear booster

• eta [default=0.3]
  • 与GBM中学习率的概念相似
  • 通过减小每一步的权重能够使得建立的模型更鲁棒
  • 通常最终的数值范围在[0.01-0.2]之间
• min_child_weight [default=1]
  • 定义观测样本生成的孩子节点的权重最小和
  • 这个概念与GBM中的min_child_leaf概念类似，但是又不完全一样，这个概念指的是某观测叶子节点中所有样本权重之和的最小值，而GBM指的是叶子节点的最少样本量
  • 用于防止过拟合问题：较大的值能防止过拟合，过大的值会导致欠拟合问题
  • 需要通过CV调参
• max_depth [default=6]
  • 树的最大深度
  • 用于防止过拟合问题
  • 通过CV调参
  • 通常值的范围：[3-10]
• max_leaf_nodes
  • 一棵树最多的叶子节点的数目
  • 与max_depth定义一个就好
• gamma [default=0]
  • 一个节点分裂的条件是其分裂能够起到降低loss function的作用，gamma 定义loss function降低多少才分裂
  • 这个变量使得算法变得保守，它的值取决于 loss function需要被调节
• max_delta_step [default=0]
  • 此变量的设置使得我们定义每棵树的权重估计值的变化幅度。如果值为0，值的变化没有限制，如果值>0，权重的变化将会变得相对保守
  • 通常这个参数不会被使用，但如果是极度不平衡的逻辑回归将会有所帮助
• subsample [default=1]：
  • 与GBM的subsample定义一样，指的是没有每棵树的样本比例
  • 低值使得模型更保守且能防止过拟合，但太低的值会导致欠拟合
  • 通常取值范围[0.5-1]
• colsample_bytree [default=1]
  • 与GBM中的max_features类似，指的是每棵树随机选取的特征的比例
  • 通常取值范围[0.5-1]
• colsample_bylevel [default=1]
  • 指的是树的每个层级分裂时子样本的特征所占的比例
  • 作者表示不用这个参数，因为subsample和colsample_bytree组合做的事与之类似
• lambda [default=1]
  • L2正则化权重的术语（同 Ridge regression）
  • 用于处理XGBoost里的正则化部分，虽然很多数据科学家不怎么使用这个参数，但是它可以用于帮助防止过拟合
• alpha [default=0]
  • L1正则化的权重术语（同Lasso regression）
  • 当特征量特别多的时候可以使用，这样能加快算法的运行效率
• scale_pos_weight [default=1]
  • 当样本不平衡时，需要设置一个大于0的数帮助算法尽快收敛

3、Learning Task Parameters

此类变量用于定义优化目标每一次计算的需要用到的变量

• objective [default=reg:linear]
  • 用于定义loss function，通常有以下几类
  • binary:logistic-用于二分类，返回分类的概率而不是类别（class）
  • multi:softmax-多分类问题，返回分类的类别而不是概率
  • multi:softprob-与softmax类似，但是返回样本属于每一类的概率
• eval_metric [ default according to objective ]
  • 这个变量用于 测试数据（validation data.）
  • 默认值：回归-rmse；分类-error
  • 通常值如下：
    • rmse – root mean square error
    • mae – mean absolute error
    • logloss – negative log-likelihood
    • error – Binary classification error rate (0.5 threshold)
    • merror – Multiclass classification error rate
    • mlogloss – Multiclass logloss
    • auc: Area under the curve
• seed [default=0]
  • 随机种子的值

有些变量在Python的sklearn的接口中对应命名如下：

1. eta -> learning rate
2. lambda ->reg_lambda
3. alpha -> reg_alpha

可能感到困惑的是这里并没有像GBM中一样提及n_estimators，这个参数实际存在于XGBClassifier中，但实际是通过num_boosting_rounds在我们调用fit函数事来体现的。

六、GBDT和XGBoost的区别

• 传统GBDT以CART作为基分类器，xgboost还支持线性分类器，这个时候xgboost相当于带L1和L2正则化项的逻辑斯蒂回归（分类问题）或者线性回归（回归问题）。
• 传统GBDT在优化时只用到一阶导数信息，xgboost则对代价函数进行了二阶泰勒展开，同时用到了一阶和二阶导数。顺便提一下，xgboost工具支持自定义代价函数，只要函数可一阶和二阶求导。
• xgboost在代价函数里加入了正则项，用于控制模型的复杂度。正则项里包含了树的叶子节点个数、每个叶子节点上输出的score的L2模的平方和。从Bias-variance tradeoff角度来讲，正则项降低了模型的variance，使学习出来的模型更加简单，防止过拟合，这也是xgboost优于传统GBDT的一个特性。
• Shrinkage（缩减），相当于学习速率（xgboost中的eta）。xgboost在进行完一次迭代后，会将叶子节点的权重乘上该系数，主要是为了削弱每棵树的影响，让后面有更大的学习空间。实际应用中，一般把eta设置得小一点，然后迭代次数设置得大一点。（补充：传统GBDT的实现也有学习速率）
• 列抽样（column subsampling）。xgboost借鉴了随机森林的做法，支持列抽样，不仅能降低过拟合，还能减少计算，这也是xgboost异于传统gbdt的一个特性。
• 对缺失值的处理。对于特征的值有缺失的样本，xgboost可以自动学习出它的分裂方向。
• xgboost工具支持并行。boosting不是一种串行的结构吗?怎么并行的？注意xgboost的并行不是tree粒度的并行，xgboost也是一次迭代完才能进行下一次迭代的（第t次迭代的代价函数里包含了前面t-1次迭代的预测值）。xgboost的并行是在特征粒度上的。我们知道，决策树的学习最耗时的一个步骤就是对特征的值进行排序（因为要确定最佳分割点），xgboost在训练之前，预先对数据进行了排序，然后保存为block结构，后面的迭代中重复地使用这个结构，大大减小计算量。这个block结构也使得并行成为了可能，在进行节点的分裂时，需要计算每个特征的增益，最终选增益最大的那个特征去做分裂，那么各个特征的增益计算就可以开多线程进行。
• 可并行的近似直方图算法。树节点在进行分裂时，我们需要计算每个特征的每个分割点对应的增益，即用贪心法枚举所有可能的分割点。当数据无法一次载入内存或者在分布式情况下，贪心算法效率就会变得很低，所以xgboost还提出了一种可并行的近似直方图算法，用于高效地生成候选的分割点。

七、XGBoost 样本不平衡问题

何谓样本不平衡——简单来说就是数据集中负样本的数量远远大于正样本的数量。在这个情况下，模型就会倾向于把样本预测为负样本，因为这是最便捷的降低损失、提高模型准确率的方法。例如：有一个正样本数量为1，负样本数量为99的数据集，模型就算无脑地把全部样本预测为负样本也能达到99%的准确度，试想有这么一个分类器，每次我们把数据喂‘给它时，在不调整阈值的情况下，它都倾向于把测试集的样本预测为负样本，你觉得这样的分类器还会是一个好的分类器吗？

在对不平衡数据进行训练时，通常会考虑一下怎么处理不平衡数据能使训练出来的结果较好。

在用xgboost训练二分类模型时，除了直接使用过采样和下采样，xgboost接口还提供一些处理不平衡数据的方法，有scale_pos_weight参数的设置，还有给样本赋予一定的权重。

---

---

---

梯度提升树(GBDT)原理小结
XGBoost算法原理小结
XGBoost算法原理
XGBoost算法原理简介及调参01
XGBoost算法原理简介及调参02-Python代码
XGBoost20题
机器学习算法中 GBDT 和 XGBOOST 的区别有哪些？
xgboost是用二阶泰勒展开的优势在哪？
通俗的将Xgboost的原理讲明白
[机器学习] XGBoost 样本不平衡问题
分类案例：XGB中的样本不均衡问题