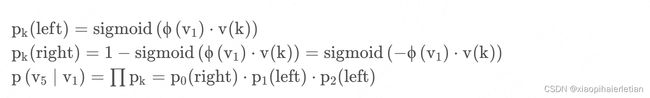Graph Neural Networks (GNN)（五）：Graph Embedding (DeepWalk, Line, Node2Vec)

1. 概述
本系列之前文章主要介绍了基于空间（Spatial）和图谱（Spectral）理论的图神经网络（GNN）
Graph Neural Networks (GNN)（一）：Spatial-GNN
Graph Neural Networks (GNN)（二）：Spectral-GNN 引言和导入
Graph Neural Networks (GNN)（三）：Spectral-GNN 之 GCN
Graph Neural Networks (GNN)（四）：Spectral-GNN 与 Spatial-GNN 对比

以上方法大多用于有监督的任务，通过监督的损失函数来学习神经网络的参数。而这一节介绍的方法主要是无监督的，我们可以认为这一节主要是 Graph Embedding 的方法，通过无监督的方法，将节点向量（例如，引文网络中每个节点有论文中出现的词袋向量）降维到一个低维的特征空间。我们可以将这一步看成降维，也可以看成特征选择和特征提取。然后学到的低维特征（也称为 embedding）可以用于下游任务，例如直接替换原有的特征矩阵用于后续的节点分类任务等。

无监督学习的一个关键问题：如何设计优化的目标函数。因为监督任务的目标函数很容易设计，可以根据分类的交叉熵损失函数来设定，但是由于无监督的，那么如何设计呢？

这一篇博客的方法都是借鉴大名鼎鼎的 Word2Vec 的方法来设计的。Word2Vec 是 NLP 中的方法，那么如何迁移到 Graph 中啊。显然 NLP 中一个句子是线性结构的，但是 Graph 是非线性的。怎么处理这个问题呢？

解决方法：我们在 Graph 上对某一个节点进行随机游走，产生的随机游走类比成一种特殊的语言句子，每个节点类比为一个单词。Word2Vec 根据句子产生出单词的 Embedding，那么这一类方法可以根据随机游走产生节点的 Embedding。进一步，可以根据两个节点的 Embedding 可以得到边的 Embbeding

2. 基础知识：Word2Vec
因为这一篇主要讲的是 Graph Embedding，对这一部分只是简单地介绍思想。

一个单词最初如何表示？ One-Hot 向量，假设词汇表有 10000 个单词，那么某一单词就用一个 10000 维的向量表示，并且只有对应的某一维是 1，其他维度为 0。这种方法缺点很明显：第一就是维度太高，有很多冗余信息；第二就是不能很好的表现单词之间的相似性等关系。

Word2Vec 目的就是降维，并且可以保留单词的信息。怎么降维呢？

我们看下面两个句子：

我的篮球偶像是科比
我的篮球偶像是詹姆斯
我们容易知道科比和詹姆斯是相似的词汇，因为 Embedding 之后在 Embedding 空间中是接近的。我们可以在爬取很多这样句子（例如你可以找文学著作战争与和平），然后使用其中出现的句子来学习这个 Embedding Function。

语言模型需要计算出一句话在词袋空间中出现的概率，通常的优化目标是最大化概率。w 表示词袋中的单词，序号表示了词在句子中的顺序关系，但是这个目标实现起来比较困难。

下一个问题是如何建模这种想法呢？常见方式有两种：

Continuous bag of word ( CBOW )：简单的说就是给定一个单词的上下文，来预测出现某一词的概率。例如：我喜欢在__打篮球。根据前面的“我喜欢在”和后面的“打篮球”去预测中间出现的单词，显然“周末”、“操场”之类的概率打。
Skip-gram：简单说就是给定一个单词预测上下文的概率。例如：_在周末。根据在周末预测前后上下文，显然后面“逛街”、“打篮球”的概率较高。
由于我见过的大部分模型使用的都是 Skip-Gram，这里多讲一下：Skip-Gram放宽了限制，做了一些调整。参考Graph embedding: 从Word2vec到DeepWalk

不再用句子中前面的词来预测下一个词，而是用当前词去预测句子中周围的词；
周围的词包括当前词的左右两侧的词；
丢掉了词序信息，并且在预测周围词的时候，不考虑与当前词的距离。优化目标是最大化同一个句子中同时出现的词的共现概率 ，其中 k 是滑动窗口大小。
Skip-Gram的模型结构如下图所示，在整个词袋 vocabulary 中预测上下文词，在输出端需要做一个 |V| 维度的分类，|V| 表示词袋 vocabulary 中词的数量。每一次迭代计算量非常庞大，这是不可行的。为了解决这个问题，采用了 Hierarchical Softmax 分类算法。

 

 Hierarchical Softmax: 如下图所示，构建一个二叉树，每一个词或者分类结果都分布在二叉树的叶子节点上，在做实际分类的时候，从根节点一直走到对应的叶子节点，在每一个节点都做一个二分类。假设这是一颗均衡二叉树，并且词袋的大小是|V|，那么从根走到叶子节点只需要进行 次计算，远远小于 |V| 的计算量。

具体如何计算？我们以上图中用预测 为例进行介绍。树的根部输入的是的向量，用表示。在二叉树的每一个节点上都存放一个向量，需要通过学习得到，最后的叶子节点上没有向量。显而易见，整棵树共有 |V| 个向量。规定在第k层的节点做分类时，节点左子树为正类别，节点右子树是负类别，该节点的向量用v ( k ) 表示。那么正负类的分数如下公式所示。在预测的时候，需要按照蓝色箭头的方向做分类，第0层分类结果是负类，第1层分类结果是正类，第2层分类结果是正类，最后到达叶子节点。最后把所有节点的分类分数累乘起来，作为预测的概率，如下面公式所示，并通过反向传播进行优化。

 接下来看看一个实际例子理解 Skip-Gram

 如图所示，某一个句子 “The quick brown fox jumps over the lazy dog.”。我们按顺序选在中间词汇，并且设定 window size 为 2 （也就是前后 2 个以内的单词），对于第一个可以得到 (the, quick) 和 (the, brown)，意思就是 the 的上下文中出现过 quick 和 brown，因此对应的概率高，最后 fox 单词前后一共 4 个单词一起出现的概率高。然后可以根据这个构建无监督的损失函数，获得 embedding。

这里只简单介绍思想，后面会有 Deepwalk，Line 和 Node2Vec 的具体损失函数形式和类似的负采样等策略。其实两者都是很类似的，如果你有 NLP 的知识那么看后面三个模型感觉很简单，如果没有，你看了后面三个模型也能类比出 NLP 中如何获取的 Embedding。

3. Graph Embedding
3.1. DeepWalk
DeepWalk: Online Learning of Social Representations

DeepWalk 使用截断的随机游走来为节点学习潜在表示（Embedding），将随机游走视为一种 NLP 中的句子的等价物（将 Graph 看成一种特殊的语言，随机游走看成一种特殊的句子，节点就看成单词，单词的 Embedding 就是节点的 Embedding）。

文中提出了四个学习目标：

适应性：实际的网络是不断变化的，期望学到的表示不需要每次网络变化都要重新学习。
社区意识：潜在空间的两个向量之间的距离应该表示这两个向量对应节点在网络中的某种相似性。（例如，如果是社交网络，属于同一社区的用户在潜在空间的向量应该接近）
低维
连续：连续空间有更光滑的决策边界，且更加鲁棒。
3.1.1 随机游走
代表以 为根节点的随机游走，随机游走是一种马尔科夫链，也就是说随机游走中下一时刻的节点至于当前节点有关，与之前的节点没有关系，即文中的 ，这是以为根节点的随机游走的前 k 个节点，是在的邻居节点中随机选取的。

 以文中图片为例，红色的节点序列就是以某一红色节点为根节点产生的随机序列。更具体的：

 假设以 6 节点为根节点的随机游走（游走长度为 2），可能产生的随机游走序列为：615 626 679 等等。正式地说：可重复访问已访问节点的深度优先遍历算法。这些序列就可以看成是一个句子。。

随机游走有几个很好的特性：

1.局部探索可以容易并行化；显然一个随机游走（一般较短）只采样某个节点的领域，因此可以对多个节点并行化处理。（多线程，多进程，多机器）
2.短的随机游走可以很好适应网络的小变化：例如在大的图中，一个小区域的变化可能不会影响到另一完全不相关的区域的随机游走，因此不用每次网络变化就要重新产生节点的表示。

3.1.2 幂定律
NLP 中单词的频率和随机游走中节点出现的频率有相似的分布：符合幂定律。因此可以使用 NLP 中的方法来建模 Graph。

3.1.3 语言建模：
语言建模的目的是估计语料库中某一特定单词序列出现的概率。

其中代表某个单词，代表词汇表，W 代表的某个句子。

形式化目标函数就是：

这里有个假设：条件独立性假设，上面的 2w 个节点的概率可以看成相互独立的，也就是上面概率可以变为 2w 个概率的乘积。

其中 就是我们的 Embedding Function，本来应该最大化，然后加一个负号就成为了最小。条件概率之前的顶点就是某条随机游走序列中节点前后相连的节点，窗口大小就是 w。

3.1.4 DeepWalk

这里解释一下几个参数的含义：

 w 是窗口大小，d 是 embedding 之后的维度，是每个节点的随机游走序列个数，t 是随机游走长度。

区分一下 w 和 t ：

这个例子中 w = 2 ，t = 10。即这个随机游走长度为 10，然后滑动窗口宽度为 2，即每个单词考虑前后相隔不超过 2 的单词为上下文。

然后就是两个提高效率的方法：负采样和层次 softmax。

总之这个方法可以看成 Word2Vec 的一个 Graph 的变形。Graph Embedding 的开山之作。

3.2. Node2Vec
node2vec: Scalable Feature Learning for Networks

前面讲到 DeepWalk是一种可重复访问已访问节点的深度优先遍历算法，但是这样产生的遍历节点序列不足以捕获网络中模式的多样性。Node2Vec 定义了一种更加灵活的领域定义，并提出了一种有偏的随机游走过程。文章认为先前类似于 DeepWalk 的随机游走过程变现力不足，对网络中的一些连接模式不够敏感。

文章指出网络中的节点可以按照以下两种方式组织：

1.来自同一社区的节点。（同构性/同质性，homophily），同质性指的是距离相近节点的embedding应该尽量近；这里的同质性不是一阶、二阶这类非常局限的同质性，而是在相对较广范围内的，能够发现一个社区、一个群、一个聚集类别的“同质性”。
2.具有相似角色的节点。（结构等效性，structural equivalence），结构等效性指的是结构上相似的节点的embedding应该尽量接近；

同构性，homophily：例如对于节点 u ，s 1，s 2，s 3，s 4。都是来自同一社区的节点，因此在 Embedding 空间中的向量应该相近。
结构等效性，structural equivalence：u 和 s 6都是各自社区的中心节点，因此也应该具有相似的 Embedding。
Node2Vec 希望学习表示来最大可能地保留节点的网络领域性，也就是想捕获上面的网络连接模式。

具体如何捕获这些模式呢？其实主要工作都在随机游走上面。随机游走之后的学习过程和 DeepWalk，Word2Vec 是类似的。

具体的：需要 Embedding Function f 来最大化领域节点共现的概率。

 然后使用条件独立性：

 然后设特征空间的对称性，即 a 对 b 的作用与 b 对 a 的作用一样。然后形式化为内积和 softmax：

 进一步：

这里需要注意两点：

直接计算花费很大，本文用 Negative Sampling 方法解决的。
未必是 u 的直接邻居，只是用s方法采样得到的邻居，跟具体的采样方法有关。
到这里和 DeepWalk 没有差别，差别在于如何产生随机游走；

说到随机游走的采样，本文分析了两种图的游走方式，深度优先游走（Depth-first Sampling，DFS）和广度优先游走（Breadth-first Sampling，BFS）

 如图，假设每次随机游走采样 3 个节点（加上根节点，一共 4 个），一种 BFS 和一种 DFS 如图所示。

然后论文认为：

BFS 倾向于在初始节点的周围游走，可以反映出一个节点的邻居的微观特性；因此可以捕获结构等效性，structural equivalence。对 u 进行 BFS 可以推断该节点在网络结构中的角色。
DFS一般会跑的离初始节点越来越远，可以反映出一个节点邻居的宏观特性；因此可以基于同质性推断社区等连接模式。
既然两者都有用，那么自然结合两种模式咯。然后具体之间的权重可以根据经验对不同任务设置，也可以作为参数进行学习。

那么问题就成为了如何设计随机游走来模拟两种模式啊。

作者定义了一个概率：

 即 i-1 时刻从节点 v 下一时刻到 x 的概率。然后进一步：

 其中 是 v 和 x 之间边的权重，如果是有权图就是边的权重，无权图都设为 1。

关键来了：

上图中，对于一个随机游走，如果已经采样了 (t, v)，也就是说现在停留在节点 v 上，那么下一个要采样的节点x是哪个？

代表 t 和 x 的最短路径。也就是以如果所有边权重为 1 的情况下，谁大，就高概率采样那个节点。如果第一个概率最大，那么最有可能留在原地，如果第二个概率最大，那么最有可能采样 1 跳邻居，如果第三个概率最大，那么最有可能采样 2 跳邻居。

返回概率 p：

如果 p > max ⁡ ( q , 1 ) ，那么采样会尽量不往回走，对应上图的情况，就是下一个节点不太可能是上一个访问的节点t。
如果 p < max ⁡ ( q , 1 ) ，那么采样会更倾向于返回上一个节点，这样就会一直在起始点周围某些节点来回转来转去。
出入参数q：

如果 q > 1 ，那么游走会倾向于在起始点周围的节点之间跑，更容易反映出一个节点的 BFS 特性。
如果 q < 1 ，那么游走会倾向于往远处跑，更容易反映出 DFS 特性。
然后手动设置 p  和 q 就可以控制 DFS 和 BFS 的程度。

首先看一下算法的参数，图 G、Embedding 向量维度 d、每个节点生成的游走个数 r，游走长度 l，上下文的窗口长度 k，以及之前提到的 p、q 参数。

根据p、q和之前的公式计算一个节点到它的邻居的转移概率。
将这个转移概率加到图 G中形成 G’。
walks 用来存储随机游走，先初始化为空。
外循环 r 次表示每个节点作为初始节点要生成 r 个随机游走。
然后对图中每个节点生成一条随机游走 walk，将 walk 添加到 walks 中保存。
然后用 SGD 的方法对 walks 进行训练。

第 5 步 产生 walk 的方式：

将初始节点 u 添加进去。
walk 的长度为 l，因此还要再循环添加 l-1 个节点。
当前节点设为 walk 最后添加的节点。
找出当前节点的所有邻居节点。
根据转移概率采样选择某个邻居 s。
将该邻居添加到 walk 中。
其实本质上和 DeepWalk 都是一样的，最大的差异在于产生随机游走的时候既考虑了 DFS，也考虑了 BFS。

3.3. Line
时间上来看顺序是：DeepWalk，Line，Node2Vec，但是我这里修改顺序是因为 DeepWalk 和 Node2Vec 很相似，LINE 差异较大一些。

LINE 认为 DeepWalk 的缺点是目标函数并不是专为 Graph 设计的，而是从 NLP 语言模型中迁移过来的。

论文的主要贡献：

1.适合任意类型的网络，不论是有向图还是无向图还是带权图。并且可以扩充到很大的图
2.本文提出的目标函数同时考虑了网络局部特征和全局特征。
3.提出一种边采样的算法，可以很好地解决 SGD 的效率问题。

如下图所示，作者认为两类节点是相似的节点：

6 和 7 之间有一条前连接的边（边权重很大），图中就是更粗的线。因此是两个相似的节点。
5 和 6 即使没有直接连接，但是都和 1 2 3 4 节点相连，因此也是相似的节点。
两种相似性在文中被描述成了一阶邻近度和二阶邻近度。一阶邻近度认为两个顶点的边权重越大，两个顶点越相似。二阶邻近度认为两个顶点的共同邻居越多，两个顶点越相似。

 这里 LINE 和 Node2Vec 一样都认为 DeepWalk 是一种 DFS 的遍历，因此只能捕获二阶邻近度，也就是 Node2Vec 中的同构性。

一阶邻近度：
网络中的一阶邻近度是两个顶点之间的局部点对的邻近度。对于有边 ( u , v )连接的每对顶点，该边的权重 表示 u 和 v 之间的一阶邻近度，如果在 u 和 v 之间没有观察到边，他们的一阶邻近度为0。

二阶邻近度：
二阶相似性指的是一对顶点之间的接近程度 ( u , v ) 在网络中是其邻域网络结构之间的相似性。数学上，让表示一阶附近与所有其他的顶点，那么 u 和 v 之间的二阶相似性由 和 之间的邻近度来决定。如果没有一个顶点同时和 u 和 v 连接，那么 u 和 v 的二阶邻近度是0。

这里一阶邻近度有个问题就是：稀疏性，由于图中的边可能是缺失的，因此只捕获一阶邻近度可能会效果不太好。

具体来看一阶邻近度如何捕获的：

 其中是节点 的 embedding 之后的向量。可以看到两个向量最相近，内积越大，取符号越小，然后取倒数就越大。然后就是这个值得经验分布：

其中是节点 i 和 j 的边权重， W 是所有边权重之和，为了保留这种邻近度，期望两个分布之间的差异越小越好。因此这里的优化目标就是：

 具体来看二阶邻近度如何捕获的：

 其中 u 有上标  代表是其作为上下文节点，没有则是作为正在考虑的节点。这里和 DeepWalk 和 Node2Vec 相似，但是这里没有随机游走，而是取的 Graph 中所有的节点。然后经验分布 

其中是节点 i 的出度。优化目标就成了：

 其中代表节点的声望（也就是重要性），可以是节点的度也可以是 PageRank 值。文中设为节点的度，因此最后的优化目标就是：

最后结合两个目标：文中的方法是两个目标分别训练，然后直接连接起来，然后将联合训练留在未来工作。可以看到 Node2Vec 参考了这里一阶邻近度和二阶邻近度的概念，提出了 BFS 和 DFS 联合训练的方法。

然后就是模型优化了：

负采样：的计算非常昂贵，因为是在所有节点里面做的归一化，作者使用了经典的负采样：

这样归一化就不是在整个节点 ∣ V ∣  上面，而是在负采样数量 K 上面做的。

边采样：注意到对 的时候梯度是：

和变得权重相关，在大的复杂的实际网络中，边的权重可能有的很大有的很小。

如果设置大的学习率，面对小的边权是可以的，但是大的边权可能会梯度爆炸。
如果设置小的学习率，面对大的边权是可以的，但是小的边权可能会梯度消失，导致优化很慢。
因此作者提出了一个边采样技术：直觉想法就是在计算梯度的时候可以忽略边权，使上面问题得以解决。

第一个直观想法就是边权为 w 的边，就是 w条二元边，但是这回导致空间消耗。因为需要存放所有边权之和条边。
进一步的想法就是让采样到某条边的概率正比于边权重，这样就可以很好的解决问题。一种方法是设置区间，但是更好的方法是 alias 表采样法。这样可以导致复杂度大大下降。
讨论中有两个问题：一个是有的节点度太小了。解决方法是找它的二阶领域节点，如果两者之间权重比较大，则相加，计算两个相隔节点的权重：

第二个是新节点问题，如果是和现有的没有相连，那么需要额外信息。如果是相连的：直接优化更新

4. 总结
到这里，模型就讲的差不多了。我们简单分析一下。

1.  DeepWalk 就是 Word2Vec 在 Graph 的直接产物。
2. Node2Vec 就是同时考虑了 DFS 和 BFS 的 DeepWalk
3. LINE 其中没有随机游走，但是本质还是类似的，考虑了所谓的一阶邻近度和二阶邻近度，也就是局部和全局信息（我个人不是很认可）。

所有方法主要都是无监督的，学到的 Embedding 可以用于下游任务。

4.1 Why Graph
我们讲一个 Graph 的实际例子。

首先我们考虑一种场景，假设在电影推荐之中如果捕获电影之间的关系？我们可以把每个电影看过的人作为一个向量，然后训练。另外一种就是用 Graph。例如同一人看过的电影之间有边，并且边权可以是同时看过的人数，这样的好处：

- graph 是对复杂的连接关系建模，能够更好地学电影之间的高阶相似关系。

然后进一步：同质性可以认为是连续观看的两部电影（相邻的节点）。结构等效性就是指不同类型电影中的最火电影（角色相同）。