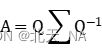机器学习原理篇：基础数学理论 Ⅰ

机器学习原理篇：基础数学理论 Ⅰ

一、前言

机器学习的理论基础就是数学基础，里面的很多模型都是建立在数学公式上的，其中数学理论主要包括微积分、线性代数、概率论、数理统计以及最优化理论等等理论知识。

我们本学期就开设了机器学习的理论课，叫代数与逻辑，如果你以后想要往这方面发展的话，是必须要理解并学习掌握这些知识的，如果只是应对期末考试或者不想往这个方向发展，那大可不必学习这么多。

感觉，我之前实践的内容更新太多了，相反理论知识总结很少，所以，打算以后也开始更新一些实践内容背后的理论知识总结，这样能更快的理解学习它们是怎么建立起来的。

二、微积分

微积分是高等数学中研究函数的微分和积分以及有关概念和应用的数学分支，它是数学的一个基础学科，内容主要包含极限、微分学、积分学及其应用。

微分学包括求导数的运算，是一套关于变化率的理论，它使得函数、速度、加速度和曲线斜率等均可用一套通用的符号进行讨论。

积分学包括求积分的运算，为定义和计算面积、体积等提供一套通用方法。

微积分的知识在人工智能算法中无处不在，求导是微积分的基本概念之一，也是很多理工科领域的基础运算。导数是变化率的极限，是用来找到“高等近似”的数学工具，是一种高等变换，体现了无穷、极限、分割的数学思想，主要用来解决极值问题。

而人工智能算法的最终目标就是要得到最优化的模型，其最后都可以转换为求极大值和极小值的问题，比如，梯度下降法和牛顿法是人工智能的基础算法，现在主流的求解代价函数最优解的方法都是基于这两种算法改造的。

级数也是微积分中非常重要的概念，常见的级数有泰勒级数、傅里叶级数等等，它们在人工智能算法中有着非常重要的地位。

其中我们简单介绍一下泰勒级数：

若函数
在包含
的某个开区间（a，b)上具有（n + 1)阶的导数，那么对于任一
有：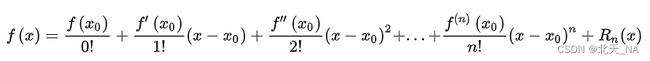

泰勒级数体现了用多项式近似和逼近函数的思想，泰勒级数在人工智能算法的底层起到了非常重要的作用，泰勒级数对理解很多基础算法的原理很有帮助。

三、线性代数

线性代数不仅仅是人工智能的基础，更是现代数学和以现代数学作为主要分析方法的众多学科基础，它研究对象是向量、向量空间、线性变换和有限的线性方程组。

线性代数中的向量和矩阵为人工智能提供了一种组合的特征描述方式，将具体事务抽象为数学对象，描述事务发展的静态和动态规律，线性代数的核心意义在于提供了一种看待世界的抽象视角，万事万物都可以被抽象成某些特征的组合，在预置规则定义的框架之下，世界以静态和动态的方式加以观察。

1、向量和矩阵

向量和矩阵不只是理论上的分析工具，也是计算机工作的基础条件。向量是人工智能中的一个关键数据结构，在计算机存储中，标量占据的是零维数组，向量占据的是n维数组，人工智能领域主要将向量理解为n维空间上的点。

矩阵是一个按照长方阵列排序的复数或实数集合，矩阵可以看作向量的组合，在计算机视觉领域，矩阵可用来表示图像，图像的基本单位是像素，一副图像是由固定行列数的像素组成的，如果每个像素都用数字表示，那么一幅图像就像是一个矩阵。

我前面在学习计算机图形学的时候总结了一篇线性代数的，可以去看看。

GAMES101-现代计算机图形学入门——Day01-线性代数基础

2、范数和内积

范数和内积是描述作为数学对象的向量时用到的特定的数学语言，范数是对单个向量大小的度量，描述的是向量自身的性质，其作用是将向量映射为一个非负的数值，常常被用来度量某个向量空间（或矩阵）中的每个向量的长度或大小。

范数计算的是单个向量的尺度，而内积计算的是两个向量之间的关系，两个相同维数的向量内积的表达式为：
即对应元素乘积后再求和。内积能够表示两个向量之间的相对位置，即表示向量之间的夹角。内积为0，在二维空间上，两个向量夹角为九十度，互相垂直，这种关系被称为正交，如果两个向量正交，则说明它们线性无关，相互独立。

在实际问题中，向量不仅表示某些数字的组合，更可能表示某些对象或某些行为的特征。范数和内积能够处理这些表示特征的数学模型，进而提取原始对象或原始行为中的隐含关系。

3、线性变换

线性空间的一个重要特征是能够承载变化。当作为参考系的标准正交基确定后，空间中的点就可以用向量表示。当这个便从一个位置移动到另一个位置时，描述它的向量自然也会改变。点的变化对应着向量的线性变换，而描述对象变换或向量线性变换的数学语言正是矩阵。

在线性空间中，变化的实现有两种方式：一是点本身的变化，二时参考系的变化。在第一种方式中，使某个点发生变化的方法是用代表变化的矩阵以代表点的向量。如果保持点不变，而换一种观察的角度，则也能得到不同的结果。在这种情况下矩阵的作用就是对正交基进行变换。因此，对矩阵和向量的乘积就存在不同的解读：Ax=y这个表达式既可以理解为向量x经过矩阵A所描述的变换编程了向量y，也可以理解为一个对象在坐标系A的度量下得到的结果为向量x，在标准坐标系I的度量下得到的结果为向量y。这表示矩阵不仅能够描述变化，也可以描述参考系本身。

4、特征值和特征向量

描述矩阵的一对重要参数是特征值和特征向量，对于给定的矩阵A，假设其特征值是λ，特征向量为x，则它们的关系是：Ax=λx。

正如前面所说，矩阵代表了向量的变换，其效果通常是对原始向量同时施加方向变化和尺度变化。可对一些特殊的向量，矩阵的作用只能改变尺度而无法改变方向，也就是只有伸缩的效果而没有旋转的效果。对于给定的矩阵来说，这类特殊的向量即矩阵的特征向量，特征向量的尺度变化系数就是特征值。

矩阵特征值和特征向量的动态意义在于表示了变化的速度和方向。如果把矩阵所代表的变化看作奔跑的人，那么矩阵的特征值就代表了这个人奔跑的速度，特征向量就代表了这个人奔跑的方向。但是，矩阵可不是普通人，它是有多个分身的人，其不同分身以不同速度（特征值）在不同方向（特征向量）上奔跑，所有分身的运动叠加在一起才是矩阵的效果。求解给定矩阵的特征值和特征向量的过程叫作特征值分解，但能够进行特征值分解的矩阵必须是 n 维方阵。将特征值分解算法推广到所有矩阵，则可以得到更加通用的矩阵分解方法一一奇异值分解。

5、奇异值分解（SVD）

奇异值分解时线性代数中的一种矩阵分解方法，是特征分解在任意矩阵上的推广。
在人工智能领域应用非常广泛，如用于特征选择、降噪、数据压缩、主成分分析（ PCA )等方面。其表达式如下：

其中 Q 是 mxm 阶酉矩阵，
是半正定 mxn 阶对角矩阵；而
，即 V 的共轭转置，
是 nxn 阶酉矩阵。这样的分解就称作 A 的奇异值分解，
对角线上的元素
，其中
即为 A 的奇异值。

矩阵经过奇异值分解后会得到一系列系数，抛弃某些较小系数，对原矩阵重建，则发现重建后误差很小。可以认为较小系数代表了原信号的粗略信息或低频信息，忽略这部分并不影响原信号的表达，而大系数代表了原信号的重要信息或高频信息。这样，就可以根据这一特性进行特征选择、主成分提取和数据压缩等操作。

四、最后我想说

下期博客继续总结接下来的概率论、数理统计以及最优化理论。