基于BiGRU和GAN的数据生成方法

本文首发于行者AI

引言

当我们期望得到与现有有限数据类似的样本时，可以考虑使用一些数据增强的方法。本文从建筑参数生成项目出发，介绍了两种数据生成方法：基于BiGRU以及GAN网络的数据生成。

BiGRU网络是由RNN发展而来，它在处理序列数据的任务中被广泛使用，1991年Elman[1]基于Jordan network[2]做了简化提出RNN，但是由于RNN中较远时间步会发生梯度消失和梯度爆炸导致RNN的应用受限，在1997年LSTM[3]网络和BiRNN[4]网络模型在RNN基础上进行改进使得RNN网络的适用范围扩大，之后Bengio团队优化了LSTM训练慢的问题提出了GRU网络。GRU网络与LSTM相差并不大，它将LSTM原有的三个门控单元减少到两个，得到了更快的收敛速度和与之不相上下的模型效果。本文使用GRU网络是因为，当面对（1：n）的样本组成的多维输入时，我们期望能够利用到所有的输入样本，刚好GRU网络满足这种训练要求。

GAN[5]是近些年比较火的研究方向，在2014年由Goodfellow提出，GAN网络的初衷就是让模型有联想能力或者说“想象力”，它可以用来生成不存在于真实世界的数据，并且生成的数据符合规则。

1. 任务描述

简述任务需求：输入一组建筑物的长和宽，希望得到满足要求的三个枚举值的组合以及随机数0~4的值，生成的枚举值和浮点数组合返回给请求端处理后，会得到新的一对长宽组合，要求计算得到的长和宽与输入的长宽差别不超过50(mm)。根据神经网络的特征，需要分开枚举值生成任务与浮点数生成任务。

提出两种实现方案：

GRU网络邻近点数据拟合： 根据任务描述可知，期望通过输入的长和宽来预测一系列数值，由于生成数据中包含了相关性不强的随机值，这给生成任务带来挑战。因此考虑利用起现有的数据，依照有监督的方法进行训练。参考与输入的长和宽邻近的n个样本数据进行拟合(邻近样本使用KD树查找)。对于枚举类型组合，统计邻近样本的枚举类型组合中每个类的数量，取数量最多的类作为输出。对于随机数组的生成，将选取的枚举类对应的随机数组组合成Data交给神经网络学习，因此交给网络的Data将是一个二维矩阵，矩阵的每一行都是一个与输入的长和宽临近样本的随机数组，为此考虑使用CNN或者RNN网络对这种多维数据提取信息，本文选用受限制的GRU网络作为数据提取方法，使用受限制的GRU在后文有详细介绍。

GAN网络数据生成： 枚举类型的生成使用GAN网络，将长和宽输入给生成器，生成器生成一组one-hot类型数据交给判别器判断。随机数组合拆分成5个分别使用MLP网络生成。

2. 数据集描述

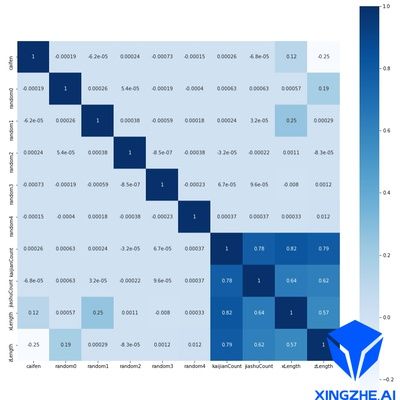
数据集有数据条目约1060万个，每个样本包含枚举类型和浮点类型的数据，枚举类型包括：材分，开间数和架数。浮点型数据包括：随机数0~4、建筑的长和宽。通过计算皮尔逊、肯德尔和斯皮尔曼相关系数(如下图)可知，随机数2~4基本上与任何特征都没有直接联系，枚举值相互之间的联系比较深刻。除此以外，在确定了建筑的长和宽后，枚举值组合也可以基本确定。 

图1.数据特征皮尔逊系数混淆矩阵

肯德尔系数

图2.数据特征肯德尔系数混淆矩阵

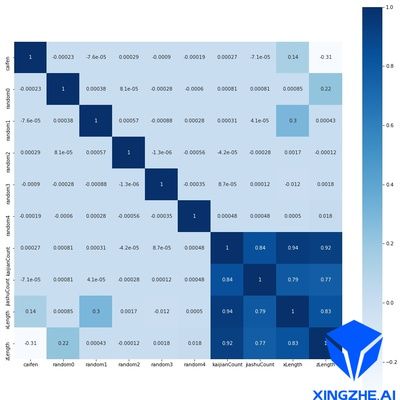
斯皮尔曼系数
图3.数据特征斯皮尔曼系数混淆矩阵

3. BiGRU生成数据

3.1 GRU数据组织方法

如何找出与输入的长和宽相邻的样本也是一个需要解决的问题，本文选择使用KD树来实现，KD树被用来实现KNN方法，它是一种平衡二叉树，KD树在构建中都会选择一个维度进行划分，每个超平面都会把该空间划分为两个部分，每次选择时都会按照中间值来划分。scipy库中有非常简便的调用方法，使用如下：

from scipy import spatial 

List_x_y = Data[:,-2:]                                              # 数据中的长宽在最后两位，取出他们
KDTree = spatial.KDTree(List_x_y)                                   # 构建KD树
position = List_x_y[i,:]                               # 组织样本时从现有的数据取

# KDTree.query会返回两个内容,索引0的部分是一组array形式的距离值,索引1是一组array形式的索引。
index = KDTree.query(position,(lib_n.search_size + 1))[1][1:]       # 这样就返回了在 List_x_y 中距离(15,20)最近的 search_size + 1 个样本点[1:]表示不取最近的那个,也就是不取它本身

现在解决了数据查询的问题，下一步需要解决样本组织形式，我们注意到确定了长和宽之后他们的枚举类型组合也基本随之确定了。一般的，对于一对长宽组合，最多有两到三个枚举类型组合，因此在样本组织过程中的搜索阶段，我们要求计算机搜索sample_size * 2个临近点(经过尝试后发现是可以找到sample_size以上个邻近样本的)，然后拿取这一组邻近样本中占比最大的sample_size个枚举类型组合的数据(带随机数组)，将这组数据拆切片只保留随机数组作为data，原本的长和宽对应的随机数组做为label，他们的枚举类型就直接认定成近邻样本中枚举值类的众数类。在实验中我们取10/20/30条数据为一个样本进行实验。以这种数据组织形式，数据的复用率很高。

3.2 Limited BiGRU网络

组成数据集后可以着手搭建网络了，使用受限制的GRU是因为我们认为所有输入样本数据都是有价值的，因此希望重置门R和更新门Z不要存在0的情况，也就是不让重置门和更新门将所有历史信息都遗忘。实现方法是压缩sigmiod这里是压缩到70%，sigmiod函数乘上压缩系数后仍有为0的情况，所以我们加上30%的历史数据作为保障，历史数据的汇入同样受更新门控制，允许至少40%的隐藏信息汇入，可以保证在每一个时间步上都有至少12%的历史信息被保留。softsign函数有比较平滑的梯度变化，样本落入饱和区间的可能性会比tanh小很多。为实现了这个受限制的GRU作为数据提取网络，主要对GRUcell部分进行了如下改进：

传统GRU单元

图4.传统GRU单元

 r = (sigma(W_{ir} x + b_{ir} + W_{hr} h + b_{hr})) * 0.7 + 0.3   # 限制sigmoid输出之后加上一个定值,可以保证这个门控信息是不会置于0的
 z = (sigma(W_{iz} x + b_{iz} + W_{hz} h + b_{hz})) * 0.6 + 0.4   # 并且仍给神经网络自适应的余地
 n = softsign(W_{in} x + b_{in} + r * (W_{hn} h + b_{hn}))        # softsign相对于tanh有着更平滑的梯度变化
 h' = (1 - z) * n + z * h 

下边给出整个网络的结构和参数

class GRU_attention(nn.Module):
    def __init__(self,lib):
        super(GRU_attention,self).__init__()
        self.gru = nn.GRU(input_size=lib.input_size,
                                  hidden_size=lib.hidden_size_01,
                                  num_layers=lib.num_layers,
                                  batch_first=lib.batch_first,
                                  bidirectional=lib.bidirectional)
                
        self.f1 = nn.Linear(lib.hidden_size_01 * 2,lib.hidden_size_02)
        self.bn1 = nn.BatchNorm1d(lib.hidden_size_02)
        self.drop1 = nn.Dropout(0.8)
        self.f2 = nn.Linear(lib.hidden_size_02,lib.output_size)
    
    def forward(self,input):
        out,_ = self.gru(input)         
  out = out[:, -1, :]
  out = F.elu(self.f1(out))
        out = self.bn1(out)
        out = self.drop1(out)
        out = self.f2(out)
        return out

class Lib_net:
    def __init__(self):
        self.input_size = 5
        self.hidden_size_01 = 128
        self.hidden_size_02 = 128
        self.output_size = 5
        self.num_layers = 4
        self.batch_first = True
        self.batch_size = 1024
        self.bidirectional = True
        self.dropout = 0.8
        self.learn_rate = 0.003
        self.directions = 2 if self.bidirectional else 1

解释一些参数，其中num_layers代表包含几层GRU单元，batch_first控制输入信息的排布，如果置为True那么输入就是(batch_size, time_step, input_size)，我也认为这样设置更符合主观判断，bidirectional代表是否使用双向网络，双向网络其实就是两个GRU结合，两个GRU的输入有所不同，一个是从第一个时间步开始向后输入，另一个是从最后一个时间步向前输入，也就是一个会积累历史信息，一个会积累未来信息，因此在一个确切的时间步的任务中，未来和历史信息会共同作用。out = out[:, -1, :] 意思是只保留最后一个时间步产出的隐藏信息。

使用到数据归一化，学习率调整，以下是代码。

# 这个是Z-score归一化，比较适用于最大最小值不确定或者未来任务中会有更改的情况
from sklearn.preprocessing import StandardScaler
Data_random = scaler_random.fit_transform(df_total[['random0','random1','random2','random3','random4']])
# 归一化参数保存
joblib.dump(scaler_random,'./Random')
# 归一化参数读取
sclar_test_random = joblib.load("./Random")
# 归一化应用
Data_random = sclar_test_random.transform(df_total[['random0','random1','random2','random3','random4']])
# 反归一化
pride_inver_random = sclar_test_random.inverse_transform(pride)

# 学习率调整 这是峰值下降法 具有自适应性 这里再推荐一个余弦退火 余弦退火在前期实验中可以帮助更好的找到更优的学习率初始值
lr = torch.optim.lr_scheduler.ReduceLROnPlateau(optimizer,'min',factor=0.8,patience=15,verbose=True,min_lr=0.00003)

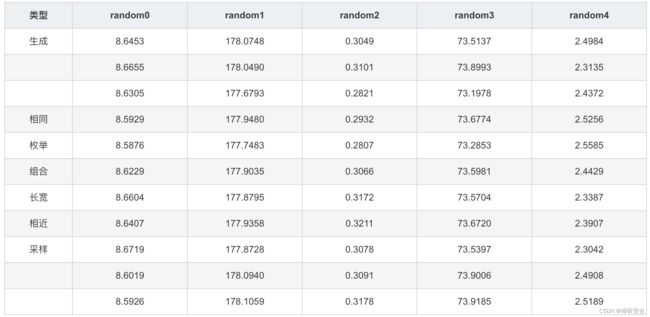
训练500轮的loss在0.72左右，最终的效果返回去不是很理想，这里给出一个生成案例：

4.GAN网络生成数据

GAN网络主要由两个网络组成，一个是判别器，一个是生成器，这两个网络的构成没有定式，还是要看确切的实验效果。GAN的思想是我们输入一组真实存在的数据，或者说是希望网络去模拟的数据，这组数据会打上True的label，也就是label = 1。然后我们将一些数据种子交给生成器，让生成器生成和真实数据相同维度的新数据。种子最好是和生成数据有逻辑上的延续但是需要保证二者不要直接影响。在生成器接收种子并生成数据之后，将这段数据作为data交给判别器，与之对应的label = 0，判别器会分别计算真实数据和生成数据的loss，loss之和即为判别器需要反向传播的loss。至于生成器的loss，就是产生的数据在判别器的判断后与label = 1计算loss。这就是GAN网络的核心思想，判别器需要尽可能判出何为真实值何为虚假值，生成器也要不断生成以假乱真的数据骗过判别器。

本文中判别器更新方法如下：

首先将data拆分成枚举值组与随机数组，枚举值组转换成onehot类型作为data交给判别器，这部分数据标签为TRUE，判别器计算后得到一组bool组合，计算第一部分loss_1。之后在符合要求的范围内随机出一组长和宽的组合交给生成器，生成器生成一组假的onehot类型数据交给判别器判断，这部分数据的标签为False，计算第二部分loss_2，与loss_1作和之后即为判别器的最终loss。

生成器更新方法如下：

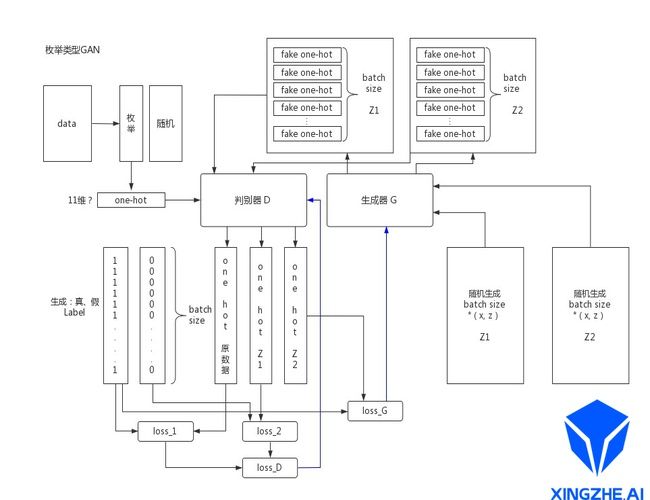
在符合要求的范围内随机出一组长和宽的组合交给生成器，生成器生成一组假的onehot类型数据交给判别器判断，这部分数据的标签为TRUE，计算得到的loss即为生成器的最终损失。流程图如下。 

图5.本文中GAN工作流

4.1 GAN实现

以下是GAN的网络结构部分：

'''
input : onehot类型的枚举数据
output: 一个值，0或1，负责判断。
'''
class Discriminator(nn.Module):
    def __init__(self, lib):
        super(Discriminator, self).__init__()
        self.fc1 = nn.Linear(lib.input_size_D, lib.hidden_size_1)
        self.fc2 = nn.Linear(lib.hidden_size_1, lib.hidden_size_2)
        self.fc3 = nn.Linear(lib.hidden_size_2, lib.hidden_size_3)
        self.fc4 = nn.Linear(lib.hidden_size_3, lib.output_size_D)
        # self.fc5 = nn.Linear(lib.hidden_size_4, lib.output_size_D)

    def forward(self, input):
        out = F.leaky_relu(self.fc1(input),0.2)
        out = F.dropout(out, 0.3)
        out = F.elu(self.fc2(out))
        out = F.dropout(out, 0.3)
        out = F.elu(self.fc3(out))
        out = F.dropout(out, 0.3)
        # out = F.leaky_relu(self.fc4(out),0.2)
        # out = F.dropout(out, 0.3)
        return torch.sigmoid(self.fc4(out))


'''
input : 随机的x,z数据
output: 假的one-hot的数据
'''
class Generator(nn.Module):
    def __init__(self, lib):
        super(Generator, self).__init__()
        self.f1 = nn.Linear(lib.input_size_G, lib.hidden_size_5)
        self.f2 = nn.Linear(lib.hidden_size_5, lib.hidden_size_6)
        self.f3 = nn.Linear(lib.hidden_size_6, lib.hidden_size_7)
        self.f4 = nn.Linear(lib.hidden_size_7, lib.output_size_G)
        # self.fc5 = nn.Linear(lib.hidden_size_8, lib.output_size_G)

    def forward(self, input):
        out = F.leaky_relu(self.f1(input),0.2)
        out = F.elu(self.f2(out))
        out = F.elu(self.f3(out))
        # out = F.leaky_relu(self.fc4(out),0.2)
        return self.f4(out)

以下为GAN的更新方法：

    for epoch in range(lib.epoch):
        for i, batch in enumerate(Loader):
            # ====+++++判别器训练+++++=====
            # 设置模型训练状态
            D_net.train()
            G_net.train()
            data,_ = batch
            # print("data:\n{}".format(data))
            data = data.to(lib.device)
            # 真实值的计算
            # 自拟label
            real_label = torch.ones(lib.batch_size, 1).type(torch.FloatTensor).to(lib.device)
            # 送入网络
            predict_real = D_net(data)
            real_score = predict_real
            # 计算 loss
            real_loss = criterion(predict_real,real_label)
            # 真实值部分计算完毕

            # 虚假值计算
            # 随机生成(x, z) 按段生成，循环取样
            if (i + 1) % 3 == 1:
                x_column = np.random.uniform(1029,1085,size = (lib.batch_size,1))
                z_column = np.random.uniform(1093,2439,size = (lib.batch_size,1))
                gen_1 = np.hstack((x_column,z_column))
            elif (i + 1) % 3 == 2:
                x_column = np.random.uniform(1381, 1456, size=(lib.batch_size, 1))
                z_column = np.random.uniform(1630, 3210, size=(lib.batch_size, 1))
                gen_1 = np.hstack((x_column, z_column))
            elif (i + 1) % 3 == 0:
                x_column = np.random.uniform(1733, 1828, size=(lib.batch_size, 1))
                z_column = np.random.uniform(2103, 3210, size=(lib.batch_size, 1))
                gen_1 = np.hstack((x_column, z_column))
            sclar_xz = joblib.load('D:/pycharm_workstation/GAN_NN_budiling/Scalers/xz')
            gen_1_re = sclar_xz.transform(gen_1)

            # 生成假标签
            fake_label = torch.zeros(lib.batch_size, 1).type(torch.FloatTensor).to(lib.device)
            gen_1_re = torch.from_numpy(gen_1_re).float().to(lib.device)
            # 生成器产出假的枚举值序列
            fake_data = G_net(gen_1_re)

            # 把生成的序列交给判别器
            predict_fake = D_net(fake_data)
            # 计算loss
            fake_loss = criterion(predict_fake,fake_label)
            # 对于判别器，总的loss等于real_loss + fake_loss
            total_loss = real_loss + fake_loss

            # 记录loss在本轮epoch均值
            loss_once_d = total_loss.item()
            Loss_epoch_D.append(loss_once_d)

            # 判别器梯度更新
            optimizer_D.zero_grad()
            total_loss.backward()
            optimizer_D.step()

            # ====+++++生成器训练+++++=====
            # 生成一组假数据
            if (i + 1) % 3 == 1:
                x_column = np.random.uniform(1029,1085,size = (lib.batch_size,1))
                z_column = np.random.uniform(1093,2439,size = (lib.batch_size,1))
                gen_2 = np.hstack((x_column,z_column))
            elif (i + 1) % 3 == 2:
                x_column = np.random.uniform(1381, 1456, size=(lib.batch_size, 1))
                z_column = np.random.uniform(1630, 3210, size=(lib.batch_size, 1))
                gen_2 = np.hstack((x_column, z_column))
            elif (i + 1) % 3 == 0:
                x_column = np.random.uniform(1733, 1828, size=(lib.batch_size, 1))
                z_column = np.random.uniform(2103, 3210, size=(lib.batch_size, 1))
                gen_2 = np.hstack((x_column, z_column))
            # 归一化
            sclar_xz = joblib.load('D:/pycharm_workstation/GAN_NN_budiling/Scalers/xz')
            gen_2_re = sclar_xz.transform(gen_2)
            # save_data_generate = gen_2
            gen_2_re = torch.from_numpy(gen_2_re).float().to(lib.device)

            # 交给生成器生成
            fake_generate = G_net(gen_2_re)

            # 交给判别器判断
            teacher = D_net(fake_generate)
            fake_score = teacher

            teacher_say = criterion(teacher,real_label)
            # 记录loss在本轮epoch均值
            loss_once_g = teacher_say.item()
            Loss_epoch_G.append(loss_once_g)

            # 生成器梯度更新
            optimizer_G.zero_grad()
            teacher_say.backward()
            optimizer_G.step()

我们想通过GAN得到枚举值的组合，因此交给判别器的data只有one-hot之后的枚举数组，然而前文中我们说过，建筑物的长和宽是枚举数组的决定性因素，在交给网络时，它虽然以复合规则范围的长和宽作为种子去生成枚举数组，但是并没有建立长和宽与枚举值的联系，也就是说判别器只知道那种枚举值组是真实存在的，并不清楚给定的长和宽对应哪几种枚举数组。因此这种数据是不合规的。

5. 解决办法

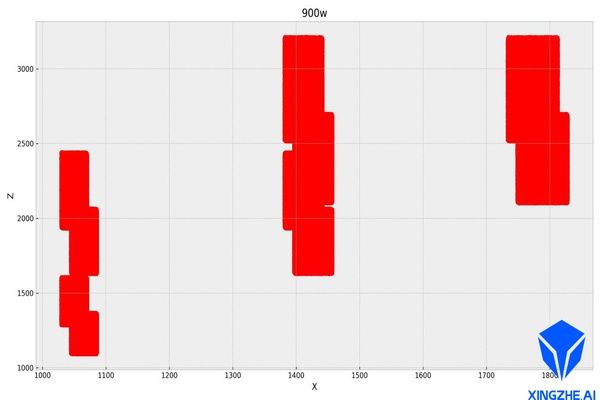
既然数据生成的办法行不通，那么就使用查询的方法，单看数据量我们有900万随机数据和160万定点生成的数据，这些数据覆盖了所有合理的长宽组合，他们的分布如下,纵轴为长，横轴为宽，单位为mm： 

图6.160万条长宽数据覆盖范围 

图7.900万条长宽数据覆盖范围

1060万的数据基本上也满足随机的需求，因此将这1060万的数据建KD树进行查询，查询返回最临近样本点，这样也避免了生成数据偏差较大的问题。

引用
[1] Elman, J. L., 1990. Finding structure in time. Cognitive science, volume 14,179–211. Doi: 10.1016/0364-0213(90)90002-E.

[2] Jordan, M. I., 1986. Serial order: A parallel distributed processing approach.Report Institute for Cognitive Science University of California. Doi:10.1016/S0166-4115(97)80111-2.

[3] Hochreiter, S., et al., 1997. Long short-term memory. Neural computation,volume 9, 1735–1780.

[4] Schuster, M., Paliwal, K. K., 1997. Bidirectional recurrent neural networks.IEEE transactions on Signal Processing, volume 45, 2673–2681. Doi:10.1109/78.650093.

[5] Goodfellow I , Pouget-Abadie J , Mirza M , et al. Generative Adversarial Nets[C]// Neural Information Processing Systems. MIT Press, 2014. https://arxiv.org/pdf/1406.2661.pdf

————————————————
版权声明：本文为CSDN博主「行者AI」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/suiyuejian/article/details/126102416