机器学习(一) 机器学习概述
文章目录
- 一、机器学习基本概念简介
-
- 1.1 机器学习的定义
- 1.2 函数的分类
- 1.3 如何寻找函数
-
- 1.3.1 定义函数
- 1.3.2 定义 Loss 函数
- 1.3.3 定义 Optimization(优化函数)
-
- 1.3.3.1 假设只有 w 需要优化时
- 1.3.3.2 将 b,w 的方向组合在一起时
- 1.4 函数的修改
-
- 1.4.1 取多天的资讯进行训练
- 二、深度学习基本概念简介
-
- 2.1sigmoid 函数定义
- 2.2sigmoid 函数如何逼近各种线段
- 2.3 建立更加弹性的函数
-
- 2.3.1 更多的 Model Features
- 2.3.2sigmoid 函数的计算方式
- 2.4 新 Loss
- 2.5 新 Optimization
- 2.6batch 与 epoch
- 2.7ReLU(Rectified Linear Unit)函数
- 2.8 多层网络及深度学习的定义
- 三、后话
一、机器学习基本概念简介
1.1机器学习的定义
我们所要求机器所能为我们做的事情均离不开两个最要的模块:输入和输出。比如对于无人驾驶来说,汽车必须根据路段信息来决定车辆的行驶,在此过程中,路段信息就是输入,车俩的行驶就是输出,但问题是他是怎么让输入变成输出的呢。而这就是机器学习所需要做的事情:寻找一个函数根据输入而输出合理的操作,表示为 f(输入)–> 输出,这也是机器学习的定义。
1.2函数的分类
在机器学习中我们知道其定义是找一个函数来根据输入做出合理的输出,在这里介绍两种常见函数:
1.Regression(回归函数):其输出是一个数值。如我们需要预测未来的PM2.5的浓度,当天的PM2.5浓度、气温、臭氧的浓度为输入然后经过一个回归函数来预测明天的PM2.5浓度。

2.Classification(分类函数):其输出为一个类别。如我们在收到邮件时,常常有些骚扰或者垃圾邮件,这些邮件便是输入,经过分类函数可以将这些归类到“垃圾邮件”类别之中

1.3如何寻找函数
1.3.1定义函数
根据之前视频播放资讯预测未来的播放量即其他比例
函数的输入是前一天的资讯,输出是今天的播放量的预测值。我们可以把函数设成一次函数:
y = b +wx1 其中b我们称为偏置参数bias,w为权重参数weight。x1是前一天的播放量,是我们所知道的,称作feature,w和b是未知的,需要我们通过学习得到的,而这样的一个带有未知参数的函数我们称作Model(模型)
1.3.2定义Loss函数
Loss函数的输入是我们在1.31所定义函数的未知参数(parameters)即:L(b, w),输出我们预测的数据更跟实际数据的差别。如:
令L=L(500, 1),则y = b + wx1 -> y = 500 + x1 假设有下面时间的播放量:

对于2017/1/2这一天,当b=500,w=1时,x1等于2017/1/1的播放量根据所设函数计算y=500+4800 = 5300,即我们预测01/02号这天的播放量是5300,但从开始的资讯中我们可知实际这天的实际播放量是4900,则en=abs(5300 - 4900)。同样的方法,我们都可以算出每一天的误差。则最终的Loss = 1/N ∑en,N表示有N份学习资料。我们也可以推出在不同b和w值下Loss是不一样的,而机器要做的就是寻找一组最合适的b,w值从而使Loss最小,提高预测的精确度
1.3.3定义Optimization(优化函数)
在 1.3.2 中我们知道要寻找一组最合适的 b,w 值的过程就是不断优化未知函数的过程,而最常用的方法就是梯度下降法(Gradient Descent)
1.3.3.1假设只有w需要优化时
w* = arg minLoss,假设Loss函数与w关系如下:

首先随机找一个w的初始值w0,计算在w0的L对w的微分∂L/∂w(w=w0)也就是斜率:
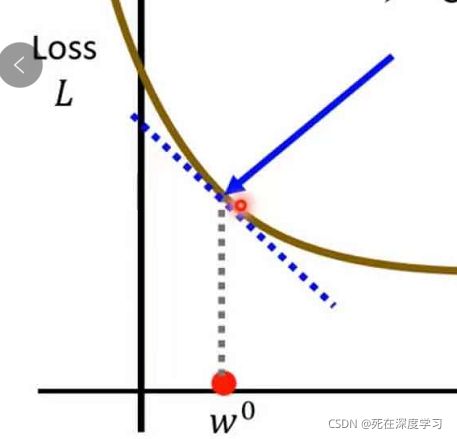
从图中我们可以观察到此偏导是负的,所以在w0左边的虚线比较高,右边比较低,这样的话我们可以提高w的值来使Loss值减小(偏导如果是正的则相反),有:

在图中又有了一个新的参数为η,我们称作学习率(Learing rate),η值越大,w值更新越快,越小则w值更新越慢。而η是需要我们在实验过程中手动设置的参数,我们将这一类参数叫做超参数(hyperparameters),由图我们也能得出w与Loss的微分关系:w1-w0=η*∂L/∂w(w=w0),以此方法训练数据得到Loss的最小值,此时gradient为0
同样,b的值也是以这种方法不断更新
1.3.3.2将b,w的方向组合在一起时
w*,b* = arg minLoss,可视化后:
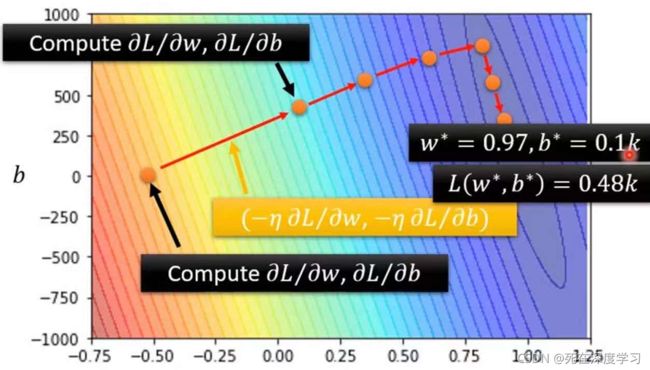
当w* = 0.97(接近1),b* = 100(一般设的比较小)Loss值达到最小480,因此我们拿出这组数据来预测一下;
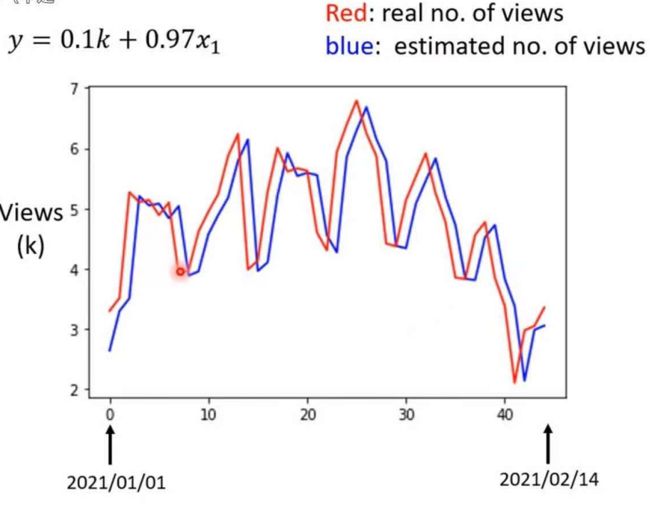
可以看出大致的方向是能够拟合的,但是预测的播放量的低估总是比实际的出现晚一两天,这可能出现的原因是我们在预测是只用前一天的数据就行预测,数据量太少,因此我们就要修改我们的Model。
1.4函数的修改
1.4.1取多天的资讯进行训练
考虑7天时,函数由y = b + wx1 变成y = b + ∑wjxj(j从1到7)每一天的播放量都乘上对应的w值,Loss值变化及对应的b,w值如下:

L表示训练数据上的损失,L‘表示预测未知数据的损失。随着参考天数的增加,Loss值实在减小,而表格中w有正由负,负表示前一天的播放量与我们预测的那天的播放量是成反比的,从函数的表达式我们也能得到这个结论,w为正则相反。
当我们继续考虑28天和56天时:
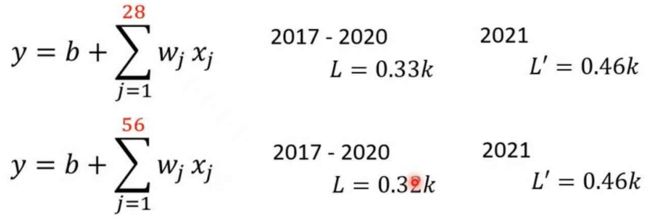
我们发现考虑天数对Loss值的影响已经变化不大,因此这应该是极限了。
而以上我们所设和修改后的函数模型称作线性模型(Linear Models)
二、深度学习基本概念简介
前言:Linear Models对我们解决应用场景问题来说太过于简单了,因为Linear Medols永远都只是一条直线,你可以通过修改w值来改变斜率和修改b来修改斜距,但是其永远是直线。
而我们需要的可能是一段斜率是正的,而一段是负的,此时线性模型就永远不能满足这一点,显然Linear Models有着许多的限制,而这种来自于Models的限制叫做Model Bias,注意不是我们上面所设函数中的b参数。因此,我们需要更加有弹性的函数来实现图中红色线段。
2.1sigmoid函数定义
上述的红色曲线可以由一个常数项加上一堆s型折线的和来实现
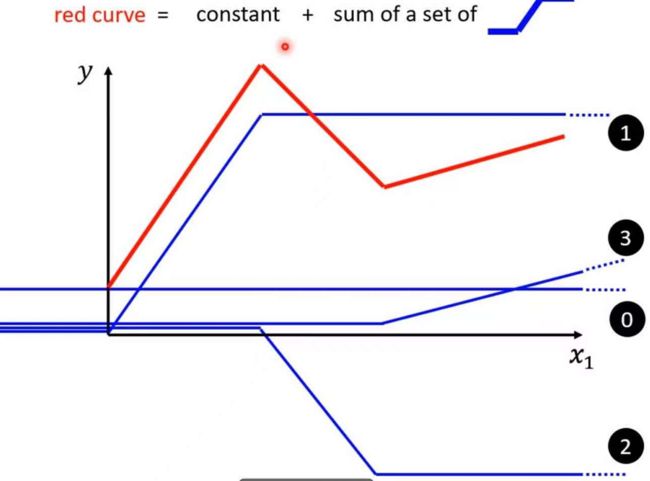
从0,1,2,3蓝色曲线分别取与红色曲线相对应的部分即可构成红色曲线。依照这种方法,无论所求的曲线有多复杂,折点有多多,我们都可以用一个常数项加不同数的s性折线构成。而要写出s性折线的函数表达式并不是很容易,所以我们可以用一条光滑的曲线去逼近它,这个曲线函数就是sigmoi函数:
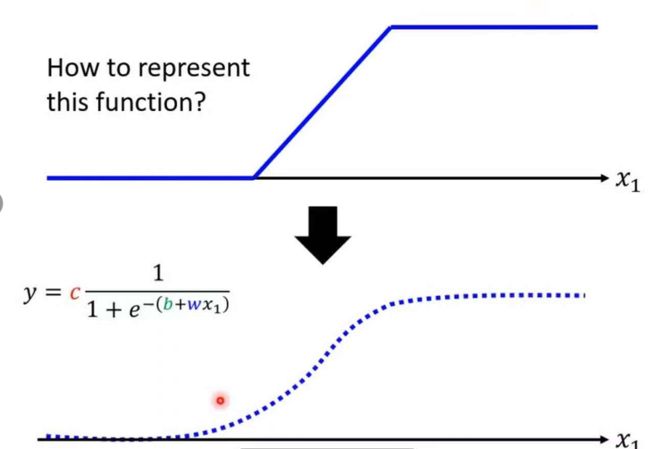
从sigmoid函数表达式中y = c*[1 / (1 + e-(b + wx1))](注意表达式中的b是Models bias)看出当x1非常大是函数值会收敛到c的位置,当x1非常小时,函数值会收敛到0。sigmoid函数可写成y = c * sigmoid(b + wx1)
2.2sigmoid函数如何逼近各种线段
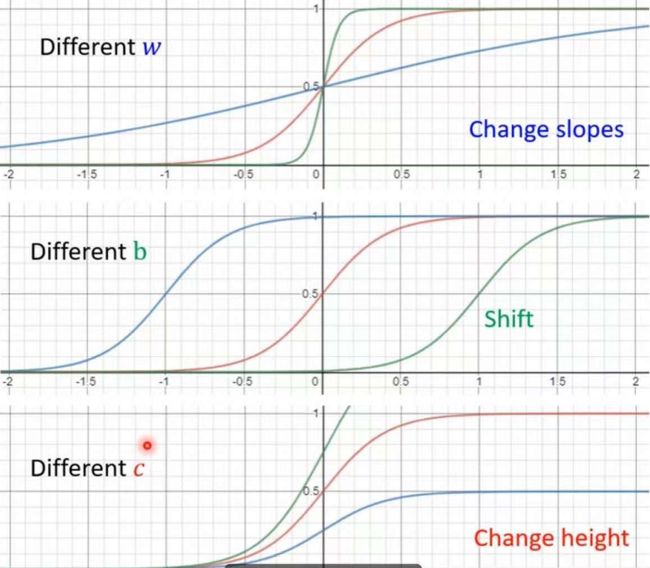
1.改变w值可以改变sigmoid函数图像的斜率
2.改变b的值可以让sigmoid函数图像左右移动
3.修改c的值可以改变sigmoid函数图像的高度
2.3建立更加弹性的函数
2.3.1更多的Model Features
当我们用很多的sigmoid函数去形成一条复杂的函数图像时,每一个sigmoid函数中参数c,b,w都是不一样的。
当我们只用一天的数据去预测未来的播放量时,函数可变成
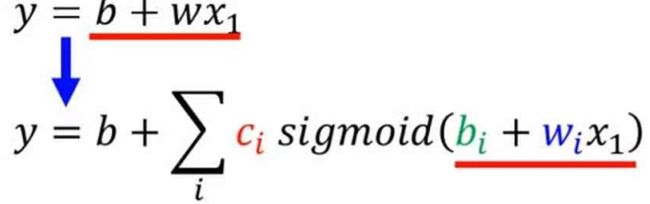
其中i表示sigmoid函数的个数
当用多天数据时,函数可变成
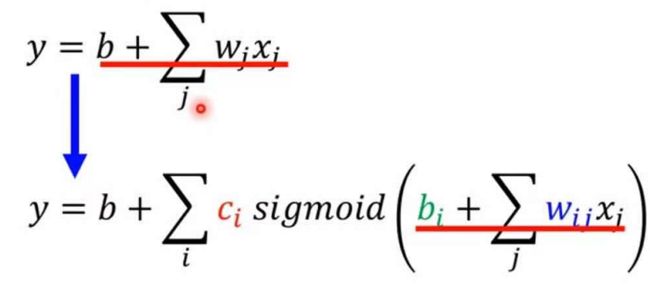
其中i代表sigmoid函数个数,j代表天数,xj表示第前j天的播放量
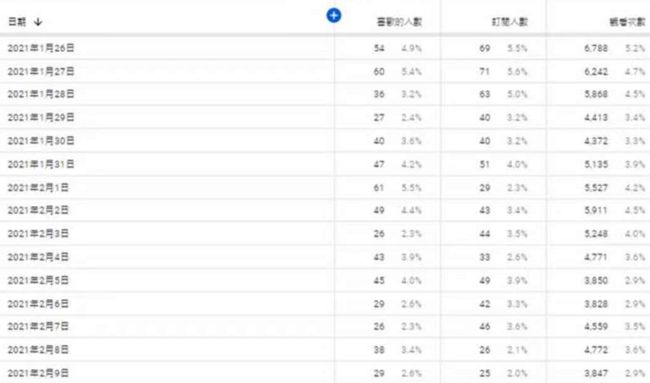
2.3.2sigmoid函数的计算方式
其中x1,x2,x3表示该天的播放量,wij表示乘给xj的播放量的weight。把b1+w11x1+w12x2+w13x3相加送到第一个sigmoid函数中计算,第二、三个sigmoid函数也是这样计算。为了简化计算过程,我们可以用矩阵的方法来计算,令
r1=b1+w11x1+w12x2+w13x3
r2=b2+w21x1+w22x2+w23x3
r3=b3+w31x1+w32x2+w33x3

再令a=sigmoid(r)=1 / (1 + e-r),再乘每个sigmoid函数的c再相加有!
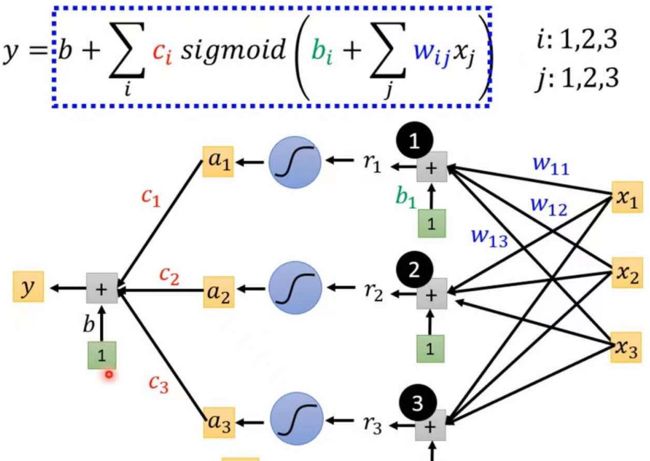
如果将三个sigmoid函数的过程整合成矩阵计算的话,如下:
r = b + wx
a = sigmoid(r)
y = b + cT(c 矩阵的转置)a
即 y = b + cT sigmoid(b + wx)
2.4新Loss
在 y = b + cT sigmoid(b + wx)中,我们将所有矩阵的每一列或者每一行整合在一起得到一个大的矩阵 θ
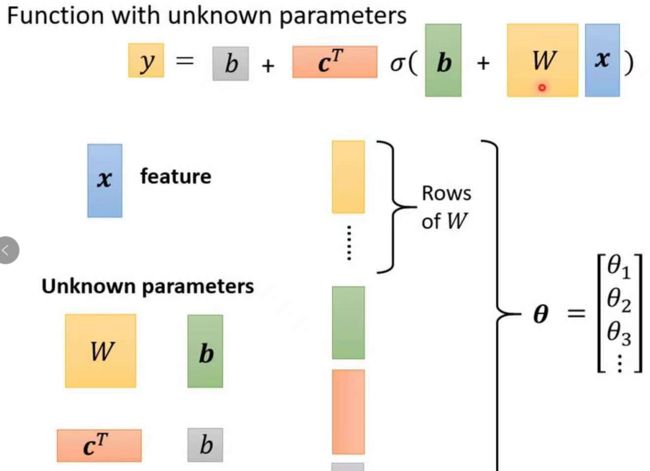
所以Loss函数每一组的参数可以用 L(θ)来表示,计算方法跟只有w,b时是一样的,只不过现在可能是几百,几千个参数
2.5新Optimization
计算方法参数的更新方法跟只有w,b时是一样的
θ* = arg minLoss θ = [θ1 θ2 θ3…]T
2.6batch与epoch
当我们有一笔N资料时,要去计算Loss时,我们可以将N笔资料分成M份,每一份有N/M笔资料,N/M笔资料就叫做一个batch,而我们可以先计算每一个batch的Loss’,然后更新参数 θ,计算出gradient。当所有batch都看过一遍之后叫做epoch
2.7ReLU(Rectified Linear Unit)函数
ReLU是现在深度学习最常用的激活函数,表达式为
y = b + ∑ci max(0, ∑wijxj)
可以看出ReLU是分段函数,当∑wijxj > 0时,y = ∑wijxj,当∑wijxj <= 0时,y = 0 图像为

且可以看出两个ReLU函数才能组成一个sigmoid函数
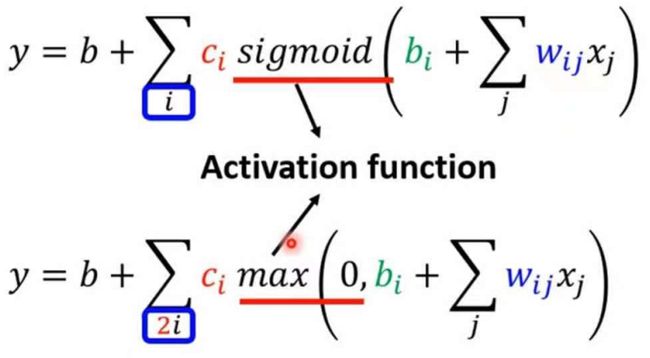
它们都是激活函数,一般来说ReLU的拟合效果比sigmoid函数好,因此ReLU更加常用
2.8多层网络及深度学习的定义
之前所有的讨论都是只经过一次激活函数,但是我们可以通过多层的激活函数进行预测结果,一层激活函数的输出可以作为下一层的输入,所以层与层之间的参数是不相同的

注意两个 a 向量是不同的
在预测我们一开始的视频播放量时,当经过一百层的ReLU函数后,Loss与预测和实际播放量的拟合程度如下图:
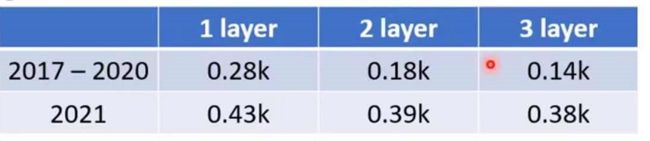
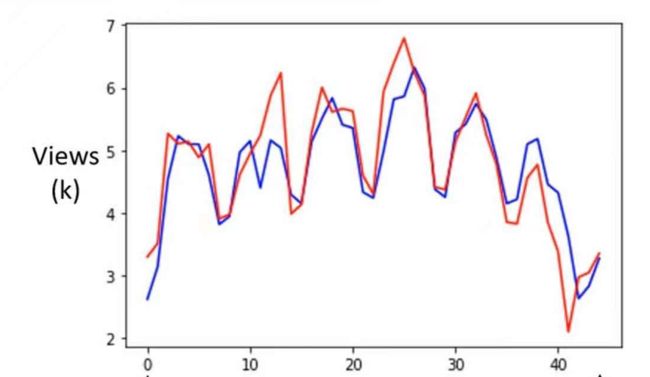
在上面的许多层的ReLU或者sigmoid,被称作Neuron(神经元),很多的Neuron就叫做Neural Network,许多许多的隐藏层就叫做Deep,而这一套分析计算技术就叫做Deep Learning
三、后话
此系列文章是我学习深度学习的一些笔记,可能过程中有些错误,欢迎大家指正,不胜感激!与君共勉