IMU_tk阅读

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

---

前言

因为工作需要，有个标定任务，根据需要选用了IMU_tk 作为本任务的标定工具，为了深入研究标定思想和原理，决定深入阅读imu_tk 代码（MATLAB版本）

---

一、imu_tk用途？

imu_tk 是一款imu传感器的标定工具包，主要目的是为了标定陀螺仪和加速度计的内参（刻度因子、安装误差、零偏）。

二、源码阅读

imu_tk 工具包可以上github下载

2.1加速度计的标定

imu_tk工具 首先标定加速度计 其次标定陀螺仪

2.1.1加速度计的标定原理

传感器的选型需要对其特性进行测试，需要测试的特性有：零偏温度滞回特性，震动特性，重复上电对于bias的影响，应力对于对bias的影响，基于优化的配准方法，非线性因子；
（本着尊重原创的原则给出原文链接：https://mp.weixin.qq.com/s/-0n1KagBzsXOpHv1GNHWoQ）

• 零偏温度滞回特性：指传感器在温度上升阶段和温度下降阶段对应的bias不一致，有个差值，如果差值比较小则校准精度会比较好，反之校准误差就比较大，影响融合结果（如下图），图片来自上文的链接

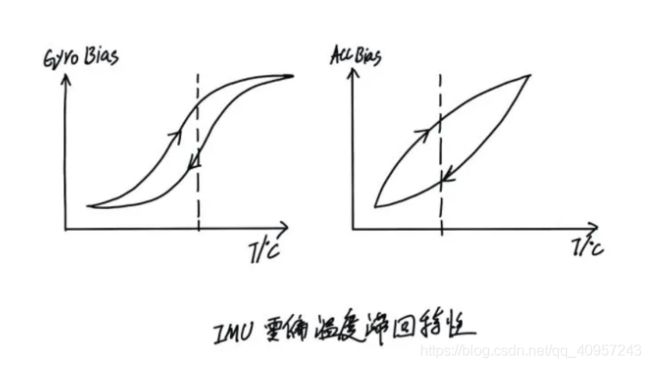
加速度计的标定常用的6面法，12面法，但是校准思想均是一致的，本文主要记录imu_tk中的方法

加速度计的校准主要是以重力加速度为基准的，在静止情况下三轴的模理论值应该等于重力加速度，加速度计标定9个参数，下面给出具体方程：

A为acc真值，M为安装对准误差，S为刻度因子，a为acc的测量值，B为acc的bias；

2.1.2加速度计的标定源码阅读

下载解压后打开calibrate.m文件，本文件为标定程序的入口文件；

标定离不开原始数据的输入：

IMU0x2Dalpha.mat   %加速度计数据
IMU0x2Domega.mat  %陀螺仪数据

% 扣除偏移量后的原始数据
a_xp = IMU0x2Dalpha(:,2)' - offset_acc_x*ones(1,total_sample);
a_yp = IMU0x2Dalpha(:,3)' - offset_acc_y*ones(1,total_sample);
a_zp = IMU0x2Dalpha(:,4)' - offset_acc_z*ones(1,total_sample);
omega_x = IMU0x2Domega(:,2)' - offset_gyro_x*ones(1,total_sample);
omega_y = IMU0x2Domega(:,3)' - offset_gyro_y*ones(1,total_sample);
omega_z = IMU0x2Domega(:,4)' - offset_gyro_z*ones(1,total_sample);

标定时数据的静态探测尤为重要，var_3D 为加速度计静态时的3个方向平方和，以此为基准进行静态探测，w_d为景天探测时的滑动窗口

var_3D = (var(a_xp(1:3000))^2 + var(a_yp(1:3000))^2 + var(a_zp(1:3000))^2);
w_d = 101;               % 

以101为窗口滑动计算三个方向的均方根差，s_square为滑动计算的方差和

for i = (half_w_d + 1):total_sample - (half_w_d + 1)
   normal_x(i) = var(a_xp(i - half_w_d:i + half_w_d));
   normal_y(i) = var(a_yp(i - half_w_d:i + half_w_d));
   normal_z(i) = var(a_zp(i - half_w_d:i + half_w_d));
end

s_square = (normal_x.^2 + normal_y.^2 + normal_z.^2);

滑动探测s_square和阈值进行对比探测状态，阈值分别1var_3D、2var_3D … 10*var_3D；

挑选静态数据段>100的数据段，根据步长重新组成加速度计不同位置的静态数据；

例：探测的静态数据段为220，步长（step=floor（220/fre））为2，fre为频率（本例程中为100Hz），根据步长挑选100个数据作为本位置的静态数据

循环往复，最终得到各个位置的静态数据段，构建残差函数（默认重力加速度为：9.81744；需要注意的是不同地理位置重力加速度不相同）；最终采用lsqnonlin（）函数进行最小二乘解算；（不同的阈值选取的数据段不同，根据不同的阈值，计算出lsq残差最小原则选取标定好的参数）
注：函数lsqnonlin()使用方法见：https://blog.csdn.net/qq_40957243/article/details/115166655

2.2、陀螺仪的标定

陀螺仪的标定是基于加速度计的标定，imu_tk 首先标定的是加速度计，其次标定陀螺仪。

2.2.1陀螺仪的标定原理

本次标定陀螺仪的参数主要是安装对准误差，刻度因子，零偏，其中零偏采用初始静止状态的均值计算，关于安装对准误差和刻度因子的方程如下：

其中G为陀螺仪真值，M为安装对准误差，S为刻度因子，U为扣除零偏的测量数据。

陀螺仪标定的思想：利用陀螺仪计算得到的姿态和真实姿态之间有一定的差异，该差异主要由于陀螺仪内参引起，根据该差异便可以计算内参，但是真实姿态未知，因此需要利用重力矢量与计算姿态在重力方向投影之间的残差，根据该残差便可以计算内参；（阅读代码的个人理解：确定3段数据，首尾为静态数据，中间为动态旋转数据，根据首尾两段标定好的加速度计数据的均值便可以得到旋转前后的姿态，根据中间旋转的陀螺仪数据积分便可以得到旋转矩阵，根据初始的姿态+旋转矩阵便可以推算末尾的姿态，利用第三段已知的姿态和推算的姿态便可以得到残差，依次类推计算标定参数）

2.2.2陀螺仪的标定源码阅读

标定陀螺仪时仅仅标定刻度因子 和 安装对准误差，零偏可采用初始时刻静态数据的均值计算，代码如下，可以看到是将原始数据扣除零偏后再进行标定

estimate_bias_x = mean(omega_x(init_long_qs_interval_start:init_long_qs_interval_end));
estimate_bias_y = mean(omega_y(init_long_qs_interval_start:init_long_qs_interval_end));
estimate_bias_z = mean(omega_z(init_long_qs_interval_start:init_long_qs_interval_end));

omega_x = omega_x - estimate_bias_x;
omega_y = omega_y - estimate_bias_y;
omega_z = omega_z - estimate_bias_z;

从原始数据中挑选出静态数据位置，

QS_time_interval_info_matrix(1:3, l) = [start; i - 1; samples];

start：为静态数据段的起始位置，i-1：为数据段结束位置，samples：为静态数据段的长度；

挑选出加速度计标定后的静态数据，每段数据挑100组数据，求均值；

selected_acc_data(1:3, i)  % 挑选出标定后的加速度数据 

QS_time_interval_info_matrix(4:6, l) = mean(selected_acc_data, 2);%求取静止时间段的加速度均值

构建陀螺仪残差函数：

gyroCostFunctLSQNONLIN(theta_pr_gyro, QS_time_interval_calib_info_matrix, omega_x, omega_y, omega_z)

同理，利用lsqnonlin()函数进行陀螺仪9参数的解算 。

总结

本文主要记录的作者在阅读imu_tk 工具时的学习历程，记录了加计和陀螺仪的标定思想以及代码中需要注意的点。