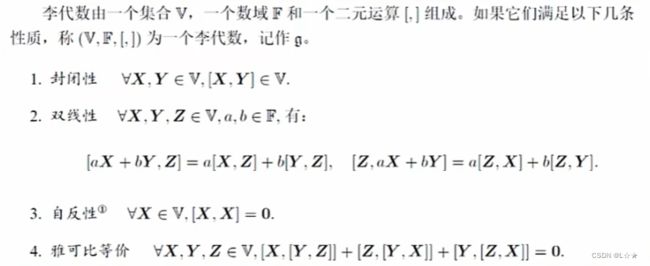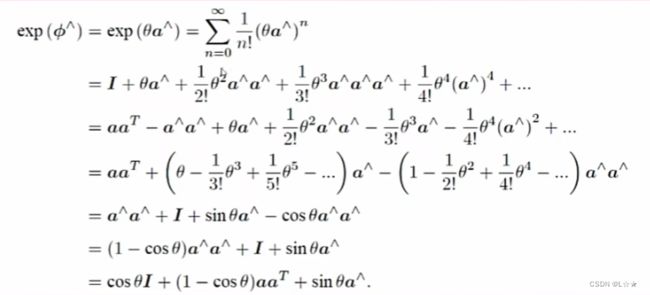视觉SLAM十四讲ch4笔记——李群与李代数
文章目录
- 视觉SLAM十四讲ch4——李群与李代数
-
- 4.1 李群李代数基础
- 4.2 指数映射和对数映射
-
- 4.2.1 s o ( 3 ) ↔ S O ( 3 ) so(3) \leftrightarrow SO(3) so(3)↔SO(3)
- 4.2.2 s e ( 3 ) ↔ S E ( 3 ) se(3) \leftrightarrow SE(3) se(3)↔SE(3)
- 4.2.3 小总结: s o ( 3 ) ↔ S O ( 3 ) so(3) \leftrightarrow SO(3) so(3)↔SO(3)、 s e ( 3 ) ↔ S E ( 3 ) se(3) \leftrightarrow SE(3) se(3)↔SE(3)的转换关系
- 4.3 李代数求导与扰动模型
-
- 4.3.1 引入李代数的原因
- 4.3.2 李代数求导方法
- 4.3.3 小结
- 4.4 演示:SOPHUS库
视觉SLAM十四讲ch4——李群与李代数
4.1 李群李代数基础
什么是群?
群(Group)是一种集合加上一种运算的代数结构- 记集合为 A A A, 运算为 ⋅ \cdot ⋅,那么运算满足以下性质时,称 ( A , ⋅ ) (A, \cdot) (A,⋅)成群。
封结幺逆的运算 (凤姐咬你)
举例:
当 A A A为整数时,运算为 + + +, A , ⋅ A, \cdot A,⋅成群
-
可以验证:
- 旋转矩阵集合和矩阵乘法 构成群
- 同样变换矩阵和矩阵乘法也构成群
- 因此,称它们为旋转矩阵群 和 变换矩阵群
-
其他常见群
- 一般线性群 G L ( n ) GL(n) GL(n):指 n × n n \times n n×n的可逆矩阵,它们对矩阵乘法成群
- 特殊正交群 S O ( n ) SO(n) SO(n):也就是所谓的旋转矩阵群,其中 S O ( 2 ) SO(2) SO(2)和 S O ( 3 ) SO(3) SO(3)最为常见
- 特殊欧式群 S E ( n ) SE(n) SE(n):也就是前面提到的 n n n维欧式变换,如 S E ( 2 ) SE(2) SE(2)和 S E ( 3 ) SE(3) SE(3)。
-
群结构保证了在群上的运算具有良好的性质。
-
群论是研究群的各种结构和性质的理论,具体见各种抽象代数或近世代数教材 -
李群(Lie Group)- 具有
连续(光滑)性质的群 - 既是群,也是流形。
- 直观上看,一个刚体能够连续地在空间中运动,故 S O ( 3 ) SO(3) SO(3) 和 S E ( 3 ) SE(3) SE(3)都是李群
- 但是, S O ( 3 ) SO(3) SO(3) 和 S E ( 3 ) SE(3) SE(3)只有定义良好的乘法,没有加法,所以难以进行取极限、求导等操作。但是在位姿估计领域需要对其求导取极限,以寻找最优解,因此这也就是位姿估计的主要研究难点之一。
- 具有
-
李代数:与李群对应的一种结构,位于向量空间- 通常记作小写的 s o ( 3 ) so(3) so(3) 或 s e ( 3 ) se(3) se(3)
- 事实上是李群单位元处的正切空间。
-
李代数的引出:
-
任意旋转矩阵 R \boldsymbol{R} R,满足
R R T = I \boldsymbol{RR}^{\text{T}} = \boldsymbol{I} RRT=I -
考虑 R \boldsymbol{R} R 随时间的变化,有:
R ( t ) R ( t ) T = I (1) \boldsymbol{R}(t)\boldsymbol{R}(t)^{\text{T}} = \boldsymbol{I} \tag{1} R(t)R(t)T=I(1)
- 两侧对时间求导:
R ( t ) ˙ R ( t ) T + R ( t ) R ( t ) T ˙ = 0 (2) \dot{\boldsymbol{R}(t)}\boldsymbol{R}(t)^{\text{T}} + \boldsymbol{R}(t)\dot{\boldsymbol{R}(t)^{\text{T}}} = 0 \tag{2} R(t)˙R(t)T+R(t)R(t)T˙=0(2)
- 整理得:
R ( t ) ˙ R ( t ) T = − ( R ( t ) ˙ R ( t ) T ) T (3) \dot{\boldsymbol{R}(t)}\boldsymbol{R}(t)^{\text{T}} = -\left ( \dot{\boldsymbol{R}(t)}\boldsymbol{R}(t)^{\text{T}}\right)^{\text{T}} \tag{3} R(t)˙R(t)T=−(R(t)˙R(t)T)T(3)
- 可以看出来,上式为一个反对称矩阵,注意 ϕ ( t ) \phi(t) ϕ(t)为一个向量,记:
R ( t ) ˙ R ( t ) T = ϕ ( t ) ∧ (4) \dot{\boldsymbol{R}(t)}\boldsymbol{R}(t)^{\text{T}} = \phi(t)^{\wedge} \tag{4} R(t)˙R(t)T=ϕ(t)∧(4)
- 这里需要注意
反对称符号的引入:即一个向量 a a a的上尖为一个反对称矩阵 A A A, 反对称矩阵 A A A的下尖为向量 a a a
a ∧ = A = [ 0 − a 3 a 2 a 3 0 − a 1 − a 2 a 1 0 ] , A ∨ = a a^{\wedge}=\boldsymbol{A}=\begin{bmatrix} 0 & -a_3 & a_2\\ a_3 & 0 & -a_1\\ -a_2 & a_1 & 0 \end{bmatrix}, \space \space \boldsymbol{A}^{\vee } = a a∧=A=⎣⎡0a3−a2−a30a1a2−a10⎦⎤, A∨=a
-
两侧同时右乘 R ( t ) \boldsymbol{R}(t) R(t),得
R ( t ) ˙ = ϕ ∧ R ( t ) (5) \dot{\boldsymbol{R}(t)} = \phi^{\wedge} \boldsymbol{R}(t) \tag{5} R(t)˙=ϕ∧R(t)(5) -
可以看到,对 R \boldsymbol{R} R 求导后,左侧多出一个 ϕ ( t ) ∧ \phi(t)^{\wedge} ϕ(t)∧
-
考虑简单的情况: t 0 = 0 , R ( 0 ) = I t_0 = 0, \boldsymbol{R}(0) = \boldsymbol{I} t0=0,R(0)=I,即上式微分方程从 0 0 0时刻开始,对 t 0 t_0 t0开始,进行一阶泰勒展开,得到:
R ( t ) ≈ R ( t 0 ) + R ( t 0 ) ˙ ( t − t 0 ) = I + ϕ ( t 0 ) ∧ ( t ) (6) \begin{aligned} \boldsymbol{R}(t) &\approx \boldsymbol{R}(t_0) + \dot{\boldsymbol{R}(t_0)}(t-t_0) \\ &= \boldsymbol{I} + \phi(t_0)^{\wedge}(t) \end{aligned} \tag{6} R(t)≈R(t0)+R(t0)˙(t−t0)=I+ϕ(t0)∧(t)(6) -
可见 ϕ \phi ϕ 反映了一阶导数性质,它位于单位圆附近的
正切空间(tangent space)上。-
在 t 0 t_0 t0附近,假设 ϕ \phi ϕ 不变,则根据公式(5),有微分方程:
R ( t ) ˙ = ϕ ( t 0 ) ∧ R ( t ) = ϕ 0 ∧ R ( t ) (7) \dot{\boldsymbol{R}(t)} = \phi(t_0)^{\wedge}\boldsymbol{R}(t)=\phi_0^{\wedge} \boldsymbol{R}(t) \tag{7} R(t)˙=ϕ(t0)∧R(t)=ϕ0∧R(t)(7) -
已知初始情况: R ( 0 ) = I \boldsymbol{R}(0) = \boldsymbol{I} R(0)=I,解之,得:
R ( t ) = exp ( ϕ 0 ∧ t ) (8) \boldsymbol{R}(t) = \exp(\phi_0^{\wedge}t) \tag{8} R(t)=exp(ϕ0∧t)(8) -
公式(8)说明,对任意 t t t,都可以找到一个 R \boldsymbol{R} R和一个 ϕ \phi ϕ的对应关系:
- 该关系为指数映射(Exponential Map)
- 这里的 ϕ \phi ϕ称为 S O ( 3 ) SO(3) SO(3) 对应的李代数: s o ( 3 ) so(3) so(3)
-
-
问题:
- s o ( 3 ) so(3) so(3) 的定义和性质?
- 指数映射如何求?
-
-
李代数(Lie Algebra)-
每个李群都有与之对应的李代数。
-
李代数描述了李群单位源数的正切空间性质
-
李代数需要满足的性质:
封自双雅(疯子爽鸭)
-
-
其中二元运算 [ , ] [,] [,]被称为李括号(Lie Bracket)
- 直观上说,李括号表达了两个元素的差异
-
例子:三维空间向量 + 叉积运算 构成 李代数
-
李代数 s o ( 3 ) so(3) so(3):
s o ( 3 ) = { ϕ ∈ R 3 , Φ = ϕ ∧ ∈ R 3 × 3 } (9) so(3) = \left \{ \phi \in \mathbb{R}^3, \Phi=\phi^{\wedge}\in \mathbb{R}^{3 \times 3} \right \} \tag{9} so(3)={ϕ∈R3,Φ=ϕ∧∈R3×3}(9)-
其中:
Φ = ϕ ∧ = [ 0 − ϕ 3 ϕ 2 ϕ 3 0 − ϕ 1 − ϕ 2 ϕ 1 0 ] ∈ R 3 × 3 \Phi = \phi ^{\wedge } = \begin{bmatrix} 0 & -\phi_3 & \phi_2 \\ \phi_3 & 0 & -\phi_1\\ -\phi_2 & \phi_1 & 0 \end{bmatrix} \in \mathbb{R}^{3 \times 3} Φ=ϕ∧=⎣⎡0ϕ3−ϕ2−ϕ30ϕ1ϕ2−ϕ10⎦⎤∈R3×3 -
李括号:
[ ϕ 1 , ϕ 2 ] = ( Φ 1 Φ 2 − Φ 2 Φ 1 ) ∨ [\phi_1, \phi_2] = (\Phi_1 \Phi_2 - \Phi_2\Phi_1)^{\vee} [ϕ1,ϕ2]=(Φ1Φ2−Φ2Φ1)∨
-
-
同理,对于李代数 s e ( 3 ) se(3) se(3):
s e ( 3 ) = { ξ = [ ρ ϕ ] ∈ R 6 , ρ ∈ R 3 , ϕ ∈ s o ( 3 ) , ξ ∧ = [ ϕ ∧ ρ 0 T 0 ] } (10) se(3) = \left \{ \xi = \begin{bmatrix} \rho \\ \phi \end{bmatrix} \in \mathbb{R}^6, \rho \in \mathbb{R}^3, \phi \in so(3), \xi^{\wedge} = \begin{bmatrix} \phi^{\wedge} & \rho \\ \boldsymbol{0}^{\text{T} } & 0 \end{bmatrix} \right\} \tag{10} se(3)={ξ=[ρϕ]∈R6,ρ∈R3,ϕ∈so(3),ξ∧=[ϕ∧0Tρ0]}(10)- s e ( 3 ) se(3) se(3) 由三个平移分量 和 三个旋转分量 组成
- 旋转和 s o ( 3 ) so(3) so(3) 相同
- 平移是普通的向量——注意,不是 S E ( 3 ) SE(3) SE(3)上的平移分量!!
- 上尖尖 ∧ ^{\wedge} ∧ 不再是反对称矩阵,但仍保留记法:
ξ ∧ = [ ϕ ∧ ρ 0 T 0 ] ∈ 4 × 4 \xi^{\wedge} =\begin{bmatrix} \phi^{\wedge} & \rho \\ \boldsymbol{0}^{\text{T} } & 0 \end{bmatrix} \in \mathbb{4 \times 4} ξ∧=[ϕ∧0Tρ0]∈4×4
- 李括号
[ ξ 1 , ξ 2 ] = ( ξ 1 ∧ ξ 2 ∧ − ξ 2 ∧ ξ 1 ∧ ) ∨ [\xi_1, \xi_2] = (\xi_1^{\wedge}\xi_2^{\wedge}- \xi_2^{\wedge}\xi_1^{\wedge})^{\vee} [ξ1,ξ2]=(ξ1∧ξ2∧−ξ2∧ξ1∧)∨
- 这里需要注意的是:
- 不同书籍对 s e ( 3 ) se(3) se(3) 的平移/旋转分量的先后顺序定义不同。这里使用平移在前的方式,也有些地方是旋转在前。
- 把李代数理解成向量形式或者矩阵形式都可以的。向量形式更自然一些。
4.2 指数映射和对数映射
4.2.1 s o ( 3 ) ↔ S O ( 3 ) so(3) \leftrightarrow SO(3) so(3)↔SO(3)
- s e ( 3 ) se(3) se(3) 由三个平移分量 和 三个旋转分量 组成
-
指数映射反映了李代数到李群的对应关系:
R = exp ( ϕ ∧ ) (11) \boldsymbol{R} = \exp(\phi^{\wedge}) \tag{11} R=exp(ϕ∧)(11)- 但是 ϕ ∧ \phi^{\wedge} ϕ∧ 是一个矩阵,对于矩阵,如何定义求指数运算呢?——Taylor展开
exp ( ϕ ∧ ) = ∑ n = 0 ∞ 1 n ! ( ϕ ∧ ) n (12) \exp(\phi^{\wedge }) = \sum_{n=0}^{\infty}\frac{1}{n!}(\phi ^{\wedge})^n \tag{12} exp(ϕ∧)=n=0∑∞n!1(ϕ∧)n(12)
-
由于 ϕ \phi ϕ 是向量,定义其角度和模长:
- 角度乘单位向量: ϕ = θ a \phi = \theta a ϕ=θa
- 关于 a a a,可以验证以下性质:
a ∧ a ∧ = a a T − I (13 a) a^{\wedge}a^{\wedge} = aa^{\text{T}}-\boldsymbol{I} \tag{13 a} a∧a∧=aaT−I(13 a)
a ∧ a ∧ a ∧ = − a ∧ (13 b) a^{\wedge}a^{\wedge}a^{\wedge} = -a^{\wedge} \tag{13 b} a∧a∧a∧=−a∧(13 b)
- 这为化解Taylor展开式中的高阶项提供了有效的方法
-
Taylor 展开:
- 最后得到一个似曾相识的结果:
exp ( θ a ∧ ) = cos θ I + ( 1 − cos θ ) a a T + sin θ a ∧ (14) \exp(\theta a^{\wedge}) = \cos \theta \boldsymbol{I} + (1-\cos\theta)aa^{\text{T}} + \sin \theta a^{\wedge} \tag{14} exp(θa∧)=cosθI+(1−cosθ)aaT+sinθa∧(14)
- 公式(14)即为:
罗德里格斯公式,罗德里格斯公式能够将旋转向量转换为旋转矩阵,这说明李代数到李群的转化为罗德里格斯公式 - 这说明 s o ( 3 ) so(3) so(3) 的物理意义就是旋转向量
- 反之,给定旋转矩阵时,亦能求李代数(对数运算):
ϕ = ln ( R ) ∨ = ( ∑ n = 0 ∞ ( − 1 ) n n + 1 ( R − I ) n + 1 ) ∨ (15) \phi = \ln (\boldsymbol{R})^{\vee}=\left ( \sum_{n=0}^{\infty } \frac{(-1)^n}{n+1}(\boldsymbol{R} - \boldsymbol{I})^{n + 1} \right)^{\vee} \tag{15} ϕ=ln(R)∨=(n=0∑∞n+1(−1)n(R−I)n+1)∨(15)
-
但是实际应用当中,没必要这样求,在旋转向量小节中已经介绍过矩阵到向量的转换关系:
θ = arccos ( tr ( R ) − 1 2 ) (16 a) \theta = \arccos(\frac{\text{tr}(\boldsymbol{R}) - 1}{2}) \tag{16 a} θ=arccos(2tr(R)−1)(16 a)R n = n (16 b) \boldsymbol{R}n = n \tag{16 b} Rn=n(16 b)
-
至此,说明了 S O ( 3 ) SO(3) SO(3) 和 s o ( 3 ) so(3) so(3) 的对应关系。
- s o ( 3 ) → S O ( 3 ) so(3) \to SO(3) so(3)→SO(3) :指数运算,也就是罗德里格斯公式
- S o ( 3 ) → s O ( 3 ) So(3) \to sO(3) So(3)→sO(3):对数运算
4.2.2 s e ( 3 ) ↔ S E ( 3 ) se(3) \leftrightarrow SE(3) se(3)↔SE(3)
-
指数映射:
exp ( ξ ∧ ) = [ ∑ n = 0 ∞ 1 n ! ( ϕ ∧ ) n ∑ n = 0 ∞ 1 ( n + 1 ) ! ( ϕ ∧ ) n ρ 0 T 1 ] ≜ [ R J ρ o T 1 ] = T (17) \begin{aligned} \exp (\xi ^{\wedge}) &= \begin{bmatrix} \sum_{n=0}^{\infty}\frac{1}{n!}(\phi^{\wedge})^n & \sum_{n=0}^{\infty}\frac{1}{(n + 1)!}(\phi^{\wedge})^n\rho \\ \boldsymbol{0}^\text{T} & 1 \end{bmatrix} \\ &\triangleq \begin{bmatrix} \boldsymbol{R} & \boldsymbol{J}_\rho \\ \boldsymbol{o}^\text{T} & 1 \end{bmatrix} \\ &= \boldsymbol{T} \end{aligned} \tag{17} exp(ξ∧)=[∑n=0∞n!1(ϕ∧)n0T∑n=0∞(n+1)!1(ϕ∧)nρ1]≜[RoTJρ1]=T(17)- 左上角表示李代数的平移部分到矩阵平移部分,相差一个线性变换(雅可比矩阵),由 J \boldsymbol{J} J给出:
J = sin θ θ I + ( 1 − sin θ θ ) a a T + 1 − cos θ θ a ∧ (18) \boldsymbol{J} = \frac{\sin \theta }{\theta }\boldsymbol{I} + \left ( 1 - \frac{\sin \theta }{\theta } \right )aa^{\text{T}} + \frac{1 - \cos \theta }{\theta } a^{\wedge } \tag{18} J=θsinθI+(1−θsinθ)aaT+θ1−cosθa∧(18)
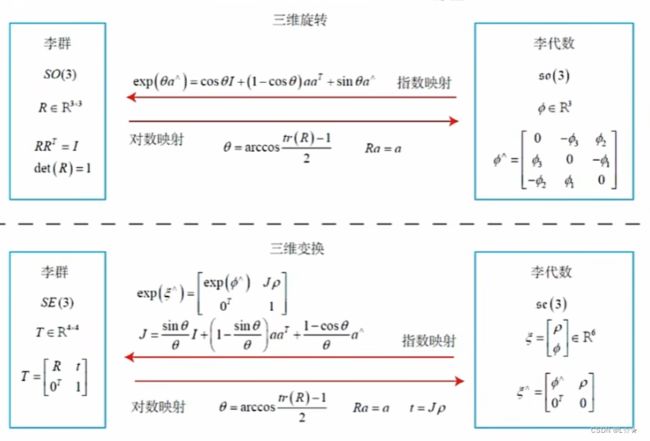
4.2.3 小总结: s o ( 3 ) ↔ S O ( 3 ) so(3) \leftrightarrow SO(3) so(3)↔SO(3)、 s e ( 3 ) ↔ S E ( 3 ) se(3) \leftrightarrow SE(3) se(3)↔SE(3)的转换关系
4.3 李代数求导与扰动模型
4.3.1 引入李代数的原因
- 在实际应用当中,我们经常需要对位姿进行估计
- 但李群元素只有乘法,没有加法,无从定义导数:
R 1 + R 2 ∉ S O ( 3 ) \boldsymbol{R}_1 + \boldsymbol{R}_2 \notin SO(3) R1+R2∈/SO(3)
4.3.2 李代数求导方法
-
那么如何对李群进行求导呢?
-
直观的想法:
- 能否利用李代数上的加法,定义李群元素的导数?
- 能否使用指数映射和对数映射完成变换关系
-
基本问题:当在李代数中做加法时,是否等价于在李群上做乘法?
exp ( ϕ 1 ∧ ) exp ( ϕ 2 ∧ ) ? = exp ( ( ϕ 1 + ϕ 2 ) ∧ ) (19) \exp(\phi_1^{\wedge}) \exp(\phi_2^{\wedge}) ?= \exp((\phi_1 + \phi_2)^{\wedge}) \tag{19} exp(ϕ1∧)exp(ϕ2∧)?=exp((ϕ1+ϕ2)∧)(19)-
在使用标量的情况下,显然,公式(19)是成立的
-
但这里的 ϕ ∧ \phi^{\wedge} ϕ∧ 为矩阵!显然公式(19)不成立的
-
完整形式的
BCH(Backer-Campbell-Hausdorff)公式给出:-
完整形式非常复杂,需要自行百度
-
部分展开式:(方括号为李括号)
ln ( exp ( A ) exp ( B ) ) = A + B + 1 2 [ A , B ] + 1 12 [ A , [ A , B ] ] − 1 12 [ B , [ A , B ] ] + ⋯ (20) \ln(\exp(\boldsymbol{A}) \exp(\boldsymbol{B})) =\boldsymbol{A} + \boldsymbol{B} + \frac{1}{2}[\boldsymbol{A}, \boldsymbol{B}] + \frac{1}{12}[\boldsymbol{A}, [\boldsymbol{A}, \boldsymbol{B}]] - \frac{1}{12}[\boldsymbol{B}, [\boldsymbol{A}, \boldsymbol{B}]] + \cdots \tag{20} ln(exp(A)exp(B))=A+B+21[A,B]+121[A,[A,B]]−121[B,[A,B]]+⋯(20) -
特别的是,当 A \boldsymbol{A} A或者 B \boldsymbol{B} B特别小时,可以只保留一阶项
-
即:当 A \boldsymbol{A} A或者 B \boldsymbol{B} B 其中一个量为小量时,忽略其高阶项,
BCH具有线性近似形式:
ln ( exp ( ϕ 1 ∧ ) exp ( ϕ 2 ∧ ) ) ∨ ≈ { J l ( ϕ 2 ) − 1 ϕ 1 + ϕ 2 if ϕ 1 is small, J r ( ϕ 1 ) − 1 ϕ 2 + ϕ 1 if ϕ 2 is small. (21) \ln(\exp(\phi_1^{\wedge }) \exp(\phi_2^{\wedge}))^{\vee} \approx \begin{cases} \boldsymbol{J}_l(\phi_2)^{-1}\phi_1 + \phi_2 & \text{ if } \phi_1 \text{ is small,} \\ \boldsymbol{J}_r(\phi_1)^{-1}\phi_2 + \phi_1 & \text{ if } \phi_2 \text{ is small.} \end{cases} \tag{21} ln(exp(ϕ1∧)exp(ϕ2∧))∨≈{Jl(ϕ2)−1ϕ1+ϕ2Jr(ϕ1)−1ϕ2+ϕ1 if ϕ1 is small, if ϕ2 is small.(21) -
其中:
- 左乘雅可比矩阵:
J l = J = sin θ θ I + ( 1 − sin θ θ ) a a T + 1 − cos θ θ a ∧ \boldsymbol{J}_l = \boldsymbol{J} = \frac{\sin \theta}{\theta }\boldsymbol{I} + \left ( 1 - \frac{\sin \theta }{\theta } \right ) aa^{\text{T}} + \frac{1 - \cos \theta}{\theta}a^{\wedge } Jl=J=θsinθI+(1−θsinθ)aaT+θ1−cosθa∧
J l − 1 = θ 2 cot θ 2 I + ( 1 − θ 2 cot θ 2 ) a a T − θ 2 a ∧ \boldsymbol{J}_l^{-1} = \frac{\theta }{2}\cot \frac{\theta }{2}\boldsymbol{I} + \left (1 - \frac{\theta }{2} \cot\frac{\theta }{2} \right )aa^{\text{T}} - \frac{\theta}{2}a^{\wedge } Jl−1=2θcot2θI+(1−2θcot2θ)aaT−2θa∧
- 右乘雅可比矩阵:
J r ( ϕ ) = J l ( − ϕ ) \boldsymbol{J}_r(\phi ) =\boldsymbol{J}_l(-\phi ) Jr(ϕ)=Jl(−ϕ)
-
后续以左乘为例展开
-
以左乘为例,直观的写法:
-
在李群行左乘小量时,李代数上的加法相差左雅克比矩阵的逆
exp ( Δ ϕ ∧ ) exp ( ϕ ∧ ) = exp ( ( ϕ + J l − 1 ( ϕ ) Δ ϕ ) ∧ ) (22) \exp(\Delta \phi^{\wedge }) \exp (\phi ^{\wedge }) = \exp\left ( ( \phi + \boldsymbol{J}_l^{-1}(\phi) \Delta\phi )^{\wedge } \right ) \tag{22} exp(Δϕ∧)exp(ϕ∧)=exp((ϕ+Jl−1(ϕ)Δϕ)∧)(22) -
反之:
exp ( ( ϕ + Δ ϕ ∧ ) ∧ ) = exp ( ( J l Δ ϕ ) ∧ ) exp ( ϕ ∧ ) = exp ( ϕ ∧ ) exp ( ( J r Δ ϕ ) ∧ ) (23) \exp\left ( (\phi + \Delta \phi^{\wedge })^{\wedge } \right ) = \exp \left ((\boldsymbol{J}_l \Delta \phi)^{\wedge } \right ) \exp (\phi ^{\wedge }) = \exp (\phi ^{\wedge }) \exp\left ( ( \boldsymbol{J}_r\Delta\phi )^{\wedge } \right ) \tag{23} exp((ϕ+Δϕ∧)∧)=exp((JlΔϕ)∧)exp(ϕ∧)=exp(ϕ∧)exp((JrΔϕ)∧)(23)- 李代数上进行小量加法时,相当于李群上左(右)乘一个带左(右)雅可比的量
-
s e ( 3 ) se(3) se(3) 上形式更复杂:
exp ( Δ ξ ∧ ) exp ( ξ ∧ ) ≈ exp ( ( J l − 1 Δ ξ + ξ ) ∧ ) (24 a) \exp (\Delta \xi ^{\wedge }) \exp (\xi ^{\wedge }) \approx \exp \left((\mathcal{J}_l^{-1} \Delta\xi + \xi)^{\wedge} \right ) \tag{24 a} exp(Δξ∧)exp(ξ∧)≈exp((Jl−1Δξ+ξ)∧)(24 a)exp ( ξ ∧ ) exp ( Δ ξ ∧ ) ≈ exp ( ( J r − 1 Δ ξ + ξ ) ∧ ) (24 b) \exp (\xi ^{\wedge }) \exp (\Delta \xi ^{\wedge }) \approx \exp \left((\mathcal{J}_r^{-1} \Delta\xi + \xi)^{\wedge} \right ) \tag{24 b} exp(ξ∧)exp(Δξ∧)≈exp((Jr−1Δξ+ξ)∧)(24 b)
-
-
-
通过
BCH线性近似,可以定义李代数上的导数 -
考虑一个基本问题:旋转后的点 p p p关于旋转的导数:
不严谨地记为: ∂ R p ∂ R \text{不严谨地记为: }\frac{\partial \boldsymbol{R}p}{\partial \boldsymbol{R}} 不严谨地记为: ∂R∂Rp -
由于 R \boldsymbol{R} R 没有加法,导数无从定义
-
存在两种解决方法:
- 对 R \boldsymbol{R} R 对应的李代数加上小量,求相对于小量的变化率(导数模型)
- 对 R \boldsymbol{R} R 左乘或者右乘一个小量,求相对于小量的李代数的变化率(扰动模型)
-
导数模型
- 按照定义可以推出:
∂ ( exp ( ϕ ∧ ) p ) ∂ ϕ = lim δ ϕ → 0 exp ( ( ϕ + δ ϕ ) ∧ ) p − exp ( ϕ ∧ ) p δ ϕ = lim δ ϕ → 0 exp ( ( J l δ ϕ ) ∧ ) exp ( ϕ ∧ ) p − exp ( ϕ ∧ ) p δ ϕ ≈ lim δ ϕ → 0 ( I + ( J l δ ϕ ) ∧ ) exp ( ϕ ∧ ) p − exp ( ϕ ∧ ) p δ ϕ = lim δ ϕ → 0 ( J l δ ϕ ) ∧ exp ( ϕ ∧ ) p δ ϕ = lim δ ϕ → 0 − ( exp ( ϕ ∧ ) p ) ∧ J l δ ϕ δ ϕ = − ( R p ) ∧ J l (25) \begin{aligned} \frac{\partial (\exp (\phi^\wedge) p)}{\partial \phi} &= \lim_{\delta \phi \to 0} \frac{\exp \left ((\phi + \delta \phi )^\wedge \right )p - \exp(\phi ^\wedge )p}{\delta \phi } \\ &= \lim_{\delta \phi \to 0} \frac{\exp \left ((\boldsymbol{J}_l \delta \phi )^\wedge \right) \exp (\phi ^\wedge )p - \exp(\phi ^\wedge )p}{\delta \phi }\\ &\approx \lim_{\delta \phi \to 0} \frac{\left ( \boldsymbol{I} + (\boldsymbol{J}_l \delta \phi )^\wedge \right ) \exp (\phi ^\wedge )p - \exp(\phi ^\wedge )p}{\delta \phi } \\ &= \lim_{\delta \phi \to 0} \frac{(\boldsymbol{J}_l \delta \phi )^\wedge \exp(\phi ^\wedge )p}{\delta \phi } \\ &= \lim_{\delta \phi \to 0} \frac{- (\exp(\phi ^\wedge )p)^\wedge \boldsymbol{J}_l \delta \phi }{\delta \phi } \\ &= -(\boldsymbol{R}p)^\wedge \boldsymbol{J}_l \end{aligned} \tag{25} ∂ϕ∂(exp(ϕ∧)p)=δϕ→0limδϕexp((ϕ+δϕ)∧)p−exp(ϕ∧)p=δϕ→0limδϕexp((Jlδϕ)∧)exp(ϕ∧)p−exp(ϕ∧)p≈δϕ→0limδϕ(I+(Jlδϕ)∧)exp(ϕ∧)p−exp(ϕ∧)p=δϕ→0limδϕ(Jlδϕ)∧exp(ϕ∧)p=δϕ→0limδϕ−(exp(ϕ∧)p)∧Jlδϕ=−(Rp)∧Jl(25)
- 结果中含有左乘雅可比矩阵,比较复杂,因此可以尝试消除
-
扰动模型
- 左乘小量,令其李代数为零:( S O ( 3 ) SO(3) SO(3) 上的扰动模型)
∂ ( R p ) ∂ φ = lim φ → 0 exp ( φ ∧ ) exp ( ϕ ∧ ) p − exp ( ϕ ∧ ) p φ ≈ lim φ → 0 ( 1 + φ ∧ ) exp ( ϕ ∧ ) p − exp ( ϕ ∧ ) p φ = lim φ → 0 φ ∧ R p φ = lim φ → 0 − ( R p ) ∧ φ φ = − ( R p ) ∧ (26) \begin{aligned} \frac{\partial(\boldsymbol{R}p)}{\partial \varphi} &= \lim_{\varphi \to 0} \frac{\exp(\varphi^\wedge) \exp (\phi ^\wedge)p - \exp (\phi ^\wedge)p}{\varphi} \\ &\approx \lim_{\varphi \to 0} \frac{(1 + \varphi^\wedge) \exp (\phi ^\wedge )p - \exp (\phi ^\wedge )p}{\varphi } \\ &= \lim_{\varphi \to 0} \frac{\varphi^\wedge \boldsymbol{R}p}{ \varphi} \\ &= \lim_{\varphi \to 0} \frac{-(\boldsymbol{R}p) ^\wedge \varphi}{ \varphi} \\ &= -(\boldsymbol{R}p) ^\wedge \end{aligned} \tag{26} ∂φ∂(Rp)=φ→0limφexp(φ∧)exp(ϕ∧)p−exp(ϕ∧)p≈φ→0limφ(1+φ∧)exp(ϕ∧)p−exp(ϕ∧)p=φ→0limφφ∧Rp=φ→0limφ−(Rp)∧φ=−(Rp)∧(26)
- 可以看出,相对于导数模型,扰动模型的最终结果更简洁,也更为实用
-
S E ( 3 ) SE(3) SE(3) 上的扰动模型:
∂ T p ∂ δ ξ = lim δ ξ → 0 exp ( δ ξ ∧ ) exp ( ξ ∧ ) p − exp ( ξ ∧ ) p δ ξ ≈ lim δ ξ → 0 ( I + δ ξ ∧ ) exp ( ξ ∧ ) p − exp ( ξ ∧ ) p δ ξ = lim δ ξ → 0 δ ξ ∧ exp ( ξ ∧ ) p δ ξ = lim δ ξ → 0 [ δ ϕ ∧ δ ρ 0 T 0 ] [ R p + t 1 ] δ ξ = lim δ ξ → 0 [ δ ϕ ∧ ( R p + t ) + δ ρ 0 ] δ ξ = [ I − ( R p + t ) ∧ 0 T 0 T ] ≜ ( T p ) ⊙ (27) \begin{aligned} \frac{\partial \boldsymbol{T}p}{\partial \delta \boldsymbol{\xi}} &= \lim_{\delta \boldsymbol{\xi} \to 0} \frac{\exp (\delta \boldsymbol{\xi}^\wedge )\exp (\boldsymbol{\xi}^\wedge )p - \exp (\boldsymbol{\xi }^\wedge )p}{\delta \boldsymbol{\xi }} \\ &\approx \lim_{\delta \boldsymbol{\xi} \to 0} \frac{(\boldsymbol{I} + \delta \boldsymbol{\xi}^\wedge) \exp (\boldsymbol{\xi}^\wedge )p - \exp (\boldsymbol{\xi }^\wedge )p}{\delta \boldsymbol{\xi }} \\ &= \lim_{\delta \boldsymbol{\xi} \to 0} \frac{\delta \boldsymbol{\xi}^\wedge \exp (\boldsymbol{\xi}^\wedge )p}{\delta \boldsymbol{\xi }} \\ &= \lim_{\delta \boldsymbol{\xi} \to 0} \frac{\begin{bmatrix} \delta \phi ^\wedge & \delta \rho \\ 0^\text{T} & 0 \end{bmatrix} \begin{bmatrix} \boldsymbol{R}p+t \\ 1 \end{bmatrix}}{\delta \boldsymbol{\xi }} \\ &= \lim_{\delta \boldsymbol{\xi} \to 0} \frac{\begin{bmatrix} \delta \phi ^\wedge(\boldsymbol{R}p+t) + \delta \rho \\ 0 \end{bmatrix}}{\delta \boldsymbol{\xi }} \\ &= \begin{bmatrix} \boldsymbol{I} & -(\boldsymbol{R}p+t)^\wedge \\ \boldsymbol{0}^\text{T} & \boldsymbol{0}^\text{T} \end{bmatrix} \\ &\triangleq (\boldsymbol{T}p)^{\odot } \end{aligned} \tag{27} ∂δξ∂Tp=δξ→0limδξexp(δξ∧)exp(ξ∧)p−exp(ξ∧)p≈δξ→0limδξ(I+δξ∧)exp(ξ∧)p−exp(ξ∧)p=δξ→0limδξδξ∧exp(ξ∧)p=δξ→0limδξ[δϕ∧0Tδρ0][Rp+t1]=δξ→0limδξ[δϕ∧(Rp+t)+δρ0]=[I0T−(Rp+t)∧0T]≜(Tp)⊙(27)
-
4.3.3 小结
- 利用
BCH线性近似,可以推导 s o ( 3 ) so(3) so(3) 和 s e ( 3 ) se(3) se(3) 上的导数模型和扰动模型 - 通常情况下,扰动模型形式更为简单,所以更常用一些
4.4 演示:SOPHUS库
GitHub链接:https://github.com/gaoxiang12/slambook
本节对应的是 ch4