阿里天池工业蒸汽量预测baseline-数据探索篇

赛题介绍

本题是很经典的特征预测题，网上有很多大佬的baseline，但是我觉得还是看官方出的赛题书好一些，这一节，总结了该题中如何去分析原始数据的思路与常用方法

赛题数据与代码在文末我的github链接里,需要的朋友可以去pull下看，喜欢的话，给个star哈

赛题数据

赛题提供了训练集和测试集，训练集提供了38个特征变量和一个target(预测目标)变量，测试集只提供了38个特征变量，我们的目标就是使用训练集训练出来的模型，结合测试集中的特征变量去预测target字段

# 数据探索
import numpy as np
import pandas as pd 
import matplotlib.pyplot as plt 
import seaborn as sns 
from scipy import stats
import warnings
warnings.filterwarnings("ignore")
%matplotlib inline

# 载入训练集与数据集
train_data_file = "./zhengqi_train.txt"
test_data_file = "./zhengqi_test.txt"

# 读取数据
train_data = pd.read_csv(train_data_file,sep='\t',encoding='utf-8')
test_data = pd.read_csv(test_data_file,sep='\t',encoding='utf-8')

# 查看集合的所有特征数据大撒东方大厦
train_data.head(10)
test_data.head(10)

训练集

测试集

评估指标

在预测模型中常用的是评价标准是均方误差MSE,在sklearn库中可以直接调库计算MSE

from sklearn.metrics import mean_squared_error
mean_squared_error(y_test,y_predict)

异常检测

箱形图

数据分析

实现预测模型之前，我们对于原始数据还要进行初步分析，由于数据集中有38个特征，这些特征中有些不一定都能用上，所以我们要分析其中的相关性，由于数据集是多变量，可以采用以下方法分析

• 绘制散点图，观察变量之间是线性还是非线性
• 计算相关性，相关性公式如下

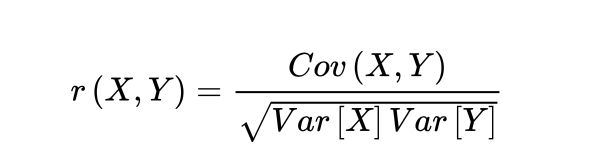
相关系数的取值范围为[-1,1],为-1时，表示强负线性相关，为1时表示正线性相关，为0，表示不相关

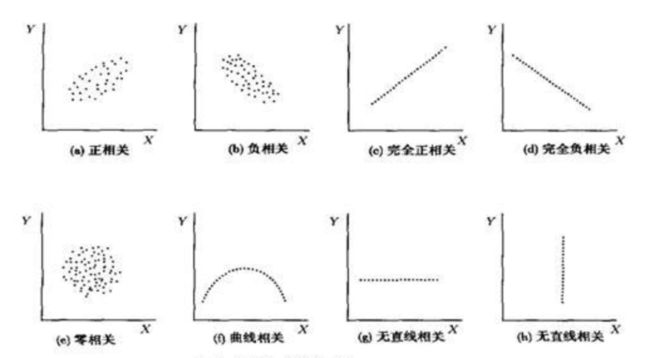
使用numpy库中的corrcoef函数可以对两种变量进行相关性检测

而原始数据往往存在异常值，缺失值这些噪声，需要我们手动对数据集进行修正，对于缺失值，可以有三种方法

• 直接删除数据，这样很简单，但是会使样本减少，拟合能力降低
• 均值，模型，中值填充
• 预测模型填充

远远偏离样本总体观测值的数据称为异常值，对于异常值检测，常用的工具是箱线图，直方图，散点图等，对于异常值的处理方法一般采用删除，转换，填充，区别对待等方式

下面通过实际的代码来演示对训练集数据进行检测的过程

首先绘制一下V0特征的箱形图

fig = plt.figure(figsize=(4,6)) # 绘制图形
sns.boxplot(train_data['V0'],orient="v",width=0.5)

可以看到很多数据位于4分位点以下，说明有异常值，接下来绘制下所有特征的箱形图

# 绘制每一列的箱线图
column = train_data.columns.tolist()[:39]
fig = plt.figure(figsize=(80,60),dpi=75)
for i in range(38):
    plt.subplot(7,8,i+1)
    sns.boxplot(train_data[column[i]],orient="v",width=0.5)
    plt.ylabel(column[i],fontsize=36)
plt.show()

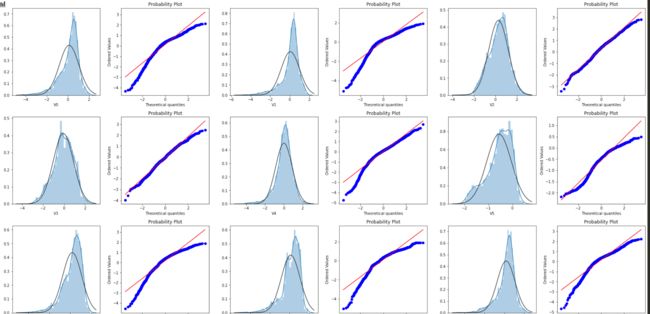
同时可以使用直方图和QQ图对数据进行分析，QQ图是指数据的分位数和正态分布的氛分位数对比参照的图，如果数据符合正态分布，所有数据都会分布在直线上,现在对V0特征进行分析

# 直方图的绘制
plt.figure(figsize=(10,5))
ax = plt.subplot(1,2,1)
sns.distplot(train_data['V0'],fit=stats.norm)
ax = plt.subplot(1,2,2)
res = stats.probplot(train_data['V0'],plot=plt)

很明显，V0特征并不符合正态分布，接下来看看其他特征的分布情况

# 绘制所有正太分布图
train_cols = 6
train_rows = len(train_data.columns)
plt.figure(figsize=(4 * train_cols,4 * train_rows))

i = 0
for col in train_data.columns:
    i = i + 1
    ax = plt.subplot(train_rows,train_cols,i) 
    sns.distplot(train_data[col],fit=stats.norm)
    i = i + 1
    ax = plt.subplot(train_rows,train_cols,i) 
    res = stats.probplot(train_data[col],plot=plt)
plt.tight_layout()
plt.show()

可以看到很多变量都不符合正态分布，所以后面要进行数据变换

接下来看下,KDE图,又名核密度估计图,该图可以查看并对比训练集和测试集中特征变量的分布情况,发现两个数据集中分布不一致的变量,我们来看下V0特征在训练集和测试集中的对比，可以看到，所在集合的分布基本一致

plt.figure(figsize=(8,4),dpi=150)
ax = sns.kdeplot(train_data['V0'],color='Red',shade=True)
ax = sns.kdeplot(test_data['V0'],color="blue",shade=True)
ax.set_xlabel('V0')
ax.set_ylabel("Frequency")
ax = ax.legend(["train","test"])

而对于差距很大的特征会导致模型的泛化能力变差,需要删除此类特征,譬如V5特征

最后我们来看下线性回归关系图,字如其义,主要用来分析变量(特征)之间的线性关系,我们来看下部分特征与target变量之间的关系

# 查看所有特征与target变量之间的线性关系
fcols = 6
frows = len(test_data.columns)
plt.figure(figsize=(5 * fcols,4 * frows))

i = 0
for col in test_data.columns:
    i = i + 1
    ax = plt.subplot(frows,fcols,i) 
    sns.regplot(x=col,y='target',data=train_data,ax=ax,scatter_kws={'marker':'.','s':3,'alpha':0.3},line_kws={'color':'k'});
    plt.xlabel(col)
    plt.ylabel('target')
    i = i + 1
    ax = plt.subplot(frows,fcols,i)
    sns.distplot(train_data[col].dropna())
    plt.xlabel(col)

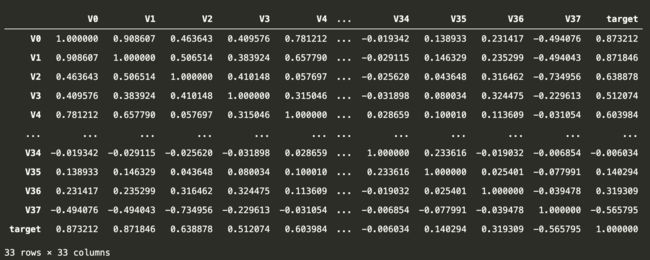
最后来学习下如何确定特征之间的关联性,在删除训练集与数据集中分布不一致的特征后,我们来计算下剩余特征变量及target特征变量之间的相关性系数

# 删除无关的特征变量
pd.set_option('display.max_columns',10)
pd.set_option('display.max_rows',10)
data_train1 = train_data.drop(['V5','V9','V11','V17','V22','V28'],axis = 1)
train_corr = data_train1.corr()
train_corr

为了直观分析,可以使用热力图的形式显示,我们寻找K个与target变量最相关的特征变量，所以我们可以通过热力图筛选出特征变量

# 找出与target相关性最相关的特征 变量
k = 10
cols = train_corr.nlargest(k,'target')['target'].index
cm = np.corrcoef(train_data[cols].values.T)
hm = plt.subplots(figsize=(10,10)) #调整画布大小
hm = sns.heatmap(train_data[cols].corr(),annot=True,square=True)
plt.show()

同理，可以进一步删选出相关系数大于0.5的特征变量

# 筛选出特征变量大于0.5的特征变量
threshold = 0.5
corrmat = train_data.corr()
top_corr_features = corrmat.index[abs(corrmat['target']) > threshold]
plt.figure(figsize=(10,10))
g = sns.heatmap(train_data[top_corr_features].corr(),annot=True,cmap="RdYlGn")

通过这一方法,可以直观筛选出高相关性的系数,相关性系数越大,则认为这些特征变量与target变量的线性影响越大,同时我们可以用相关系数阈值移除相关特征

# 移除相关特征
threshold = 0.5

# 相关系数矩阵
corr_matrix = data_train1.corr().abs()
drop_col=corr_matrix[corr_matrix["target"] < threshold].index 
data_all.drop(drop_col,axis=1,inplace=True)

数据转换

这里要介绍下Box-Cox变换,该变换是统计建模中常用的一种数据转换方法，在连续的响应变量不满足正态分布时，可以使用Box-Cox变换，它可以满足线性回归模型在满足线性，正态性，独立性与方差性的同时，又不丢失信息，可以一定程度上减小不可观测的误差和预测误差的相关性，有利于线性模型的拟合以及分析特征的相关性

在做Box-Cox变换之前，需要对数据进行归一化与处理，在归一化时，对数据进行合并操作使得训练集和测试集分布一致

# Box-Cox变换
drop_columns = ['V5','V9','V11','V22','V28']
# 合并训练集和测试集的数据
train_X = train_data.drop(['target'],axis=1)
data_all = pd.concat([train_data,test_data],axis=0,ignore_index=True)
data_all.drop(drop_columns,axis=1,inplace=True)
data_all.head()

# 对合并后的每列数据进行归一化
cols_numeric=list(data_all.columns)

def scale_minmax(col):
    return (col-col.min()) / (col.max()-col.min())

data_all[cols_numeric] = data_all[cols_numeric].apply(scale_minmax,axis=0)
data_all[cols_numeric].describe()

也可以分开对训练集和测试集进行归一化处理，不过这种处理方式要建立在训练集和测试集分布一致的情况下，建议在数据量大的情况下使用，因为数据量大意味着分布较为一致，数据量较小则会存在分布差异较大的情况，需要在线下进行归一化

train_data_process = train_data[cols_numeric]
train_data_process = train_data_process[cols_numeric].apply(scale_minmax,axis=0)

test_data_process = test_data[cols_numeric]
test_data_process = test_data_process[cols_numeric].apply(scale_minmax,axis=0)

5.3 赛题资料

数据与代码参考地址 https://github.com/zxhjames/tianchi-industrialPredict

更多内容请关注我的公众号"James的黑板报"