NNDL 作业11:优化算法比较
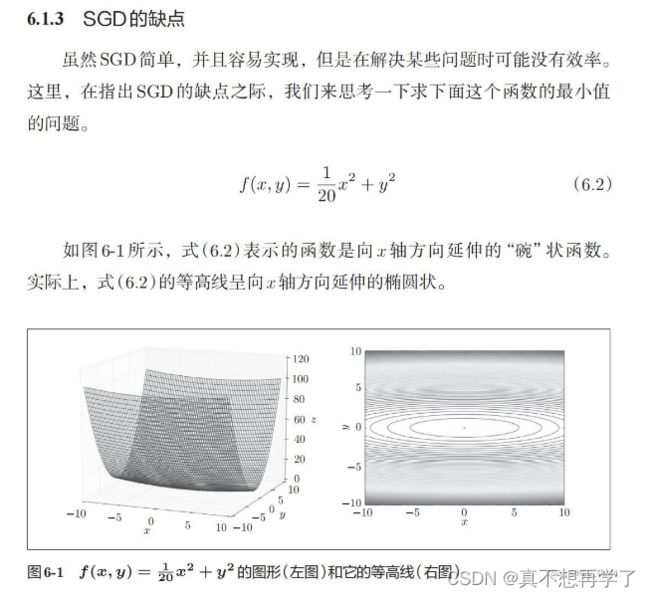
1. 编程实现图6-1,并观察特征
import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# https://blog.csdn.net/weixin_39228381/article/details/108511882
def func(x, y):
return x * x / 20 + y * y
def paint_loss_func():
x = np.linspace(-50, 50, 100) # x的绘制范围是-50到50,从改区间均匀取100个数
y = np.linspace(-50, 50, 100) # y的绘制范围是-50到50,从改区间均匀取100个数
X, Y = np.meshgrid(x, y)
Z = func(X, Y)
fig = plt.figure() # figsize=(10, 10))
ax = Axes3D(fig)
plt.xlabel('x')
plt.ylabel('y')
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='rainbow')
plt.show()
paint_loss_func()
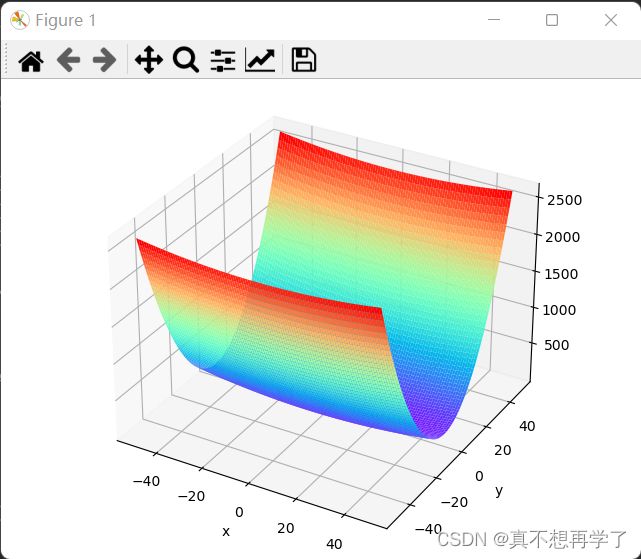

2. 观察梯度方向
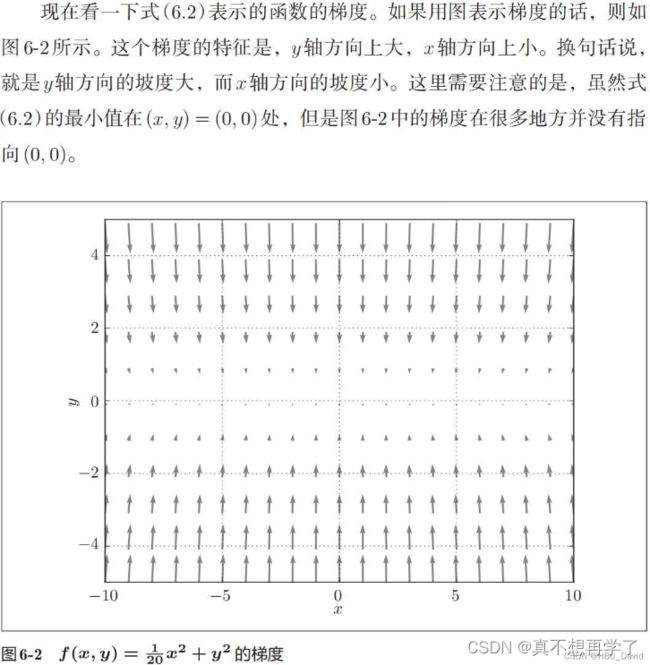
这个就是上面函数俯视角度的梯度方向。箭头长的 地方表示梯度大,短的地方表示梯度小,而且两端的梯度方向明显偏离最优点方向。
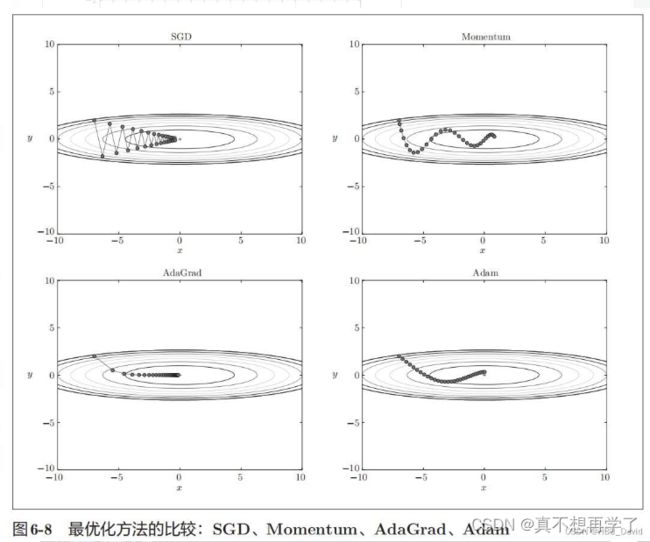
3. 编写代码实现算法,并可视化轨迹
# coding: utf-8
import numpy as np
import matplotlib.pyplot as plt
from collections import OrderedDict
class SGD:
"""随机梯度下降法(Stochastic Gradient Descent)"""
def __init__(self, lr=0.01):
self.lr = lr
def update(self, params, grads):
for key in params.keys():
params[key] -= self.lr * grads[key]
class Momentum:
"""Momentum SGD"""
def __init__(self, lr=0.01, momentum=0.9):
self.lr = lr
self.momentum = momentum
self.v = None
def update(self, params, grads):
if self.v is None:
self.v = {}
for key, val in params.items():
self.v[key] = np.zeros_like(val)
for key in params.keys():
self.v[key] = self.momentum * self.v[key] - self.lr * grads[key]
params[key] += self.v[key]
class Nesterov:
"""Nesterov's Accelerated Gradient (http://arxiv.org/abs/1212.0901)"""
def __init__(self, lr=0.01, momentum=0.9):
self.lr = lr
self.momentum = momentum
self.v = None
def update(self, params, grads):
if self.v is None:
self.v = {}
for key, val in params.items():
self.v[key] = np.zeros_like(val)
for key in params.keys():
self.v[key] *= self.momentum
self.v[key] -= self.lr * grads[key]
params[key] += self.momentum * self.momentum * self.v[key]
params[key] -= (1 + self.momentum) * self.lr * grads[key]
class AdaGrad:
"""AdaGrad"""
def __init__(self, lr=0.01):
self.lr = lr
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] += grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
class RMSprop:
"""RMSprop"""
def __init__(self, lr=0.01, decay_rate=0.99):
self.lr = lr
self.decay_rate = decay_rate
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] *= self.decay_rate
self.h[key] += (1 - self.decay_rate) * grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
class Adam:
"""Adam (http://arxiv.org/abs/1412.6980v8)"""
def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
self.lr = lr
self.beta1 = beta1
self.beta2 = beta2
self.iter = 0
self.m = None
self.v = None
def update(self, params, grads):
if self.m is None:
self.m, self.v = {}, {}
for key, val in params.items():
self.m[key] = np.zeros_like(val)
self.v[key] = np.zeros_like(val)
self.iter += 1
lr_t = self.lr * np.sqrt(1.0 - self.beta2 ** self.iter) / (1.0 - self.beta1 ** self.iter)
for key in params.keys():
self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
self.v[key] += (1 - self.beta2) * (grads[key] ** 2 - self.v[key])
params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)
def f(x, y):
return x ** 2 / 20.0 + y ** 2
def df(x, y):
return x / 10.0, 2.0 * y
init_pos = (-7.0, 2.0)
params = {}
params['x'], params['y'] = init_pos[0], init_pos[1]
grads = {}
grads['x'], grads['y'] = 0, 0
optimizers = OrderedDict()
optimizers["SGD"] = SGD(lr=0.95)
optimizers["Momentum"] = Momentum(lr=0.1)
optimizers["AdaGrad"] = AdaGrad(lr=1.5)
optimizers["Adam"] = Adam(lr=0.3)
idx = 1
for key in optimizers:
optimizer = optimizers[key]
x_history = []
y_history = []
params['x'], params['y'] = init_pos[0], init_pos[1]
for i in range(30):
x_history.append(params['x'])
y_history.append(params['y'])
grads['x'], grads['y'] = df(params['x'], params['y'])
optimizer.update(params, grads)
x = np.arange(-10, 10, 0.01)
y = np.arange(-5, 5, 0.01)
X, Y = np.meshgrid(x, y)
Z = f(X, Y)
# for simple contour line
mask = Z > 7
Z[mask] = 0
# plot
plt.subplot(2, 2, idx)
idx += 1
plt.plot(x_history, y_history, 'o-', color="red")
plt.contour(X, Y, Z) # 绘制等高线
plt.ylim(-10, 10)
plt.xlim(-10, 10)
plt.plot(0, 0, '+')
plt.title(key)
plt.xlabel("x")
plt.ylabel("y")
plt.subplots_adjust(wspace=0, hspace=0) # 调整子图间距
plt.show()
4. 分析上图,说明原理(选做)
为什么SGD会走“之字形”?其它算法为什么会比较平滑?
SGD算法:
随机梯度下降法是对GD的简化,因为SGD在每一步放弃了对梯度准确性的追求,每步仅仅随机采样少量样本来计算梯度。但是这也导致了他的一个很大的缺点就是对导数的梯度采集的不够准确,它只随机采取了样品中的部分梯度代替了所有样本的梯度,所以梯度方向显示出了很强的波动性。
其他的算法:
Momentum、AdaGrad
Momentum动量法是对前几步 的梯度进行加权求和再求平均,也就是说,当前的梯度更新方向不只来自于当前位置的梯度方向,而且前几步的梯度也对当前位置的梯度更新方向有影响,这也就是所谓的移动平均,在此基础上的加权移动平均就是前面说的加权求和再求平均,如果不加权,就是简单的移动平均,实际上权重值改变了对前几步梯度的重视程度。通过这种算法优化了梯度更新方向的波动性。
AdaGrad自适应梯度更新,实际上就是利用一个数学式,对每一步的更新率lr进行调整,

中间那个式子,计算更新值的时候,实际上并没有简单的用学习率 ϵ \epsilon ϵ,而是对更新率进行了调整,式子
ϵ σ + r \frac{\epsilon}{\sigma+\sqrt{r}} σ+rϵ
就是通过r对更新率进行调整,当r很小时,学习率增大,r很大时,学习率减小, σ \sigma σ则是为了防止r为0的情况,通常根据实际情况设一具体值 .
r则来自所有之前梯度的累加,所以它会抑制梯度太大的方向的更新速率,加快梯度较小的方向的更新速率,这样也平滑了更新曲线。
Momentum、AdaGrad对SGD的改进体现在哪里?速度?方向?在图上有哪些体现?
上面说过的就不再重复,补充一点没说过的,
动量法并没有改变参数更新的速率,但是调整了梯度更新的方向和大小,梯度更新的方向和大小,是由前几步的梯度方向和大小决定的,而这种影响程度也可以通过权重分布来调整,
AdaGrad则是仅改变了梯度的更新速率,使得算法在梯度大的地方慢一点更新,在梯度小的地方快一点更新,在具体的当前位置的梯度,更新方向并没有改变。
在图上的表现
动量法的轨迹方向改变不会很剧烈,它倾向于保留之前的梯度更新状态,通常类比与物体的惯性,有质量的物体具有维持自身运动状态的能力,中学物理是这样学的,那么动量法这里就是当前的梯度更新状态(包括方向和大小),倾向于保留前几步的梯度方向和大小。这里面其实还是有挺大区别的,动量法只是模拟一下这种效果,而且算法最好是简单,易计算为主,要完全模拟物体的效果就会增大计算量了。
AdaGrad的轨迹就会很平滑,因为它抑制了梯度大的方向的更新速率,提高了梯度小的方向的更新速率。所以它不会因为梯度偏离最优点而产生较大的波动。
仅从轨迹来看,Adam似乎不如AdaGrad效果好,是这样么?
这是求解问题的过于简单所致。Adam可以看作是 Momentum动量法和AdaGrad自适应梯度更新的结合,它结合了二者的优点于一身,自然会有它的优越性。由于动量法的参与,Adam有一定的保持原来更新梯度方向的倾向,这使得它有一定的逃逸极小值点的能力,在复杂问题上,它有能力脱离极小值点去搜索其他极小值点,这从运行结果中可以看出来。而AdaGrad算法则是径直走向了极小值点,它不能跳出当前的最小值点,缺少了全局搜索最优解的能力,但是我们也不能否认它快速求解局部极小值点的能力。

四种方法分别用了多长时间?是否符合预期?
0.04188799858093262
0.040869951248168945
0.04188966751098633
0.040892839431762695
都比较快,符合预期。
调整学习率、动量等超参数,轨迹有哪些变化?
将学习率在原来基础上分别乘上倍数:[0.5,1,10,50,100]
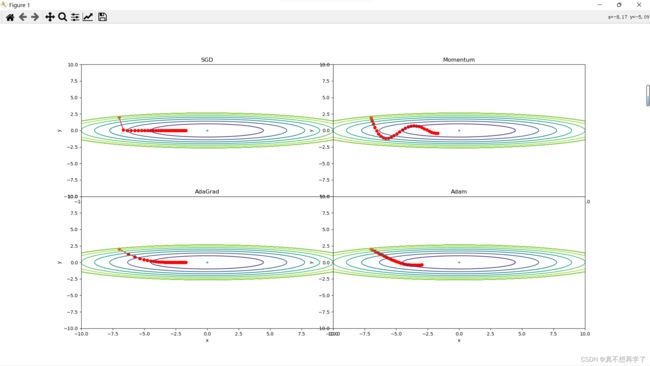

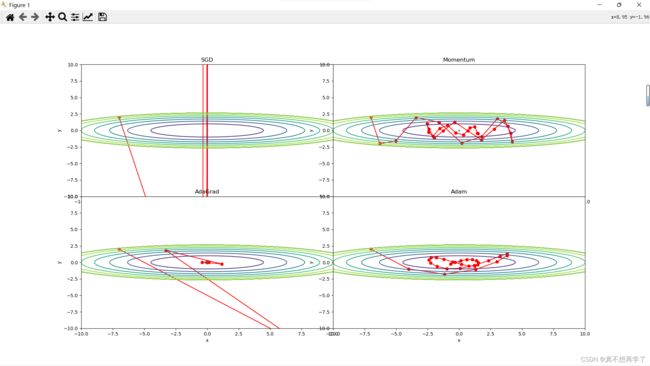
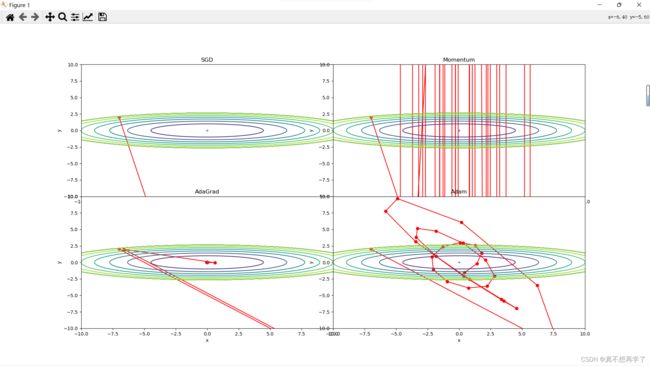
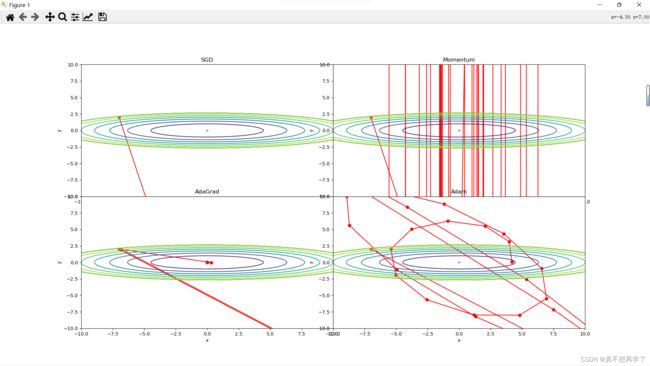
结果让人感觉十分崩坏,当学习率增大到10倍时,就已经开始离谱了起来,梯度过大时,只有Adam还保持着较为优雅的体态,其他的几种都抛出屏幕之外了。而且是只计算了30步,可以看到Adam是波动性最小的,它具有很强的抗干扰能力。
下面是将动量法的动量系数修改分别为:
optimizers["Momentum1"] = Momentum(lr=0.1,momentum=0.1)
optimizers["Momentum2"] = Momentum(lr=0.1,momentum=0.5)
optimizers["Momentum3"] = Momentum(lr=0.1,momentum=0.9)
optimizers["Momentum4"] = Momentum(lr=0.1,momentum=1)
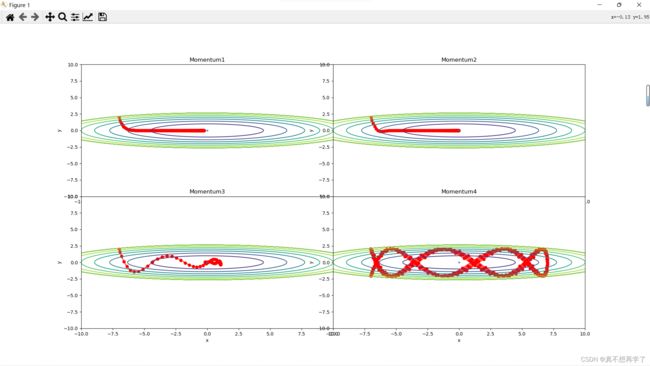
可以看到,当系数较小时,会使得其拉低自身的梯度大小,最后表现出难以移动的感觉。而当系数过大时,会导致其难以停止,当系数达到1时,观察最后那个图,它形成了一种循环的状态。所以0.9~0.999之间的值是优先可取的。
5. 总结SGD、Momentum、AdaGrad、Adam的优缺点(选做)
SGD:
优点:算法简单,缺点:更新梯度时的波动较大,比较不稳定。收敛速度慢
Momentum:
优点:具有一定的稳定性,能跳出鞍点,缺点:梯度过大时会掠过最优点,难以停下。
AdaGrad:
优点:能自己调整学习率,能快速找到局部极小值点。缺点:不能跳出局部极小点,同时容易提前结束搜索,原因是梯度的累积。
Adam:
优点:具有很强的稳定性,有一定的跳出局部极小值点的能力,性能很平均,综合了很多算法 的思想。缺点:过于综合,在特定问题上的求解不如其他算法有优势。
6. Adam这么好,SGD是不是就用不到了?(选做)
不是的,SGD作为经典的优化算法,不仅为其他算法的优化提供了思路,其本身也有其优点,比如梯度计算速度快,由于算法简单,其占用计算空间也是最小的,对于大体量的求解任务,SGD能以比其他算法快的计算速度搜索最优解。
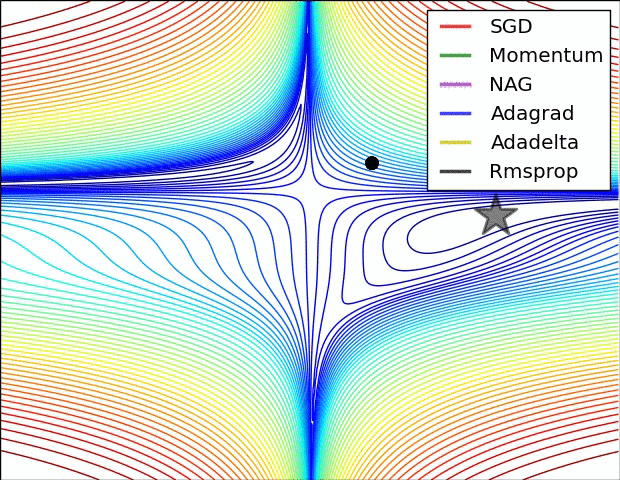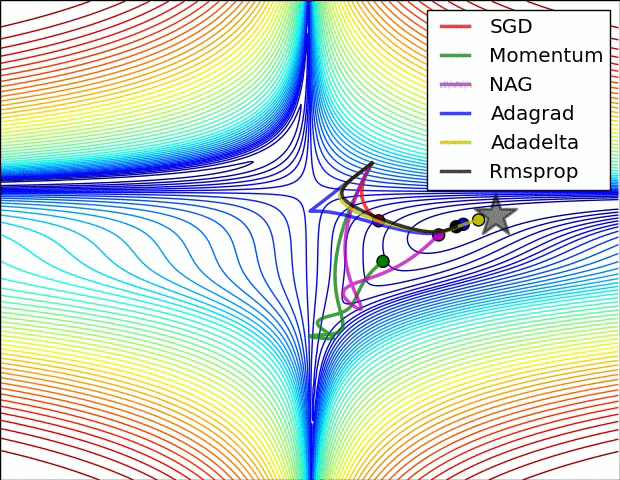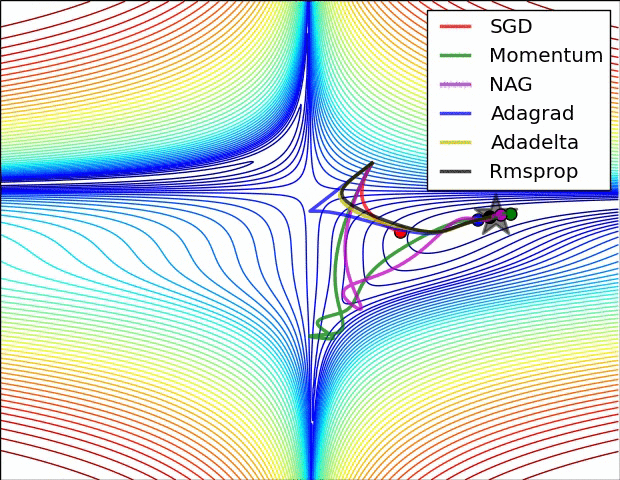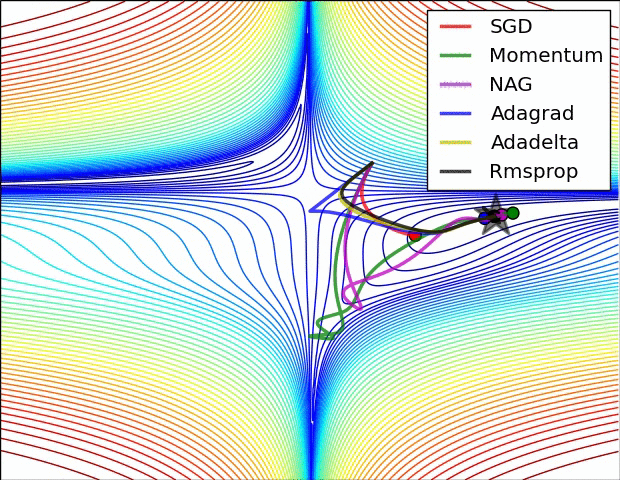
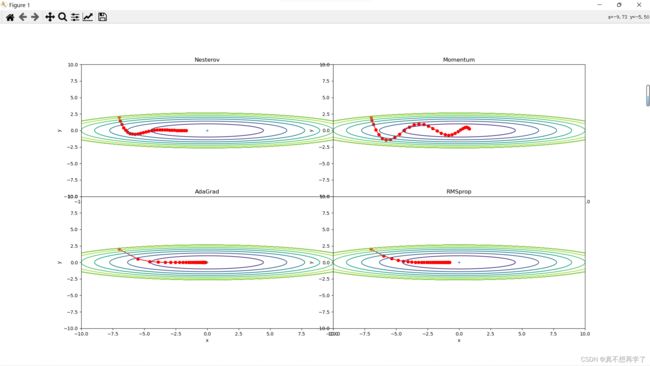
7. 增加RMSprop、Nesterov算法。(选做)
对比Momentum与Nesterov、AdaGrad与RMSprop。
optimizers["Nesterov"] = Nesterov(lr=0.05)
optimizers["Momentum"] = Momentum(lr=0.1)
optimizers["AdaGrad"] = AdaGrad(lr=1.5)
optimizers["RMSprop"] = RMSprop(lr=0.1)
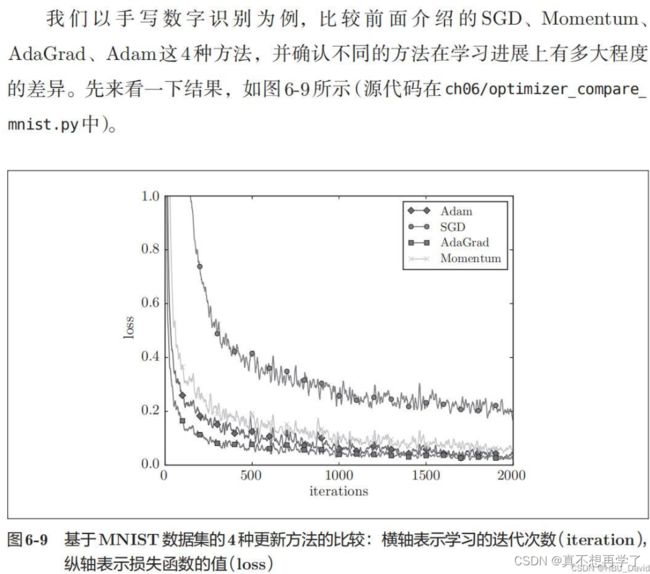
8. 基于MNIST数据集的更新方法的比较(选做)
编程实现,并谈谈自己的看法。
# coding: utf-8
import os
import sys
sys.path.append(os.pardir) # 为了导入父目录的文件而进行的设定
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from common.util import smooth_curve
from common.multi_layer_net import MultiLayerNet
from common.optimizer import *
# 0:读入MNIST数据==========
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)
train_size = x_train.shape[0]
batch_size = 128
max_iterations = 2000
# 1:进行实验的设置==========
optimizers = {}
optimizers['SGD'] = SGD()
optimizers['Momentum'] = Momentum()
optimizers['AdaGrad'] = AdaGrad()
optimizers['Adam'] = Adam()
#optimizers['RMSprop'] = RMSprop()
networks = {}
train_loss = {}
for key in optimizers.keys():
networks[key] = MultiLayerNet(
input_size=784, hidden_size_list=[100, 100, 100, 100],
output_size=10)
train_loss[key] = []
# 2:开始训练==========
for i in range(max_iterations):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
for key in optimizers.keys():
grads = networks[key].gradient(x_batch, t_batch)
optimizers[key].update(networks[key].params, grads)
loss = networks[key].loss(x_batch, t_batch)
train_loss[key].append(loss)
if i % 100 == 0:
print( "===========" + "iteration:" + str(i) + "===========")
for key in optimizers.keys():
loss = networks[key].loss(x_batch, t_batch)
print(key + ":" + str(loss))
# 3.绘制图形==========
markers = {"SGD": "o", "Momentum": "x", "AdaGrad": "s", "Adam": "D"}
x = np.arange(max_iterations)
for key in optimizers.keys():
plt.plot(x, smooth_curve(train_loss[key]), marker=markers[key], markevery=100, label=key)
plt.xlabel("iterations")
plt.ylabel("loss")
plt.ylim(0, 1)
plt.legend()
plt.show()
总结:各个算法都有各自的优缺点,我们可以草率的用综合性最强的Adam算法,也乐意用其他算法进行尝试,因为对于复杂的问题,我们很难直观判断出它究竟适合用哪一种优化算法,所以对于优化算法的选择,一方面需要对每一种算法的原理有着较为深刻的理解,另一方面也需要很长时间的经验积累才行。
comeform:
https://blog.csdn.net/qq_38975453/article/details/128025693?spm=1001.2014.3001.5502
ref:
https://zhuanlan.zhihu.com/p/90169812
https://blog.csdn.net/qq_32907491/article/details/107442503