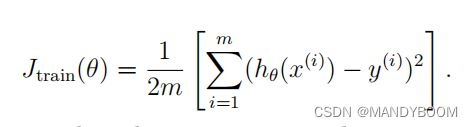第06周:吴恩达机器学习课后编程题ex5方差偏差——Python
在本练习中,您将实现正则化线性回归并将其用于研究具有不同偏差方差特性的模型。
1 Regularized Linear Regression正则化线性回归
在练习的前半部分,您将使用正则化线性回归从流出大坝的水量预测水库中的水位。 在下半部分,您将完成一些调试学习算法的诊断,并检查偏差与方差的影响。
1.1 Visualizing the dataset 可视化数据集
该数据集分为三个部分:
• 您的模型将学习的训练集:X, y
• 用于确定正则化参数的交叉验证集: Xval,yval
• 用于评估性能的测试集:Xtest、ytest
训练集用来训练,验证集用来进行模型(参数)的选择,测试集用来看模型的泛化能力。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from IPython.core.pylabtools import figsize
from scipy.io import loadmat
data = loadmat('ex5data1.mat')
# 训练集
X = data['X'] # (12,1)
y = data['y'] # (12,1)
# print(X.shape, y.shape)
# 交叉验证集
X_val = data['Xval'] # (21, 1)
y_val = data['yval'] # (21, 1)
# print(X_val.shape, y_val.shape)
# 测试集
X_test = data['Xtest'] # (21, 1)
y_test = data['ytest'] # (21, 1)
# print(X_test.shape, y_test.shape)
X = np.insert(X, 0, 1, axis=1) # (12, 2)
X_val = np.insert(X_val, 0, 1, axis=1) # (21, 2)
X_test = np.insert(X_test, 0, 1, axis=1) # (21, 2)
# print(X.shape, X_val.shape, X_test.shape)
#作图
fig,ax = plt.subplots(figsize=(12, 8))
ax.scatter(data['X'], data['y'], label = 'training data')
ax.set_xlabel('change in water level X')
ax.set_ylabel('water flowing out of the dam y')
plt.show()1.2 Regularized linear regression cost function
正则化线性回归代价函数
使用一个正则化线性回归函数来拟合上面的数据,正则化线性回
归具有以下代价函数:
# 定义正则化线性回归代价函数
def reg_cost(theta, X, y, lam):
error = X @ theta - y.flatten()
first_part = 1 / (2 * len(X)) * np.sum(np.power(error, 2))
reg = lam / (2 * len(X)) * np.sum(np.power(theta[1:], 2))
return first_part + reg1.3 Regularized linear regression gradient正则化线性回归梯度
相应地,正则化线性回归代价的偏导数 对于 θj 定义为
对j=0那一项不惩罚
# 定义正则化线性回归代价的偏导数
def reg_gradient(theta, X, y, lam):
error = X @ theta - y.flatten()
first_part = X.T @ error/len(X)
reg = (lam / len(X)) * theta
reg[0] = 0
return first_part + reg1.4 Fitting linear regression 拟合线性回归
先算出参数θ,在这一部分中,我们将正则化参数 λ 设置为0。因为我们的线性回归的当前实现是试图拟合二维θ,正则化对于如此低维度的 θ 不会有太大的帮助。
# 定义训练过程
from scipy.optimize import minimize
def train(X, y, lam):
theta = np.ones(X.shape[1])
res = minimize(fun=reg_cost,x0=theta,args=(X,y,lam),method='TNC',jac=reg_gradient)
return res.x
theta = train(X, y, lam = 0)
print(theta)得到θ:[13.08790348 0.36777923]
绘制拟合图线,发现拟合的并不是很好,偏差bias很大
#画出拟合曲线
x = np.linspace(-50, 50, 100)
f = theta[0] + theta[1]*x
fig, ax = plt.subplots(figsize=(12,8))
ax.scatter(data['X'], data['y'], label='training data')
ax.plot(x, f, 'blue')
ax.set_xlabel('change in water level x')
ax.set_ylabel('water flowing out of the dam y')
plt.show()2 Bias-variance偏差方差
机器学习中的一个重要概念是偏差-方差权衡。具有高偏差的模型对于数据来说不够复杂并且容易欠拟合, 而对训练数据具有高方差的模型容易过拟合。
这一部分画出训练集和验证集的学习曲线来观察偏差、方差情况。
2.1 Learning curves 学习曲线
训练样本X从1开始逐渐增加,训练出不同的参数向量θ。接着通过交叉验证样本Xval计算验证误差。
1、使用训练集的子集来训练模型,得到不同的theta。
2、通过theta计算训练代价和交叉验证代价,切记此时不要使用正则化,将 λ=0。
3、计算交叉验证代价时记得整个交叉验证集来计算,无需分为子集。
训练集的平均误差平方和定义为:
# 求出训练集误差和交叉验证集误差以绘制学习曲线
def plot_learningcurve(X, y, X_val, y_val, lam):
x = range(1, X.shape[0]+1)
traincosts=[] # 训练集误差的数组
valcosts=[] # 交叉验证集误差的数组
for i in x:
theta_s = train(X[:i,:],y[:i,:],lam) # 用训练集算出θ
trainingcost = reg_cost(theta_s, X[:i,:],y[:i,:],lam)
valcost = reg_cost(theta_s, X_val, y_val ,lam) # 用整个交叉验证集计算验证集误差
traincosts.append(trainingcost)
valcosts.append(valcost)
plt.plot(x, traincosts, label='training cost')
plt.plot(x, valcosts, label='val cost')
plt.legend()
plt.xlabel('number of training examples')
plt.ylabel('error')
plt.show()
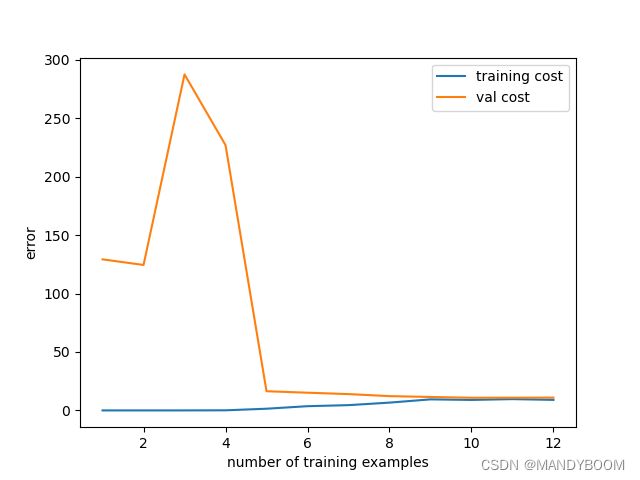
lam = 0
plot_learningcurve(X, y, X_val, y_val,lam)当训练样本数量增大到一定数量后,误差变化很微小了,这是高偏差问题,对于高偏差问题,解决办法:①采用多项式特征 ②减小正则化参数 由于此例中λ=0,所以不能再减小了,所以采用多项式特征。
3 Polynomial regression多项式回归
对于使用多项式回归,我们的假设具有以下形式:
![]()
先为样本增加多项式特征:
# 增加多项式特征
def feature(X, power):
for i in range(2, power+1):
X = np.insert(X,X.shape[1],np.power(X[:,1],power),axis=1)
return X不同特征具有不同量级时会导致:a.数量级的差异将导致数量级大的特征占据主导地位;b.数量级的差异将导致迭代收敛速度变慢。所以需要对X归一化:所有数据集应该都用训练集的均值和样本标准差处理。
# 先求训练集均值和标准差
def get_mean_std(X):
means = np.mean(X,axis=0) # 按列求均值
stds = np.std(X,axis=0) # 按列求标准差
return means, stds
# 归一化
def feature_normalize(X, means, stds):
X[:,1:] = (X[:,1:]-means[1:])/stds[1:]
return Xpower = 8
X_poly = feature(X, power)
X_val_poly = feature(X_val, power)
X_test_poly = feature(X_test, power)
train_means, train_stds = get_mean_std(X_poly)
X_norm = feature_normalize(X_poly, train_means, train_stds)
X_val_norm = feature_normalize(X_val_poly,train_means, train_stds)
X_test_norm = feature_normalize(X_test_poly,train_means, train_stds)
theta_fit = train(X_norm, y, lam=0)然后画出拟合图像,此时多项式power=8
# 再次画出拟合图像
def plot_poly_fit():
x = np.linspace(-50,50,100)
x_final = x.reshape(100,1)
x_final = np.insert(x_final, 0, 1,axis=1)
x_final = feature(x_final,power)
x_final = feature_normalize(x_final,train_means,train_stds)
fig,ax = plt.subplots(figsize=(12,8))
ax.scatter(data['X'], data['y'], label = 'Training Data')
ax.plot(x, x_final@theta_fit,'yellow')
ax.set_xlabel('change in water level x')
ax.set_ylabel('water flowing out of the dam y')
plt.show()
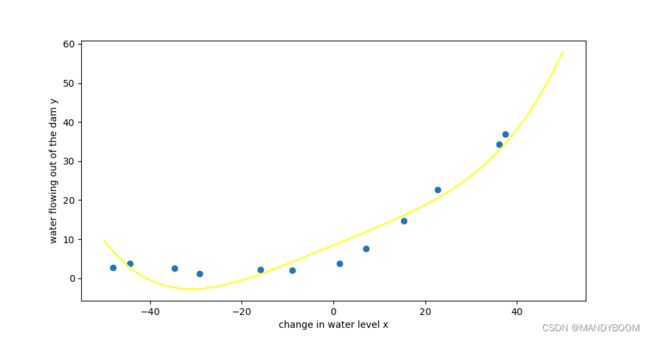
plot_poly_fit()再画出学习曲线:
但是我觉得图像拟合的不是很好,所以我又尝试了power=4,拟合的会稍微好一些,学习曲线(验证集误差)也不是先增大后减小了,但是还是没有题目中给出的最后的效果好。