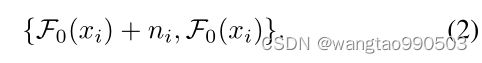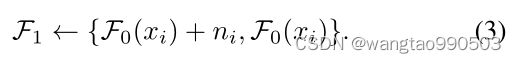IDR:通过迭代数据细化的自我监督图像去噪
本文是CVPR2022的新论文,因与我的研究方向不是紧密相关,所以不看前两节,直接上方法!
方法
在本节中,作者首先介绍了噪声数据集的创建,在此基础上,对使用噪声数据集进行学习去噪进行了研究,并实证验证了两个发现。然后,作者展示了他的自我监督去噪框架:迭代数据细化(IDR)。为了加速这种迭代方法的训练过程,作者进一步引入了一个快速版本的 IDR 以减少训练时间,同时获得与 IDR 完整版本相似的性能。
1. 学习去噪的数据偏差试点研究(Pilot Study on Data Bias of Learning Denoising)
对于使用已知噪声模型训练去噪模型,一种典型的方法 [37] 是通过将噪声 n 添加到地面真实干净图像 y 上来创建合成噪声图像,表示为 y + n 并用作网络输入。我们将此类合成训练数据命名为噪声-清洁数据集,用于学习映射 (y + n) → y。
然而,真实的干净图像 y 通常很难获得。另一种似是而非的方法是将噪声 n 添加到实际的噪声图像 x 上,以创建噪声更均匀的图像 x + n,其中较晚的噪声 x + n 被视为输入,而前噪声图像 x 被用作学习目标。我们将此类训练数据称为噪声更大的数据集(noisier-noisy dataset)。
虽然后面的数据集更容易获得,但上述两类数据集之间不可避免地存在数据偏差,并且在后面的 noisier-noisy 数据集上训练的去噪网络不能很好地处理实际的噪声图像 x。我们进行如下试点研究,并凭经验验证两个重要发现。形式上,数据集表示为:
这里,![]() 是一张干净的图像(实际上很难获得),
是一张干净的图像(实际上很难获得),![]() =
= ![]() +
+ ![]() 是其对应的噪声图像,
是其对应的噪声图像,![]() 是噪声模型产生的随机噪声,
是噪声模型产生的随机噪声,![]() +
+![]() 表示应用采样噪声
表示应用采样噪声 ![]() 到实际嘈杂的图像
到实际嘈杂的图像 ![]() 以创建合成的但更嘈杂的图像。为简单起见,我们分别用 {
以创建合成的但更嘈杂的图像。为简单起见,我们分别用 {![]() +
+ ![]() ,
, ![]() } 和 {
} 和 {![]() +
+ ![]() ,
, ![]() } 表示 {(
} 表示 {(![]() +
+![]() ,
, ![]() )}
)}![]() 和 {(
和 {(![]() +
+![]() ,
, ![]() )}
)}![]() 。
。
为了分析使用噪声较大的数据集训练网络的数据偏差,我们在噪声干净和噪声较大的数据集上从头开始训练 U-Net,并研究三种代表性噪声类型:原始图像、高斯噪声和相关噪声,具有各种噪音水平。它们涵盖了常见的噪声类型,即信号相关/信号无关噪声和逐点/相关噪声。噪声模型的更多设置可以在图 2 的标题中找到。为了测试,我们从训练噪声水平中均匀地采样 4 个离散噪声水平,并在实际的噪声-干净图像对上测试去噪模型,这些图像对具有真实性。
 图2. 用噪声干净的数据集和三种代表性噪声和一系列噪声水平的噪声较大的数据集训练的去噪网络的去噪性能。对于高斯噪声和相关噪声,我们分别从 [5, 20] 和 [2, 5] 中统一采样它们的噪声水平。对于真实世界的原始图像噪声*,我们使用 HUAWEI Mate20 的噪声轮廓,可以建模为泊松-高斯噪声模型,并从 [800, 3200] 中均匀采样 ISO。 *这里,“真实世界的原始图像噪声”是在泊松-高斯噪声模型的假设下。
图2. 用噪声干净的数据集和三种代表性噪声和一系列噪声水平的噪声较大的数据集训练的去噪网络的去噪性能。对于高斯噪声和相关噪声,我们分别从 [5, 20] 和 [2, 5] 中统一采样它们的噪声水平。对于真实世界的原始图像噪声*,我们使用 HUAWEI Mate20 的噪声轮廓,可以建模为泊松-高斯噪声模型,并从 [800, 3200] 中均匀采样 ISO。 *这里,“真实世界的原始图像噪声”是在泊松-高斯噪声模型的假设下。
如图 2 所示,对各种噪声类型和噪声水平的训练显示出一致的结果,这导致了以下两个发现:
- 在相同的噪声模型中,用噪声较大的数据集训练的去噪网络可以对实际的噪声图像(图 2 中的红色与蓝色的点)进行去噪。
- 使用相同的噪声模型,在偏差较小的数据集上向理想的噪声-干净数据集进行训练有助于去噪网络实现更好的去噪性能(表 1)。
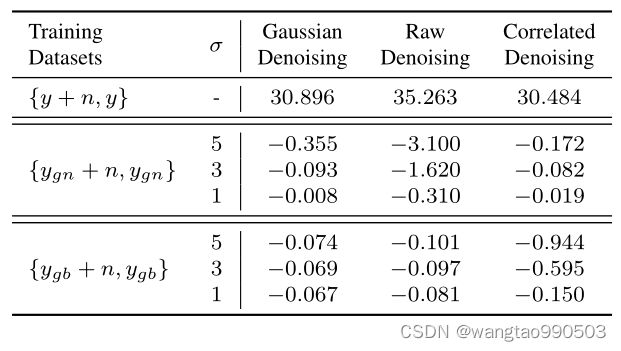 表1. 使用具有不同强度的有偏数据集训练的模型的去噪性能。我们通过应用具有不同强度 (σ) 的高斯噪声或高斯模糊来破坏干净的目标,以创建有偏差的目标 (y_gn & y_gb),并添加三种不同类型的噪声以创建输入噪声较大的图像 (y_gn + n & y_gb + n)。最后六行显示了当模型使用不同的偏差数据集训练到理想的噪声干净数据集(第一行)时,PSNR 下降。
表1. 使用具有不同强度的有偏数据集训练的模型的去噪性能。我们通过应用具有不同强度 (σ) 的高斯噪声或高斯模糊来破坏干净的目标,以创建有偏差的目标 (y_gn & y_gb),并添加三种不同类型的噪声以创建输入噪声较大的图像 (y_gn + n & y_gb + n)。最后六行显示了当模型使用不同的偏差数据集训练到理想的噪声干净数据集(第一行)时,PSNR 下降。
对于第一个发现,使用噪声更大数据集(图 2 中的红点)训练的模型在所有噪声类型上始终显示比没有任何去噪的实际噪声图像(图 2 中的蓝点)更好的 PSNR,这表明该模型即使在噪声和噪声-干净的数据集之间存在数据偏差,也可以在一定程度上对实际噪声图像 {xi} 进行去噪。最近,基于单图像的和基于批处理的方法都对高斯噪声得出了类似的结论,但它们只研究单个噪声水平。我们的调查扩大了他们的观察范围,涵盖了更广泛的噪音类型和噪音水平。
对于第二个发现,我们首先删除了噪声较大的数据集中的所有数据偏差,它变成了一个噪声-干净的数据集(零数据偏差)。基于它训练的模型被认为在所有三种噪声类型和不同的噪声水平上都具有最佳性能(图 2 中的绿点)。然后我们综合不同类型和强度的数据偏差来进一步验证第二个发现。具体来说,我们应用不同级别的高斯噪声或高斯模糊(在表 1 中表示为 σ)来污染干净的图像 y 以创建有偏差的目标(表示为 ![]() 和
和 ![]() )。将上述具有不同噪声水平的相同三个噪声模型(高斯、原始、相关)进一步添加到偏置目标中,以创建噪声图像(
)。将上述具有不同噪声水平的相同三个噪声模型(高斯、原始、相关)进一步添加到偏置目标中,以创建噪声图像(![]() + n 和
+ n 和 ![]() + n)作为网络训练的输入。使用不同强度的有偏数据集训练单独的去噪网络,并在同一噪声模型的实际噪声图像上进行测试。表 1 中的结果表明,在具有较小数据偏差(表 1 中较小的 σ)的数据集上训练的去噪网络显示出更好的去噪性能,第二个发现对于两种类型的数据偏差、三种不同的噪声类型和三种噪声级别是一致的(3 × 2 × 3 = 18 个单独的去噪网络被训练和评估)。
+ n)作为网络训练的输入。使用不同强度的有偏数据集训练单独的去噪网络,并在同一噪声模型的实际噪声图像上进行测试。表 1 中的结果表明,在具有较小数据偏差(表 1 中较小的 σ)的数据集上训练的去噪网络显示出更好的去噪性能,第二个发现对于两种类型的数据偏差、三种不同的噪声类型和三种噪声级别是一致的(3 × 2 × 3 = 18 个单独的去噪网络被训练和评估)。
2. 迭代数据细化
第 3.1 节中的两个发现启发我们迭代地减少嘈杂噪声数据集和理想噪声干净数据集之间的数据偏差。逐渐创建偏差较小的数据集并对其进行训练会带来有希望的去噪性能。
我们首先基于初始噪声数据集 {![]() +
+ ![]() ,
, ![]() }训练模型
}训练模型 ![]() 。根据我们在 3.1 节中的发现 1,它可以在一定程度上对实际的噪声图像 {
。根据我们在 3.1 节中的发现 1,它可以在一定程度上对实际的噪声图像 {![]() } 进行去噪。因此,我们可以用它对噪声图像进行去噪,得到一组新的精炼训练数据集:
} 进行去噪。因此,我们可以用它对噪声图像进行去噪,得到一组新的精炼训练数据集:
新构建的数据集与原始噪声较大的数据集 {![]() +
+ ![]() ,
, ![]() }共享相同数量的图像和内容。然而,这个新数据集对噪声干净数据集的数据偏差较小,因为我们训练的去噪模型
}共享相同数量的图像和内容。然而,这个新数据集对噪声干净数据集的数据偏差较小,因为我们训练的去噪模型 ![]() 减少了目标的 L2 距离(根据我们在第 3.1 节中的发现 1)。
减少了目标的 L2 距离(根据我们在第 3.1 节中的发现 1)。
然后,使用上面的偏差较小的数据集构造,我们可以在下一轮从头开始训练一个新的去噪模型 ![]()
由于新数据集 {![]() +
+ ![]() ,
, ![]() } 和理想的噪声干净数据集 {
} 和理想的噪声干净数据集 {![]() +
+ ![]() ,
, ![]() } 之间的数据偏差得到缓解,根据我们在第 3.1 节中的发现 2,训练模型与在第一轮噪声较大的数据集上训练的
} 之间的数据偏差得到缓解,根据我们在第 3.1 节中的发现 2,训练模型与在第一轮噪声较大的数据集上训练的 ![]() 相比,
相比,![]() 可以更好地泛化到实际噪声图像 {
可以更好地泛化到实际噪声图像 {![]() }。
}。
基于改进的模型 ![]() ,上述过程可以通过细化训练目标和训练更好的模型来迭代交替执行,如图 3 所示。从模型的角度来看,一旦我们有了一个去噪模型
,上述过程可以通过细化训练目标和训练更好的模型来迭代交替执行,如图 3 所示。从模型的角度来看,一旦我们有了一个去噪模型 ![]() ,一个更好的模型
,一个更好的模型 ![]() 可以使用构建的数据集进行训练:
可以使用构建的数据集进行训练:
先前的模型 ![]() 有助于缩小新的噪声较大的数据集 {
有助于缩小新的噪声较大的数据集 {![]() +
+ ![]() ,
, ![]() } 和理想的噪声干净的数据集 {
} 和理想的噪声干净的数据集 {![]() +
+ ![]() ,
, ![]() }之间的差距。在下一轮训练中,新创建的噪声数据集的改进使得我们新训练的模型
}之间的差距。在下一轮训练中,新创建的噪声数据集的改进使得我们新训练的模型 ![]() 的推进。另一方面,从目标的角度来看,中间去噪模型会产生一系列中间细化目标 {
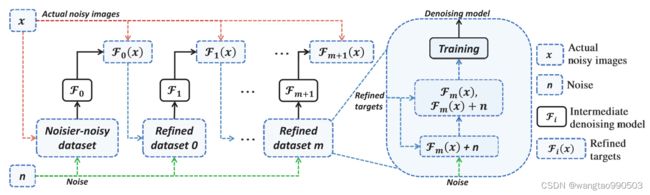
的推进。另一方面,从目标的角度来看,中间去噪模型会产生一系列中间细化目标 {![]() }(对于 m = 0, 1, ...)。如图 1 所示,训练目标上的噪声被去除,更多的纹理被逐步恢复。此外,与传统的迭代方法多次对一张噪声图像去噪并导致大量纹理丢失不同,我们的方法在推理过程中改进了训练数据集并对噪声图像进行了一次去噪。
}(对于 m = 0, 1, ...)。如图 1 所示,训练目标上的噪声被去除,更多的纹理被逐步恢复。此外,与传统的迭代方法多次对一张噪声图像去噪并导致大量纹理丢失不同,我们的方法在推理过程中改进了训练数据集并对噪声图像进行了一次去噪。
3. 快速迭代数据细化
虽然上述迭代数据细化不会增加推理(预测)的时间成本,但其训练时间与提议的自监督数据细化的轮数成正比。为了减轻沉重的训练时间成本,我们进一步提出了一种快速近似训练方案。整个算法如算法 1 所示。
我们在两个方面近似我们的完整方法。
首先,我们引入一个epoch的训练,它在每个epoch之后执行一轮数据细化。具体来说,对于每个新构建的数据集,我们只用它来训练我们的模型一个epoch,而不是像以前那样训练它直到完全收敛。在下一个 epoch,我们基于新构建的数据集训练去噪网络。我们牺牲了完整模型优化所需的时间,但增加了数据细化的迭代轮次。我们引入的开销是在每个训练时期之前产生细化的目标。它花费的总训练时间不到 5%。结果,总训练时间减少到几乎与只训练一轮去噪模型相同。
其次,在每个 epoch 对新数据集进行训练时,我们的模型由前一个 epoch 的模型初始化,而不是从头开始。这种累积训练策略有助于去噪网络与所提出的快速数据细化方案更快地收敛,并确保最终去噪模型在整个训练过程中不断优化。近似算法也快速收敛并保持与我们的完整算法相似的性能。
实验
实验我就是大体扫了一下,效果的SSIM大概在0.9上下对不同数据集有所不同。感兴趣的读者可以自行阅读。