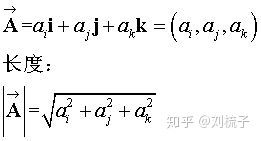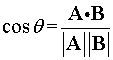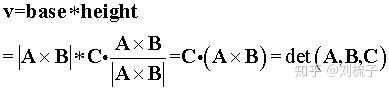向量的点乘和叉乘

点乘，也叫数量积。结果是一个向量在另一个向量方向上投影的长度，是一个标量。

叉乘，也叫向量积。结果是一个和已有两个向量都垂直的向量（法向量）。

点乘在数学中一般用来判断两个向量是否垂直。也可以用来计算一个向量在某个方向上的投影长度，就像定义一样。

叉乘更多的是判断某个平面的方向。从这个平面上选两个不共线的向量，叉乘的结果就是这个平面的法向量。

向量：既有方向又有大小的量

通常情况下会将向量放到坐标系中，常用的是笛卡尔坐标系，向量起始点通常放到原点（注：没有固定的起点，只要方向相同，大小相等，就认为两向量是相同的，但为了用数值坐标来表示向量，将起始点放到原点），因此，三维向量

可以写成如下形式：

1.1向量加法

：

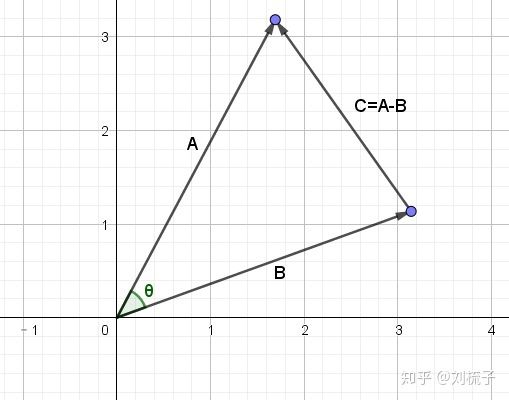
几何图形：

用坐标值

进行相加（从图中可以看出，分别是两向量坐标值的相加）：

1.2向量减法

：

定义了加法，减法很显然了，比如上图中，

1.3向量数乘（向量的伸缩，如果a为负，代表反向）：

1.4 点积（对应元素相乘相加）

结果是一个数！

几何意义：投影

为什么数值计算的结果就代表几何上的投影呢？

利用余弦定理

：

2.点乘应用

2.1计算长度和角度

利用点积找角度很简单，这里就不举例了。

2.2检测正交性

当角度为90度时，即点积为0时，两个向量正交。

举例：满足x+2y+3z=0的点组成的图形是？

答：是一个平面，向量(x,y,z)与向量(1,2,3)正交，因此组成一个过原点的平面，向量(1,2,3)是其法向量。

2.3 求三角形面积

问题：求任给多边形的面积，多边形给出了每个定点坐标

？

答案：先把所有的多边形分解成多个三角形，然后只要能求出三角形面积，问题就解决了。

行列式代表向量组成平行四边形

的面积，因此给出了三角形两边边坐标，便得到了三角形面积。

3.叉积

定义：

意义：叉乘结果是一个向量，向量模长是向量A，B组成平行四边形的面积；向量方向是垂直于向量A,B组成的平面；
 

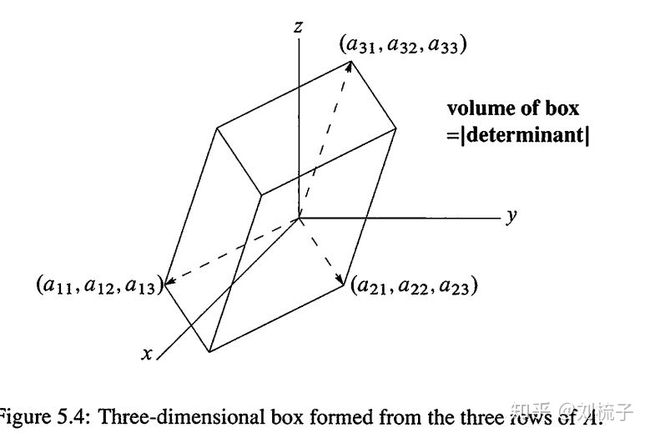
3.1.再看三维空间体积
 

有三个三维向量分别为A,BC，则体积为：

在三维空间中，行列式的含义是体积，因此可以通过求行列式求三维空间的体积。
 

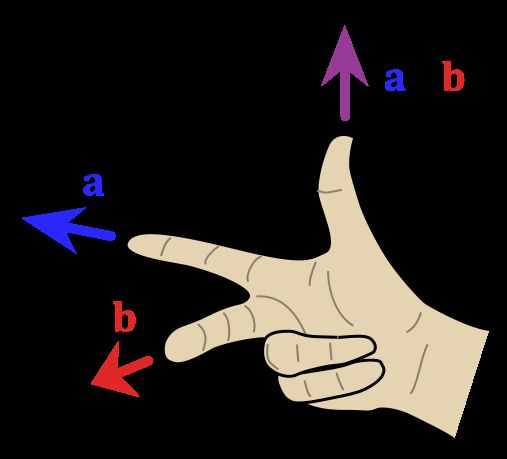
（1）既然叉乘的结果是和两个向量都垂直的向量，那么怎么判断生成向量的方向？

方向的判定采用右手法则

，如下图：

叉乘向量方向的判断(Wiki)

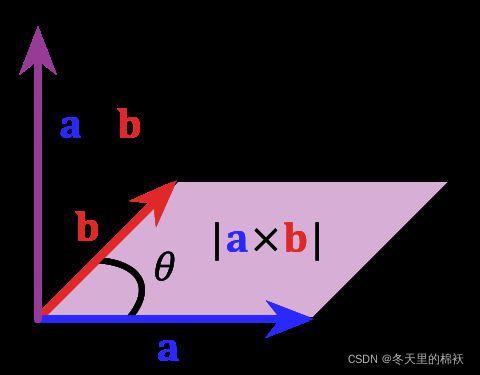
(2)叉乘向量模的大小及其几何意义？

叉乘向量的模

模的几何意义为其对应于由这两天向量组成的平行四边形的面积：

叉乘向量的模（Wiki）

（3）叉乘和点乘的应用举例：

1.判断两个线段是否相交

可以用点乘和叉乘来进行判断，这可以应用于星载激光高度计测高剖面进行交叉点

的查找和最小二乘平差，从而降低轨道误差

，定向误差，和计时误差等的影响。

具体过程总结如下:

Step 1: 快速排斥

即判断以两线段为对角线的矩形是否相交，若不相交，则两线段一定不相交。而判断两个矩形是否相交，如果任一矩形的最右端都大于另一矩形的最左端且任一矩形最高端大于另一矩形的最低端，那么矩形相交；反之，只要其中任一条件不满足，两矩形不相交。经过这一步之后可以将大部分不符合条件的线段排除掉。

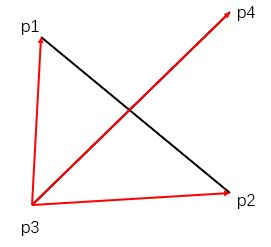
Step 2: 判断两线段是否相交

如果两线段相交，则两线段必须互相跨立对方，即其中任一线段的两端一定在另一线段的两侧 。

判断线段P1P2与P3P4相交（CSDN）

如上图所示：线段P1P2与线段P3P4相交，则P1和P2一定在线段P3P4的两侧，所以有（P3P1 × P3P4）· （P3P1 × P3P4）< 0；同理如果P3和P4在线段P1P2两侧那么有（P2P3 × P2P1）· （P2P4 × P2P1）< 0：如果同时满足以上两条那么就可以证明线段P1P2与线段P3P4相交。

转载链接