MonoSDF学习笔记
MonoSDF: Exploring Monocular Geometric Cues for Neural Implicit Surface Reconstruction NeRF-SLAM: Real-Time Dense Monocular SLAM with Neural Radiance Fields
主页:https://niujinshuchong.github.io/monosdf/
论文:https://arxiv.org/pdf/2206.00665.pdf
Code:https://github.com/autonomousvision/monosdf
效果:
摘要
In recent years, neural implicit surface reconstruction methods have become popular for multi-view 3D reconstruction. In contrast to traditional multi-view stereo methods, these approaches tend to produce smoother and more complete reconstructions due to the inductive smoothness bias of neural networks. State-of-the-art neural implicit methods allow for high-quality reconstructions of simple scenes from many input views. Yet, their performance drops significantly for larger and more complex scenes and scenes captured from sparse viewpoints. This is caused primarily by the inherent ambiguity in the RGB reconstruction loss that does not provide enough constraints, in particular in less-observed and textureless areas. Motivated by recent advances in the area of monocular geometry prediction, we systematically explore the utility these cues provide for improving neural implicit surface reconstruction. We demonstrate that depth and normal cues, predicted by general-purpose monocular estimators, significantly improve reconstruction quality and optimization time. Further, we analyse and investigate multiple design choices for representing neural implicit surfaces, ranging from monolithic MLP models over single-grid to multi-resolution grid representations. We observe that geometric monocular priors improve performance both for small-scale single-object as well as large-scale multi-object scenes, independent of the choice of representation.
译文:
近年来,神经隐式曲面重建方法在多视点三维重建中得到了广泛的应用。与传统的多视点立体方法相比,由于神经网络的诱导平滑偏差,这些方法倾向于产生更平滑和更完整的重建。最先进的神经隐式方法允许从许多输入视图高质量地重建简单场景。然而,对于更大和更复杂的场景以及从稀疏视点捕获的场景,它们的性能显著下降。这主要是由RGB重建损失中的固有模糊性引起的,其没有提供足够的约束,特别是在较少观察和无纹理的区域中。受单眼几何预测领域最新进展的启发,我们系统地探索了这些线索为改善神经隐式表面重建提供的效用。我们证明,深度和正常线索,预测通用单目估计器,显着改善重建质量和优化时间。此外,我们分析和研究了多种设计选择来表示神经隐式表面,范围从单网格上的单片MLP模型到多分辨率网格表示。我们观察到,几何单眼先验无论对于小规模的单对象还是大规模的多对象场景都能提高性能,而与表示的选择无关。
文章工作
贡献:
- 介绍MonoSDF,一个新的框架,它利用单眼几何线索提高多视点三维重建质量,效率,和可伸缩性的神经隐式曲面模型。
- 提供一个系统的比较和详细分析神经隐式曲面表示的设计选择,包括普通的MLP和基于网格的方法。
- 我们在多个挑战进行大量实验数据集,从对象级重建系统数据集[1],在room-level重建[67]复制品和ScanNet[13],在坦克和大规模的室内场景重建寺庙[34]。
工作
- 用于神经隐式场景表示的架构部分:在本文中,提供了一个四种体系结构设计选择的隐式表面重建的系统比较。
- 多视点图像的三维重建部分:在这项工作中表明,合并单眼先验允许这些方法获得更详细的重建和规模更大、更有挑战性的场景。
- 将先验整合到神经场景表示部分:整合了单目深度线索,并进一步证明了单目线索对各种神经场景表示的有效性,范围从MLP到多分辨率特征网格。
算法框架
我们使用通用预训练网络预测的单目几何线索来指导神经隐式曲面模型的优化。更具体地说,对于一批射线,我们将渲染预测的RGB颜色、深度和法线,并优化关于输入RGB图像和单眼几何线索。进一步,我们研究了神经隐式架构的不同设计选择,并提供了深入的分析。
Related Work
Architectures for Neural Implicit Scene Representations
- 神经隐式场景表示或神经场[78](Neural fields in visual computing and beyond)由于其表现力和低内存占用,最近在表示3D几何图形方面获得了普及。
- 初步工作[9,42,50](Learning implicit fields for generative shape modeling、Occupancy networks:Learning 3d reconstruction in function space、Deepsdf: Learning continuous signed distance functions for shape representation)使用单个MLP作为场景表示,并显示出令人印象深刻的对象级重建质量,但由于有限的模型容量,它们不能缩放到更复杂或大规模的场景。
- 后续工作[10,22,41,45,54,69,92](Implicit functions in feature space for 3d shape re-construction and completion、Neural radiosity、Acorn:Adaptive coordinate networks for neural scene representation、Instant neural graphics primitives with a multiresolution hash encoding、Convolutional occupancy networks、Neural geometric level of detail: Real-time rendering with implicit 3D shapes、Nerf++: Analyzing and improving neural radiance fields)将MLP解码器与低维特征的一级或多级体素网格相结合。这样的混合表示能够更好地表示精细的几何细节并且可以被快速地评估。但是,随着场景大小的增加,它们会导致内存占用量增大。
3D Reconstruction from Multi-view Images
- 经典的多视图立体(MVS)方法[2,6 - 8,35,35,62,64,65]考虑用于深度估计的特征匹配[6,62]或用体素表示形状[2,7,8,35,51,64,72,73]。基于学习的MVS方法通常替代经典MVS流水线的一些部分,特征匹配[23,36,40,74,88]、深度融合[16,57]或从多视图图像推断深度[29,79,80,85]。
- 与经典MVS算法使用的显式场景表示相反,最近的神经方法[39,48,82]通过具有连续输出的单个MLP表示表面。完全从已设定姿势的2D图像学习,它们显示出吸引人的重建结果,并且不受离散化的影响。但是,需要精确的Masked。受NeRF [44]中基于密度的体绘制的启发,其展示了令人印象深刻的无对象掩模的视图合成,一些作品[49,76,81]使用体绘制进行无掩模的神经隐式表面重建。
Incorporating Priors into Neural Scene Representations
- 一些研究人员建议将深度平滑度[46]、语义相似度[30]或稀疏MVS点云[58]等先验知识纳入稀疏输入的新视图合成任务。
- 在本工作中,重点是隐式三维表面重建:
- Manhattan-SDF [21]使用来自COLMAP [63]的密集MVS深度图作为监督,并采用曼哈顿世界先验[11]来处理对应于墙壁、地板等的低纹理平面区域。
- 文章基于数据驱动的单眼深度和法线预测[17]为整个场景提供高质量先验的观察。将这些先验知识结合到神经隐式曲面的优化中,不仅消除了曼哈顿世界假设[11],而且还提高了重建质量,简化了pipeline.
Method
隐式场景表示
我们将场景几何体表示为带符号的距离函数(SDF)。带符号距离函数是一个连续函数f,对于给定的3D点,它返回该点到最近曲面的距离:
f : R 3 → R x → s = S D F ( x ) , ( 1 ) f:R^3 \to R \ \ \ \ x\to s=SDF(x),(1) f:R3→R x→s=SDF(x),(1)
其中,x是3D点,s表示相应的SDF值。在本研究中,我们用可学习参数 θ \theta θ对SDF函数进行参数化,并研究用于表示函数的几种不同设计选择:作为可学习SDF值的密集栅格显式、作为单个MLP隐式或使用MLP与单分辨率或多分辨率要素栅格组合的混合。
- 密集SDF网格:
- 对SDF进行参数化的最直接方法是直接将SDF值存储在离散体积 G θ G_\theta Gθ的每个单元格中,分辨率为 R H × R W × R D [ 31 ] R_H ×R_W ×R_D [31] RH×RW×RD[31]。要从密集SDF格网中查询任意点x的SDF值 s ^ \hat s s^,我们可以使用任何插值运算:
s ^ = i n t e r p ( x , G θ ) , ( 2 ) \hat s=interp(x,G_\theta),(2) s^=interp(x,Gθ),(2) - 在我们的实验中,我们将interp实现为三线性插值。
- 对SDF进行参数化的最直接方法是直接将SDF值存储在离散体积 G θ G_\theta Gθ的每个单元格中,分辨率为 R H × R W × R D [ 31 ] R_H ×R_W ×R_D [31] RH×RW×RD[31]。要从密集SDF格网中查询任意点x的SDF值 s ^ \hat s s^,我们可以使用任何插值运算:
- 单个MLP:
- SDF功能也可通过单个MLP [50]参数化 f θ f_\theta fθ:
s ^ = f θ ( γ ( x ) ) , ( 3 ) \hat s=f_\theta(\gamma(x)),(3) s^=fθ(γ(x)),(3) - 其中, s ^ \hat s s^是预测的SDF值, γ \gamma γ对应于将x映射到更高维空间的固定位置编码[44,70]。在将位置编码函数引入到新颖的视图合成[44]之后,位置4编码函数现在被广泛用于神经隐式表面重建[49,76,81,82],因为它们增加了基于坐标的网络的表达能力[70]。
- SDF功能也可通过单个MLP [50]参数化 f θ f_\theta fθ:
- 带有 MLP 解码器的单分辨率特征网格:
- 我们还可以结合这两种参数化,并使用特征条件 M L P f θ MLP\ f_\theta MLP fθ 和分辨率为 R 3 R^3 R3 的特征网格 Φ θ \Phi_\theta Φθ,其中网格的每个单元存储一个特征向量 [28, 38, 54, 69] 而不是直接存储 SDF价值观:
s ^ = f θ ( γ ( x ) , i n t e r p ( x , Φ θ ) ) , ( 4 ) \hat s=f_\theta(\gamma(x),interp(x,\Phi_\theta)),(4) s^=fθ(γ(x),interp(x,Φθ)),(4) - 注意, M L P f θ MLP\ f_\theta MLP fθ基于来自特征网格 Φ θ \Phi_\theta Φθ的插值局部特征矢量来调节。
- 我们还可以结合这两种参数化,并使用特征条件 M L P f θ MLP\ f_\theta MLP fθ 和分辨率为 R 3 R^3 R3 的特征网格 Φ θ \Phi_\theta Φθ,其中网格的每个单元存储一个特征向量 [28, 38, 54, 69] 而不是直接存储 SDF价值观:
- 带MLP解码器的多分辨率特性网格:
- 代替使用单个特征网格 Φ θ \Phi_\theta Φθ ,人们还可以采用具有分辨率 R l R_l Rl [10、22、45、69、92]的多分辨率特征网格 { Φ θ l } l = 1 L \{\Phi_\theta^l\}_{l=1}^L {Φθl}l=1L。 分辨率在几何空间[45]中采样,以组合不同频率的特征:
R l : = ⌊ R min b l ⌋ b : = exp ( ln R max − ln R min L − 1 ) , ( 5 ) R_{l}:=\left\lfloor R_{\min } b^{l}\right\rfloor \quad b:=\exp \left(\frac{\ln R_{\max }-\ln R_{\min }}{L-1}\right),(5) Rl:=⌊Rminbl⌋b:=exp(L−1lnRmax−lnRmin),(5) - 其中 R m i n 、 R m a x R_{min}、R_{max} Rmin、Rmax分别是最粗分辨率和最佳分辨率。 同样,我们提取每个级别的插值特征并将它们串联在一起:
s ^ = f θ ( γ ( x ) , { i n t e r p ( x , Φ θ l ) } l ) , ( 6 ) \hat s=f_\theta(\gamma(x),\{interp(x,\Phi_\theta^l)\}_l),(6) s^=fθ(γ(x),{interp(x,Φθl)}l),(6) - 随着网格单元的总数呈立方增长,我们使用固定数量的参数来存储特征网格,并使用空间哈希函数在更精细的级别索引特征向量 [45](详见补充资料)。
- 代替使用单个特征网格 Φ θ \Phi_\theta Φθ ,人们还可以采用具有分辨率 R l R_l Rl [10、22、45、69、92]的多分辨率特征网格 { Φ θ l } l = 1 L \{\Phi_\theta^l\}_{l=1}^L {Φθl}l=1L。 分辨率在几何空间[45]中采样,以组合不同频率的特征:
- 颜色预测:
- 除了 3D 几何之外,我们还预测颜色值,以便我们的模型可以通过重建损失进行优化。因此,在 [82] 之后,我们定义了第二个函数 c θ c_\theta cθ
c ^ = c θ ( x , v , n ^ , z ^ ) , ( 7 ) \hat c = c_\theta(x,v,\hat n,\hat z),(7) c^=cθ(x,v,n^,z^),(7) - 预测 3D 点 x 和观察方向 v 的 RGB 颜色值 c ^ \hat c c^。3D 单位法线 n ^ \hat n n^ 是我们的 SDF 函数的分析梯度。特征向量 z ^ \hat z z^ 是 [82] 中 SDF 网络的第二个线性头的输出。我们使用网络权重为 θ \theta θ的双层 MLP 参数化 c θ c_\theta cθ。在密集网格 SDF 参数化的情况下,我们类似地优化密集特征网格并通过插值函数 i n t e r p interp interp 获得特征向量 z ^ \hat z z^。
- 除了 3D 几何之外,我们还预测颜色值,以便我们的模型可以通过重建损失进行优化。因此,在 [82] 之后,我们定义了第二个函数 c θ c_\theta cθ
隐式曲面的体绘制
在最近的工作[49,76,81,82]之后,我们通过使用可微体积渲染的基于图像的重建损失来优化第3.1节中描述的隐式表示。更具体地说,为了渲染像素,我们从摄像机中心投射一个射线r,沿其视线方向穿过该像素。我们沿着射线对M点 x r i = o + t r i v x_r^i=o+t_r^iv xri=o+triv进行采样,并预测它们的 S D F s ^ r i SDF\ \hat s_r^i SDF s^ri和颜色值 c ^ r i \hat c_r^i c^ri。我们按照[81]将 s ^ r i \hat s_r^i s^ri的SDF值转换为用于卷渲染的密度值 σ ^ r i \hat \sigma_r^i σ^ri:
σ β ( s ) = { 1 2 β exp ( s β ) if s ≤ 0 1 β ( 1 − 1 2 exp ( − s β ) ) if s > 0 , ( 8 ) \sigma_{\beta}(s)=\left\{\begin{array}{ll} \frac{1}{2 \beta} \exp \left(\frac{s}{\beta}\right) & \text { if } s \leq 0 \\ \frac{1}{\beta}\left(1-\frac{1}{2} \exp \left(-\frac{s}{\beta}\right)\right) & \text { if } s>0 \end{array}\right.,(8) σβ(s)=⎩⎨⎧2β1exp(βs)β1(1−21exp(−βs)) if s≤0 if s>0,(8)
其中 β \beta β是可学习的参数。根据 NeRF [44],当前光线 r 的颜色 C ^ ( r ) \hat C (r) C^(r) 通过数值积分计算:
C ^ ( r ) = ∑ i = 1 M T r i α r i c ^ r i T r i = ∏ j = 1 i − 1 ( 1 − α r j ) α r i = 1 − exp ( − σ r i δ r i ) , ( 9 ) \hat{C}(\mathbf{r})=\sum_{i=1}^{M} T_{\mathbf{r}}^{i} \alpha_{\mathbf{r}}^{i} \hat{\mathbf{c}}_{\mathbf{r}}^{i} \quad T_{\mathbf{r}}^{i}=\prod_{j=1}^{i-1}\left(1-\alpha_{\mathbf{r}}^{j}\right) \quad \alpha_{\mathbf{r}}^{i}=1-\exp \left(-\sigma_{\mathbf{r}}^{i} \delta_{\mathbf{r}}^{i}\right),(9) C^(r)=i=1∑MTriαric^riTri=j=1∏i−1(1−αrj)αri=1−exp(−σriδri),(9)
其中 T r i T^i_r Tri和 α r i \alpha^i_r αri分别表示沿着射线r的样品点i的透射率和 α \alpha α值,并且 δ r i \delta^i_r δri是相邻样品点之间的距离。 类似地,我们计算与电流射线相交的表面的深度 D ^ ( r ) \hat D(r) D^(r)和法线 N ^ ( r ) \hat N(r) N^(r)为:
D ^ ( r ) = ∑ i = 1 M T r i α r i t r i N ^ ( r ) = ∑ i = 1 M T r i α r i n ^ r i , ( 10 ) \hat{D}(\mathbf{r})=\sum_{i=1}^{M} T_{\mathbf{r}}^{i} \alpha_{\mathbf{r}}^{i} t_{\mathbf{r}}^{i} \quad \hat{N}(\mathbf{r})=\sum_{i=1}^{M} T_{\mathbf{r}}^{i} \alpha_{\mathbf{r}}^{i} \hat{\mathbf{n}}_{\mathbf{r}}^{i},(10) D^(r)=i=1∑MTriαritriN^(r)=i=1∑MTriαrin^ri,(10)
利用单眼几何线索
将体绘制与隐式曲面统一起来会产生令人印象深刻的 3D 重建结果。然而,这种方法很难处理更复杂的场景,尤其是在无纹理和稀疏覆盖区域。为了克服这一限制,我们使用现成的、可高效计算的单眼几何先验,从而改进神经隐式曲面方法。
- 单眼深度提示:
- 一种常见的单眼几何线索是单眼深度图,可以通过现成的单眼深度预测器轻松获得。更具体地说,我们使用预训练的 Omnidata 模型 [17] 来预测每个输入 RGB 图像的深度图 D。注意,一般场景下,绝对尺度是很难估计的,所以必须把D看作是一个相对的cue。然而,这种相对深度信息也在图像中的较大距离上提供。
- 单眼正常线索:
- 我们使用的另一个几何线索是表面法线。与深度线索类似,我们应用相同的预训练 Omnidata 模型来获取每个 RGB 图像的法线图 N。与提供半局部相关信息的深度线索不同,法线线索是局部的并且捕捉几何细节。因此,我们期望表面法线和深度是互补的。
优化
-
Reconstruction Loss:
- 等式 (9) 提供了从 3D 场景表示到 2D 观察的连接。因此,我们可以使用简单的 RGB 重建损失来优化场景表示:
L r g b = ∑ r ∈ R ∥ C ^ ( r ) − C ( r ) ∥ 1 , ( 11 ) \mathcal{L}_{\mathrm{rgb}}=\sum_{\mathbf{r} \in \mathcal{R}}\|\hat{C}(\mathbf{r})-C(\mathbf{r})\|_{1} ,(11) Lrgb=r∈R∑∥C^(r)−C(r)∥1,(11) - 这里 R 表示小批量中的像素/光线集,C® 是观察到的像素颜色。
- 等式 (9) 提供了从 3D 场景表示到 2D 观察的连接。因此,我们可以使用简单的 RGB 重建损失来优化场景表示:
-
Eikonal Loss:
- 按照常见的做法,我们还在采样点上添加了一个Eikonal术语[20],以规范3D空间中的SDF值。
L eikonal = ∑ x ∈ X ( ∥ ∇ f θ ( x ) ∥ 2 − 1 ) 2 , ( 12 ) \\\mathcal{L}_{\text {eikonal }}=\sum_{\mathbf{x} \in \mathcal{X}}\left(\left\|\nabla f_{\theta}(\mathbf{x})\right\|_{2}-1\right)^{2},(12) Leikonal =x∈X∑(∥∇fθ(x)∥2−1)2,(12)
- 按照常见的做法,我们还在采样点上添加了一个Eikonal术语[20],以规范3D空间中的SDF值。
-
Depth Consistency Loss:
- 除了 Lrgb 和 Leikonal,我们还加强了我们渲染的预期深度 ^D 和单眼深度 ¯D 之间的一致性:
L depth = ∑ r ∈ R ∥ ( w D ^ ( r ) + q ) − D ˉ ( r ) ∥ 2 \mathcal{L}_{\text {depth }}=\sum_{\mathbf{r} \in \mathcal{R}}\|(w \hat{D}(\mathbf{r})+q)-\bar{D}(\mathbf{r})\|^{2} Ldepth =r∈R∑∥(wD^(r)+q)−Dˉ(r)∥2 - 其中w和q是用于对齐Dˆ、D的尺度和转移,因为D D只定义为大小。 请注意,这些因素必须每批单独估计,因为不同批次预测的深度图在规模和转移方面可能有所不同。 具体来说,我们解决了w和q,其中有一个最小方形的标准[19,56],它有一个封闭形式的解决方案(详情请参阅补充)。
- 除了 Lrgb 和 Leikonal,我们还加强了我们渲染的预期深度 ^D 和单眼深度 ¯D 之间的一致性:
-
Normal Consistency Loss:
- 类似地,我们对体积渲染的法线 N^ 和预测的单眼法线 N¯ 施加一致性,转换为具有角度和 L1 损失的相同坐标系 [17]:
L normal = ∑ r ∈ R ∥ N ^ ( r ) − N ˉ ( r ) ∥ 1 + ∥ 1 − N ^ ( r ) ⊤ N ˉ ( r ) ∥ 1 , ( 13 ) \mathcal{L}_{\text {normal }}=\sum_{\mathbf{r} \in \mathcal{R}}\|\hat{N}(\mathbf{r})-\bar{N}(\mathbf{r})\|_{1}+\left\|1-\hat{N}(\mathbf{r})^{\top} \bar{N}(\mathbf{r})\right\|_{1},(13) Lnormal =r∈R∑∥N^(r)−Nˉ(r)∥1+∥∥∥1−N^(r)⊤Nˉ(r)∥∥∥1,(13)
- 类似地,我们对体积渲染的法线 N^ 和预测的单眼法线 N¯ 施加一致性,转换为具有角度和 L1 损失的相同坐标系 [17]:
我们用来与外观网络一起优化我们的隐式表面的总损失是:
L = L rgb + λ 1 L eikonal + λ 2 L depth + λ 3 L nermal , ( 14 ) \mathcal{L}=\mathcal{L}_{\text {rgb }}+\lambda_{1} \mathcal{L}_{\text {eikonal }}+\lambda_{2} \mathcal{L}_{\text {depth }}+\lambda_{3} \mathcal{L}_{\text {nermal }},(14) L=Lrgb +λ1Leikonal +λ2Ldepth +λ3Lnermal ,(14)
试验
数据集
虽然以前的神经implicit-based重建方法主要集中在singleobject场景与许多输入视图,在这项工作中,我们调查的重要性单眼几何信号扩展到更复杂的场景。因此我们认为:
- a)实际室内扫描:[67]和复制品ScanNet [13];
- b)真实的大型室内场景:坦克和寺庙[34]高级场景;
- c)对象级场景:[46,84]中稀疏3视图设置中的DTU [1];
Baselines
我们与
- a)最先进的神经隐式表面方法进行比较:UNISURF[49]、VolSDF [81]、NeuS [76]和Manhattan-SDF[21]。
- b)经典的MVS方法:COLMAP [62]和最先进的商业软件(RealityCapture 2)。
- c)具有预测的单目深度线索的TSDF-融合[12],其中GT深度图用于恢复尺度和移位值。
该基线示出了如果仅使用单目深度线索而不使用隐式表面模型的重建质量。
评估指标
对于DTU,我们遵循官方评估协议并报告倒角距离。对于Replica和ScanNet,按照[21,42,53,54,68,92],我们报告了倒角距离、阈值为5cm的F得分以及正态一致性测量。
结果对比
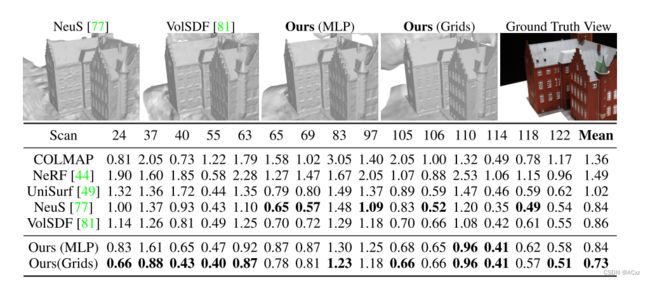
DTU 数据集上的对象级重建将所有输入视图。将 Chamfer 距离与最先进的方法进行了比较。我们使用 MLP 的方法取得了与以前方法相似的结果,而我们使用多分辨率特征网格的方法导致更详细的表面并且大大优于以前的工作。

