信噪比如何计算？如何产生固定信噪比的带噪信号？

一、信号的基础知识

1.1 信号能量的计算

1.1.1 有穷区间能量

    连续时间信号，信号总能量定义为：
$$E(t_1:t_2)={\int }_{t_1}^{t_2}|x(t){|}^{2}dt$$
    离散时间信号，信号总能量定义为：
$$E(n_1:n_2)=\sum _{n=n1}^{n2}|x[n]{|}^2$$

1.1.2 无穷区间能量

    连续时间信号，信号总能量定义为：
$$E_{\infty }\triangleq {\int }_{-\infty }^{\infty }|x(t){|}^2$$
    离散时间信号，信号总能量定义为：
$$E_{\infty }\triangleq \sum _{n=-\infty }^{\infty }|x[n]{|}^2$$

1.2 信号功率的计算

    连续时间信号，信号平均功率定义为：
$$P_{\infty }=\underset{T\to \infty }{\lim }{\int }_{-T}^T|x(t){|}^2$$
    离散时间信号，信号平均功率定义为：
$$P_{\infty }=\underset{N\to \infty }{\lim }\frac{1}{2N+1}|x[n]{|}^2$$

1.3 信号的分类

    根据上述信号能量和信号功率的定义，本章节衍生补充一下信号分类这个知识点～～～

    信号可以分为以下三类：

• 总能量有限$E_{\infty }<\infty$，平均功率为零$P_{\infty }=0$，为能量信号；

• 总能量无限$E_{\infty }=\infty$但平均功率有限$P_{\infty }<\infty$，功率信号；

• 总能量和平均功率都无限，非能非功信号。

    注意：如果信号具有有限的总能量，即$E_{\infty }<\infty$，其平均功率必须为零。

二、信噪比

2.1 信噪比的定义及计算

    信噪比，又叫$SNR$或$S/N$，是指一个电子系统中信号与噪声的比例，信噪比的计量单位通常是$dB$，计算方法是：
$$SNR=10lg\frac{P_s}{P_n}$$

又或是：
$$SNR=20lg\frac{V_s}{V_n}$$

其中$P_s$和$P_n$代表信号和噪声的有效功率，$V_s$和$V_n$是信号和噪声电压的有效值。

2.2 几个仿真小栗子

2.2.1 教你如何生成一个固定的已知功率的高斯白噪声信号

    所谓高斯白噪声，就是幅度分布服从高斯分布，功率谱密度分布服从均匀分布的噪声信号。已知噪声功率，其噪声功率其实就是高斯分布的方差。因此，生成一个固定功率的高斯白噪声信号，只需要使用Matlab的randn命令生成一组正态分布的随机数，并给这组随机数乘以设定功率的平方根即可。代码如下：

%% 仿真验证噪声功率是标准差的平方
clear; clc; close all; warning off;

L = 1000;  % 噪声信号长度
N = 10000;  % 蒙特卡洛试验次数
sigma = 2;  % 噪声标准差
Pn_lis = zeros(1, N);
for i = 1 : N
    noise = sigma * randn(1, L);  % 产生噪声信号
    P_n = sum(noise .^ 2) / length(noise);  % 离散信号平均功率计算公式
    Pn_lis(i) = P_n;
end

% 作图
figure(1); clf;
plot(Pn_lis, 'linewidth', 1.5); hold on;
plot(xlim, [sigma^2, sigma^2], 'm--', 'linewidth', 2); hold off;
legend('仿真的噪声功率曲线', '设置的噪声功率参数'); 
ylim([2, 6]); xlabel('试验次数'); ylabel('噪声功率'); set(gca, 'fontsize', 14);
title(['标准差=', num2str(sigma), '    噪声功率的平均值=', num2str(mean(Pn_lis))]);

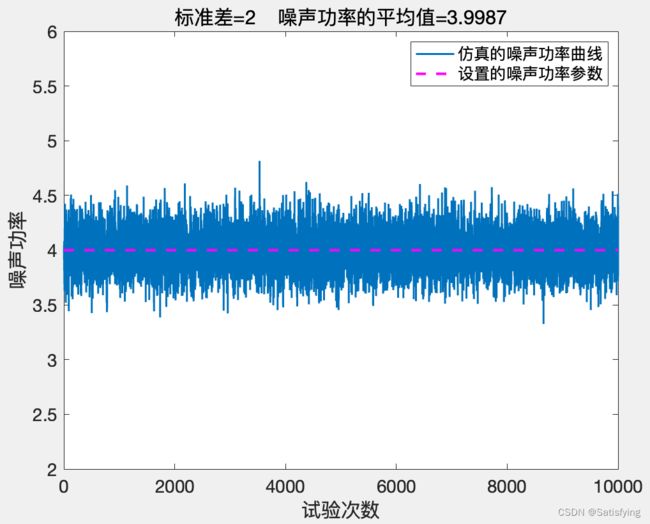
运行结果：

    上面仿真图中，粉色虚线是事先设置好的噪声功率值，蓝色曲线是10000次蒙特卡洛实验每一次的噪声功率值分布曲线。从仿真结果看，仿真设置的噪声的标准差为2，进行10000次蒙特卡洛实验得到的噪声功率的平均值为3.9988，$3.9988\approx 2^2$ 。因此可以得到结论：使用Matlab的randn函数生成随机数并乘以噪声功率的平方根$\sqrt{P_n}$，确实可以生成功率为$P_n$ 的高斯白噪声。

2.2.2 教你如何计算信噪比

   计算信噪比只需要带入上述信噪比公式，下面将用功率比的方式来举例，进行仿真计算。

%% 计算信噪比仿真
clear; clc; close all; warning off;

% 参数设置
T = 2;  % 仿真时长
fs = 1000;  % 采样频率
t = 0 : 1/fs : T;
L = length(t);  
A = 10;  % 幅值
fc = 10;  % 载频
P_n = 2;  % 噪声功率

% 产生仿真信号
signal = A * cos(2 * pi * fc .* t);  % 生成有效信号
noise = sqrt(P_n) .* randn(1, L);  % 产生高斯白噪声信号

% 计算信噪比
P_s = sum(signal .^ 2) / L;  % 信号功率
P_n = sum(noise .^ 2) / L;  % 噪声功率
SNR = 10 * log10(P_s / P_n);  % 信噪比
fprintf('\t信号的平均功率为：%.2fW\n', P_s);
fprintf('\t噪声的平均功率为：%.2fW\n', P_n);
fprintf('\t信噪比为：%.2fdB\n', SNR);

figure(1); clf;
subplot(2, 1, 1);
plot(t, signal, 'b', 'linewidth', 2); hold on;
plot(t, noise, 'k', 'linewidth', 1); hold on;
plot(t, signal+noise, 'g', 'linewidth', 1);
xlabel('t'); ylabel('y'); axis('tight'); title('全部信号波形'); set(gca, 'fontsize', 14);
subplot(2, 1, 2);
plot(t(100:500), signal(100:500), 'b', 'linewidth', 2); hold on;
plot(t(100:500), noise(100:500), 'k', 'linewidth', 1); hold on;
plot(t(100:500), signal(100:500)+noise(100:500), 'g', 'linewidth', 1);
legend(['信号功率≈', num2str(P_s, '%.2f'), 'W'], ['噪声功率≈', num2str(P_n, '%.2f'), 'W'], ...
    ['信噪比≈', num2str(SNR, '%.2f'), 'dB'], 'location', 'eastoutside');
xlabel('t'); ylabel('y'); axis('tight'); title('放大局部观察信号细节'); set(gca, 'fontsize', 14);
set(gcf, 'position', [12, 60, 1450, 650]);

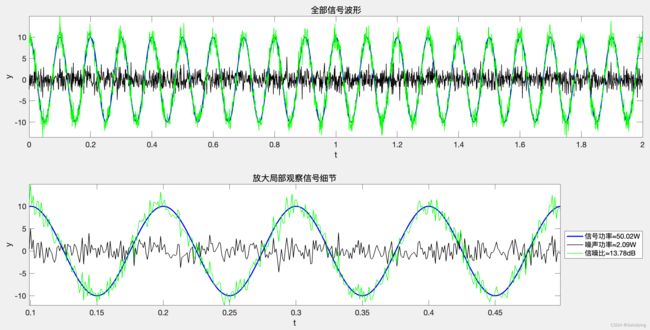
运行结果：

2.2.3 教你如何生成一个固定信噪比的带噪信号

   根据上述信噪比的计算公式可知，信噪比的计算只和两个变量有关系，即信号功率$P_s$和噪声功率$P_n$，因此，任意已知信号功率$P_s$、噪声功率$P_n$和信噪比$SNR$的其中两项，可以求得另外一项。利用这一特性，可以生成固定信噪比的带噪信号。

   基本思路是：

• 第一步，根据已知的有效信号计算出信号功率；
• 第二步，根据设定的信噪比参数计算出噪声功率；
• 第三步，根据计算到的噪声功率可以得到噪声的数字信号表达式；
• 最后一步，将有效信号和噪声信号表达式相加即得到设定信噪比条件下的带噪信号。

   用数学公式表示为：
$$SNR=10lg\frac{P_s}{P_n}⟹P_n=\frac{P_s}{10^{SNR/10}}$$

   仿真代码如下：

%% 产生固定信噪比的带噪信号
clear; clc; close all; warning off;

% 参数设置
T = 2;  % 仿真时长
fs = 1000;  % 采样频率
t = 0 : 1/fs : T;
L = length(t);  
A = 10;  % 幅值
fc = 10;  % 载频
SNR = 5;  % 设定信噪比参数

% 生成有效信号
signal = A * cos(2 * pi * fc .* t);  % 生成有效信号
P_s = sum(signal .^ 2) / L;  % 信号功率

% 产生带噪信号
P_n = P_s / (10 ^ (SNR / 10)); 
noise = sqrt(P_n) .* randn(1, L);  % 噪声信号
s_noise = signal + noise;

% 验证生成的带噪信号的信噪比是否等于设定参数
P_n_real = sum(noise .^ 2) / L;
SNR_real = 10 * log10(P_s / P_n_real);
fprintf('\t设定的信噪比参数为：%.2fdB\n', SNR);
fprintf('\t实际的带噪信号的信噪比为：%.2fdB\n', SNR_real);

figure(1); clf;
subplot(2, 1, 1);
plot(t, signal, 'b', 'linewidth', 2); hold on;
plot(t, noise, 'k', 'linewidth', 1); hold on;
plot(t, s_noise, 'g', 'linewidth', 1);
xlabel('t'); ylabel('y'); axis('tight'); title('全部信号波形'); set(gca, 'fontsize', 14);
subplot(2, 1, 2);
plot(t(100:500), signal(100:500), 'b', 'linewidth', 2); hold on;
plot(t(100:500), noise(100:500), 'k', 'linewidth', 1); hold on;
plot(t(100:500), s_noise(100:500), 'g', 'linewidth', 1);
legend(['信号功率≈', num2str(P_s, '%.2f'), 'W'], ['噪声功率≈', num2str(P_n_real, '%.2f'), 'W'], ...
    ['信噪比≈', num2str(SNR_real, '%.2f'), 'dB'], 'location', 'eastoutside');
xlabel('t'); ylabel('y'); axis('tight'); title('放大局部观察信号细节'); set(gca, 'fontsize', 14);
set(gcf, 'position', [12, 60, 1450, 650]);

运行结果：

 
 
（本文完整的pdf请关注下方，并回复 “010” 获取~）