卷积神经网络 (为什么是卷积?)
卷积神经网络(Conventional Neural Network, CNN)是深度学习的重要算法之一,常常应用在计算机视觉问题中,如图像分类(Image classification)和目标检测(Object detection)等。
在学习了传统全连接神经网络之后,直接使用传统网络来进行图片处理会出现参数爆炸的问题。试想一下用全连接神经网络处理一个 1000 x 1000 像素的 RGB 三通道图片,其输入层有 1000 x 1000 x 3 = 3 百万个节点,即使只设置节点为 128 的隐藏层,需要训练的参数就达到了 3 百万 x 128 = 3 亿。这才仅仅是一层隐藏层需要的参数个数。而现实问题的复杂程度不可能用 1 层隐藏层就解决问题,也就是说一个正常的网络需要训练的参数会达到一个天文数字。更可怕的是 如此多的参数极有可能会造成过拟合问题发生。此外,传统的全连接神经网络仅仅将像素点依次排开进行输入,则 会导致图片中的某些“结构信息”丢失,如上下左右像素点之间的特征。
探究人脑识图的过程
科研人员在研究人的大脑发现,当我们在看到一个事物并尝试识别它时,往往会经历下述 3 个阶段。以人脸识别为例,首先,大脑会识别读入的图片的边缘(各种轮廓);然后,大脑继续将这些边缘整合成事物的某些组件(鼻子,耳朵等);最后,大脑将这些小部分整合成最后的对象(人脸)。

因此,卷积神经网络也是模仿人类识别图像的过程,即不是一步到位识别出图像中的人脸,而是一步步由简到难识别出人脸来的。
边缘检测 Edge Detection
介绍边缘检测之前,先说一下卷积网络中的 点乘 操作。对于一个 6x6 的输入图片,我们设定一个 3x3 的filter 矩阵(有时也成为 卷积核 或 滤波器 ),我们以 1 为步长,依次选取图片中的 3x3 矩阵与 filter 矩阵相点乘,最终可以得到一个 4x4 的输出矩阵,如下展示了点乘的操作步骤,
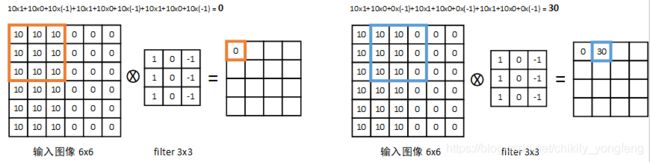
由于矩阵中的数值代表着一定颜色深度的因此输入图像可以看做是一个垂直的边缘。在经历了上述点乘操作后,我们发现这个 3x3 的 filter 是可以检测出输入图像的边缘特征的(即明和暗)。
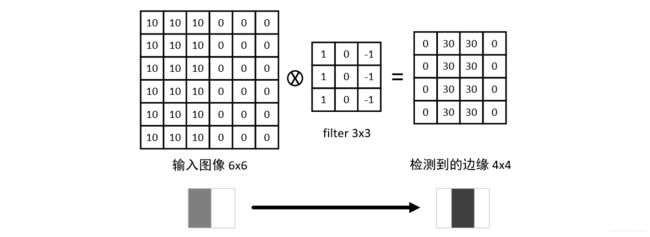
依次类推,我们可以将上述的 filter 翻转 90 度,这样一来新的 filter 就可以检测出水平的边缘了。事实上,在过去的研究过程中,研究人员提供了几种固定的 filter 矩阵,如 Sobel filter 和 Scharr filter,我们可以直接套用这些 filter,当然也可以将矩阵中的数值作为参数,并通过深度学习的反向传播算法来获得 filter 中的这些参数,这样的 filter 能更高效的找到图像中的边缘。

填充 Padding
卷积网络中除了点乘之外,还有另一个很重要的操作,即 填充。顾名思义,填充的作用就是将原输入矩阵的外围填充上一层或几层的 0 ,填充输入矩阵之后再与 filter 做点乘操作。假设我们不进行填充操作,则会出现下列情况:1. 输入图片通过层层 filter 不断缩小,最后只有一点点;2. 输入图片的边缘信息可能会丢失。为此,即使填 0 会阻止上述情况发生。
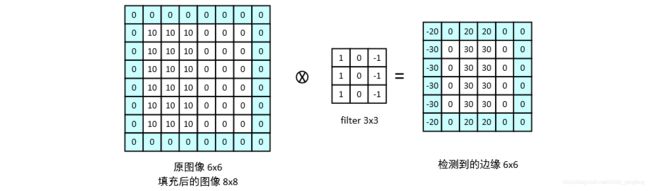
由图可见,填充前图像左上角的 10 影响到的输出只有 1 个,而填充后图像左上角的 10 影响到的输出有 4 个了。在卷积神经网络中有 2 种形式的卷积类型,一种是 Valid convolution,该操作不使用填充操作;另一种是 Same convolution,该操作使用填充操作,且保证输入输出的矩阵大小相同。
这里我们记 原图像大小为 n × n n\times n n×n,滤波器 filter 的大小为 f × f f \times f f×f,填充的层数为 p p p,如果使用 Same convolution,则必须满足等式 n + 2 × p − f + 1 = n n + 2\times p - f + 1 = n n+2×p−f+1=n 成立,即要求 p = f − 1 2 p = \frac{f-1}{2} p=2f−1。这也间接说明了为什么通常设置的 filter 的大小都是奇数相乘(如 3x3,5x5,或 7x7)而不是偶数相乘。
跨步卷积 Strided Convolution
之前的卷积操作都是跨一步进行的,也就是说输入矩阵每次与 filter 点乘都是左移或下移 1 个单位。事实上也存在每次跨两个单位行点乘,卷积网络定义这个 1 或 2 个单位为步长。
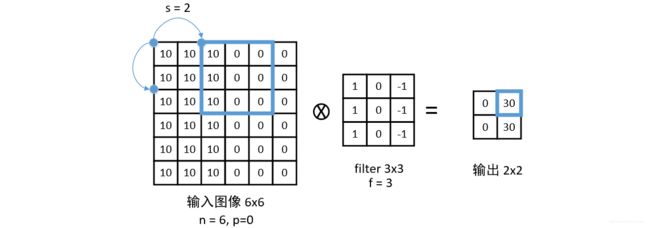
我们定义步长 s s s,则进行填充和卷积后的输出维度为,
输 出 维 度 = ⌊ n + 2 × p − f s + 1 ⌋ 输出维度 = \lfloor \frac{n+2\times p-f}{s} + 1 \rfloor 输出维度=⌊sn+2×p−f+1⌋
三维卷积 3D Convolution
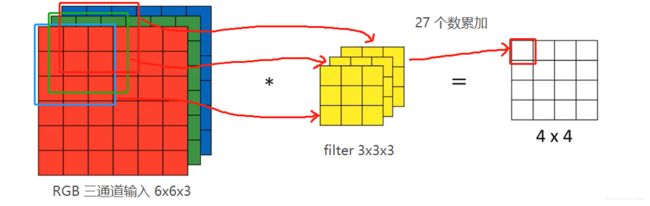
我们日常的图片是彩色的,也即 RGB 三种通道。此时的输入不再是单个 6x6 矩阵了,而是 3 个 6x6 矩阵了,这就构成了一个输入立方体。对于三维输入的卷积,采用如下规则进行。
首先,原输入通道数为 3,则 filter 也必须有 3 个通道(即 3x3x3)。其次,输出矩阵每个单元的结果为输入每个通道的矩阵 与 filter 的对应通道的矩阵 点乘的累加,即 27 个数之和。
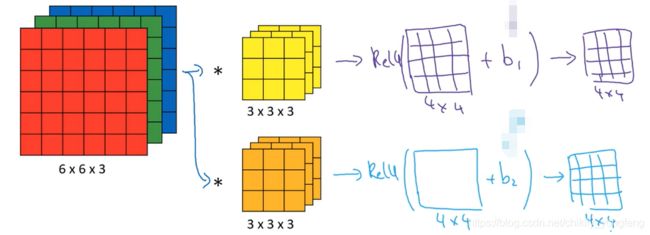
此外,卷积网络允许使用多个 3x3x3 的 filter,想象一下每个 filter 都是在检测不同方向的边缘(垂直的、水平的或倾斜的)。此时 filter 的个数 与 输出矩阵的个数 相同。如下图所示,当设置 2 个 filter 的时候,此时输出就是 2 个 4x4 的矩阵,这 2 个矩阵构成了输出矩阵,大小为 4x4x2。
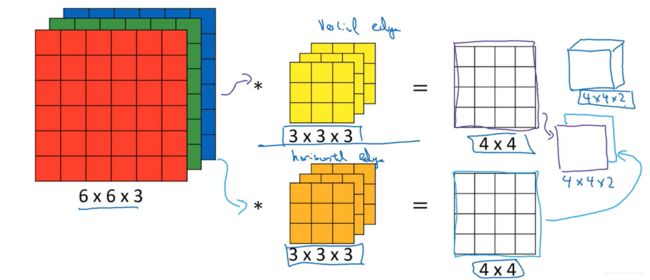
记输入图片的大小为 n × n × n c n\times n \times n_{c} n×n×nc,其中 n c n_c nc 为图片的通道数( n c = 3 n_c=3 nc=3),则滤波器 filter 的大小应该为 f × f × n c f\times f\times n_c f×f×nc。假设 filter 有 n f n_f nf 个( n f = 2 n_f=2 nf=2),则最终的输出大小应该为 ( n − f + 1 ) × ( n − f + 1 ) × n f (n-f+1) \times(n-f+1)\times n_f (n−f+1)×(n−f+1)×nf。 由此可知,最终输出的深度与滤波器 filter 的个数是一致的。
激活函数 Activation
在卷积操作后的结果其实往往并不是下一层网络的输入,我们需要在上述的输出结果上添加偏置项 b 1 , b 2 b_{1}, b_{2} b1,b2 并套用激活函数,如下图所示。这就是一个非常简单的卷积网络层了,所有复杂的卷积网络层都是由这样的基本网络构成的。
池化 Pooling
卷积神经网络通常使用 池化层 来缩减模型大小,提升运算速度。一般来讲,池化操作跟卷及操作类似也会有 f f f 和 s s s 两个超参数, f f f 代表操作区域的大小, s s s 表示步长,下图以 f = 2 , s = 2 f=2,s=2 f=2,s=2 为例展示了 Max Pooling 和 Mean Pooling 的基本操作。换句话说,前者求区域内的最大值,后者求区域内的平均值。
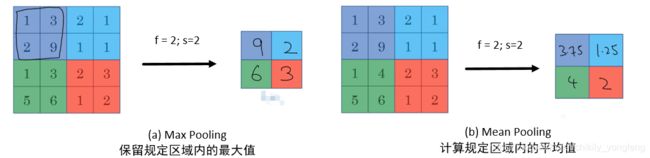
注意,池化层在网络的反向传播算法时并没有要调整的参数,因为 f f f 和 s s s 都是事先规定好的超参数。从另一个角度看,池化层是卷积网络中的静态层。
卷积神经网络示例 CNN Examples
根据之前研究人员设计的卷积神经网络来看,大家倾向于在一个或多个卷积层(Conv)后连接一个池化(Pool)层,这一个组合我们合称之为一层(Layer)。这类型的网络层可以重复很多次,最终连接一个或多个全连接层,输出最终的结果。如果是二分类,则最后接逻辑回归;如果是多分类,则最后接 Softmax 回归。下面给出两个典型的卷积神经网络结构,即 LeNet-5 和 AlexNet。
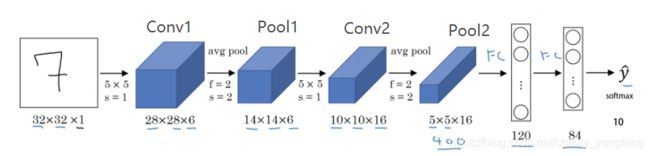
LeNet-5: 在 LeNet-5 中,输入是只有 1 个通道的,即 32x32x1 中的 “1” 的含义。后接 6 个 5x5 的 filter,因此第一层卷积层 Conv1 的输出大小为 (32-5+1)x(32-5+1)x6 = 28x28x6。第一层池化层 Pool1 使用的是 Mean Pooling,其输出大小为 ((28-2)/2+1)x((28-2)/2+1)x6 = 14x14x6。
第二层卷积层 Conv2 包含了 16 个 5x5 的filter,因此 Conv2 的输出大小为 (14-5+1)x(14-5+1)x16 = 10x10x16, 第二层池化层 Pool2 同样使用的是 Mean Pooling,其结果是 ((10-2)/2+1)x((10-2)/2+1)x16 = 5x5x16。最终,这 400 (=5x5x16)个神经元平铺起来,后面连接 120 和 84 的全连接神经网络。最终的输出利用 Softmax 回归输出预测概率。LeNet-5 总计有约 6 万个参数,且使用 ReLU 作为激活函数。,
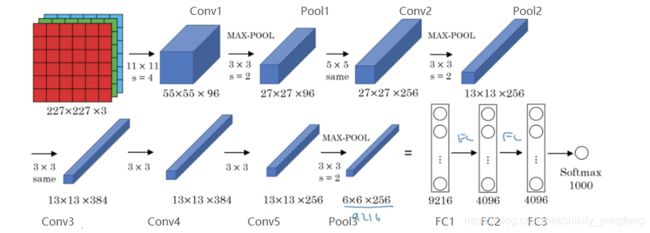
AlexNet: 在 AlexNet 中输入通道是 3 个,前 2 个组合是“卷积层+池化层”。值得注意的是从第 3 层卷积层起,AlexNet 使用 Same convolution。换句话说,第 3,4,5 层卷积层都进行了填充操作(Padding)来确保前后层网络的大小都是 13x13x n f n_f nf。最后 AlexNet 进行了 3 层全连接层外加 Softmax 回归输出最终的预测概率。AlexNet 总计约有 6 千万个参数,使用 ReLU 作为激活函数。
为什么是卷积?
为什么研究人员倾向于使用卷积来处理图像问题?一个很主要的原因(文章开头提到的参数爆炸的问题和丢失结构信息的问题)就是因为全连接神经网络的参数太多了,一旦输入维度增加,训练模型会十分耗计算量。相反,在卷积神经网络中,你会发现无论你的输入图像是多少维,你所需要训练的参数基本上与卷积层中使用的 filter 中的参数相关。当然,卷积网络的参数大部分还是后面的全连接层的参数,卷积层的参数占比很少。这当然会很大程度减少训练的参数,从而减少计算量。
另外,在卷积层中,同一个 filter 可以检测出图像中不同位置的边缘。这样做的好处是:当图像中的边缘进行平移或翻转时,我们用一个 filter 就可以检测出来,从而避免每个位置的都设置一个 filter 来检测边缘。卷及网络的这个特性我们称之为 “参数共享”,即 Parameter Sharing。最后,在卷积层中,输出矩阵的每一个单元值都只与输出矩阵的某块区域(而非全部区域)相关。如 3x3 的 filter 情况下,输出单个值只与输入矩阵的 3x3 的子区域相关,而与其他区域的不相关。这样做的好处是一方面减少了参数的个数,同时也防止模型过拟合。卷积网络的这个特性,我们称之为 “稀疏连接”,即 Sparsity of Connections。总的来讲,这 2 个特性也是造成今天卷积神经网络在图像处理领域举足轻重的主要原因。