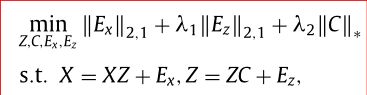多视图聚类方向：子空间学习

策略：首先基于多个视图生成一致性表示，再应用现有的聚类算法，如谱聚类来实现最终的聚类结果。

子空间学习（subspace learning):假设视图间有一个潜在子空间，学习目的是从视图中获得一个合适的子空间，然后为所有视图生成一致性表示，然后将共同的子空间表示矩阵利用谱聚类得到最后的聚类结果。

例如：

• Gao hongchang等人首先学习得到多个视图数据的公共子空间表示，再用谱聚类方法对子空间表示矩阵进行聚类得到最后的聚类结果。[16]
• Liu Iialu等人首先利用非负矩阵分解对多个视图信息进行融合，得到集成多个视图信息的系数矩阵，再用K均值方式得到最后的聚类结果。[25]
• Yuhong等人利用低秩表示融合多个视图信息获得一致性低秩矩阵，再将其一致性矩阵利用主动三支谱聚类得到最后的聚类结果。[34]
• K等人利用典型相关分析（Canonical correlation analysis，CCA）将多视图的高维数据投影到低维子空间中，再进行选标准聚类方法进行聚类。[37]

基于非负矩阵分解的多视图聚类方法[28-30]

由于多视图数据常常具有高维的数据特点，非负矩阵分解(Non-negative MatrixFactorization，NMF)在数据降维上具有优良的性能。基于NMF的多视图聚类方法由于其简单性和可解释性而已成为广泛使用的多视图聚类算法。

• Liu Jialu等[25]首次将非负矩阵分解应用于多视图聚类中，结合基与中心的共正则化策略融合视图间的信息，提出的MultiNMF方法取得了较好的聚类结果。
• Zong Xianchao等[26]将局部结构约束与NMF结合用于多核视图聚类,在聚类的同时保持数据的局部结构。
• Wang Xiumei 等[27]利用成对约束和NMF用于多视图聚类，同时考虑视图内的相似性和视图间的相似性，获得视图的一致性信息。
• Cheng Wei等[48]利用semi-NMF用于多视图聚类。
• 2014年 Li Shaoyuan等[49]提出的PVC方法首次利用NMF和L1稀疏规则算子对两个存在缺失数据的视图进行聚类，PVC的主要思想是在不同视图中描述同一样本的实例应该彼此相似，在视图内部相似的实例应该被划分到同一类。该方法在处理部分视图聚类表现更好，使得基于NMF的多视图聚类方法更多的被用于处理不完整多视图数据。例如 Shao Weishang 等[50]提出的MIC方法结合weighted-NMF和 L2,1规则化对不完整多视图数据进行聚类。Hu Meng等[51]对MIC进行扩展通过weighted semi-NMF和L2,1规则化，使之能处理属性值为负的样本。G.Rai等[52提出的GPMVC方法利用NMF和对每个视图添加图约束使得能处理多个不完整多视图聚类。Zhao Handong 等[53提出的IMG方法结合PVC 和流形学习去捕捉所有样本的全局结构。Qian Bin 等[54提出的DCNMF方法利用簇间相似性和图约束两层约束进行部分多视图聚类。Zhang Xianchao 等[55]和Zong Linlin 等l56利用半监督学习方法结合非负矩阵分解解决视图间的样本对应关系是完全未知的问题，通过在少量视图间样本的对应关系已知的情况下，并提供一种视图间样本关系传递的方式，来得到尽可能多视图间样本的匹配信息，已获得更好的聚类结果。
   

---

adaptive weighted graph fusion incomplete multi-view subspace clustering 2020 

 本文方法：首先，为了消除噪声，我们将全部的原始数据转换成潜在表示（可以为每个视图贡献出更好的graph construction），然后我们合并特征提取和不完整的图融合入一个统一的框架，同时两个过程可以相互协商，共同为一个图学习任务服务。一个稀疏正则化被强加在完整图上为了使其具有鲁棒性关于视图不一致。除此之外，不同视图的重要性被自动学习，大大指导了完整视图的构建。

现有的多视图聚类方法：多核聚类；协同训练和协同正则化；第三种策略协作地转换多视图信息为紧密的共同二进制代码空间，然后在hamming空间进行聚类处理并且使用超越算法加速；最后一种基于子空间的聚类算法，它假设高维数据点是从各种低维子空间描绘得到的，并且每一个簇也能从一个子空间中得到，主要思想是找到几个嵌入在潜在空间中的低维表示然后为下游聚类任务获得一个联合的表示，除此之外，目标是通过矩阵分解/非负矩阵分解找到一个共享的低维潜在表示。

不完整多视图聚类方法：基于非负矩阵分解的方法和基于图的。基于NMF的方法旨在直接获得一个共同的低维表示通过非负矩阵分解。

半非负矩阵分解：

本文想法： 

---

Feature concatenation multi-view subspace clustering

FCMSC

 为了利用互补信息，加入图正则化约束，可以保留局部流形结构，gr-FCMSC:

数据集：

BBCSport （2个视图，每个视图有5个class,总共544条数据） 

Movies617(2个视图，每个视图有17个class，总共617条数据）

MSRCV1(5个视图，每个视图有7个class,总共210条数据）

Olympics(9个视图，每个视图有28个class，总共464条数据）

ORL（3个视图，每个视图有40个class,总共400条数据）

Yale Face(3个视图，每个视图有15个class，总共165条数据）

---

2.子空间聚类聚类问题

①代数方法

        包括基于矩阵分解的方法和代数几何的方法。基于矩阵分解的方法通过对数据矩阵的低秩分解获得点的划分，因此可以看作PCA从单个到多个独立线性子空间的拓展。但该方法需要预先知道矩阵的秩且要求各子空间相互独立。
       广义主成分分析 (GPCA)是代数方法中的一个代数几何方法，与基于矩阵分解的方法不同的是GPCA不要求线性子空间独立，因此既能处理子空间相互独立的情形也能处理子空间不独立的图形。GPCA用一组 多项式对高维数据进行拟合，多项式在某一数据点的梯度给出了包含该点的子空间的法向量。因此当子空间的个数和维度较小时，算法的计算复杂度也低，但随着子空间个数和维度的增加算法的计算复杂度将呈指数增长。当数据无噪声时，GPCA不用预先知道子空间的个数和维度。另外，由于计算多项式系数向量时采用最小二乘法，因此算法对异常值敏感。

②迭代方法
迭代式方法可以看作是对代数式方法的一种提升。首先通过对数据集的随机分割获得类簇的初始划分，然后对各簇数据集用PCA拟合一个子空间，接着将每个数据点划分到距离它最近的子空间，最后不断重复后两步直到满足收敛条件。K平面算法和K子空间算法是两个经典的迭代方法，两者思路类似K均值(K-Means) 算法，但数据的空间分布存在不同，前者的数据来自超平面，后者则来自仿射子空间。该类算法的优点主要体现在算法的简单上，且能保证迭代在有限步内收敛到一个局部最优解。同时类似于K-Means算法，迭代方法的也将对初始化结果敏感。另外，显然该方法需要预先给定子空间的个数和维度。

③统计方法

代数方法和迭代方法只利用了联合子空间的代数和几何性质，并未对子空间内的数据和噪声的分布做出假设，因此所得的结果并非最优。为解决该问题，统计方法为子空间内的数据定义了生成模型。譬如混合概率主成分分析(MPPCA)通过使用混合的概率PCA模型将概率PCA模型 (PPCA)拓展到了联合子空间。然后通过期望最大化(EM)算法获得混合模型参数的极大似然估计。类似于软K均值算法与K均值算法(也称为硬K均值)之间的关系，MPPCA可以看作K子空间算法在数据点的再分配中采用软分配替代硬分配。但MPPCA预先获知子空间的个数和维度。
        随机抽样一致性算法 (RANSAC)通过迭代法从一组有离群点的数据样本点中拟合统计模型。假设子空间的维度均为d,那么RANSAC每次拟合的模型就是一个维度为d的子空间。RANSAC算法有如下优点:有明确的步骤处理离群点:不需要假设子空间独立，也不需要知道子空间的个数,但实际上子空间的个数间接决定于用户定义的阈值。RANSAC也有严重的缺点，比如上述算法描述中假设每个子空间的维度相同，当子空间的维度各不相同时，则需要通过遍历的方式进行。

④基于谱聚类

基于谱聚类的方法是高维数据聚类分析的重要方法之一-。该类算法主要分两步:第一步也是最为重要的一步，构建数据点间的相似度矩阵。第二步，对所得相似度矩阵使用谱聚类。该类方法最大困难点在于如何定义一个好的相似度矩阵。因为两个数据点可能距离很近却位于不同的子空间，或者两个点距离很远却位于相同的子空间，所以使用基于距离度量的相似度矩阵并不合理。按照相似度矩阵的计算方式，基于谱聚类的方法又可以大致分为三类:基于分解的方法、基于高阶模型的方法、基于自表示的方法。
       基于自表示的方法的基本思想是将样本点表示为同一子空间内其它点的线性组合，然后利用组合系数矩阵构建相似度矩阵。不同于其它基于临近点的线性表示方法，例如局部子空间邻接算法 (LSA)、谱局部最佳拟合平面 (SLBF)、局部线性流型聚类(LLMC)等，后者往往根据点对之间的角距离或者欧式距离确定表示字典，而基于自表示的方法将整个数据集视为表示字典，然后将每个点表示成其它数据点的线性组合。为了解决数据的自表示模型所产生的不适定问题，Elhamifar 和Vidal在文献中引入了稀疏性准则，提出了SSC算法。该算法将每个点写成所有其它点的稀疏线性组合, 然后最小化非零表示系数的个数。文献中 表明如果各子空间独立或不相交，每个点可以表示为同一子空间中其它点的稀疏线性组合。文献中 Liu等人对自表示系数矩阵引入了低秩约束提出了LRR算法。LRR算法在低秩性约束下共同地获得了所有数据点的子空间表示，因此能更好地获得数据的全局结构关系。但是相比SSC算法，LRR算法所获得的系数矩阵往往是稠密的，不利于谱图算法的类簇划分。
       在自表示模型和稀疏低秩约束的基础上，研究人员还提出了许多改进的算法。在文献中，Lu等人在子空间划分问题中引入最小二乘回归(LSR)模型，所提算法不仅对有界扰动具有鲁棒性，而且由于算法具有闭式解大大提高了算法的运行效率。在文献中，Wang等人认为系数表示矩阵一般同时具有稀疏性和低秩性，提出了低秩稀疏子空间聚类算法(LRSSC)， 并且给出了算法有效的理论保证。实验结果表明LRSSC算法能既能保留自表示特性，又能拥有图连通性。针对数据不充分或严重受噪声污损情况，提出隐低秩表示算法(LatLRR)。该算法同时使用观测数据和隐式数据构建表示字典，并将子空间分割和特征提取过程融合到同一的框架之中。Lu 等人认为稀疏性和整体效应(grouping effect)对子空间分割都十分重要，前者保证所得系数表示矩阵的块对角特性，后者保证同一空间中的数据点能被正确分组，因此通过引入trace Lasso约束，提出了关系自适应子空间分割算法(CASS)。（2018）