主成分分析（PCA）原理与故障诊断（SPE、T^2以及结合二者的综合指标）-MATLAB实现

转载请注明作者和出处：http://blog.csdn.net/u013829973
系统版本：window 7 （64bit）
MATLAB版本：MATLAB2016b

1.PCA原理

2.求解方法

3.pca故障诊断

4.MATLAB程序实现

1.构造数据

 其中 $num\_sample = 100,a = 10*randn(num\_sample,1)$

2.定义故障

在测试集$x_2$的第51-100行加入幅值为15的阶跃故障

3.混合指标

用一个结合$SPE$ 和$T^2$的混合指标监控故障

\begin{array}{l}
\varphi = \frac{{SPE({\bf{x}})}}{{{\delta ^2}}} + \frac{{{T^2}({\bf{x}})}}{{\chi l^2}} = {{\bf{x}}^T}\phi {\bf{x}}\
\phi = \frac{{{\bf{P}}{{\bf{v}}^{ - 1}}{\bf{P}}{}^T}}{{\chi l^2}} + \frac{{{\bf{I}} - {\bf{PP}}{}^T}}{{\delta _{}^2}}
\end{array}
其中： $\phi $ 是对称且正定的。

4.主元个数确定

$CPV=\frac{\sum _{i=1}^L{\lambda }_i}{\sum _{i=1}^n{\lambda }_i}$ ，$L$ 为主元个数，一般$CPV=85\%$ 。

5.MATLAB代码

close all;
clear all;
clc;
%% 产生训练数据
num_sample=100;
a=10*randn(num_sample,1);
x1=a+randn(num_sample,1);
x2=1*sin(a)+randn(num_sample,1);
x3=5*cos(5*a)+randn(num_sample,1);
x4=0.8*x2+0.1*x3+randn(num_sample,1);
x=[x1,x2,x3,x4];
xx_train=x;
%% 产生测试数据
a=10*randn(num_sample,1);
x1=a+randn(num_sample,1);
x2=1*sin(a)+randn(num_sample,1);
x3=5*cos(5*a)+randn(num_sample,1);
x4=0.8*x2+0.1*x3+randn(num_sample,1);
xx_test=[x1,x2,x3,x4];
xx_test(51:100,2)=xx_test(51:100,2)+15*ones(50,1);

Xtrain =xx_train;
Xtest =xx_test;
%标准化处理：
X_mean = mean(Xtrain);  %按列求Xtrain平均值                           
X_std = std(Xtrain);    %求标准差                      
[X_row,X_col] = size(Xtrain); %求Xtrain行、列数               
                                          
Xtrain=(Xtrain-repmat(X_mean,X_row,1))./repmat(X_std,X_row,1);

%求协方差矩阵
sigmaXtrain = cov(Xtrain);
%对协方差矩阵进行特征分解，lamda为特征值构成的对角阵，T的列为单位特征向量，且与lamda中的特征值一一对应：
[T,lamda] = eig(sigmaXtrain);                            
% disp('特征根（由小到大）');
% disp(lamda);
% disp('特征向量：');
% disp(T);                                            

%取对角元素(结果为一列向量)，即lamda值，并上下反转使其从大到小排列，主元个数初值为1，若累计贡献率小于90%则增加主元个数
D = flipud(diag(lamda));                            
num_pc = 1;                                         
while sum(D(1:num_pc))/sum(D) < 0.9   
num_pc = num_pc +1;
end                                                 

%取与lamda相对应的特征向量
P = T(:,X_col-num_pc+1:X_col);                            
TT=Xtrain*T;
TT1=Xtrain*P;
%求置信度为99%、95%时的T2统计控制限                       
T2UCL1=num_pc*(X_row-1)*(X_row+1)*finv(0.95,num_pc,X_row - num_pc)/(X_row*(X_row - num_pc));


%置信度为95%的Q统计控制限
for i = 1:3
    theta(i) = sum((D(num_pc+1:X_col)).^i);
end
h0 = 1 - 2*theta(1)*theta(3)/(3*theta(2)^2);
ca = norminv(0.95,0,1);
QUCL = theta(1)*(h0*ca*sqrt(2*theta(2))/theta(1) + 1 + theta(2)*h0*(h0 - 1)/theta(1)^2)^(1/h0);                           

%在线监测：
%标准化处理
n = size(Xtest,1);
Xtest=(Xtest-repmat(X_mean,n,1))./repmat(X_std,n,1);

%求T2统计量，Q统计量
[r,y] = size(P*P');
I = eye(r,y);

T2 = zeros(n,1);
Q = zeros(n,1);
for i = 1:n
    T2(i)=Xtest(i,:)*P*pinv(lamda(X_col-num_pc+1:X_col,X_col-num_pc+1:X_col))*P'*Xtest(i,:)';  
    Q(i) = Xtest(i,:)*(I - P*P')*(I - P*P')'*Xtest(i,:)';                                                                                    
end

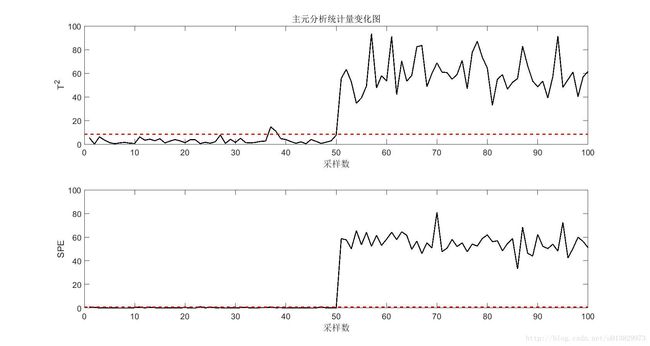
%绘图
    figure
    subplot(2,1,1);
    plot(1:n,T2,'k');                                    
    title('主元分析统计量变化图');
    xlabel('采样数');
    ylabel('T^2');
    hold on;
    line([0,n],[T2UCL1,T2UCL1],'LineStyle','--','Color','r');
    
    subplot(2,1,2);
    plot(1:n,Q,'k');
    xlabel('采样数');
    ylabel('SPE');
    hold on;
    line([0,n],[QUCL,QUCL],'LineStyle','--','Color','r');
    
%贡献图
%1.确定造成失控状态的得分
S = Xtest(51,:)*P(:,1:num_pc);
r = [ ];
for i = 1:num_pc
    if S(i)^2/lamda(i) > T2UCL1/num_pc
        r = cat(2,r,i);
    end
end

%2.计算每个变量相对于上述失控得分的贡献
cont = zeros(length(r),X_col);
for i = length(r)
    for j = 1:X_col
        cont(i,j) = abs(S(i)/D(i)*P(j,i)*Xtest(51,j));
    end
end

%3.计算每个变量的总贡献
CONTJ = zeros(X_col,1);
for j = 1:X_col
    CONTJ(j) = sum(cont(:,j));
end

%4.计算每个变量对Q的贡献
e = Xtest(51,:)*(I - P*P');
contq = e.^2;

%5. 绘制贡献图
    figure;
    subplot(2,1,1);
    bar(CONTJ,'k');
    xlabel('变量号');
    ylabel('T^2贡献率 %');
    
    subplot(2,1,2);
    bar(contq,'k');
    xlabel('变量号');
    ylabel('Q贡献率 %');
   
%计算控制限
alpha=0.9;
S=lamda(X_col-num_pc+1:X_col,X_col-num_pc+1:X_col);
FAI=P*pinv(S)*P'/T2UCL1+(eye(X_col)-P*P')/QUCL;
S=cov(Xtrain);
g=trace((S*FAI)^2)/trace(S*FAI);
h=(trace(S*FAI))^2/trace((S*FAI)^2);
kesi =g*chi2inv(alpha,h);
 %% 综合指标
figure;
fai=(Q/QUCL)+(T2/T2UCL1);
plot(fai)
hold on;
line([0,n],[kesi,kesi],'LineStyle','--','Color','r');
title('混合指标');
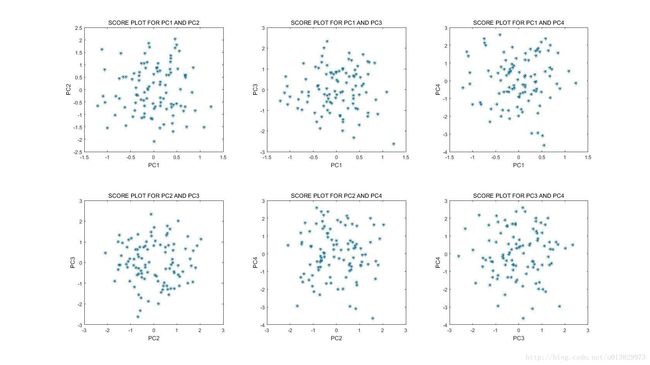
%% 可视化
% 原始得分矩阵可视化
figure;
subplot(2,3,1)
plot(TT(:,1),TT(:,2),'*');
xlabel('PC1');
ylabel('PC2');
title('SCORE PLOT FOR PC1 AND PC2');
subplot(2,3,2)
plot(TT(:,1),TT(:,3),'*');
xlabel('PC1');
ylabel('PC3');
title('SCORE PLOT FOR PC1 AND PC3');
subplot(2,3,3)
plot(TT(:,1),TT(:,4),'*');
xlabel('PC1');
ylabel('PC4');
title('SCORE PLOT FOR PC1 AND PC4');
subplot(2,3,4)
plot(TT(:,2),TT(:,3),'*');
xlabel('PC2');
ylabel('PC3');
title('SCORE PLOT FOR PC2 AND PC3');
subplot(2,3,5)
plot(TT(:,2),TT(:,4),'*');
xlabel('PC2');
ylabel('PC4');
title('SCORE PLOT FOR PC2 AND PC4');
subplot(2,3,6)
plot(TT(:,3),TT(:,4),'*');
xlabel('PC3');
ylabel('PC4');
title('SCORE PLOT FOR PC3 AND PC4');

%% 主元得分可视化
figure;
subplot(2,2,1)
plot(TT1(:,1),TT1(:,2),'*');
xlabel('PC1');
ylabel('PC2');
title('SCORE PLOT FOR PC1 AND PC2');
subplot(2,2,2)
plot(TT1(:,1),TT1(:,3),'*');
xlabel('PC1');
ylabel('PC3');
title('SCORE PLOT FOR PC1 AND PC3');
subplot(2,2,3)
plot(TT1(:,2),TT1(:,3),'*');
xlabel('PC2');
ylabel('PC3');
title('SCORE PLOT FOR PC2 AND PC3');
subplot(2,2,4)
plot3(TT1(:,1),TT1(:,2),TT1(:,3),'*');
xlabel('PC1');
ylabel('PC2');
zlabel('PC3');
grid on;
title('得分矩阵');

程序运行结果（查看高清图片请 双击）：

欢迎评论，顶，点赞！
如有不当之处，请留言，谢谢！