用动态规划玩游戏

---

1. 动态规划之最小路径和

64. 最小路径和

给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

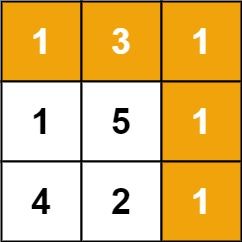
输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。

状态：题目里有，即小人的位置（i，j）
选择： 题目里也有，即每次只能向下或者向右移动一步
dp数组定义： 小人运动到位置（i， j）的时候的最短路径
basecase：初始值左上角0，第一行累加， 第一列累加

class Solution:
    def minPathSum(self, grid: List[List[int]]) -> int:
        Row = len(grid)
        Col = len(grid[0])
        dp = [[float(inf)] * Col for _ in range(Row)]
        #basecase
        rsum = 0
        csum = 0
        for i in range(Row):
            rsum += grid[i][0]
            dp[i][0] = rsum
        for j in range(Col):
            csum += grid[0][j]
            dp[0][j] = csum
        #transition
        for r in range(1, Row):
            for c in range(1, Col):
                dp[r][c] = min(dp[r-1][c], dp[r][c-1]) + grid[r][c]
        return dp[Row-1][Col-1]

2. 动态规划帮我通关了《魔塔》

174.地下城游戏（困难）

一些恶魔抓住了公主（P）并将她关在了地下城的右下角。地下城是由 M x N 个房间组成的二维网格。我们英勇的骑士（K）最初被安置在左上角的房间里，他必须穿过地下城并通过对抗恶魔来拯救公主。

骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下，他会立即死亡。

有些房间由恶魔守卫，因此骑士在进入这些房间时会失去健康点数（若房间里的值为负整数，则表示骑士将损失健康点数）；其他房间要么是空的（房间里的值为 0），要么包含增加骑士健康点数的魔法球（若房间里的值为正整数，则表示骑士将增加健康点数）。

为了尽快到达公主，骑士决定每次只向右或向下移动一步。

编写一个函数来计算确保骑士能够拯救到公主所需的最低初始健康点数。

例如，考虑到如下布局的地下城，如果骑士遵循最佳路径 右 -> 右 -> 下 -> 下，则骑士的初始健康点数至少为 7。

-2 (K)	-3	3
-5	-10	1
10	30	-5 （P）

状态：骑士的位置（i，j）
选择：向右， 向下

dp数组含义：到达该房间时的最少需要多少生命值
basecase：

        rsum = 1
        csum = 1
        for i in range(R):
            rsum += -dungeon[i][0]
            dp[i][0] = max(rsum, 1)
        for j in range(C):
            csum += -dungeon[0][j]
            dp[0][j] = max(csum, 1)

计算第一行和第一列到达某个房间时需要的生命值。但是生命值最少是1
发现这么做行不通没办法算第二行

换一种定义，正着不行就反着来
dp数组含义： 从（i，j）这个房间出发到达右下角终点的时候最少需要多少生命值
basecase:

for i in reversed(range(R-1)):
            dp[i][C-1] = max(1, dp[i + 1][C-1]-dungeon[i][C-1])
for j in reversed(range(C-1)):
            dp[R-1][j] = max(1, dp[R-1][j + 1]-dungeon[R-1][j])

class Solution:
    def calculateMinimumHP(self, dungeon: List[List[int]]) -> int:
        R = len(dungeon)
        C = len(dungeon[0])
        dp = [[0] * C for _ in range(R)]


        dp[R-1][C-1] = max(1, 1-dungeon[R-1][C-1])
        #basecase for last column
        for i in reversed(range(R-1)):
            dp[i][C-1] = max(1, dp[i + 1][C-1]-dungeon[i][C-1])
        for j in reversed(range(C-1)):
            dp[R-1][j] = max(1, dp[R-1][j + 1]-dungeon[R-1][j])

        for i in reversed(range(R-1)):
            for j in reversed(range(C-1)):
                dp[i][j] = max(1, min(dp[i+1][j], dp[i][j+1])-dungeon[i][j])
        return dp[0][0]

3.动态规划帮我通关了《辐射4》

514.自由之路（困难）

电子游戏“辐射4”中，任务“通向自由”要求玩家到达名为“Freedom Trail Ring”的金属表盘，并使用表盘拼写特定关键词才能开门。

给定一个字符串 ring，表示刻在外环上的编码；给定另一个字符串 key，表示需要拼写的关键词。您需要算出能够拼写关键词中所有字符的最少步数。

最初，ring 的第一个字符与12:00方向对齐。您需要顺时针或逆时针旋转 ring 以使 key 的一个字符在 12:00 方向对齐，然后按下中心按钮，以此逐个拼写完 key 中的所有字符。

旋转 ring 拼出 key 字符 key[i] 的阶段中：

您可以将 ring 顺时针或逆时针旋转一个位置，计为1步。旋转的最终目的是将字符串 ring 的一个字符与 12:00 方向对齐，并且这个字符必须等于字符 key[i] 。
如果字符 key[i] 已经对齐到12:00方向，您需要按下中心按钮进行拼写，这也将算作 1 步。按完之后，您可以开始拼写 key 的下一个字符（下一阶段）, 直至完成所有拼写。

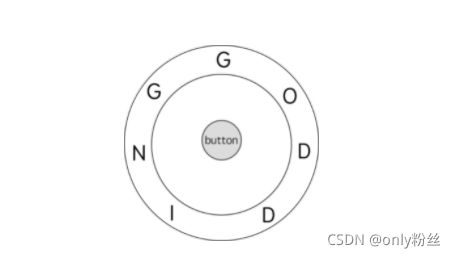
状态：拼完第i个字符， 转盘的指向是ring[j]
选择：下一个转盘的指向
dp数组的含义：dp[i][j] 表示，拼完第i个字符,当前转盘指向是ring[j]时，总共用了多少步
初始化： 都为float(inf)
basecase: 当i 是0时，意味着没有开始时，ring指向第一个，所以dp[0][0] = 0,
除了第一个，剩下的dp[0][1:]都还保持float(inf)
因为当转换到第1个字符的时候只能从ring[0]开始,从ring[1:]开始的都自动加inf，所以完全选择不到。

class Solution:
    def findRotateSteps(self, ring: str, key: str) -> int:
        ring_dict = {}
        for i, s in enumerate(ring):
            if s in ring_dict:
                ring_dict[s].append(i)
            else:
                ring_dict[s] = [i]
        K = len(key)
        R = len(ring)
        # 注意这里有K + 1 行， 因为包括 0 个字符
        dp = [[float(inf)] * (R) for _ in range(K + 1)]
        #basecase: when K is 0, door is pointing to first ring buttom
        dp[0][0] = 0
        for i in range(1, K + 1):
            s_need = key[i-1]
            r_list = ring_dict[s_need]
            # r_cur表示可能选择的ring的位置
            for r_cur in r_list:
            	#计算从哪个位置r_last, 变到当前的r_cur复杂度difficulty最小
                min_value = dp[i][r_cur]
                for r_last in range(R):
                    #compute the difficulty from r_last to r_cur
                    diff = abs(r_cur - r_last)
                    diff = min(diff, R- diff) + 1
                    min_value = min(min_value, diff + dp[i-1][r_last])
                dp[i][r_cur] = min_value
        return min(dp[K])
        

这道题可以看成用手指ring 弹奏乐谱key，只不过对乐谱的音符，只能选择某些手指弹奏

4. 旅游省钱大法：加权最短路径

787. K 站中转内最便宜的航班

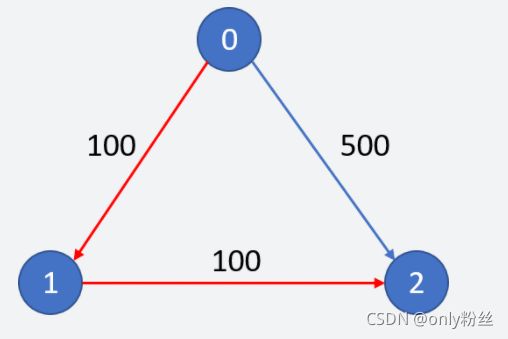
有 n 个城市通过一些航班连接。给你一个数组 flights ，其中 flights[i] = [fromi, toi, pricei] ，表示该航班都从城市 fromi 开始，以价格 pricei 抵达 toi。

现在给定所有的城市和航班，以及出发城市 src 和目的地 dst，你的任务是找到出一条最多经过 k 站中转的路线，使得从 src 到 dst 的 价格最便宜 ，并返回该价格。 如果不存在这样的路线，则输出 -1。

输入:
n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]]
src = 0, dst = 2, k = 1
输出: 200
解释:
城市航班图如下

状态：当前到达城市， 最多用几次
选择：出发城市
这次用自顶向下的方法dp(dst, k) 表示当前到达dst城市时最多用k步的cost
选择:

dp(dst, k) = min(
    dp(s1, k - 1) + w1, 
    dp(s2, k - 1) + w2
)

# basecase 有三个
if i == -1:
    return float(inf) # 用光了步数
if d == src:
    return 0 # 到达了初始点
if d not in dst_src:
    return float(inf) # 没有到d 的飞机

class Solution:
    def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, k: int) -> int:
        k = k + 1# 把有多少中转站转换成有多少步
        dst_src = {}
        for e in flights:
            d = e[1]
            s = e[0]
            cost = e[2]
            if d in dst_src:
                dst_src[d].append([s, cost])
            else:
                dst_src[d] = [[s, cost]]
        memo = {}
        def dp(d, i, memo):
            if (d, i) in memo:
                return memo[(d, i)]
            if i == -1:
                return float(inf)
            if d == src:
                return 0
            if d not in dst_src:
                return float(inf)
            res = float(inf)
            for s, cost in dst_src[d]:
                res = min(dp(s, i-1, memo) + cost, res)
            memo[(d,i)] = res
            return res
        return -1 if dp(dst, k, memo) == float(inf) else dp(dst, k, memo)

5. 经典动态规划：正则表达式

10.正则表达式匹配（困难）

给你一个字符串 s 和一个字符规律 p，请你来实现一个支持 ‘.’ 和 ‘*’ 的正则表达式匹配。

‘.’ 匹配任意单个字符
‘*’ 匹配零个或多个前面的那一个元素
所谓匹配，是要涵盖 整个 字符串 s的，而不是部分字符串。

示例 1：
输入：s = “aa” p = “a”
输出：false
解释：“a” 无法匹配 “aa” 整个字符串。

示例 2：
输入：s = “aa” p = “a*”
输出：true
解释：因为 ‘*’ 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 ‘a’。因此，字符串 “aa” 可被视为 ‘a’ 重复了一次。

状态：当前匹配到字符串s 和 p 的位置
选择：‘*’表示几次前一个字符， 可以表示0次 或者多次

当前字符match
if s[i] == p[j] or p[j] == '.':
	下一个字符是‘*’可以表示0个当前字符，或者多个
      if j < plen -1 and p[j + 1] == '*':
          res = dp(i + 1, j, memo) or dp(i, j + 2, memo)
      else:
          res = dp(i + 1, j + 1, memo)
当前字符not match
else:
	下一个字符是‘*’只可以表示0个当前字符
      if j < plen -1 and p[j + 1] == '*':
          res = dp(i, j + 2, memo)
      else:
          res = False

class Solution:
    def isMatch(self, s: str, p: str) -> bool:
        slen = len(s)
        plen = len(p)
        memo = {}
        def dp(i, j, memo):
            #basecase
            if j == plen:
                return i == slen
            if i == slen:
                if (plen - j) %2 != 0:
                    return False
                else:
                    # x*y*z*
                    for j_star in range(j + 1, plen, 2):
                        if p[j_star] != '*':
                            return False
                    return True
            res = False
            if s[i] == p[j] or p[j] == '.':
                if j < plen -1 and p[j + 1] == '*':
                    res = dp(i + 1, j, memo) or dp(i, j + 2, memo)
                else:
                    res = dp(i + 1, j + 1, memo)
            else:
                if j < plen -1 and p[j + 1] == '*':
                    res = dp(i, j + 2, memo)
                else:
                    res = False
            memo[(i,j)] = res
            return res
        return dp(0,0, memo)

6. 经典动态规划：高楼扔鸡蛋

887.鸡蛋掉落（困难）

解法一：
状态： 需要验证i层楼， 有j个鸡蛋
选择：当给定状态的时候，在哪层扔， 是最优策略（choice）
dp[i][j]: 表示有 i 个鸡蛋，要验证 j 层的楼时，最坏情况的最小操作数
basecase：
dp[1][…] = i 表示最坏情况只有1个鸡蛋只能从顶楼一直扔到1楼，因为碎了就没得扔了
dp[…][0] = 0 表示楼是0层的时候不用扔

class Solution:
    def superEggDrop(self, k: int, n: int) -> int:
        dp = [[float('inf')] * (n+1) for _ in range(k+1)]
        dp[1] = list(range(n + 1))# 如果只有一个鸡蛋
        for i in range(k + 1): # 如果是0层
            dp[i][0] = 0
        
        for i in range(2, k + 1):
            for j in range(1, n + 1):
                #如果从3楼扔，没碎的话dp[i][j] = dp[i][j-3] #注意这里是j因为当前总共验证j层楼
                #如果从3楼扔，碎了的话dp[i][j] = dp[i-1][3-1]
                for choice in range(1, j + 1):
                    dp[i][j] = min(dp[i][j], 1 + max(dp[i][j-choice], dp[i-1][choice-1]))
        #print(dp)
        return dp[k][n]

注意这里用的是线性扫描来找到最优的策略，会超时

for choice in range(1, j + 1):
    dp[i][j] = min(dp[i][j], 1 + max(dp[i][j-choice], dp[i-1][choice-1]))

那就用二分法

class Solution:
    def superEggDrop(self, k: int, n: int) -> int:
        dp = [[float('inf')] * (n+1) for _ in range(k+1)]
        dp[1] = list(range(n + 1))# 如果只有一个鸡蛋
        for i in range(k + 1): # 如果是0层
            dp[i][0] = 0
        
        for i in range(2, k + 1):
            for j in range(1, n + 1):
                #如果从3楼扔，没碎的话dp[i][j] = dp[i][j-3]
                #如果从3楼扔，碎了的话dp[i][j] = dp[i-1][3-1]
                # for choice in range(1, j + 1):
                #     dp[i][j] = min(dp[i][j], 1 + max(dp[i][j-choice], dp[i-1][choice-1]))               
                res = float('inf')
                lo, hi = 1, j
                while lo <= hi:
                    choice = lo + (hi - lo) //2
                    broke = dp[i-1][choice-1]
                    not_broke = dp[i][j-choice]
                    if broke > not_broke:
                        hi = choice -1
                        res = min(res, broke + 1)
                    else:
                        lo = choice + 1
                        res = min(res, not_broke + 1)
                dp[i][j] = res
        #print(dp)
        return dp[k][n]

竟然会超时
用一下原文的备忘录方法

class Solution:
    def superEggDrop(self, k: int, n: int) -> int:
        memo = {}
        def dp(i, j): #i 个鸡蛋 j 层楼
            if (i, j) in memo:
                return memo[(i,j)]
            if i == 1:
                return j
            if j == 0:
                return 0
            res = float('inf')
            lo, hi = 1, j
            while lo <= hi:
                choice = lo + (hi - lo)//2
                broke = dp(i-1, choice -1)
                not_broke = dp(i, j - choice)
                if broke > not_broke:
                    hi = choice -1
                    res = min(res, broke + 1)
                else:
                    lo = choice + 1
                    res = min(res, not_broke + 1)

            memo[(i,j)] = res
            return res
        return dp(k,n)

还有一种比较有意思的方法：
我们可以改变一下状态，确定当前的鸡蛋个数和最多允许的扔鸡蛋次数，就知道能够确定 F 的最高楼层数

dp[k][m] = n
# 当前有 k 个鸡蛋，可以尝试扔 m 次鸡蛋
# 这个状态下，最坏情况下最多能确切测试一栋 n 层的楼

# 比如说 dp[1][7] = 7 表示：
# 现在有 1 个鸡蛋，允许你扔 7 次;
# 这个状态下最多给你 7 层楼，
# 使得你可以确定楼层 F 使得鸡蛋恰好摔不碎
# （一层一层线性探查嘛）

但是这种方法也有个问题就是不能获得一种策略，只能计算次数。上面那种方法可以知道在面对某种状况的时候， 用哪个choice可以得到最优

class Solution:
    def superEggDrop(self, k: int, n: int) -> int:
        #k eggs, m throws
        m = n
        dp = [[0] * (m + 1) for _ in range(k + 1)]
        
        for j in range(1, m + 1):
            for i in range(1, k+ 1):
                dp[i][j] = dp[i-1][j-1] + dp[i][j-1] + 1
                if dp[i][j] >= n:
                    return j
        return -1

空间优化一下

class Solution:
    def superEggDrop(self, k: int, n: int) -> int:
        #k eggs, m throws
        dp = [0] * (k + 1)
        m = 1
        while True:
            pre = dp[0]
            for i in range(1, k+ 1):
                cur = dp[i]
                dp[i] = pre + dp[i] + 1
                pre = cur
                if dp[i]>= n:
                    return m
            m += 1   
        return -1

7. 经典动态规划：戳气球

312. 戳气球

这道题可以反着看，从没有气球， 逐一添加，到气球是初始nums能得到的分数
状态：开区间（i，j）中全部添加了气球时得到的金币
选择：添加[i + 1, i + 2, … , j-1]中的哪个气球
basecase：当 i+1==j 时开区间中没有元素所以金币数为0
注意， 首先要在nums两端加上dummy 的1

class Solution:
    def maxCoins(self, nums: List[int]) -> int:
        n = len(nums)
        nums = [1] + nums + [1]
        memo = {}
        def dp(i, j):
            if (i, j) in memo:
                return memo[(i,j)]
            if i + 1 == j:
                return 0
            res = 0
            for k in range(i + 1, j):
                res = max(res, dp(i, k) + dp(k, j) + nums[k] * nums[i] * nums[j])
            memo[(i,j)] = res
            return res
        return dp(0, n + 1)

自下而上的版本

class Solution:
    def maxCoins(self, nums: List[int]) -> int:
        n = len(nums)
        rec = [[0] * (n + 2) for _ in range(n + 2)]
        val = [1] + nums + [1]
        # 0,1,...,n,n-1,n, n+1
        for i in reversed(range(n)):
            for j in range(i + 2, n + 2):
                for k in range(i + 1, j):
                    total = val[i] * val[k] * val[j]
                    total += rec[i][k] + rec[k][j]
                    rec[i][j] = max(rec[i][j], total)
        return rec[0][n + 1]

8. 经典动态规划：博弈问题

877. 石子游戏

状态：剩下的石堆从第 i 到 j ， 先手还是后手
选择：选开头还是结尾的石头
dp(i, j, k): 在从（i，j）的石堆中是先手(k = 0) 时可以获得的分数

class Solution:
    def stoneGame(self, piles: List[int]) -> bool:
        memo = {}
        def dp(i, j, k):
            if (i,j,k) in memo:
                return memo[(i,j,k)]
            if i == j: #只有一个石头
                if k == 0:
                    return piles[i]
                else:
                    return 0
            left = piles[i] + dp(i + 1, j,1)
            right = piles[j] + dp(i, j-1, 1)
            if left > right:
                memo[(i,j,0)], memo[(i,j,1)] = left, dp(i + 1, j, 0)
            else:
                memo[(i,j,0)], memo[(i,j,1)] = right, dp(i, j - 1, 0)
            
            return memo[(i,j,k)]
        return dp(0, len(piles)-1, 0) > dp(0, len(piles)-1, 1)

9. 经典动态规划：四键键盘

经典动态规划：四键键盘

比较好想的一种状态
状态：剩余按键次数， 屏幕A的个数， bufferA的个数
选择：按哪个按键
dp含义：给定状态下， 屏幕上A的个数

def keyboard(N:int)->int:
    memo = {}
    def dp(n,screen, buffer):
        if (n, screen, buffer) in memo:
            return memo[(n, screen, buffer)]
        if n <= 0:
            return screen
        a = dp(n-1, screen + 1, buffer)
        ctrl_ac = dp(n-2, screen, screen)
        ctrl_v = dp(n-1, screen + buffer, buffer)
        res = max(a, ctrl_ac, ctrl_v)
        memo[(n, screen, buffer)] = res
        return res
    return dp(N,0,0)

时间复杂度太高
dp[n][a_num][copy]
状态的总数（时空复杂度）就是这个三维数组的体积，但是a_num和copy都很大

另一种思路
状态只有剩余按键次数
选择：1.按A键， 2. 连续按ctrl_a, ctrl_c, ctrl_v, ctrl_v(也就是按ctrl_v的次数 + 2)

def keyboard2(N:int)->int:
    memo = {}
    def dp(n):
        if (n) in memo:
            return memo[(n)]
        if n <= 0:
            return 0
        a = dp(n-1) + 1
        #另一种情况 ctrl_a, ctrl_c, ctrl_v, ctrl_v....
        i = 1 # ctrl_v 的次数是1
        keys = 2 + i #需要加上前面的 ctrl_a, ctrl_c
        res = a
        while keys <= n:
            res = max(res, dp(n-keys) * (i + 1))
            i += 1
            keys = 2 + i
        memo[(n)] = res
        return res
    return dp(N)

10. 团灭 LEETCODE 股票买卖问题

188. 买卖股票的最佳时机 IV

状态：进行到第 i 天， 手中是否持有股票0，1， 还有几次交易机会k
选择：当持有股票时， 是否卖出， 当没有股票时是否选择买入

class Solution:
    def maxProfit(self, k: int, prices: List[int]) -> int:
        memo = {}
        def dp(i, j, kk):
            if (i,j,kk) in memo:
                return memo[(i,j,kk)]
            if i == 0:
                if j == 1:
                    return -float('inf')
                if j == 0:
                    return 0
            if kk < 0:
                return -float('inf')

            if j == 0:
                res = max(dp(i-1, 0, kk), dp(i-1, 1, kk-1) + prices[i-1]) 
                memo[(i,0,kk)] = res
            else:
                res = max(dp(i-1, 1, kk), dp(i-1, 0, kk) - prices[i-1])
                memo[(i,1,kk)] = res
            return res
        return dp(len(prices), 0, k)

11. 团灭 LEETCODE 打家劫舍问题

198. 打家劫舍

状态：偷到第几家
选择：当前这家偷还是不偷

class Solution:
    def rob(self, nums: List[int]) -> int:
        memo = {}
        def dp(i):
            if i < 0:
                return 0
            if i in memo:
                return memo[i]
            res = max(dp(i-1), dp(i-2) + nums[i])
            memo[i] = res
            return res
        return dp(len(nums) -1)

213. 打家劫舍 II

和上面的基本一样
只不过是把圈拆成两个队列， 然后取其中较大的

class Solution:
    def rob(self, nums: List[int]) -> int:
        #special case
        if len(nums) == 1:
            return nums[0]
        nums1, nums2 = nums[:-1], nums[1:]
        def _rob(nums: List[int]) -> int:
            memo = {}
            def dp(i):
                if i < 0:
                    return 0
                if i in memo:
                    return memo[i]
                res = max(dp(i-1), dp(i-2) + nums[i])
                memo[i] = res
                return res
            return dp(len(nums) -1)
        return max(_rob(nums1), _rob(nums2))

337. 打家劫舍 III

这次问题变成了树，有点棘手了
状态：偷到哪个节点
选择：对当前这个节点是偷还是不偷
dp() 含义： 从当前节点开始偷，偷完由当前节点构成的子树后能获得的最大值

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def rob(self, root: TreeNode) -> int:
        memo = {}
        def dp(cur_root: TreeNode) -> int:
            if cur_root in memo:
                return memo[cur_root]
            if cur_root is None:
                return 0
            # 如果枪这个节点
            money = cur_root.val
            if cur_root.left:
                money += dp(cur_root.left.left) + dp(cur_root.left.right)
            if cur_root.right:
                money += dp(cur_root.right.left) + dp(cur_root.right.right)

            #如果不抢这个节点
            money2 = dp(cur_root.left) + dp(cur_root.right)
            memo[cur_root] = max(money, money2)
            return memo[cur_root]
        return dp(root)

其实就相当于这么看，要算dp(root)可以递归到最左边， basecase：节点是None的时候输出0
只不过多了几条路径，这道题里不同路径因为都可以抢， 都加起来就可以了。

12. 有限状态机之 KMP 字符匹配算法

28.实现 strStr(简单)

先在开头约定，本文用 pat 表示模式串，长度为 M，txt 表示文本串，长度为 N。KMP 算法是在 txt 中查找子串 pat，如果存在，返回这个子串的起始索引，否则返回 -1。
本文用一个二维的 dp 数组（但空间复杂度还是 O(M)），重新定义其中元素的含义，使得代码长度大大减少，可解释性大大提高。

// 暴力匹配（伪码）
int search(String pat, String txt) {
    int M = pat.length;
    int N = txt.length;
    for (int i = 0; i <= N - M; i++) {
        int j;
        for (j = 0; j < M; j++) {
            if (pat[j] != txt[i+j])
                break;
        }
        // pat 全都匹配了
        if (j == M) return i;
    }
    // txt 中不存在 pat 子串
    return -1;
}

可以看见对于每一个 i， 都需要比较M次，当比较不成功的时候都需要回退指针从i+1开始比较
KMP 算法永不回退 txt 的指针 i，不走回头路（不会重复扫描 txt），而是借助 dp 数组中储存的信息把 pat 移到正确的位置继续匹配

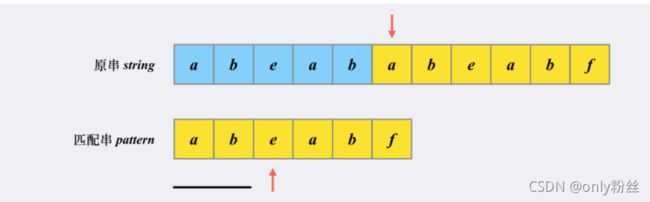
KMP 算法的难点在于，如何计算 dp 数组中的信息？如何根据这些信息正确地移动 pat 的指针？

计算这个 dp 数组，只和 pat 串有关
状态：当前的位置 i

dp数组含义： dp[i] = k 表示以 i 结尾长度为 k + 1 的子串(以i - k开头，以i结尾的子串)，和从pat开头长度为 k + 1 的子串（以0开头k结尾的子串）是相同的且在所有相同的里面最长的，以上图为例， dp[4] = 1, dp[3] = 0，这样的话从pat[i] 往下匹配和从pat[k] 往下匹配是完全等价的
如果从头都不相等，就返回-1， 例如dp[2] = -1

假设已知dp[i-1] = k 表示当匹配到 i-1 的时候，从开头能匹配到k，
首先，我们可以查看pat[k+1] 和 pat[i]， 如果相等那就说明又成功匹配了一个所以dp[i] = dp[i-1] + 1 = k + 1
如果不相等， 我们可以接着看dp[dp[i-1]] = dp[k] = kk假设是kk，dp[k] = kk 表示当匹配到 k 的时候，从开头能匹配到kk，我们可以查看pat[kk+1] 和 pat[i]， 如果相等那就说明成功匹配了一个所以dp[i] = dp[dp[i-1]] + 1 = kk + 1, 如果不相等就再加一层dp

首先根据pat，算出next数组

class Solution:
    def strStr(self, haystack: str, needle: str) -> int:
        pat = needle
        txt = haystack

        def kmp(pat):
            next = [-1] * len(pat)
            for i in range(1, len(pat)):
                k = next[i-1] 
                while True:
                    if pat[i] == pat[k + 1]:
                        next[i] = k + 1
                        break
                    else:
                        if k == -1:
                            break
                        else:
                            k = next[k]
            return next

        if pat == '':
            return 0
        next = kmp(pat)
        i, j = 0,0
        while i < len(txt):
            if pat[j] == txt[i]:
                j += 1
                i += 1
                if j == len(pat):
                    return i - len(pat)
            else:
                if j > 0:
                    j = next[j-1] + 1 
                else:
                    i += 1
        return -1

13. 构造回文的最小插入次数

1312. 让字符串成为回文串的最少插入次数

常规操作
状态：从 i 到 j 的字符串
选择：当s[i] == s[j]的时候，dp(i,j) = dp(i+1, j - 1)
当 s[i] != s[j] 的时候， dp(i,j) = min(dp(i+1,j), dp(i, j-1)) + 1
dp(i, j-1)的意思是把s[i…j-1] 变成回文串的代价，就是相当于在j的位置添加一个s[i]

class Solution:
    def minInsertions(self, s: str) -> int:
        n = len(s)
        dp = [[0] * n for _ in range(n)]
        for i in range(n):
            dp[i][i] = 0 
        for i in reversed(range(n-1)):
            for j in range(i+1, n):
                if s[i] == s[j]:
                    dp[i][j] = dp[i+1][j-1]
                else:
                    dp[i][j] = min(dp[i+1][j], dp[i][j-1]) + 1
        return dp[0][n-1]