辨析梯度下降

前言

梯度下降是最为常用的深度学习模型优化算法。本文对经典的梯度下降、随机梯度下降、批量随机梯度下降进行分别解释，帮助区分三者之间的关系。最后以线性回归为例，根据模型优化结果分析了三者的特点。
完整代码已上传至：github完整代码

一、梯度下降（Gradient Descent, GD)

1.1 梯度下降的本质

梯度下降法是一种参数优化方法。
优化：是指改变参数$x$以最小化或最大化某函数$f(x)$。通常，以最小化$f(x)$指代大多数优化问题，而最大化可由取相反数转化为最小化问题，即$\underset{x}{\max }[f(x)]\iff \underset{x}{\min }[-f(x)]$。

e.g. 负对数似然函数即对原始似然函数取对数后，再取相反数，将最大化似然函数转化为最小化负对数似然函数。¹

1.2 梯度下降的思想

梯度下降法的基本思想：沿着负梯度方向搜索最优解。

因为负梯度方向是函数值下降最快的方向。²

1.3 梯度下降的计算

每一次迭代中，按照学习率$\alpha$沿梯度的反方向更新参数，直至收敛，公式表达为：
$$\theta (n+1)=\theta (n)-\alpha \frac{df}{d\theta (n)}$$

二、深度学习优化算法

梯度下降是深度学习中最为常用的优化算法，但根据每次更新参数使用的样本数量的不同，划分为：梯度下降法、随机梯度下降法、批量随机梯度下降法。

2.1 经典的梯度下降法

假设已知$m$个样本及其标签$(x_1,y_1),(x_2,y_2),...,(x_m,y_m)$，模型对每个样本的预测值为${\hat{y}}_i,i=1,2,...,m$。

1. 单个样本$(x_i,y_i)$的损失为：
   $$los{s}_i({\theta }_1,{\theta }_2)=F({\theta }_1,{\theta }_2;y_i,{\hat{y}}_i)$$
   式中，$F({\theta }_1,{\theta }_2)$为模型的损失函数，这里梯度下降通过优化参数${\theta }_1,{\theta }_2$最小化损失函数。

• 损失函数用于衡量模型预测值与样本真实值之间的差别；
• 在深度学习中，梯度下降法用于最小化损失函数；
• 常用的损失函数：均方误差(Mean Square Error, MSE)损失、交叉熵(Cross Entropy Loss)损失。

2. 所有样本的平均损失为：
   $$Loss({\theta }_1,{\theta }_2)=\frac{1}{m}\sum _{i=1}^{m}los{s}_i({\theta }_1,{\theta }_2)$$
3. 参数更新：
   对于参数${\theta }_1$：${\theta }_1(n+1)={\theta }_1(n)-\alpha \frac{\partial Loss}{\partial {\theta }_1}$
   对于参数${\theta }_2$：${\theta }_2(n+1)={\theta }_2(n)-\alpha \frac{\partial Loss}{\partial {\theta }_2}$
   这里，进行参数更新时，使用的是所有样本损失的平均值。

经典的梯度下降法每进行一次迭代都需要计算所有样本的损失，当样本量很大（e.g. ImageNet包含128万个训练样本）时，会非常消耗计算资源，且存在以下不足：

• 收敛速度慢，需要迭代的次数（epoch)多；
• 每次计算同时考虑了所有训练样本，丧失随机性，容易造成过拟合。

于是，随机梯度下降的思想应运而生。

2.2 随机梯度下降法(Stochasitc Gradient Descent, SGD)

随机梯度下降的基本思想：每次只计算一个样本的损失，然后遍历所有样本，完成一轮（epoch）迭代。
随机梯度下降算法描述：

for epoch in range(epochs):  # 共运行epochs轮
  for i in range(m):  # 每次迭代遍历1个样本
    $Loss({\theta }_1,{\theta }_2)=F({\theta }_1,{\theta }_2;{\hat{y}}_i,y_i)$  # 计算单个样本的损失
    ${\theta }_1(n+1)={\theta }_1(n)-\alpha \frac{\partial Loss}{\partial {\theta }_1}$  # 使用单个样本的损失更新参数
    ${\theta }_2(n+1)={\theta }_2(n)-\alpha \frac{\partial Loss}{\partial {\theta }_2}$
  end
end

随机梯度下降相较于经典的梯度下降算法在计算速度上有了很大提升，但由于每次迭代只计算一个样本的损失，导致损失波动很大。

1.3 批量随机梯度下降(mini_batch SGD)

批量随机梯度下降的基本思想：每次迭代选取总训练样本的一小部分（即一个batch)，计算其平均损失的梯度来优化参数，完成对所有训练样本的迭代为一个epoch。

批量随机梯度下降可描述为：

for epoch in range(epochs):
 for batch in range(batches):
   $Loss(\theta ,{\theta }_2)=\frac{1}{b}{\sum }_{i=1}^{b}F({\theta }_1,{\theta }_2;y_i,{\hat{y}}_i)$   # b为一个batch包含的样本数量
    ${\theta }_1(n+1)={\theta }_1(n)-\alpha \frac{\partial Loss}{\partial {\theta }_1}$  # 使用一个batch的样本的平均损失更新参数
    ${\theta }_2(n+1)={\theta }_2(n)-\alpha \frac{\partial Loss}{\partial {\theta }_2}$
 end
end

与随机梯度下降相比，批量随机梯度下降可以缓解其损失的波动，使计算结果不容易受某单个样本的影响；与经典的梯度下降相比，批量随机梯度下降每次迭代仅计算小批量的样本的损失，减少了计算资源的占用。

三、代码实现

以线性回归为例，分别使用梯度下降、随机梯度下降和小批量随机梯度下降算法优化模型参数。

3.1 生成数据集

根据带有噪声的线性模型构造人造数据集，生成数据的线性模型为：
$$\mathbf{y}=\mathbf{X}\mathbf{w}+\mathbf{b}+ϵ$$
式中，$\mathbf{w},\mathbf{b}$为模型参数，$ϵ$为样本中存在的噪声，假设噪声符合均值为0，方差为0.5的正态分布。

'''生成数据集'''
def synthetic_data(w, b, num_examples):
    X = torch.normal(0, 1, (num_examples, len(w)))
    y = torch.matmul(X, w) + b
    y += torch.normal(0, 0.5, y.shape)
    return X, y.reshape((-1,1))

'''生成数据并绘制'''
true_w = torch.tensor([3.5])
true_b = 4
features, labels = synthetic_data(true_w, true_b, 1000)
plt.plot(features.numpy(), labels.numpy(), 'b.', label='train data')
true_y = torch.matmul(features, true_w) + true_b
plt.plot(features.numpy(), true_y.reshape((-1,1)).numpy(), 'r-', label='true line')
plt.show()

3.2 定义回归模型

def line_regression(X, w, b):
    return torch.matmul(X, w) + b

3.3 定义损失函数

使用平均方差损失函数：
$$loss=\frac{1}{2m}\sum _{i=1}^m(\hat{y}-y{)}^2$$
式中，$m$为每次计算损失用到的样本数量。

def squared_loss(y_hat, y, batch_size):
	"""
	batch_size = num_examples时，为经典的梯度下降算法
	batch_size = 1时，为随机梯度下降算法
	batch_size in range(2, num_examples)时，为批量随机梯度下降
	"""
    return (y_hat - y.reshape(y_hat.shape)) ** 2 / (2 * batch_size)

3.4 定义优化算法

def sgd_optimizer(params, lr):
    with torch.no_grad():
        for param in params:
            param -= lr * param.grad
            param.grad.zero_()

3.5 模型训练

'''初始化模型参数'''
w = torch.normal(0, 0.01, size=(1, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
'''初始化超参数'''
lr = 0.02
num_epochs = 50
batch_size = 50
loss = squared_loss
sgd = sgd_optimizer
net = line_regression
for epoch in range(num_epochs):
    for X, y in data_iter(train_data, train_labels, batch_size):
        l = loss(net(X, w, b), y, batch_size)
        l.sum().backward()
        sgd([w, b], lr)
    with torch.no_grad():
        train_l = loss(net(train_data, w, b), train_labels, len(train_data))
        print('epoch', epoch, ' loss ', float(train_l.sum()))

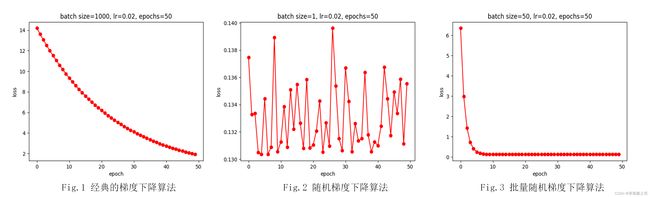
3.6 模型训练结果

观察训练结果图可验证以下结论³：

1. 经典的梯度下降算法收敛慢，需要迭代更多epoch才能得到更小的损失；

自我思考：
  可以从参数更新的次数的角度解释为什么经典的梯度下降算法需要更多的epochs。
  因为经典的梯度下降算法每次迭代都需要计算所有样本的损失，取其平均值之后，进行反向传播，更新参数，所以，这里参数更新（反向传播）的次数$=numofepochs$。而随机梯度下降参数更新（反向传播）的次数$=numofepochs\times numofexamples$; 批量随机梯度下降参数更新（反向传播）的次数$=numofepochs\times \frac{numofexamples}{batchsize}$
但是epochs的选取与优化的起点（参数初始化）、学习率的选取、样本所含噪声、模型的设计及损失函数的定义等都有关系，参数更新（反向传播）的次数或许是原因之一。

3. 相同学习率的情况下，随机梯度下降算法的损失波动较大，结果在最优值附近反复跳动；
4. 相比之下，批量随机梯度下降收敛更快，且波动小，但需要选择合适的batch size，且需要权衡batch size与epochs使得训练结果、训练速度达到相对最优。

---

1. 深入理解交叉熵损失函数 ↩︎

2. 为什么梯度的负方向是局部下降最快的方向？ ↩︎

3. 梯度下降法(SGD)原理解析及其改进优化算法 ↩︎