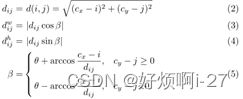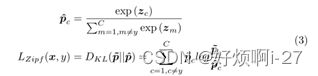有关深度学习中的目标检测论文阅读
第一篇论文是Towards Accurate Oriented Object Detection in Complex Environments ECCV 2020
主要解决的是目标检测的问题。
由于现有OBB方法大多基于水平边界盒检测器，通过引入距离损失优化的附加角度维度，其中距离损失仅使OBB的角度误差最小化，并且与IoU松散相关，对具有高纵横比的对象不敏感，提出一种新损失，像素IoU（PIoU）损失，以利用角度和IoU进行准确的OBB回归。PIoU损失是从具有像素形式的IoU度量导出的，该度量简单且适用于水平和定向边界框。
与标准距离损失相比，PIoU损失直接反映了IoU及其局部最优值。原理是IoU损耗通常比距离损耗实现更好的性能。设计了一个RoI变换器来学习从BB到OBB的变换，然后提取旋转不变特征。制定了生成概率模型以提取OBB提案，对每个提案，通过搜索局部最大似然来确定位置、大小和方向。PIoU损失计算是通过累积内部重叠像素的贡献来直接计算IoU，掩模损失是通过每像素S形的平均二进制交叉熵（S形交叉熵损失）来计算的，是基于正IoU来计算，保留两个框之间的相交和并集区域，在每个区域中，像素的贡献根据其空间信息进行建模和累积。
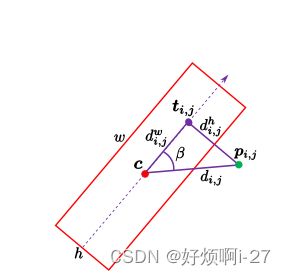
利用一下公式可以判断Pi,j是否在bounding box中需要计算三角形3个边的长度，利用以上的bounding box的label（Cx，Cy，w，h，θ）以及点Pi,j的坐标（i，j），可以算出三条边的长度分别为：
由于计算的包含bounding box b以及Ground Truth b’的最小水平框中的点，在这种情况下对于计算丝毫不相交的有劣势，对应的面积会很大，可以做一个预处理看两个最小水平框是否存在交集：
由于其中的δ函数不可导，使用核函数来替换δ函数：
核函数K(d,s)的表达形式如下所示：
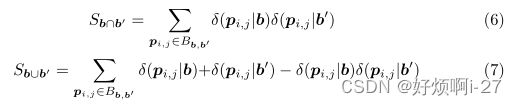
其中F满足当Pi,j在b中取值接近于1，当不在b中时，取值接近于0，将原来式子中的δ 用F函数替换得到：
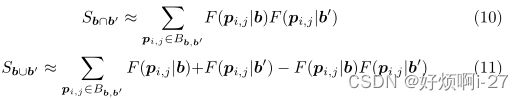
利用交集和并集之间的关系，计算Sb∪b′，从而减少一定的计算量：
提出的PIoU的计算可以表示为：
设b为预测框，b0为地面真值框，如果预测框b基于正锚点，则将一对（b，b0）视为正，并且b0是匹配的地面真值框。使用M表示所有的正对的集合，为了最大化b和b0之间的PIoU，拟定PIoU损失计算如下：
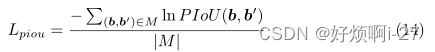
第二篇是
Efficient One Pass Self-distillation with Zipf’s Label Smoothing ECCV 2022 旷世科技（基于Zipf分布实现标签平滑的高效单程自蒸馏方法）
本文提出了一种名为Zipf标签平滑（标签平滑作用防止过拟合）（Zipf’s LS）的高效自蒸馏方法，该方法使用网络的动态预测来生成符合Zipf分布的软监督，不使用任何对比样本或辅助参数。来源：实验观察当网络被适当训练时，网络的最终softmax层的输出值，在按大小排序并在样本间平均后，应遵循自然语言词频统计中类似于齐普夫定律（把一篇较长文章中每个词出现的频次统计起来，按照高频词在前、低频词在后的递减顺序排列，并用自然数给这些词编上等级序号，即频次最高的词等级为1，若用f表示频次，r表示等级序号，则有fr=C（C为常数）。人们称该式为齐普夫定律）的分布，通过在样本水平上和整个训练期间实施该特性，可以提高预测精度。
Zipf定律：指出元素的归一化频率应与元素的等级成反比，用一个方程式来描述如下：
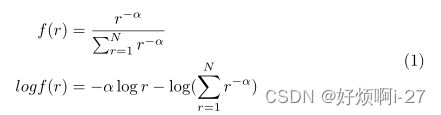
r是元素的秩，N是元素的总数，f是频率，α是大于0的常数，控制衰变率。当网络被训练到其收敛状态时，softmax网络输出遵循Zifp定律。
通过直接对样本的softmax预测进行排序（基于logit排序方法）来正确地对输出类别进行排序。图像样本x和标签y的Zipf损失LZipf被定义为归一化非目标预测与从密集分类排序生成的合成Zipf软标签之间的KL散度：
接着
由于非目标类c的合成Zipf标签˜p应遵循Zipf定律的等式，具有相应的秩Rc：
α是控制分布形状的超参数
LCE是具有one-hot ground-truth标签的标准交叉熵损失，组合损失函数如下：
与统一标签平滑的比较，Lzipf与Lls相对于非目标逻辑的梯度如下所示：
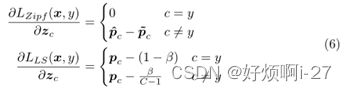
（1-β）表示目标类，C是类的总数，标签平滑抑制了高排名类的预测，或将低排名类的预期提升到了相同的水平，β是恒定的与排名无关。
第三篇是Arbitrary-oriented object detection with circular smooth label.ECCV, 2020.（基于圆形平滑标签的任意定向目标检测）
由角周期性或角排序直接导致的基于回归的旋转检测器存在边界不连续的问题，发现根原是理想的预测超出了定义的范围，设计一种新的旋转检测基线，亮点：①通过将角度预测从回归问题转换为精度损失很小的分类任务来解决边界问题，设计了一个新的旋转检测基线。②还提出一种圆形平滑标签（CSL）技术来处理角度的周期性并增加对相邻角度的误差容限，解决边界不连续的问题。③进一步在CSL中引入了四个窗口函数，并探讨了不同窗口半径大小对检测性能的影响。
从回归到分类的转换可能会导致一定的准确性损失，采用五参数法180°以角度范围为例，ω（默认ω=1°）每个间隔的度数指的是一个类别。可以计算最大精度损失Max（损失）和预期精度损失E（损失）：
由此可以得出旋转检测器的损失很小。
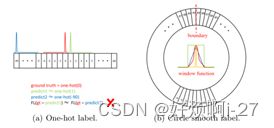
One-hot标签在旋转检测方面有两个缺点：
①边界框使用90°基于回归的方法有两种不同的边界情况（垂直和水平），180°基于回归的方法只有垂直边界情况。
②普通分类损失与预测标签和地面真实标签之间的角度距离无关，因此不适合角度预测问题。分类器的预测结果为1°和-90°，预测损失是相同的，但从检测角度来看，应该允许接近地面真实的预测结果。
设计了一种圆形平滑标签（CSL）技术，以通过分类获得更鲁棒的角度预测，而不受边界条件的影响，包括EOE和PoA。CSL表达公式如下：
r是g(x)的半径，θ表当前边界框的角度。
理想的g(x)需要保持以下性质：
-
周期性：g(x)=g(x+kT) ,k∈ N、 T=180/ω，表示角度被划分的数量，默认值为180
-
对称性：0≤ g（θ+ε）=g（θ−ε) ≤ 1，|ε|
-
单调：0≤ g（θ±ε）≤ g（θ±ς）≤ 1，|ς|<|ε|
给出满足上述三个性质的四个有效g(x)：脉冲函数、矩形函数、三角形函数和高斯函数。标签值在边界处是连续的，并且由于CSL的周期性，当窗口函数是脉冲函数或窗口函数的半径很小时，一个one-hot相当于CSL。
这里的多任务管道包含基于回归的预测分支和基于CSL的预测分支，以便于在同等基础上比较两种方法的性能。边界框的回归为：
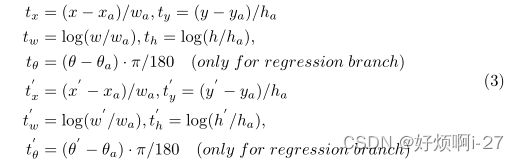
（x,y,w,h, θ）分别表示长方体的中心坐标、宽度、高度和角度。变量x，xa，x0分别用于地面真值框、锚框和预测框（同样用于y、w、h、θ）。多任务损失为：
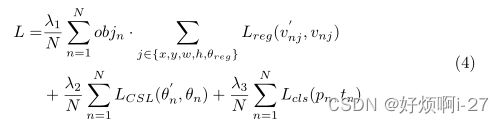
N是锚的数量，objn是一个二进制值（objn=1表前景，objn=0表背景， 背景无回归）， 表示预测偏移量，v∗j是地面真实目标向量， 分别表 示角度的标记和预测，tn是对象的标签，pn是有Sigmoid函数计算的 各种类的概率分布。超参数λ1、λ2、λ3控制权衡，默认设置{1,0.5,1}。 分类损失Lcls和LCSL是焦点损失或sigmoid交叉熵损失，取决于检测 器。回归损失Lreg使用的是L1损失。高斯函数形式表现出了最好的性能，当半径太小时，g（x）趋向于脉冲函数，相反，对所有可预测结果的区分变得更小。单探测器对半径更为敏感，推测得两级检测器中的实例级特征提取能力强于单级检测器的图像级，因此，两阶段检测方法可以区分两个接近角之间的差异。
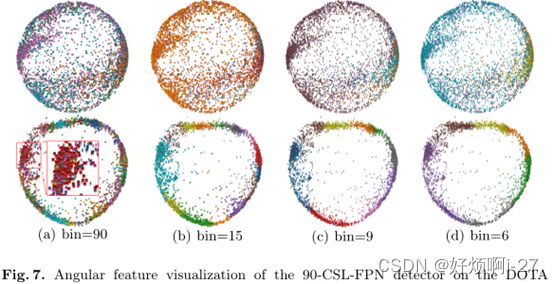从图7看出，Rol的特征分布是相对随机，一些角度的预测结果占据了绝大多数，对于高斯函数，特征分布时明显的环形结构，相邻角的特征彼此接近并具有一定的重叠，这种特性帮助基于CSL的检测器消除边界问题，并准确地获得对象的方向和尺度信息。
最后一篇是Rethinking rotated object detection with gaussian wasserstein distance loss. In ICML,2021（基于高斯Wassertein距离损失的旋转目标检测）
本文是提出的一种基于高斯Wassertein距离的回归损失作为解决边界不连续性及其与最终检测度量的不一致性的问题。旋转的边界框被转换为二维高斯分布，这使得能够通过高斯Wassertein距离（GWD）来近似不可微分的旋转IoU引起的损失，该距离可以通过梯度反向传播来有效学习。即使两个旋转边界框之间没有重叠，GWD仍然可以为学习提供信息，这通常是小对象检测的情况。同时GWD可以在不管边界框怎么定义的情况下，解决边界不连续性和正方形问题。
贡献：
（1）总结了旋转检测器的三个缺陷，即度量和损失之间的不一致性、边界不连续性和正方形问题，这是由于它们基于回归的角度预测性质；
（2）通过GWD对旋转边界框距离进行建模，通过将模型学习重新思考旋转目标检测与GWD损失与精度度量对齐来解决损失不一致性，改进模型；
（3）在不管旋转边界框怎么定义的情况下，基于GWD的损失可以解决边界不连续和类正方形问题。
边界框定义特定探测器有相关两种基于旋转边界框的角度参数化定义（OpenCV协议），左：OpenCV定义Doc；右：长边定义Dlc，注释θ∈[-90°，0°),前者表示边界框的hoc与x轴之间的锐角或直角；相反θ∈[-90°，90°)后者定义是边界框的长边hle与x轴之间的角度。两种参数化可以相互转换：
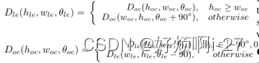
度量和联合损失交集（IoU）之间的不一致性会导致较小的训练损失不能保证较高的性
能，两个边界框的平滑L1损失是恒定的（主要来自角度差），但IoU将随着纵横比的变
化而急剧变化。与水平检测不同，两个旋转盒的IoU对于学习来说是不可区分的，可以
用GWD的可微损耗来代替硬IoU损耗。边界不连续通常指角度和边缘参数化引起的边
界处的急剧损失增加。由于角度的周期性（PoA）和边缘的可交换性（EoE），会出
现非常大的平滑L1损失。因此，模型必须以其他复杂的回归形式进行预测。
旋转物体检测器，其回归损失满足以下要求：（1）与IoU诱导的度量高度一致
（解决了类正方形物体问题）；（2）允许直接学习；（3）在角边界情况下平滑。
旋转边界框的GWD大多数基于IoU的损失可以被视为距离函数。提出一种基于GWD
的新回归损失。通过以下公式将旋转边界框（x，y，h，w，θ）转换为二维高斯分
布N（m，∑）：
Rn上两个概率测度μ和v之间的GWD的W表示为：
其中下一个在Rn*Rn的所有随机向量（X，Y）上运行X~μ和Y~v，
d:=W(N(m1,∑);N(m2,∑))，并可以写为：
又由
在交换的情况下（水平检测任务）∑1∑2=∑2∑1，可变为：
||||F是Frobenius范数
将GWD转换为类似于两个边界框之间的IoU的亲和度度量
，遵循检测文献中基于IoU的标准损失形式：
f(·)和τ的不同组合下的函数曲线，与平滑L1损耗相比，GWD可以测量两个非重叠边界框之间的距离（IoU=0）。旋转矩形由五个参数（x，y，w，h，θ）表示，在实验中，主要遵循Doc，回归方程如下：
多任务损失为：
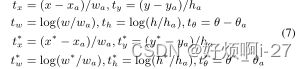
N表示锚的数量，objn是一个二进制值（前景objn=1，背景objn=0，背景无回归）。
Bn表示第n个预测边界框，gtn是第n个ground-truth。tn表示第n个对象的标号，pn
是通过sigmoid函数计算的各种类别的第n个概率分布。超参数λ1、λ2控制权衡，默
认设置为{2,1}。在计算边界位置的IoU之前，IoU Smooth L1 Loss需要确定预测框
是否在定义的范围内，否则，需要转换为与ground-truth相同的定义，需要作出额
外的判断才能解决所有问题。
总结
看完这几篇目标检测，发现检测比较难，现在准备转战检索了