Matlab 主成分分析与K均值聚类分析实验报告

Matlab 主成分分析与K均值聚类分析实验报告

提示：数据资源在本CSDN号的上传资料中直接领取

---

1 引言

数据：gyzb.mat（按顺序对应每一列）为：31个省市区的国有控股企业的主要指标（包括：总利润（亿元）、总资产贡献率（%）、资产负债率（%）、流动资产周转次数（次/年）、工业成本费用利用率（%）和人均主营收入（万元/人））。需要使用数据分析方法对该数据进行分析，试着得出一些分析总结。这里使用的分析方法为：主成分分析、K均值聚类分析。

---

2 算法原理

2.1 主成分分析的简介及算法原理

（1）简介：

主成分分析（Principal Component Analysis，PCA）， 是一种分析方法。首先是由K.皮尔森（Karl Pearson）对非随机变量引入的，尔后H.霍特林将此方法推广到随机向量的情形。信息的大小通常用离差平方和或方差来衡量。通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量，转换后的这组变量叫主成分。在实际中，为了全面分析问题，往往提出很多与此有关的变量（或因素），因为每个变量都在不同程度上反映这个问题的某些信息。

（2）PCA的算法原理：

将n维特征映射到k维上（k

（3）算法步骤：

【1】对原始数据进行标准化处理。

【2】计算样本的相关系数矩阵。

【3】计算相关系数矩阵的特征值和特征向量。

【4】计算主成分贡献率和累计贡献率。

【5】计算主成分载荷和主成分。

2.2 K均值聚类分析的简介及算法原理

（1）简介：

K均值聚类分析是将样本数据矩阵划分为K个类，使得所有类内对象与该类中心点之间的距离和最小。它属于聚类分析（非监督学习）一种分析方法。

（2）大致算法原理：

首先随机选择初始聚类中心，其中K是用户指定的参数（需要分成几类），然后将数据集中的每个点指派到最近的聚类中心，而指派到一个聚类中心的点就为一个簇（或类别）。然后再根据指派到簇的点，将每个簇的聚类中心更新为该簇所有点的平均值，重复指派和更新步骤，直到簇不发生变化，或者等价的，直到聚类中心不发生变化。

（3）大致算法步骤：

【1】随机地取K个点作为K个初始聚类中心。

【2】计算其它点到这个K个聚类中心的距离。

【3】如果某个点p1距离第n个聚类中心的距离更近（按最小距离准则），则该点p1属于第n个类别，并对其打标签。

【4】计算同一个类中，也就是相同标签的点向量的平均值，作为新的聚类中心。

【5】迭代至所有聚类中心都不变化为止，即算法结束。

（4）适用范围：

K均值适用于绝大多数的数据类型，并且思路不难且有效。但缺点是需要知道K的值，并且不能处理异形簇，比如环形簇、球形簇等。

---

3 实验结果与分析

3.1 主成分分析的实验结果与分析：

（1）实验思路:

gyzb.mat数据文件是一个每一列都是数据值的样本数据矩阵，列数多，且没有可供判断类别列也没有时间值等。列数多就暂不考虑多元回归分析，没有判断类别就暂不考虑各种判别分析方法，如（贝叶斯判决、神经网络判决、KNN等）。想到可选择对gyzb.mat数据文件进行K均值聚类分析，还有就是因为Matlab有pca()等内置函数，就开始实验了。

（2）实验步骤：

【1】先导入gyzb.mat数据文件，然后观察数据的大致情况；

【2】选择主成分分析；

【3】先在matlab脚本中写好大致的代码思路；

【4】再试着进行编写matlab代码，边写边测试边修改代码边回顾知识；

【5】试着对运行得出的结果及统计图进行分析。

【6】试着修改统计图。

【7】后来增加了基于主成分的K均值聚类分析。

（3）结果及分析：

（3.1）matlab代码1：

# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #

clc

disp('【1】主成分分析：')
% （1）导入样本数据
load('gyzb_data.mat');

% （2）使用标准化，对样本进行归一化处理, z为标准化后的数据，mu是原样本的均值，sigma是原样本的方差。
[z, mu, sigma] = zscore(gyzb_data);
disp('(1)原样本数据的均值：')
disp(mu)
disp('(2)原样本数据的方差：')
disp(sigma)
disp('(3)标准化后的数据：')
disp(z)

% （3）进行主成分分析
% coeff是n×m 数据矩阵 gyzb_data 的主成分系数矩阵，主成分系数也称为载荷。
% gyzb_data 的行对应于观测值，列对应于变量。系数矩阵是 m×m 矩阵。coeff 的每列包含一个主成分的系数，并且这些列按成分方差的降序排列。
% 默认情况下，pca 将数据中心化，并使用奇异值分解 (SVD) 算法。
% score 中返回主成分分数，在 latent 中返回主成分方差。主成分方差是 z 的协方差矩阵的特征值。
[coeff, score, latent] = pca(z);
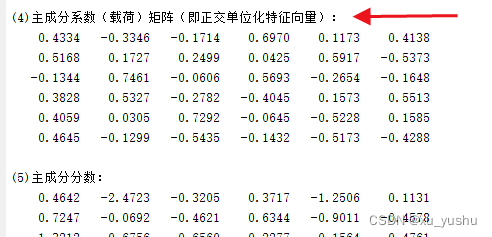
disp('(4)主成分系数（载荷）矩阵（即正交单位化特征向量）：')
disp(coeff)
disp('(5)主成分分数：')
disp(score)
disp('(6)主成分方差（即特征值）：')
disp(latent)

% （4）计算每一种主成分的贡献率
perContributionRate = 100*latent/sum(latent);
disp('(7)每一种主成分(每一列)的贡献率(单位为 %):')
disp(perContributionRate)

% （5）计算累积贡献率
cumContributionRate = cumsum(perContributionRate);
disp('(8)计算累积贡献率(单位为 %):')
disp(cumContributionRate)

% （6）这里绘制出前两个主成分得分的散点图
figure(1);
plot(score(:, 1), score(:, 2), 'o');
title('前两个主成分得分的散点图:')
xlabel('前第一列的主成分得分');
ylabel('前第二列的主成分得分');

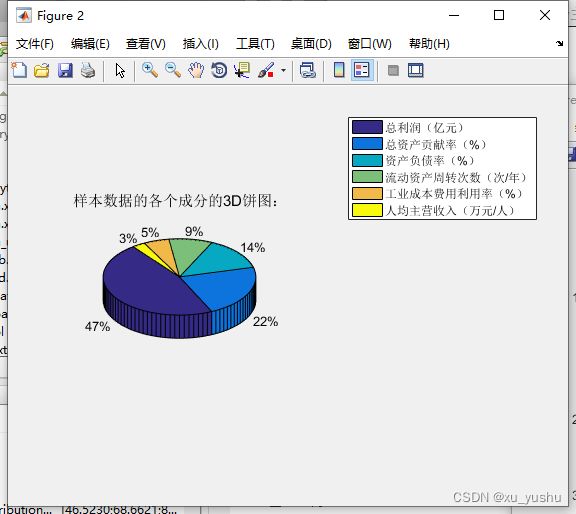
% （7）绘制出各个成分的3D饼图
figure(2);
pie3(perContributionRate);
title('样本数据的各个成分的3D饼图：')
legend('总利润（亿元）', '总资产贡献率（%）', '资产负债率（%）', '流动资产周转次数（次/年）', '工业成本费用利用率（%）', '人均主营收入（万元/人）');

% （8）利用主成分表达式，求主成分，并形成主成分矩阵Y，将样本数据降为3维
Y = gyzb_data*coeff(:,1:3);

% （9）开始基于主成分的K均值聚类分析：
disp('基于主成分的K均值聚类分析：')

% （10）选择初始聚类中心点。
startdata1 = Y([5, 15, 25],:);

% （11）获取聚类结果，index为聚类结果
[index, ctrs] = kmeans(Y, 3, 'start', startdata1);

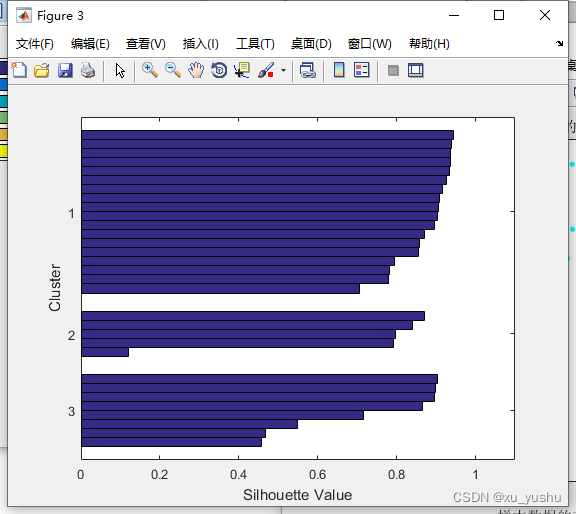
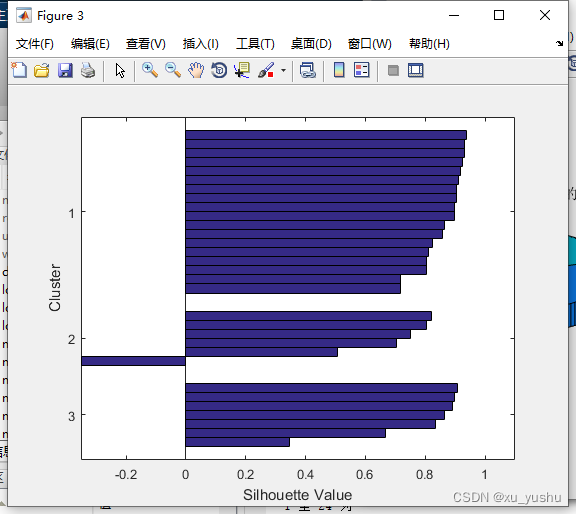
% （12）绘制出轮廓图，s1为轮廓向量，h1为图形句柄
figure(3)
[s1, h1] = silhouette(Y, index);

% （13）对聚类结果矩阵、轮廓值向量进行转置输出，（size(idx)、size(s)都为31行1列）
disp('(1)轮廓图的轮廓值向量：')
disp(s1')
disp('(2)使用K均值聚类后，样本数据的各行的聚类类别：')
disp(index')
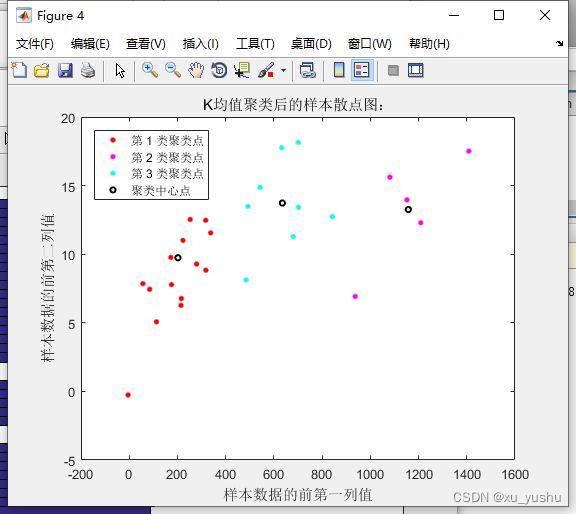
figure(4);
plot(Y(index==1,1),Y(index==1,2),'r.','MarkerSize',12)
hold on
plot(Y(index==2,1),Y(index==2,2),'m.','MarkerSize',12)
hold on
plot(Y(index==3,1),Y(index==3,2),'c.','MarkerSize',12)
hold on
plot(ctrs(:,1),ctrs(:,2),'ko','MarkerSize',4,'LineWidth',1.5)
legend('第 1 类聚类点','第 2 类聚类点','第 3 类聚类点','聚类中心点','Location','NW')
title('基于主成分的K均值聚类后的样本散点图：');
xlabel('主成分的前第一列值');
ylabel('主成分的前第二列值');

**# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #**

（3.2）结果截图及分析：

温馨提示：基于主成分的聚类分析的结果显示在后面！

分析：由上面的结果可知：标准化后的样本数据的前三列贡献率达到82.5654%，已经超过2/3以上，且这上列数据为’总利润（亿元）', ‘总资产贡献率（%）’, '资产负债率（%）‘的实际意义等，大致可以将这3个变量取代原来的6个变量，来实现降维。通过主成分系数（载荷）矩阵（即正交单位化特征向量矩阵）的前三列乘以样本数据矩阵。就能够形成新的近似样本的矩阵，它的规模从316降为313。（该矩阵不是原始样本数据的’总利润（亿元）’, ‘总资产贡献率（%）’, '资产负债率（%）'那3列,而是代表这31个省市区的国有控股工业企业的主要指标，即原始样本数据。）

3.2 K均值聚类分析的实验结果与分析：

（1）实验思路：

gyzb.mat数据文件是一个每一列都是数据值的样本数据矩阵，列数多，且没有可供判断类别列也没有时间值等。列数多就暂不考虑多元回归分析，没有判断类别就暂不考虑各种判别分析方法，如（贝叶斯判决、神经网络判决、KNN等）。想到可选择对gyzb.mat数据文件进行K均值聚类分析，还有就是因为Matlab有Kmeans()、silhouette()等内置函数，就开始实验了。

（2）实验步骤：

【1】先导入gyzb.mat数据文件，然后观察数据的大致情况；

【2】选择K均值聚类分析；

【3】先在matlab脚本中写好大致的代码思路；

【4】再试着进行编写matlab代码，边写边测试边修改代码边回顾知识；

【5】试着对运行得出的结果及统计图进行分析。

【6】试着修改统计图。

（3）结果及分析：

（3.1）matlab代码：

# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #
disp(' ')
disp('【2】K均值聚类分析：')
% （1）导入样本数据
% （2）选择初始凝聚点。
startdata = gyzb_data([5, 15, 25],:);
% （3）获取聚类结果，idx为聚类结果
[idx, ctrs] = kmeans(gyzb_data, 3, 'start', startdata);
% （4）绘制出轮廓图，s为轮廓向量，h为图形句柄
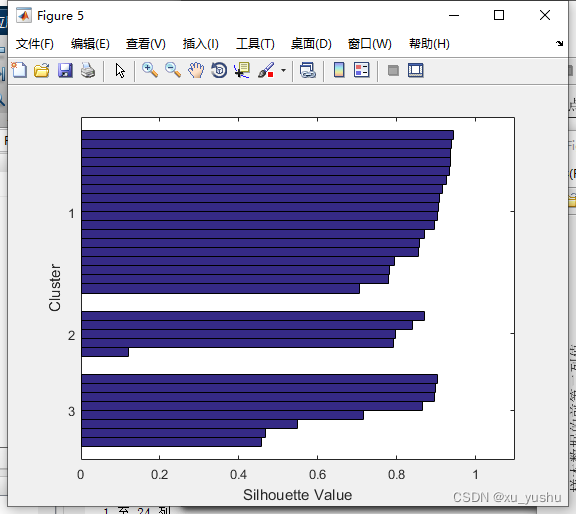
figure(3)
[s, h] = silhouette(gyzb_data, idx);
% （5）对聚类结果矩阵、轮廓值向量进行转置输出，（size(idx)、size(s)都为31行1列）
disp('(1)轮廓图的轮廓值向量：')
disp(s')
disp('(2)使用K均值聚类后，样本数据的各行的聚类类别：')
disp(idx')
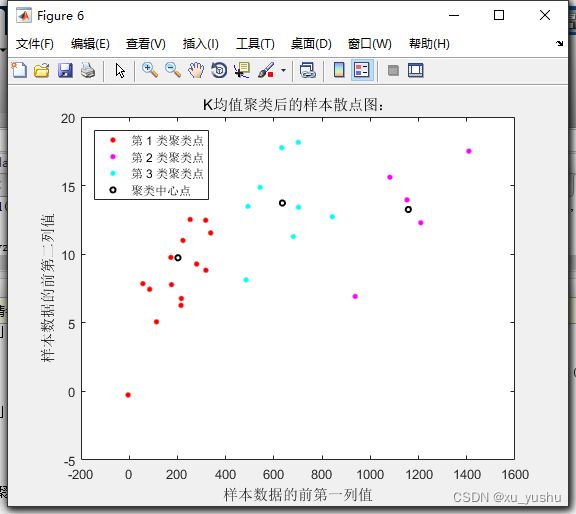
figure(4);
plot(gyzb_data(idx==1,1),gyzb_data(idx==1,2),'r.','MarkerSize',12)
hold on
plot(gyzb_data(idx==2,1),gyzb_data(idx==2,2),'m.','MarkerSize',12)
hold on
plot(gyzb_data(idx==3,1),gyzb_data(idx==3,2),'c.','MarkerSize',12)
hold on
plot(ctrs(:,1),ctrs(:,2),'ko','MarkerSize',4,'LineWidth',1.5)
legend('第 1 类聚类点','第 2 类聚类点','第 3 类聚类点','聚类中心点','Location','NW')
title('K均值聚类后的样本散点图：')
xlabel('样本数据的前第一列值');
ylabel('样本数据的前第二列值');
# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #

（3.2）结果截图及分析：

（3.2.1）聚类结果文本显示：

【2】K均值聚类分析：

(1)轮廓图的轮廓值向量：

1 至 14 列

 0.1194  0.9029  0.9376  0.9266  0.9382  0.9449  0.8985  0.8650  0.7922  0.4571  0.7159  0.7824  0.9051  0.8947

15 至 28 列

 0.8702  0.8701  0.8966  0.8578  0.7976  0.9327  0.9078  0.7069  0.4671  0.7803  0.7943  0.8544  0.8397  0.9370

29 至 31 列

 0.9158  0.9030  0.5497

(2)使用K均值聚类后，样本数据的各行的聚类类别：

1 至 24 列2

  2   3   1   1   1   1   3   3   2   3   3   1   1   1   2   1   3   1   2   1   1   1   3   1

25 至 31 列

  1   1   2   1   1   1   3

分析：这里做过修改多次修改初始聚类中心的测试，由于篇幅过于赘余，便省掉了一些数据，测试后：聚类效果几乎相似。可以推断：初始的聚类中心的不同，对聚类结果没有很大的影响，而对迭代次数有明显的影响。数据的输入顺序不同，同样会影响迭代次数，而对聚类结果没有太大的影响。

（3.2.2）：聚类结果轮廓图显示：

【统计图1】

（3.2.3）聚类结果散点图显示：

【统计图2】

结果分析：根据（3.2.1）、【统计图1】、【统计图2】等，可见在K=3的情况下，即聚成3种类别的情况下，样本点的簇在（类别）分配结果值算是不错的。就是说：根据31各省市区的国有控股工业企业的主要指标，可以将这31个企业分配成3种类别的企业。

但是也得考虑k-均值算法收敛到了局部最小值，而非全局最小值。因而使用不同的K的K均值算法的聚类结果不是都是那么可观、分明的。

（3.3）基于主成分的K均值聚类分析与K均值聚类分析的结果比较：

（3.3.1）聚类结果的结果比较：

* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *

【1】基于主成分的K均值聚类分析：

(1)轮廓图的轮廓值向量：

 1 至 14 列

  0.5077  0.8351  0.9309  0.9049  0.9326  0.9378  0.8991  0.8651  0.7025  -0.3507  0.8915  0.8044  0.8101  0.8043

 15 至 28 列

  0.8204  0.9112  0.9076  0.8575  0.8026  0.9053  0.9193  0.7174  0.3470  0.8641  0.7180  0.8240  0.7506  0.9254

 29 至 31 列

  0.8967  0.8982  0.6657

(2)使用K均值聚类后，样本数据的各行的聚类类别：

 1 至 24 列

   2   3   1   1   1   1   3   3   2   **2**   3   1   1   1   2   1   3   1   2   1   1   1   3   1

 25 至 31 列

   1   1   2   1   1   1   3

* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *

【2】K均值聚类分析：

(1)轮廓图的轮廓值向量：

 1 至 14 列

  0.1194  0.9029  0.9376  0.9266  0.9382  0.9449  0.8985  0.8650  0.7922   0.4571  0.7159  0.7824  0.9051  0.8947

 15 至 28 列

  0.8702  0.8701  0.8966  0.8578  0.7976  0.9327  0.9078  0.7069  0.4671  0.7803  0.7943  0.8544  0.8397  0.9370

 29 至 31 列

  0.9158  0.9030  0.5497

(2)使用K均值聚类后，样本数据的各行的聚类类别：

 1 至 24 列2

   2   3   1   1   1   1   3   3   2   **3**   3   1   1   1   2   1   3   1   2   1   1   1   3   1

 25 至 31 列

   1   1   2   1   1   1   3

* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *

（3.3.2）聚类轮廓图的结果比较

【1】基于主成分的K均值聚类分析轮廓图：

【2】K均值聚类分析轮廓图：

（3.3.3）聚类效果散点图：

【1】基于主成分的K均值聚类分析：

【2】K均值聚类分析：

分析：基于主成分的K均值聚类分析与K均值聚类分析的聚类结果只有一项（即第10行数据）不一致，其两者对应的轮廓图几乎是近似的，其对应聚类效果散点图虽然由于坐标轴的不对应等而产生的显示效果，但其聚类效果几乎是近似且可观。可见基于主成分的K均值聚类分析与原数据的K均值聚类分析的聚类结果可以说是近似，这也间接地说明前面进行的主成分分析，然后进行数据降维的处理算是合理的。

4 总结

主成分分析对于处理“31各省市区的国有控股工业企业的主要指标”的数据矩阵的降维来说是很可靠的。在做主成分分析时，若是面对每列数值差异性过大的样本数据可考虑进行标准化处理，然后再进行主成分分析等降维处理。在K均值聚类分析中，初始的聚类中心的不同，对聚类结果没有很大的影响，而对迭代次数有明显的影响。数据的输入顺序不同，同样会影响迭代次数，而对聚类结果没有太大的影响。而对K的取值，对聚类结果的影响却是很大的，这是由于研究者或测试者的主观因素，K的取值可以说还是得吃经验、需要对数据有点敏感的。聚类结果得出的类别，还可以在类别内部进行分析。

---

参考文献

《MATLAB数据分析教程》， 由伟、刘亚秀， 清华大学出版社

《MATLAB数据分析方法》， 李柏年、吴礼斌，张孔生，丁华， 机械工业出版社

《MATLAB数据分析与挖掘实战》， 张良均等， 机械工业出版社， 2015.06.01