信息抽取（五）实体命名识别之嵌套实体识别哪家强，我做了一个简单的对比实验

---

嵌套实体识别

1. 嵌套实体识别是实体命名识别中一个子问题，何为嵌套实体即“北京天安门”中“北京”是地点实体，“北京天安门”同样也是地点实体，两者存在嵌套关系。使用CRF等传统标注方法无法对嵌套实体进行区分，因此存在一定的局限性。
2. 目前流行构建实体矩阵，即用一个矩阵$W_{tse}(type,len,len)$来代表语料中的所有实体及其类型，其中任一元素$N_{t,e,s}$表示类行为$t$，起点为$s$，结尾为$e$的实体。通过这样的标注方式我们可以对任何嵌套实体进行标注，从而解决训练和解码的问题。
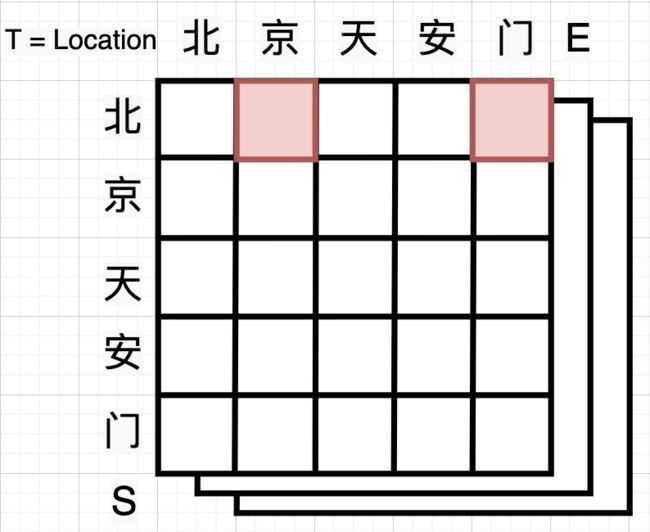
3. 本文笔者将对比目前接触到的部分实体矩阵的构建方法在CMeEE数据集（医学NER，有一定嵌套实体）上的表现。

实体矩阵构建框架

1. 为了方便后续对比说明，这里定义几个同一的变量与符号，上文中$N_{tes}$表示类行为$t$，起点为$s$，结尾为$e$的实体。在本实验中，我们均适用bert-base-chinese作为encoder，$h_i$表示最后一层隐藏层中第$i$个token的embedding，则$h_s$和$h_e$分别表示经过encoder之后实体Start和End token的embedding，则我们有公式$N_{t,e,s}=p(h_s,h_e,t)$，其中$p(x)$就表示我们所需要对比的实体矩阵构建头（姑且这么称呼）。
2. 在对比实验中，除了不同实体矩阵构建头对应的batch_size，learning_rate不同，所使用的encoder、损失函数、评估方式以及训练轮次均保持一致。
3. 本文选取了GlobalPointer、TPLinker（Muti-head selection)、Tencent Muti-head、Deep Biaffine（双仿射）共四种实体矩阵构建方法进行比较。

---

方法比较

GlobalPointer

1. GlobalPointer出自苏神的博客GlobalPointer：用统一的方式处理嵌套和非嵌套NER
2. 计算公式：$p(h_s,h_e,t)=q_{s,t}^T{k}_{e,t}$，其中$q_{s,t}=W_{s,t}{h}_s+b_{s,t}$，$k_{e,t}=W_{e,t}{h}_e+b_{e,t}$
3. 其核心思想为类似attention的打分机制，将多种个实体类型的识别视为Muti-head机制，将每一个head视为一种实体类型识别任务，最后利用attention的score(QK)作为最后的打分。
4. 为了考虑到Start和end之间距离的关键信息，作者在此基础上引入了旋转式位置编码（RoPE），在其文中显示引入位置信息能给结果带来极大提升，符合预期先验。

class GlobalPointer(Module):
    """全局指针模块
    将序列的每个(start, end)作为整体来进行判断
    """
    def __init__(self, heads, head_size,hidden_size,RoPE=True):
        super(GlobalPointer, self).__init__()
        self.heads = heads
        self.head_size = head_size
        self.RoPE = RoPE
        self.dense = nn.Linear(hidden_size,self.head_size * self.heads * 2)

    def forward(self, inputs, mask=None):
        inputs = self.dense(inputs)
        inputs = torch.split(inputs, self.head_size * 2 , dim=-1)
        inputs = torch.stack(inputs, dim=-2)
        qw, kw = inputs[..., :self.head_size], inputs[..., self.head_size:]
        # RoPE编码
        if self.RoPE:
            pos = SinusoidalPositionEmbedding(self.head_size, 'zero')(inputs)
            cos_pos = pos[..., None, 1::2].repeat(1,1,1,2)
            sin_pos = pos[..., None, ::2].repeat(1,1,1,2)
            qw2 = torch.stack([-qw[..., 1::2], qw[..., ::2]], 4)
            qw2 = torch.reshape(qw2, qw.shape)
            qw = qw * cos_pos + qw2 * sin_pos
            kw2 = torch.stack([-kw[..., 1::2], kw[..., ::2]], 4)
            kw2 = torch.reshape(kw2, kw.shape)
            kw = kw * cos_pos + kw2 * sin_pos
        # 计算内积
        logits = torch.einsum('bmhd , bnhd -> bhmn', qw, kw)
        # 排除padding,排除下三角
        logits = add_mask_tril(logits,mask)
        return logits / self.head_size ** 0.5

TPLinker

1. TPLinker出自论文TPLinker: Single-stage Joint Extraction of Entities and Relations
   Through Token Pair Linking，其本为解决实体关系抽取设计，其原型为Joint entity recognition and relation extraction as a multi-head selection problem论文中的Muti-head selection机制。此处选取其中用于识别实体部分的机制，作为对比对象。
2. 计算公式：$p(h_s,h_e,t)=W_t\cdot h_{s,e}+b_t$，其中$h_{s,e}=tanh(W_h\cdot [h_s;h_e]+b_h)$
3. 与GlobalPointer不同的是，GlobalPointer是乘性的，而Muti-head是加性的。对于这两种机制的不同，笔者在之前的文章信息抽取（四）中做过简单的对比。但对于这两种机制，谁的效果更好，我们无法仅通过理论进行分析，因此需要做相应的对比实验，从结果进行倒推。但是在实际Implement的过程中，笔者发现加性比乘性占用更多的内存，但是与GlobalPointer中不同的是，加性仍然能实现快速并行，需要在计算设计上加入一些技巧。

class MutiHeadSelection(Module):

    def __init__(self,hidden_size,c_size,abPosition = False,rePosition=False, maxlen=None,max_relative=None):
        super(MutiHeadSelection, self).__init__()
        self.hidden_size = hidden_size
        self.c_size = c_size
        self.abPosition = abPosition
        self.rePosition = rePosition
        self.Wh = nn.Linear(hidden_size * 2,self.hidden_size)
        self.Wo = nn.Linear(self.hidden_size,self.c_size)
        if self.rePosition:
            self.relative_positions_encoding = relative_position_encoding(max_length=maxlen,
            						depth= 2 * hidden_size,max_relative_position=max_relative)
                                                                  
    def forward(self, inputs, mask=None):
        input_length = inputs.shape[1]
        batch_size = inputs.shape[0]
        if self.abPosition:
            # 由于为加性拼接，我们无法使用RoPE,因此这里直接使用绝对位置编码
            inputs = SinusoidalPositionEmbedding(self.hidden_size, 'add')(inputs)
        x1 = torch.unsqueeze(inputs, 1)
        x2 = torch.unsqueeze(inputs, 2)
        x1 = x1.repeat(1, input_length, 1, 1)
        x2 = x2.repeat(1, 1, input_length, 1)
        concat_x = torch.cat([x2, x1], dim=-1)
        # 与TPLinker原论文中不同的是，通过重复+拼接的方法构建的矩阵能满足并行计算的要求。
        if self.rePosition:
        	# 如果使用相对位置编码，我们则直接在矩阵上实现相加
            relations_keys = self.relative_positions_encoding[:input_length, :input_length, :].to(inputs.device)
            concat_x += relations_keys
        hij = torch.tanh(self.Wh(concat_x))
        logits = self.Wo(hij)
        logits = logits.permute(0,3,1,2)
        logits = add_mask_tril(logits, mask)
        return logits

Tencent Muti-head

1. 论文EMPIRICAL ANALYSIS OF UNLABELED ENTITY PROBLEM IN NAMED ENTITY RECOGNITION 提出了一种基于片段标注解决实体数据标注缺失的训练方法——负采用，并在部分数据集上达到了SOTA。关注其实体矩阵构建模块，相当于Muti-head的升级版，因此我把它叫做Tencent Muti-head。
2. 计算公式：$p(h_s,h_e,t)=U\cdot tanh(V{s}_{s,e})$，其中$s_{s,e}=[h_s;h_e;h_s-h_e;h_s\cdot h_e]$
3. 与TPLinker相比，Tencent Muti-head在加性的基础上加入了更多信息交互元素：$h_s-h_e，h_s\cdot h_e$（作差与点乘），但同时也提高了内存的占用量。

class TxMutihead(Module):

    def __init__(self,hidden_size,c_size,abPosition = False,rePosition=False, maxlen=None,max_relative=None):
        super(TxMutihead, self).__init__()
        self.hidden_size = hidden_size
        self.c_size = c_size
        self.abPosition = abPosition
        self.rePosition = rePosition
        self.Wh = nn.Linear(hidden_size * 4, self.hidden_size)
        self.Wo = nn.Linear(self.hidden_size,self.c_size)
        if self.rePosition:
            self.relative_positions_encoding = relative_position_encoding(max_length=maxlen,
            						depth= 4 * hidden_size,max_relative_position=max_relative)
            
    def forward(self, inputs, mask=None):
        input_length = inputs.shape[1]
        batch_size = inputs.shape[0]
        if self.abPosition:
            # 由于为加性拼接，我们无法使用RoPE,因此这里直接使用绝对位置编码
            inputs = SinusoidalPositionEmbedding(self.hidden_size, 'add')(inputs)
        x1 = torch.unsqueeze(inputs, 1)
        x2 = torch.unsqueeze(inputs, 2)
        x1 = x1.repeat(1, input_length, 1, 1)
        x2 = x2.repeat(1, 1, input_length, 1)
        concat_x = torch.cat([x2, x1,x2-x1,x2.mul(x1)], dim=-1)
        if self.rePosition:
            relations_keys = self.relative_positions_encoding[:input_length, :input_length, :].to(inputs.device)
            concat_x += relations_keys
        hij = torch.tanh(self.Wh(concat_x))
        logits = self.Wo(hij)
        logits = logits.permute(0,3,1,2)
        logits = add_mask_tril(logits, mask)
        return logits

Deep Biaffine

1. 此处使用的双仿射结构出自论文Named Entity Recognition as Dependency Parsing，原文用于识别实体依存关系，因此也可以直接用于实体命名识别。
2. 计算公式：$p(h_s,h_e,t)=h_s^T{U}_t{h}_e+W_t[h_s;h_e]+b_t$
3. 简单来说双仿射分别对对s为头e为尾的实体类别后验概率建模 + 对s或e为尾的实体类别的后验概率分别建模 + 对实体类别t的先验概率建模。
4. 不难看出Deep Biaffine是加性与乘性的结合，更详细的解读可以参考信息抽取（四）
5. 在笔者复现的关系抽取任务中，双仿射确实带来的一定提升，但这种建模思路在实体识别中是否有效还有待验证。

class Biaffine(Module):

    def __init__(self, in_size, out_size, Position = False):
        super(Biaffine, self).__init__()
        self.out_size = out_size
        self.weight1 = Parameter(torch.Tensor(in_size, out_size, in_size))
        self.weight2 = Parameter(torch.Tensor(2 * in_size + 1, out_size))
        self.Position = Position
        self.reset_parameters()
    
    def reset_parameters(self):
        torch.nn.init.kaiming_uniform_(self.weight1,a=math.sqrt(5))
        torch.nn.init.kaiming_uniform_(self.weight2,a=math.sqrt(5))
    
    def forward(self, inputs, mask = None):
        input_length = inputs.shape[1]
        hidden_size = inputs.shape[-1]
        if self.Position:
            #引入绝对位置编码，在矩阵乘法时可以转化为相对位置信息
            inputs = SinusoidalPositionEmbedding(hidden_size, 'add')(inputs)
        x1 = torch.unsqueeze(inputs, 1)
        x2 = torch.unsqueeze(inputs, 2)
        x1 = x1.repeat(1, input_length, 1, 1)
        x2 = x2.repeat(1, 1, input_length, 1)
        concat_x = torch.cat([x2, x1], dim=-1)
        concat_x = torch.cat([concat_x, torch.ones_like(concat_x[..., :1])],dim=-1)
        # bxi,oij,byj->boxy
        logits_1 = torch.einsum('bxi,ioj,byj -> bxyo', inputs, self.weight1, inputs)
        logits_2 = torch.einsum('bijy,yo -> bijo', concat_x, self.weight2)
        logits = logits_1 + logits_2
        logits = logits.permute(0,3,1,2)
        logits = add_mask_tril(logits, mask)
        return logits

---

代码开源，各种实体矩阵构建方法都写成了类，方便大家复现或直接调用 https://github.com/zhengyanzhao1997/NLP-model/tree/main/model/model/Torch_model/ExtractionEntities

---

实验结果

1. GPU: P40 24G (x1)
2. 为了把各方法的内存占用情况考虑在内，本次对比实验全都在一张P40 24G的GPU上进行，并把Batch_size开到最大，其中仅GlobalPointer可以达到16，而Tencent Muti-head由于其构建了一个超大矩阵$(batchsize,maxlen,manlen,4\ast hiddensize)$占用内存较大，因此batch_size只能达到4，可以看出GlobalPointer的性能优势。
3. 由于注册的原因，这里只比较了各方法在训练过程中在验证集上的最好表现。

Method	Position	Batch_size	learning_rate	CMeEE${}_{train}$/F1%	CMeEE${}_{dev}$/F1%
GlobalPointer	RoPE	16	2e-5	73.23	64.64
TPLinker	\	8	1e-5	80.57	62.69
TPLinker	Pos${}_{ab}$	8	1e-5	83.21	63.10
TPLinker	Pos${}_{re}$	8	1e-5	76.63	64.32${}_{(64.99)}$
Tencent Muti-head	\	4	1e-5	83.50	63.74
Tencent Muti-head	Pos${}_{ab}$	4	1e-5	76.32	64.18
Tencent Muti-head	Pos${}_{re}$	4	1e-5	77.37	64.69
Tencent Muti-head	Pos${}_{re}$	16${}_{4卡}$	2e-5	68.81	64.83
Deep Biaffine	\	8	1e-5	78.27	62.85
Deep Biaffine	Pos${}_{ab}$	8	1e-5	77.52	62.66

---

总结

1. GlobalPointer作为乘性方法，在空间内存占用上明显优于其他方法，并且训练速度较快，能达到一个具有竞争力的效果。
2. TPLinker 和 Tencent Muti-head作为加性方法，在优化过程中均表现出 相对位置编码 > 绝对位置编码 > 不加入位置编码 的特征。这意味着在通过构建实体矩阵进行实体命名识别时位置信息具有绝对重要的优势，且直接引入相对位置信息较优。
3. 在绝对位置编码和不加入位置编码的测试中Tencent Muti-head的效果明显优于TPLinker而两者均差于GlobalPointer，但在引入相对位置信息后Tencent Muti-head略微超越了GlobalPointer，而TPLinker提点显著，作为Tencent Muti-head的原型在最高得分上甚至可能有更好的表现。
4. Biaffine双仿射表现不佳，意味着这种建模思路不适合用于实体命名识别。
5. 在计算资源有限的情况下GlobalPointer是最优的baseline选择，如果拥有足够的计算资源且对训练、推理时间的要求较为宽松，尝试使用TPLinker/Tencent Muti-head + 相对位置编码或许能取得更好的效果。

---

参考资料

1. 苏剑林. (May. 01, 2021). 《GlobalPointer：用统一的方式处理嵌套和非嵌套NER 》[Blog post]. Retrieved from https://kexue.fm/archives/8373
2. TPLinker: Single-stage Joint Extraction of Entities and Relations Through Token Pair Linking
3. EMPIRICAL ANALYSIS OF UNLABELED ENTITY PROBLEM IN NAMED ENTITY RECOGNITION
4. Named Entity Recognition as Dependency Parsing