NNDL 作业5 卷积

目录

作业1

编程实现

生成原图像：

1. 图1使用卷积核​编辑，输出特征图

2. 图1使用卷积核​编辑，输出特征图

3. 图2使用卷积核​编辑，输出特征图

4. 图2使用卷积核​编辑，输出特征图 

5. 图3使用卷积核​编辑，​编辑，​编辑 ，输出特征图 

作业2

一、概念

卷积：

卷积核

步长

特征图

特征选择

填充

感受野

二、探究不同卷积核的作用

三、编程实现

1.实现灰度图的边缘检测、锐化、模糊。

2.调整卷积核参数，测试并总结。

3.使用不同尺寸图片，测试并总结。

总结：

参考：

---

---

作业1

编程实现

1. 图1使用卷积核，输出特征图

2. 图1使用卷积核，输出特征图

3. 图2使用卷积核，输出特征图

4. 图2使用卷积核，输出特征图 

5. 图3使用卷积核，， ，输出特征图 

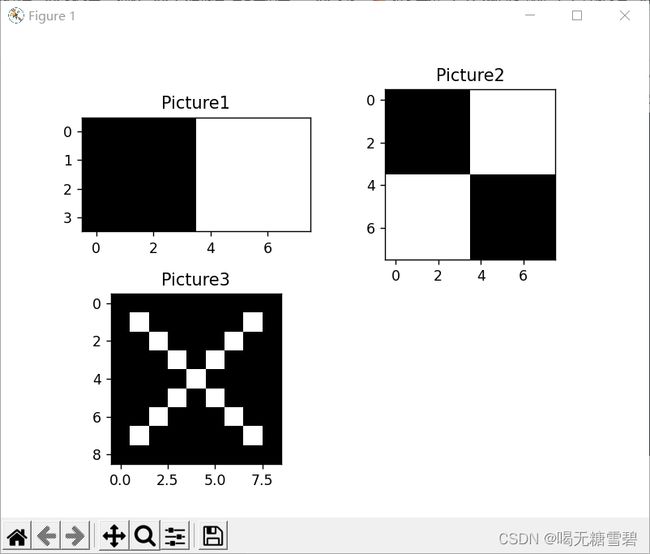
生成原图像：

import matplotlib.pyplot as plt
import torch
import numpy as np

# 生成图1，图2.图3
p1 = np.array([[0, 0, 0, 0, 255, 255, 255, 255],
               [0, 0, 0, 0, 255, 255, 255, 255],
               [0, 0, 0, 0, 255, 255, 255, 255],
               [0, 0, 0, 0, 255, 255, 255, 255]], dtype='float32')
p2 = np.array([[0, 0, 0, 0, 255, 255, 255, 255],
               [0, 0, 0, 0, 255, 255, 255, 255],
               [0, 0, 0, 0, 255, 255, 255, 255],
               [0, 0, 0, 0, 255, 255, 255, 255],
               [255, 255, 255, 255, 0, 0, 0, 0],
               [255, 255, 255, 255, 0, 0, 0, 0],
               [255, 255, 255, 255, 0, 0, 0, 0],
               [255, 255, 255, 255, 0, 0, 0, 0]], dtype='float32')
# 偷个懒，手打太多了
p3 = np.zeros((9, 9))
for i in range(1, 5):
    p3[i, i] = 255
    p3[i, 8-i] = 255
    p3[8-i, i] = 255
    p3[8-i, 8-i] = 255
# 显示题目已给的图像
plt.figure(1)
plt.subplot(2,2,1)
plt.title('Picture1')
plt.imshow(p1,cmap='gray')
plt.subplot(2,2,2)
plt.title('Picture2')
plt.imshow(p2,cmap='gray')
plt.subplot(2,2,3)
plt.title('Picture3')
plt.imshow(p3,cmap='gray')
# plt.show()

运行结果：

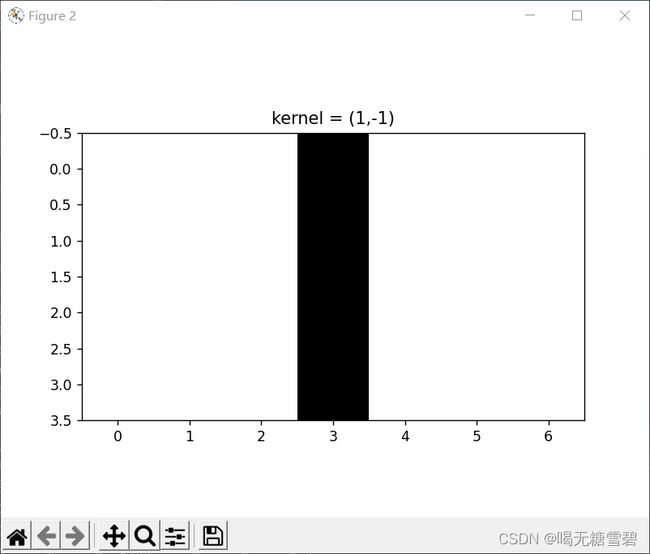
1. 图1使用卷积核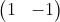，输出特征图

import matplotlib.pyplot as plt
import torch
import numpy as np

def cov2(picture,kernel,strde):
    # picture 为原图像，kernel 为卷积核，strde 为步长
    # x,y为矩阵的行列数
    x1, y1 = picture.shape
    x2, y2 = kernel.shape
    # x_count,y_count是计算在行列上卷积核与原图像的乘积次数,也是卷积后矩阵的行列数
    x3 = int((x1-x2)/strde+1)
    y3 = int((y1-y2)/strde+1)
    # 卷积后生成的新矩阵arr
    arr = np.zeros((x3,y3))
    # 先行后列进行卷积
    for i in range(0,y3):
        for j in range(0,x3):
            s = 0
            for m in range(0,x2):
                for n in range(0,y2):
                    s = s + picture[m+j*strde][n+i*strde]*kernel[m][n]
            arr[j][i] = s
    return arr
# 问题1
kernel1 = np.array([[1,-1]])   # 注意二维矩阵要用两个中括号
t1 = cov2(p1,kernel1,1)
print('图1使用卷积核(1,-1)后：')
print(t1)
plt.figure(2)
plt.title('kernel = (1,-1)')
plt.imshow(t1,cmap='gray')
# plt.show()

运行结果：

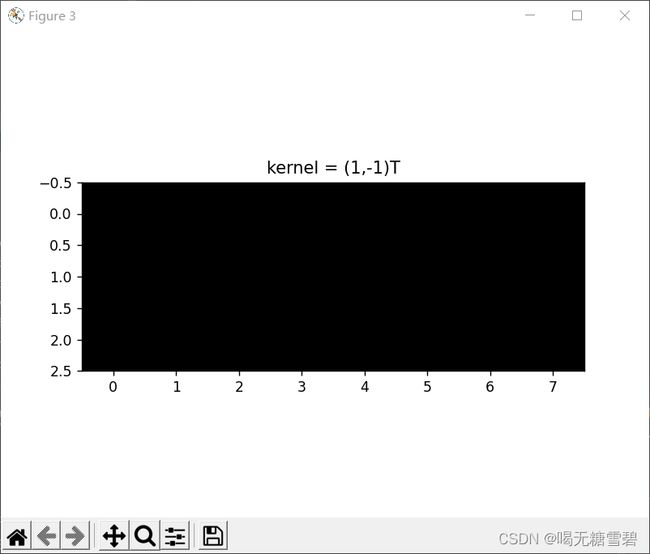
2. 图1使用卷积核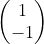，输出特征图

# 问题2
kernel2 = np.array(([[1],[-1]]))
t2 = cov2(p1,kernel2,1)
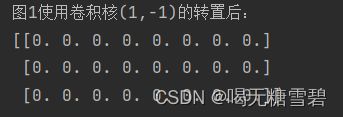
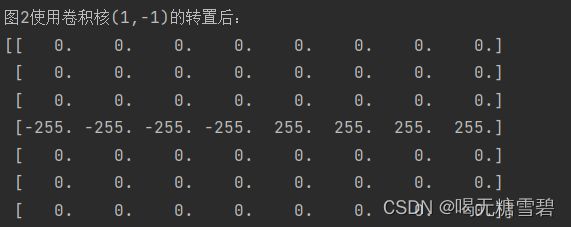
print('图1使用卷积核(1,-1)的转置后：')
print(t2)
plt.figure(3)
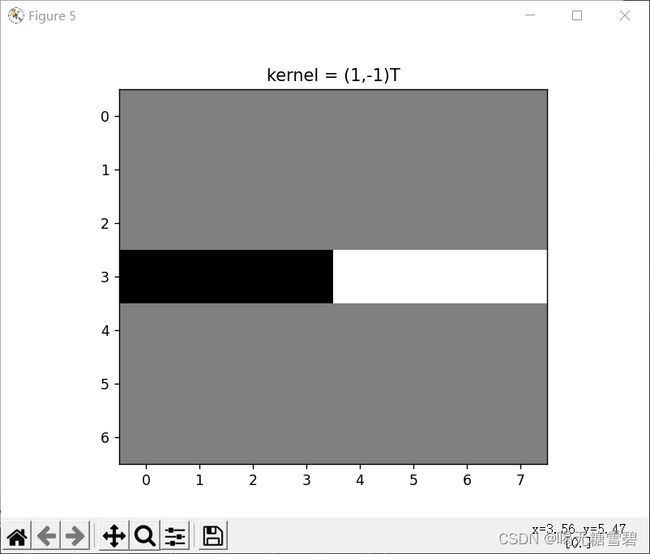
plt.title('kernel = (1,-1)T')
plt.imshow(t2,cmap='gray')
# plt.show()

运行结果：

 

3. 图2使用卷积核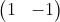，输出特征图

# 问题3
kernel3 = np.array([[1,-1]])   # 注意二维矩阵要用两个中括号
t3 = cov2(p2,kernel3,1)
print('图2使用卷积核(1,-1)后：')
print(t3)
plt.figure(4)
plt.title('kernel = (1,-1)')
plt.imshow(t3,cmap='gray')
plt.show()

运行结果：

 

4. 图2使用卷积核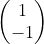，输出特征图 

# 问题4
kernel4 = np.array([[1,],[-1]])   # 注意二维矩阵要用两个中括号
t4 = cov2(p2,kernel4,1)
print('图2使用卷积核(1,-1)的转置后：')
print(t4)
plt.figure(5)
plt.title('kernel = (1,-1)T')
plt.imshow(t4,cmap='gray')
plt.show()

运行结果：

5. 图3使用卷积核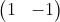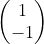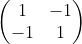，， ，输出特征图 

# 问题5
kernel5_1 = np.array([[1,-1]])   # 注意二维矩阵要用两个中括号
kernel5_2= np.array([[1],[-1]])
kernel5_3 = np.array([[1,-1],[-1,1]])

t5_1 = cov2(p3,kernel5_1,1)
t5_2 = cov2(p3,kernel5_2,1)
t5_3 = cov2(p3,kernel5_3,1)

print('图3使用卷积核(1,-1)后：')
print(t5_1)

print('图3使用卷积核(1,-1)的转置后：')
print(t5_2)

print('图3使用第三个卷积核后：')
print(t5_3)

plt.figure(6)
plt.subplot(2,2,1)
plt.title('kernel = (1,-1)')
plt.imshow(t5_1,cmap='gray')

plt.subplot(2,2,2)
plt.title('kernel = (1,-1)T')
plt.imshow(t5_2,cmap='gray')

plt.subplot(2,2,3)
plt.imshow(t5_3,cmap='gray')

plt.show()

运行结果：

 

 

作业2

一、概念

卷积：

教科书上一般定义函数 ​的卷积​如下：

​并且也解释了，先对g函数进行翻转，相当于在数轴上把g函数从右边褶到左边去，也就是卷积的“卷”的由来。

然后再把g函数平移到n，在这个位置对两个函数的对应点相乘，然后相加，这个过程是卷积的“积”的过程。

上图片直接感受下：

一维卷积：

 注意相乘的顺序是相反的，这是卷积的定义决定的。同时，在深度学习里为了方便，我们省去了翻转的步骤，直接对位相乘，这种叫做“互相关”，但在深度学习里也称之为卷积，而且一般用的卷积都是互相关。

二维卷积：

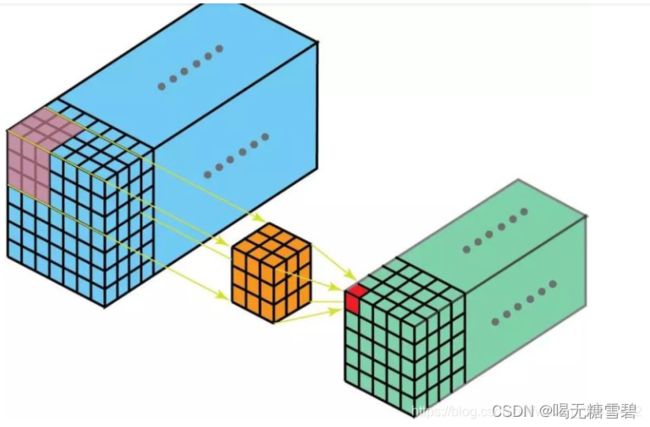
 三维卷积：

 以上图片分别来自于：

一维卷积

二维卷积

三维卷积

卷积核

卷积核就是图像处理时，给定输入图像，输入图像中一个小区域中像素加权平均后成为输出图像中的每个对应像素，其中权值由一个函数定义，这个函数称为卷积核。又称滤波器。可以看作对某个局部的加权求和；它是对应局部感知，它的原理是在观察某个物体时我们既不能观察每个像素也不能一次观察整体，而是先从局部开始认识，这就对应了卷积。,通俗的来说就是我们之前学过的加权求和的权值，通过这些权值计算出新的图像和矩阵。

步长

即卷积核进行一次卷积后，横向移动的步长和纵向移动的步长。

特征图

在我看来特征图就是原图像通过滤波器也就是与卷积核完成卷积后新生成的图像，因为卷积核具有对特征提取的作用，故此新生成的图像具有原图像的某些特征，因此成为特征图

特征选择

以我的认知来看特征选择就是将想找出的特征放在卷积核里然后通过卷积的方法在原图像中进行寻找，这样就能找到所求特征在原图中是否存在以及存在的个数、位置等

上图：

图片来自于：卷积神经网络工作原理的直观理解

填充

我们通过上面的几张图片也会发现，在进行完卷积后生成的矩阵的大小与原矩阵是不一样的，这是因为卷积核没法扩展到边缘区域以外,所以输入图像的边缘被“修剪”掉了。这就导致我们丢失了一部分边缘的信息。

Padding就是针对这个问题提出的一个解决方案：它会用额外的“假”像素填充边缘（值一般为0），这样，当卷积核扫描输入数据时，它能延伸到边缘以外的伪像素，从而使输出和输入大小相同。

如下图为一个卷积核为3×3、有padding、Stride为1时的卷积过程：

图中边缘虚线部分就是我们添加的“假”像素

感受野

• 感受野(receptive field)这一概念来自于生物神经科学，是指感觉系统中的任一神经元，其所受到的感受器神经元的支配范围。感受器神经元就是指接收感觉信号的最初级神经元
• 在卷积神经网络中，感受野（Receptive Field）的定义是卷积神经网络每一层输出的特征图（feature map）上的像素点在输入图片上映射的区域大小。

  

 图片来自于：

什么是感受野

二、探究不同卷积核的作用

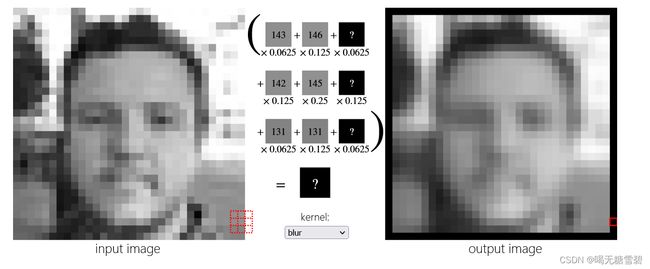
推荐下老师推荐的网站：Image Kernels

这里面可以直观感受到不同卷积核的作用。（试用了一下，深切感受到了先辈种树，后辈成荫的快乐，感谢做网站的大佬。

例：

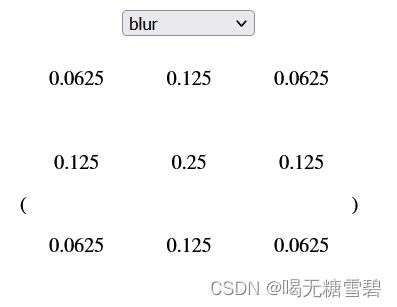
1.模糊

 

2.锐化

 

三、编程实现

• 实现灰度图的边缘检测、锐化、模糊。（必做）
• 调整卷积核参数，测试并总结。（必做）
• 使用不同尺寸图片，测试并总结。（必做）

1.实现灰度图的边缘检测、锐化、模糊。

先放个彩图欣赏下：

import matplotlib.pyplot as plt
import torch
from PIL import Image
import numpy as np
def cov2(picture,kernel,strde):
    # picture 为原图像，kernel 为卷积核，strde 为步长
    # x,y为矩阵的行列数
    x1, y1 = picture.shape
    x2, y2 = kernel.shape
    # x_count,y_count是计算在行列上卷积核与原图像的乘积次数,也是卷积后矩阵的行列数
    x3 = int((x1-x2)/strde+1)
    y3 = int((y1-y2)/strde+1)
    # 卷积后生成的新矩阵arr
    arr = np.zeros((x3,y3))
    # 先行后列进行卷积
    for i in range(0,y3):
        for j in range(0,x3):
            s = 0
            for m in range(0,x2):
                for n in range(0,y2):
                    s = s + picture[m+j*strde][n+i*strde]*kernel[m][n]
            arr[j][i] = s
    return arr

im = Image.open('申鹤.jpg').convert('L')  # 以灰度图形式读入图像
im = np.array(im,dtype='float')  # 将原图转化为矩阵形式
plt.figure(1)
plt.subplot(2,2,1)
plt.title('im')
plt.imshow(im,cmap='gray')
# 边缘检测
# 定义卷积核
kernel1 = np.array([[-1,-1,-1],[-1,9,-1],[-1,-1,-1]])
# 开始卷积
t1 = cov2(im,kernel1,1)
plt.subplot(2,2,2)
plt.title('bianyuan')
plt.imshow(t1,cmap='gray')
# plt.show()

# 模糊
# 定义卷积核
kernel2 = np.array([[0.0625,0.125,0.0625],[0.125,0.25,0.125],[0.0625,0.125,0.0625]])
# 开始卷积
t2 = cov2(im,kernel2,1)
plt.subplot(2,2,3)
plt.title('blur')
plt.imshow(t2,cmap='gray')
# plt.show()


# 锐化
kernel3 = np.array([[0,-4,0],[-4,17,-4],[0,-4,0]])
# 开始卷积
t3 = cov2(im,kernel3,1)
plt.subplot(2,2,4)
plt.title('sharpen')
plt.imshow(t3,cmap='gray')
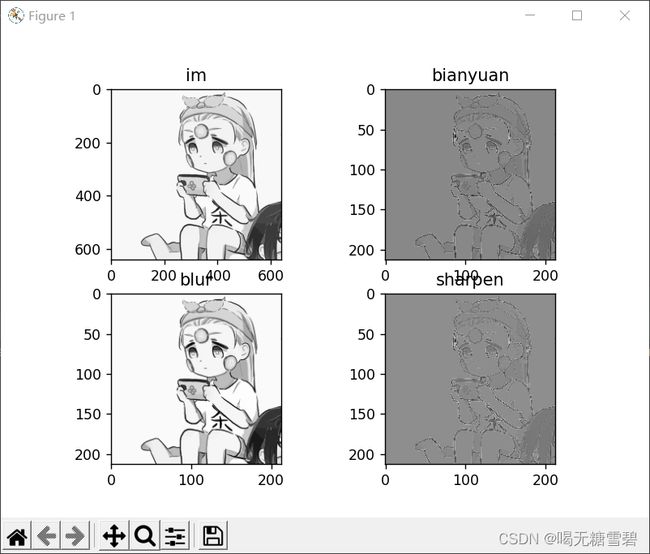
plt.show()

运行结果：

说实话，个人看起来变化有点不太明显，可能因为我用的自己写的粗糙的卷积函数，效率太低了。想把卷积核变大一点的话程序运行时间太久了，所以就放弃了，使用nn库里的卷积函数应该能更好些。

边缘检测：

边缘检测（edge detction）对图像识别中的特征提取是非常有作用的，边缘检测卷积核都有一个共同点，就是能够突出图片矩阵中变化剧烈的位置。矩阵如下所示，三种边缘检测核的效果是越来越明显，主要原因就是加强了卷积核中[2, 2]位置处与周围元素的区别，图片中变化剧烈位置的在加权后，数值大的更大，数值小的更小，形成了边缘检测效果。

锐化：

锐化（sharpen)的本质还是利用的边缘检测的原理，放大[2, 2]位置与周围元素的权重的区别。与边缘检测权重和为 0 相比，锐化卷积核中所有权重加起来后的值为 1。当权重和大于 1 时，会整体使图片变亮，小于 1 会变暗，等于 1 就会保留原始亮度，所以锐化卷积核保留了原始图形的亮度，而上述的三个边缘检测核使图像变暗。
模糊：

盒模糊

在盒模糊卷积核中，所有位置的权重均为 1/9，所以[2, 2]位置处的元素值会以一个相同权重与周围变得更相似，达到均匀模糊的效果

高斯模糊

高斯模糊卷积核依赖的是高斯函数，所以卷积核的值是围绕着中心点分布的，离中心点越近，贡献也就越大，所以权重值就越高

了解更多请移步： 图像处理中的卷积核

2.调整卷积核参数，测试并总结。

（1）更改步长

步长为1时：

步长为3时：

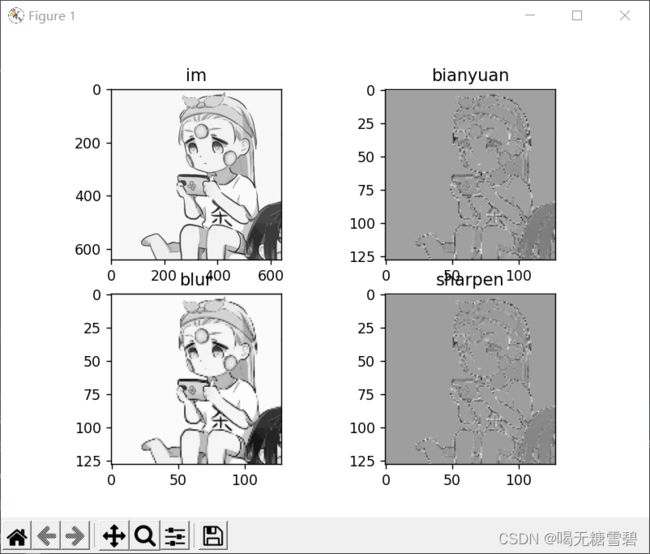
步长为5时：

 可以看到，随着步长的增加，图像变得逐渐模糊

（2）增加padding

开始设计的卷积函数没有padding参数，这里对函数进行了更新，加入了padding这一参数

import matplotlib.pyplot as plt
import torch
from PIL import Image
import numpy as np
def cov2(picture,kernel,strde,padding=0):
    # picture 为原图像，kernel 为卷积核，strde 为步长
    # x,y为矩阵的行列数
    if padding!=0:
        picture = np.pad(picture,padding,constant_values=0)
    x1, y1 = picture.shape
    x2, y2 = kernel.shape
    # x_count,y_count是计算在行列上卷积核与原图像的乘积次数,也是卷积后矩阵的行列数
    x3 = int((x1-x2)/strde+1)
    y3 = int((y1-y2)/strde+1)
    # 卷积后生成的新矩阵arr
    arr = np.zeros((x3,y3))
    # 先行后列进行卷积
    for i in range(0,y3):
        for j in range(0,x3):
            s = 0
            for m in range(0,x2):
                for n in range(0,y2):
                    s = s + picture[m+j*strde][n+i*strde]*kernel[m][n]
            arr[j][i] = s
    return arr

im = Image.open('申鹤.jpg').convert('L')  # 以灰度图形式读入图像
im = np.array(im,dtype='float')  # 将原图转化为矩阵形式
plt.figure(1)
plt.subplot(2,2,1)
plt.title('im')
plt.imshow(im,cmap='gray')
# 边缘检测
# 定义卷积核
kernel1 = np.array([[-1,-1,-1],[-1,9,-1],[-1,-1,-1]])
# 开始卷积
t1 = cov2(im,kernel1,1,5)
plt.subplot(2,2,2)
plt.title('bianyuan')
plt.imshow(t1,cmap='gray')
# plt.show()


# 模糊
# 定义卷积核
kernel2 = np.array([[0.0625,0.125,0.0625],[0.125,0.25,0.125],[0.0625,0.125,0.0625]])
# 开始卷积
t2 = cov2(im,kernel2,1,5)
plt.subplot(2,2,3)
plt.title('blur')
plt.imshow(t2,cmap='gray')
# plt.show()


# 锐化
kernel3 = np.array([[0,-4,0],[-4,17,-4],[0,-4,0]])
# 开始卷积
t3 = cov2(im,kernel3,1,5)
plt.subplot(2,2,4)
plt.title('sharpen')
plt.imshow(t3,cmap='gray')
plt.show()

运行结果：

padding为0：

padding为2：

padding为5：

 在做这题时可能因为我选的图片边缘地方基本都没啥特征吧，加入padding时比较图像变化还是比较困难的，然后我就多试了几组padding，原本以为能很清晰呢，结果发现照片多出来一个黑框，这才想道卷积核就3*3那么大，padding最好的效果可能也就到2或3吧，因此padding也不是越大越好，这得根据卷积核的大小来制定（个人理解）。

另外就是在设计padding这个参数时发现了np.pad()这个函数，用来给numpy数组的边缘进行数值填充的，就等于增加padding的作用。真不错，又找到一个不知道以后啥时候用但觉得很方便的函数。

详情请移步：np.pad()的用法

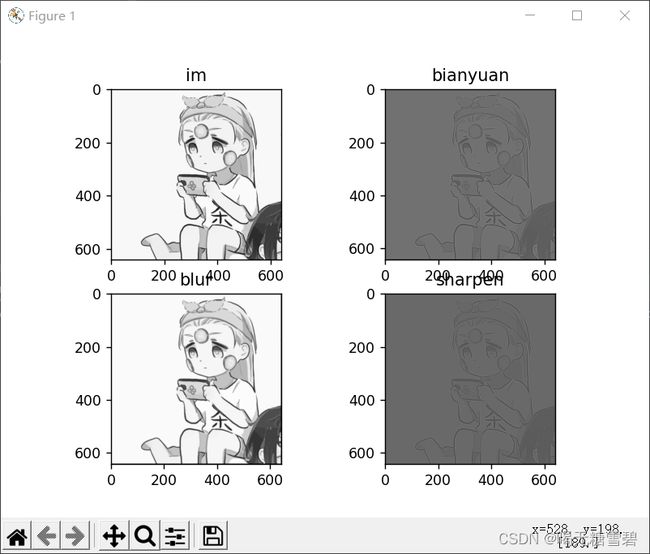
3.使用不同尺寸图片，测试并总结。

正好用上面的表情包来做一下

实验结果：

总结：

在这次实验里我自己动手对卷积函数进行了编写，虽然效率低下导致没法用比较大的卷积核吧，但终究也磕磕绊绊完成了这次试验，不过还是有很大收获的，毕竟自己写的过程中对卷积的理解也更深了，而且在各种参数怎么设置，功能怎么实现方面加深我对知识的印象，同时也提高了写代码的能力。最后想小小吐槽一下，各位大佬程序员写代码的时候真的都不屑于写注释吗，，我这种小弱鸡去看代码学习的时候真的很容易懵呀，怎么也得把参数是什么，函数功能啥的浅浅的标记一下吧，虽然我比较菜吧，但我能写注释还是会写的（就是语言似乎不太高级），希望以后能因为我代码写得好又很会注释被后来学习的人夸吧，当然，现在还是老老实实当个菜鸟吧。

参考：

有很多参考，不过文中已经都列出来了，就不全部重新列出来了，毕竟我估计是最后交作业的了，时间上有着些许紧张。

知乎：如何通俗易懂的解释卷积

 深度学习之卷积