python-Logistic回归分类模型
Logistic回归分类模型的应用
①自定义绘制ks曲线的函数
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
font = {
'family': 'FangSong',
'weight': 'bold',
'size': 12
}
matplotlib.rc("font", **font)
# 自定义绘制ks曲线的函数
def plot_ks(y_test, y_score, positive_flag):
# 对y_test,y_score重新设置索引
y_test.index = np.arange(len(y_test))
# 构建目标数据集
target_data = pd.DataFrame({'y_test': y_test, 'y_score': y_score})
# 按y_score降序排序
target_data.sort_values(by='y_score', ascending=False, inplace=True)
# 自定义分位点
cuts = np.arange(0.1, 1, 0.1)
# 计算各分位点对应的Score值
index = len(target_data.y_score)*cuts
scores = target_data.y_score.iloc[index.astype('int')]
# 根据不同的Score值,计算Sensitivity和Specificity
Sensitivity = []
Specificity = []
for score in scores:
# 正例覆盖样本数量与实际正例样本量
positive_recall = target_data.loc[(target_data.y_test == positive_flag) & (target_data.y_score > score), :].shape[0]
positive = sum(target_data.y_test == positive_flag)
# 负例覆盖样本数量与实际负例样本量
negative_recall = target_data.loc[(target_data.y_test != positive_flag) & (target_data.y_score <= score), :].shape[0]
negative = sum(target_data.y_test != positive_flag)
Sensitivity.append(positive_recall/positive)
Specificity.append(negative_recall/negative)
# 构建绘图数据
plot_data = pd.DataFrame({
'cuts': cuts,
'y1': 1-np.array(Specificity),
'y2': np.array(Sensitivity),
'ks': np.array(Sensitivity) - (1-np.array(Specificity))
})
# 寻找Sensitivity和1-Specificity之差的最大值索引
max_ks_index = np.argmax(plot_data.ks)
plt.plot([0]+cuts.tolist()+[1], [0]+plot_data.y1.tolist()+[1], label='1-Specificity')
plt.plot([0] + cuts.tolist() + [1], [0] + plot_data.y2.tolist() + [1], label='Sensitivity')
# 添加参考线
plt.vlines(plot_data.cuts[max_ks_index], ymin=plot_data.y1[max_ks_index], ymax=plot_data.y2[max_ks_index], linestyles='--')
# 添加文本信息
plt.text(x=plot_data.cuts[max_ks_index] + 0.01,
y=plot_data.y1[max_ks_index] + plot_data.ks[max_ks_index]/2,
s='KS=%.2f'%plot_data.ks[max_ks_index])
# 显示图例
plt.legend()
# 显示图形
plt.show()②模型的构建
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import matplotlib
from ks曲线 import plot_ks
from sklearn import linear_model
from sklearn import model_selection
font = {
'family': 'FangSong',
'weight': 'bold',
'size': 12
}
matplotlib.rc("font", **font)
# 读取数据 Run or Walk.csv
sports = pd.read_csv('./data/Run or Walk.csv', delimiter=',')
# 提取出所有自变量名称
predictors = sports.columns[4:]
# 构建自变量矩阵
x = sports.loc[:, predictors]
# 提取y变量值
y = sports.activity
# 将数据拆分成训练集和测试集
x_train, x_test, y_train, y_test = model_selection.train_test_split(x, y, test_size=0.25, random_state=1234)
# 利用训练集建模
sklearn_logistic = linear_model.LogisticRegression()
sklearn_logistic.fit(x_train, y_train)
# 返回模型各个参数
intercept = sklearn_logistic.intercept_ # [4.35613952]
coef = sklearn_logistic.coef_ # [[ 0.48533325 6.86221041 -2.44611637 -0.01344578 -0.1607943 0.13360777]]
print(intercept, coef)③模型的预测
sklearn_predict = sklearn_logistic.predict(x_test)
# 预测结果统计
res = pd.Series(sklearn_predict).value_counts()
# 0 12121
# 1 10026
# dtype: int64
print(res)④模型评估
常用 混淆矩阵、ROC曲线和K-S曲线
# 导入第三方模块
from sklearn import metrics
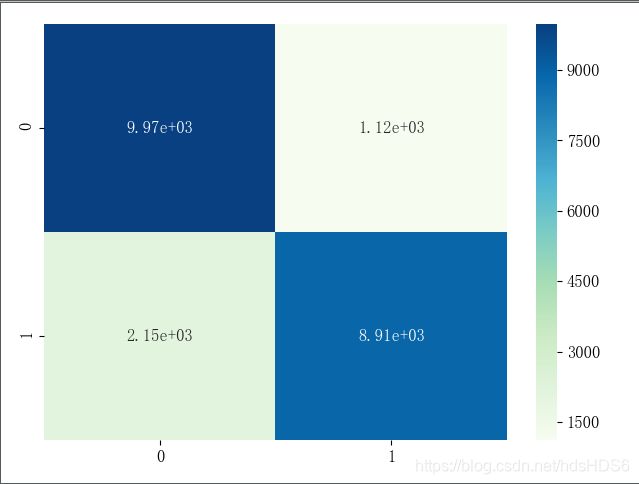
# 混淆矩阵
cm = metrics.confusion_matrix(y_test, sklearn_predict, labels=[0, 1])
# [[9971 1120]
# [2150 8906]]
print(cm)
# 准确率 Accuracy
Accuracy = metrics.scorer.accuracy_score(y_test, sklearn_predict)
# 正例覆盖率
Sensitivity = metrics.scorer.recall_score(y_test, sklearn_predict)
# 负例覆盖率
Specificity = metrics.scorer.recall_score(y_test, sklearn_predict, pos_label=0)
print("准确率%.2f%%" % (Accuracy*100))
print("正例覆盖率%.2f%%" % (Sensitivity*100))
print("负例覆盖率%.2f%%" % (Specificity*100))
# 准确率85.24%
# 正例覆盖率80.55%
# 负例覆盖率89.90%
# 对混淆矩阵做可视化
'''
颜色越深的区块代表样本量越多
'''
# 热力图
sns.heatmap(cm, annot=True, fmt='.2e', cmap='GnBu')
# 显示图形
plt.show()
# 调用自定义函数,绘制K-S曲线
# 计算对应的概率值
y_score = sklearn_logistic.predict_proba(x_test)[:, 1]
plot_ks(y_test, y_score, 1)
print(y_score)import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import matplotlib
from ks曲线 import plot_ks
from sklearn import model_selection
import statsmodels.api as sm
from sklearn import metrics
font = {
'family': 'FangSong',
'weight': 'bold',
'size': 12
}
matplotlib.rc("font", **font)
# ----------------------------------------第一步建模----------------------------------------- #
# 读取数据 Run or Walk.csv
sports = pd.read_csv('./data/Run or Walk.csv', delimiter=',')
# 提取出所有自变量名称
predictors = sports.columns[4:]
# 构建自变量矩阵
x = sports.loc[:, predictors]
# 提取y变量值
y = sports.activity
# 将数据拆分成训练集和测试集
x_train, x_test, y_train, y_test = model_selection.train_test_split(x, y, test_size=0.25, random_state=1234)
# 为训练集和测试集的x矩阵添加常数列1
x_train2 = sm.add_constant(x_train)
x_test2 = sm.add_constant(x_test)
# 拟合logistic模型
sm_logistic = sm.formula.Logit(y_train, x_train2).fit()
# 返回模型参数
params = sm_logistic.params
'''
Current function value: 0.324875
Iterations 8
const 4.388537
acceleration_x 0.489617
acceleration_y 6.906590
acceleration_z -2.459638
gyro_x -0.014715
gyro_y -0.161164
gyro_z 0.134655
dtype: float64
'''
print(params)
# --------------------------------------第二步 预测构建混淆矩阵-------------------------------------- #
# m模型在测试集上预测
sm_y_probability = sm_logistic.predict(x_test2)
# 根据概率值,将观测进行分类,以0.5为阈值
sm_pred_y = np.where(sm_y_probability >= 0.5, 1, 0)
# 混淆矩阵
cm = metrics.confusion_matrix(y_test, sm_pred_y, labels=[0, 1])
print(cm)
# 混淆矩阵的热力图
sns.heatmap(cm, annot=True, fmt='.2e', cmap='GnBu')
# 显示图形
plt.show()
# --------------------------------------第三步 绘制ROC曲线-------------------------------------- #
# 计算真正率和假正率
fpr, tpr, threshold = metrics.roc_curve(y_test, sm_y_probability)
# 计算auc的值
roc_auc = metrics.auc(fpr, tpr)
# 绘制面积图
plt.stackplot(fpr, tpr, color='steelblue', alpha=0.5, edgecolor='black')
# 添加边际线
plt.plot(fpr, tpr, color='black', lw=1)
# 添加对角线
plt.plot([0, 1], [0, 1], color='red', linestyle='--')
# 添加文本信息
plt.text(0.5, 0.3, 'ROC curve (area = %.2f)' % roc_auc)
# 添加x轴与y轴标签
plt.xlabel("1-Specificity")
plt.ylabel("Sencitivity")
# 显示图形
plt.show()
# --------------------------------------第四步 绘制K-S曲线-------------------------------------- #
# 调用自定义函数,绘制K-S曲线
sm_y_probability.index = np.arange(len(sm_y_probability))
plot_ks(y_test=y_test, y_score=sm_y_probability, positive_flag=1)