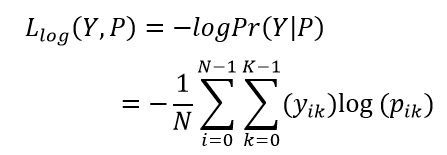机器学习学习笔记之：loss function损失函数及activation function激活函数

之所以把损失函数和激活函数放在一起做个总结，是因为本身这两都带函数，都是机器学习中的内容，很容易混在一起，第二点，这两者总是一起出现，根据任务的不同，可能出现不同的排列组合。因此想一起整理一下。

 

不同的机器学习方法的损失函数

Different Loss functions for different machine learning Methods

不同的机器学习方法，损失函数不一样，

quadratic loss (平方误差损失函数，线性回归)

logLoss (对数损失函数，LR，逻辑回归)

hinge loss (合页损失函数，SVM，支持向量机)

exp-loss (指数损失函数，AdaBoost)

cross-entropy loss (交叉熵损失函数，CNN，DNN等等, 其中

---------------------------------------------------------------------------------------

二分类（binary classification）

binary_crossentropy +sigmoid，

sigmoid+BCE, for the binary classification.

binary_crossentropy（亦称作对数损失，logloss）通常简称为BCE，BCE适用于二分类。bce 是对数损失函数的实例化

---------------------------------------------------------------------------------------

多分类（multi-class classification,一个样本只属于多个分类中的一个，比如手写数字，一个数字图片样本只属于一个类，），

categorical_crossentropy+softmax，

softmax+CE, for the multi-class classification

categorical_crossentropy：亦称作多类的对数损失，注意使用该目标函数时，需要将标签转化为形如(nb_samples, nb_classes)的二值序列。通常简称为CE，CE用于多分类,

sparse_categorical_crossentrop：如上，但接受稀疏标签。注意，使用该函数时仍然需要你的标签与输出值的维度相同，你可能需要在标签数据上增加一个维度：np.expand_dims(y,-1)

 

---------------------------------------------------------------------------------------

多标签分类（multi-label classification), 一个样本可能有多个标签，比如一张图片有猫有狗有兔子 带多个标签的 )，binary_crossentropy+sigmoid

---------------------------------------------------------------------------------------

• 交叉熵损失函数的原理：

• 交叉熵是信息论领域的一种度量方法，它建立在熵的基础上，通常计算两种概率分布之间的差异。

• 交叉熵损失函数经常用于分类问题中，特别是神经网络分类问题。交叉熵是用来描述两个分布的距离的，神经网络训练的目的就是使 g(x) 逼近 p(x)。相比平方差函数，交叉熵函数的很好的特质是没有导数一项，这样一来不会受到饱和性的影响了。当误差大的时候，权重更新就快，当误差小的时候，权重的更新就慢。

• The crossentropy is used to describe the distance between two distribution，the binary crossentropy AKA logloss, ot BCE, is more suitable for binary classification.Furthermore, comparing with MSE, 

• kullback_leibler_divergence:从预测值概率分布Q到真值概率分布P的信息增益,用以度量两个分布的差异.KL-散度

 

一些损失函数的比较：

相比较均方误差损失函数+sigmoid 

使用交叉熵+sigmoid可以解决平方损失函数权重更新过慢的问题，具有“误差大的时候，权重更新快；误差小的时候，权重更新慢”的良好性质。

 

 

激活函数

在多层神经网络中，上层节点的输出和下层节点的输入之间具有一个函数关系，这个函数称为激活函数（又称激励函数）

激活函数的作用：

将原来的线性变换，转换为非线性的变化，从而提升模型的泛化程度。

从线性模型==》非线性模型。

用于隐藏层的激活函数，使用relu以及relu的变种作为激活函数

对于二分类网络，使用 sigmoid 作为其输出层的激活函数；

对于多分类网络，使用 softmax 作为其输出层的激活函数

 

 

在构建完神经网络的架构（包括网络结构，layer的结构以及组成成分，损失函数以后，就要对模型进行求解）

求解的方法主要有随机梯度下降法（Stochastic Gradient Descent），其中包含一些参数，比如说学习率，momentum（动量的作用是 averages the current gradient with those from previous mini-batches,smoothen the gradient），nesterov（use Nestorov momentum）等等。还有一些其他的optimizer优化器，比如说adam

在之前的神经网络的构建中，中间层多使用sigmoid的激活函数来模拟神经元，从而使得模型从线性变为非线性，让模型更加的泛化。但是sigmoid的激活函数会使得训练过程中产生梯度消失和梯度爆炸的问题，主要是因为涉及到二阶导，如果层数过深，反向传播会越来越小，所以这个激活函数会有一些问题。因此在使用的过程中，深度学习中间层的激活函数往往会选择relu函数以及relu函数的变体。

在最后的一层使用sigmoid激活函数，通常使用交叉熵的损失函数，而不是使用MSE，均方差损失函数，来解决平方损失函数权重更新慢的问题。

对于多层神经网络，用于隐藏层的激活函数每个隐藏层都使用Sigmoid函数作为激励函数时，很容易引起梯度消失的问题。

 

sigmoid 存在的问题？

1）sigmoid函数饱和使梯度消失(Sigmoid saturate and kill gradients)

2）sigmoid函数输出不是“零为中心”(zero-centered)（图上来看就是不过零点）。如果输入x正数，反向传播到某一层就是全正或全负（使用tanh(x)可以解决输出非零中心）

3)使用指数计算消耗计算资源

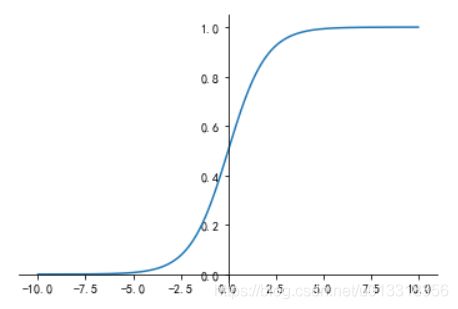
Sigmoid函数图像（这里可以看到激活函数并没有以0为中心（没有经过零点），这样的影响主要是，模型为了收敛，速度会比较慢，（输入和参数变化方向一致））

什么是梯度消失问题？

那么当神经网络特别深的时候，如果使用饱和的激活函数，比如（Sigmoid函数）, 梯度呈指数级衰减，导数在每一层至少会被压缩为原来的1/4，当z值绝对值特别大时，导数趋于0。从输出层不断向输入层反向传播训练时，导数很容易逐渐变为0，使得权重和偏差参数无法被更新，导致神经网络无法被优化，训练永远不会收敛到良好的解决方案。 这被称为梯度消失问题。

什么是梯度爆炸？

当我们将w初始化为一个较大的值时，同梯度消失类似，当神经网络很深时，梯度呈指数级增长，最后到输入时，梯度将会非常大，我们会得到一个非常大的权重更新，这就是梯度爆炸的问题，在循环神经网络中最为常见.

怎么解决梯度消失/梯度爆炸问题：

1）为了解决梯度消失的问题，通常使用ReLu及其变体，这也是最常用的激活函数。

注意这里的激活函数是中间层的激活函数。

对于二分类，最后一层还是sigmoid，对于多分类，最后一层还是softmax函数。

2）使用batchnormal 批量规范化（Batch Normalization）

3）梯度截断（Gradient Clipping）

4）更好的参数初始化方式

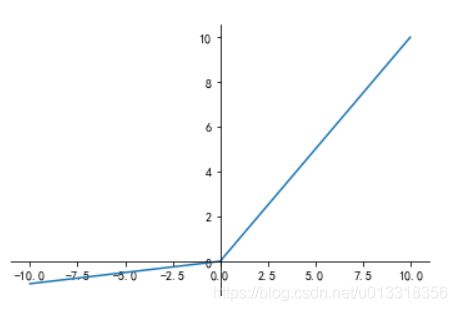
Relu函数的图像

Relu主要的优点是

1.缓解梯度消失的问题，

2.加快收敛的速度

3.ReLu涉及的计算，相比sigmoid和 tanh更加简单

主要缺点是：

1.涉及到神经元死亡（Dead ReLU），无法更新。

tips：

 Dead ReLU Problem(神经元坏死现象)：ReLU在负数区域被kill的现象叫做dead relu。ReLU在训练的时很“脆弱”。在x<0时，梯度为0。这个神经元及之后的神经元梯度永远为0，不再对任何数据有所响应，导致相应参数永远不会被更新。

产生这种现象的两个原因：参数初始化问题；learning rate太高导致在训练过程中参数更新太大。

解决方法：采用Xavier初始化方法，以及避免将learning rate设置太大或使用adagrad等自动调节learning rate的算法。

2.输出的不是zero-centered

 

为了解决Dead ReLU的问题

可以使用Leaky Relu来解决dead Relu的问题

另外一种激活函数是：

Softmax函数，主要用于多分类问题

Softmax函数的作用就是将每个类别所对应的输出分量归一化，使各个分量的和为1。可以理解为，能将任意是输入值转化为概率。

Softmax主要用于多分类任务的激活函数，一般用在神经网络的输出端。

 

逻辑回归以及感知机使用的激活函数、损失函数：

逻辑回归二分类 损失函数：对数损失函数（极大似然）  激活函数：sigmoid

感知机二分类( 1 linear function)    损失函数：均方损失函数（即错误点到分离平面的距离，最小化这个值）  激活函数：sign函数 or  threshold

逻辑回归多分类( 1 linear function for each class)   损失函数：交叉熵损失函数 激活函数：softmax函数

多层感知机MLP做分类 损失函数：交叉熵损失函数 激活函数：softmax

所以逻辑回归多分类可以看成一种特殊的多层感知机。

 

总结：

损失函数通常由问题来定义，通过极小化损失函数，来更新模型参数，获取模型的最佳参数。

不同的损失函数，收敛的速度不一样。因此模型的收敛速度也不一样。

激活函数通常用来使得模型由线性变为非线性，在深度学习中，通常中间层用relu及其变体（防止梯度消失或者梯度爆炸），最后一层根据任务是单分类还是多分类，选择合适的激活函数比如sigmoid或者softmax.

具体选择某种激活函数的原因，也是基于收敛的速度，以及计算的消耗等等。

 

参考：

https://blog.csdn.net/perfect1t/article/details/88199179 机器学习之常见的损失函数(loss function) 

https://blog.csdn.net/junjun150013652/article/details/81274958 梯度消失和梯度爆炸

https://blog.csdn.net/lyy14011305/article/details/88664518 二分类，多分类，多标签分类的选择

https://zhuanlan.zhihu.com/p/92412922 常见激活函数优缺点与dead relu problem