RNN，LSTM，GRU解析

1. RNN

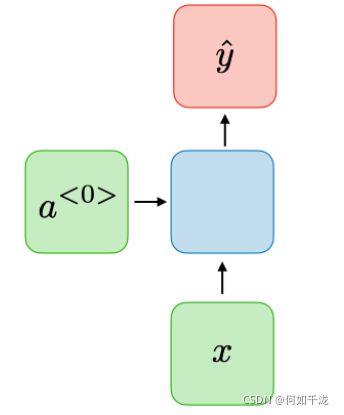
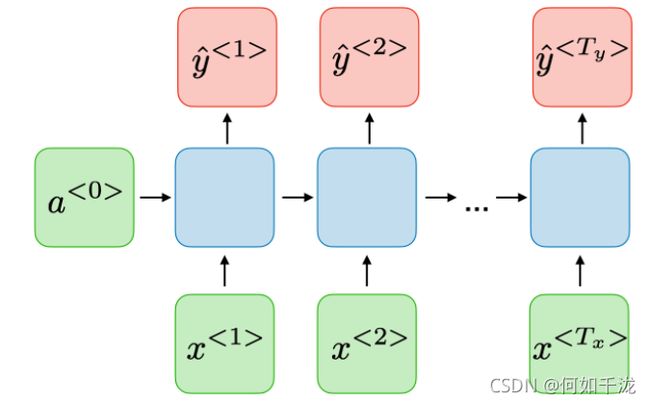
1.1 RNN的结构

对于每一个时间步$t$而言

• $a^{<t>}=g(W_{aa}{a}^{<t-1>}+W_{ax}{x}^{<t>}+b_a)$
• $y^{<t>}=W_{ya}{a}^{<t>}+b_y$

其中$W_{aa},W_{ax},W_{ya},b_a,b_y$是每个循环单元共享的参数，$g$是激活函数$Tanh$

1.2 RNN的种类

1. 一对一
   

2. 一对多
   

3. 多对一
   

4. 多对多(输入序列和输出序列长度相等)
   

5. 多对多(输入序列和输出序列长度不相等)
   

1.3 RNN的优缺点

1. 优点
   • 可以处理任何长度的输出
   • 模型大小不随输入大小增加而增大
   • 计算考虑了历史信息
   • 权重是跨时间步共享的
2. 缺点
   • 计算缓慢
   • 很难访问很久之前的信息
   • 不能考虑当前时间步后的未来信息

1.4 RNN参数详解torch.nn.RNN

1. 参数
   • input_size：输入序列x的特征长度
   • hidden_size：隐藏层的特征长度
   • num_layers：rnn层的数目。如果将其设置为2，将意味着将两个 RNN 堆叠在一起形成一个堆叠的 RNN，第二个 RNN 接收第一个 RNN 的输出并计算最终结果。默认值为1
   • nonlinearity：非线性层，默认为tanh
   • bias：是否使用bias，默认为True
   • batch_first：如果为True，则输入和输出的tensor形状必须提供成(batch, seq, feature)而不是(seq,batch,feature)，默认为False
   • dropout：在除最后一层之外的每个 RNN 层的输出上引入一个 Dropout 层，dropout概率等于dropout。默认为0
   • bidirectional：如果为True，则为双向RNN，默认为False
2. 输入
   • input：当batch_first为False时，形状为(seq_len, batch_size, input_size)，否则为(batch_size, seq_len,input_size)
   • h_0：形状为(D*num_layer, batch_size, hidden_size)。其中D=2 if bidirectional==True else 1
3. 输出
   • output：当batch_first为False时，形状为(seq_len, batch_size,D*hidden_size)，否则为(batch_size, seq_len,D*hidden_size)。其中D=2 if bidirectional==True else 1
   • h_n：形状为(D*num_layer, batch_size, hidden_size)。其中D=2 if bidirectional==True else 1
4. 例子解析

   import torch
   import torch.nn as nn
   
   rnn = nn.RNN(10, 20, 2)
   input = torch.randn(5, 3, 10)
   h_0 = torch.randn(2, 3, 20)
   output, h_n = rnn(input, h_0)
   
   output.shape
   Out[1]: torch.Size([5, 3, 20])
   
   h_n.shape
   Out[2]: torch.Size([2, 3, 20])
   

2. LSTM

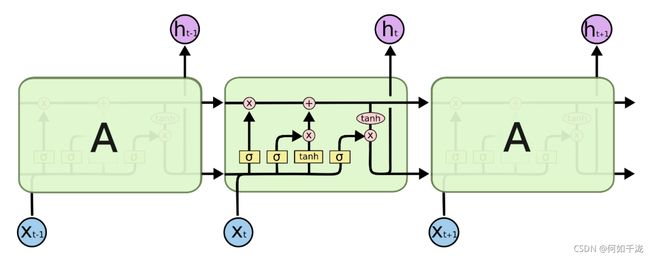
2.1 LSTM的结构

其中

• $\sigma$：sigmoid gate layer(其输出是一个0-1的数，用来控制信息输出。0代表不让任何信息通过、1代表让任何信息通过)
• $x_t$：输入
• $h_t$：输出

2.1.1 forget gate layer

• $f_t\in [0,1]$：用来控制忘记多少历史信息

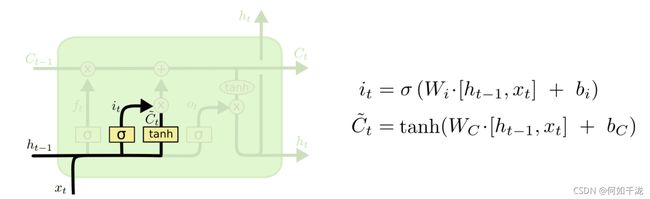
2.1.2 input gate layer

• $C_t$：当前状态临时信息
• $i_t\in [0,1]$：用来控制保留多少历史信息

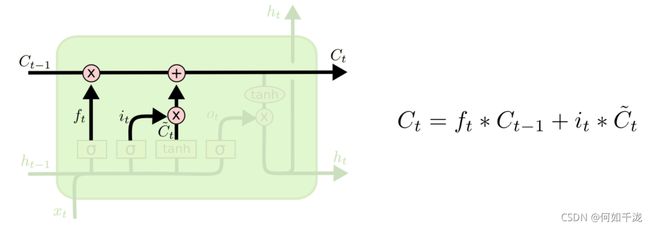
2.1.3 当前状态实际信息

• $f_t$：控制让多少历史信息通过
• $C_{t-1}$：历史信息
• $i_t$：控制让多少当前信息通过
• $C_t$：当前信息

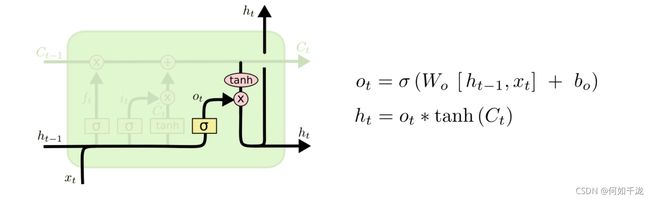
2.1.4 output gate layer

• $o_t$：控制最后输出多少信息
• $h_t$：输出

2.2 LSTM的种类

同RNN一样，只不过将RNN cell换成LSTM cell

2.3 LSTM的优缺点

1. 优点
   • 其结构类似于ResNet, 消除了一些梯度消失/爆炸的问题
2. 缺点：
   • 计算费时，每个cell有4个全连接层

2.4 LSTM参数解析torch.nn.LSTM

1. 参数
   • input_size：输入序列x的特征长度
   • hidden_size：隐藏层的特征长度
   • num_layers：rnn层的数目。如果将其设置为2，将意味着将两个 RNN 堆叠在一起形成一个堆叠的 RNN，第二个 RNN 接收第一个 RNN 的输出并计算最终结果。默认值为1
   • bias：是否使用bias，默认为True
   • batch_first：如果为True，则输入和输出的tensor形状必须提供成(batch, seq, feature)而不是(seq,batch,feature)，默认为False
   • dropout：在除最后一层之外的每个 RNN 层的输出上引入一个 Dropout 层，dropout概率等于dropout。默认为0
   • bidirectional：如果为True，则为双向RNN，默认为False
   • proj_size：如果大于0，将使用具有相应大小投影的 LSTM（简单来说就是在原有基础上的输出层后增加个全连接层，使其投影到指定大小。即$h_t=W_{hr}{h}_t$）。默认为0
2. 输入
   • input：当batch_first为False时，形状为(seq_len, batch_size, input_size)，否则为(batch_size, seq_len,input_size)
   • h_0：形状为(D*num_layer, batch_size, output_size)。其中D=2 if bidirectional==True else 1, output_size=proj_size if proj_size>0 else hidden_size
   • c_0：形状为(D*num_layer, batch_size, hidden_size)。其中D=2 if bidirectional==True else 1
3. 输出
   • output：当batch_first为False时，形状为(seq_len, batch_size,D*hidden_size)，否则为(batch_size, seq_len,D*hidden_size)。其中D=2 if bidirectional==True else 1
   • h_n：形状为(D*num_layer, batch_size, output_size)。其中D=2 if bidirectional==True else 1, output_size=proj_size if proj_size>0 else hidden_size
   • c_n：形状为(D*num_layer, batch_size, hidden_size)。其中D=2 if bidirectional==True else 1
4. 例子解析

   import torch
   import torch.nn as nn
   
   lstm = nn.LSTM(10, 20, 2, proj_size=15)
   input = torch.randn(5, 3, 10)
   h_0 = torch.randn(2, 3, 15)
   c_0 = torch.randn(2, 3, 20)
   output, (h_n, c_n) = lstm(input, (h_0, c_0))
   
   output.shape
   Out[1]: torch.Size([5, 3, 15])
   
   h_n.shape
   Out[2]: torch.Size([2, 3, 15])
   
   c_n.shape
   Out[3]: torch.Size([2, 3, 20])
   

3. GRU

3.1 GRU的结构

• $r_t$：重置门，用来重置历史信息$h_{t-1}$
• $z_t$：更新门，用来更新当前时刻的状态
• $h_t$：当前时刻的临时状态，其输入是当前时刻的输入$x_t$和经过重置后的历史信息$r_t\cdot h_{t-1}$
• $h_t$：当前时刻的状态

3.2 GRU的种类

同RNN一样，只不过将RNN cell更换为GRU cell

3.3 GRU与LSTM比较

• 将忘记门和输入门组合成一个更新门
• 合并了单元状态和隐藏状态

3.4 GRU详解torch.nn.GRU

1. 参数
   • input_size：输入序列x的特征长度
   • hidden_size：隐藏层的特征长度
   • num_layers：rnn层的数目。如果将其设置为2，将意味着将两个 RNN 堆叠在一起形成一个堆叠的 RNN，第二个 RNN 接收第一个 RNN 的输出并计算最终结果。默认值为1
   • bias：是否使用bias，默认为True
   • batch_first：如果为True，则输入和输出的tensor形状必须提供成(batch, seq, feature)而不是(seq,batch,feature)，默认为False
   • dropout：在除最后一层之外的每个 RNN 层的输出上引入一个 Dropout 层，dropout概率等于dropout。默认为0
   • bidirectional：如果为True，则为双向RNN，默认为False
2. 输入
   • input：当batch_first为False时，形状为(seq_len, batch_size, input_size)，否则为(batch_size, seq_len,input_size)
   • h_0：形状为(D*num_layer, batch_size, hidden_size)。其中D=2 if bidirectional==True else 1
3. 输出
   • output：当batch_first为False时，形状为(seq_len, batch_size,D*hidden_size)，否则为(batch_size, seq_len,D*hidden_size)。其中D=2 if bidirectional==True else 1
   • h_n：形状为(D*num_layer, batch_size, hidden_size)。其中D=2 if bidirectional==True else 1
4. 例子解析

   import torch
   import torch.nn as nn
   
   rnn = nn.GRU(10, 20, 2)
   input = torch.randn(5, 3, 10)
   h_0 = torch.randn(2, 3, 20)
   output, h_n = rnn(input, h_0)
   
   output.shape
   Out[1]: torch.Size([5, 3, 20])
   
   h_n.shape
   Out[2]: torch.Size([2, 3, 20])
   

4. RNN为啥不能学习很久的历史信息？

我们将RNN简单表示为

1. 隐状态：
   $$h_t=tanh(W_I{x}_t+W_R{h}_{t-1})$$
2. 输出：
   $$y_t=W_O{h}_t$$

假设$E=\frac{1}{2}({\hat{y}}_t-y_t{)}^2$, 对于时间步长$t$，我们通过链式法则计算梯度
$$\frac{\partial E_t}{\partial W_R}=\sum _{i=0}^t\frac{\partial E_t}{\partial y_t}\frac{\partial y_t}{\partial h_t}\frac{\partial h_t}{\partial h_i}\frac{\partial h_i}{\partial W_R}$$

其中
$$\frac{\partial E_t}{\partial y_t}={\hat{y}}_t-y_t$$
$$\frac{\partial y_t}{\partial h_t}=W_O$$
$$\frac{\partial h_t}{\partial h_i}=\frac{\partial h_t}{\partial h_{t-1}}\frac{\partial h_{t-1}}{\partial h_{t-2}}...\frac{\partial h_{i+1}}{\partial h_i}=\prod _{k=i}^{t-1}\frac{\partial h_{k+1}}{\partial h_k}$$
$$\frac{\partial h_i}{\partial W_R}=h_{i-1}$$

现在我们来计算
$$\frac{\partial h_{k+1}}{\partial h_k}=tan{h}^{\prime }\cdot W_R$$

因此，如果我们反向传播$k$个时间步长，则梯度会变成
$$\frac{\partial h_k}{\partial h_1}=\prod _{i=1}^{k}tan{h}^{\prime }\cdot W_R$$

其中，$tan{h}^{\prime }$总小于1，如果$W_R$大于1，则会发生梯度爆炸；如果$W_R$小于1，则会发生梯度消失。所以RNN无法学习到很久的信息。

5. RNN为啥使用Tanh而不使用relu作为激活函数？

$$\frac{\partial h_k}{\partial h_{k-1}}=(1-h_k^2)W_R$$

1. 当激活函数为$Tanh$时
   由于$Tan{h}^{\prime }(x)=1-Tan{h}^2(x)$，所以当$W_R$很大时，则$h_k$接近于$1$，所以$(1-h_k^2)W_R$很小，故$\frac{\partial h_k}{\partial h_{k-1}}$有界
2. 当激活函数为$ReLU$时
   由于$ReL{U}^{\prime }(x)=\{0,1\}$，所以当$ReL{U}^{\prime }(x)=1$，且$W_R$很大，则$\frac{\partial h_k}{\partial h_{k-1}}$无界

6. LSTM是如何解决梯度爆炸/消失的？

我们将LSTM简单表示为
$$f_t=\sigma (W_f[h_{t-1},x_t])$$
$$i_t=\sigma (W_i[h_{t-1},x_t])$$
$$o_t=\sigma (W_o[h_{t-1},x_t])$$
$$C_t=tanh(W_C[h_{t-1},x_t])$$
$$C_t=f\cdot C_{t-1}+i\cdot C_t$$
$$h_t=o_t\cdot tanh(C_t)$$

RNN之所以会导致梯度爆炸/消失，是因为隐状态求梯度时$\frac{\partial h_{k+1}}{\partial h_k}=tan{h}^{\prime }\cdot W_R$这一项会被累乘多次，所以我们来看看LSTM的隐状态的梯度变化，通过链式求导法则可知：
$$\frac{\partial C_t}{\partial C_{t-1}}=\frac{\partial C_t}{\partial f_t}\frac{\partial f_t}{\partial h_{t-1}}\frac{\partial h_{t-1}}{\partial C_{t-1}}+\frac{\partial C_t}{\partial C_{t-1}}+\frac{\partial C_t}{\partial i_t}\frac{\partial i_t}{\partial h_{t-1}}\frac{\partial h_{t-1}}{\partial C_{t-1}}+\frac{\partial C_t}{\partial C_t}\frac{\partial C_t}{\partial h_{t-1}}\frac{\partial h_{t-1}}{\partial C_{t-1}}$$

现在让我们明确这些导数

$$\frac{\partial C_t}{\partial C_{t-1}}=C_{t-1}{\sigma }^{\prime }(\ast )W_f\cdot o_{t-1}tan{h}^{\prime }(C_{t-1})+f_t+C_t\sigma (\ast )W_i\cdot o_{t-1}tan{h}^{\prime }(C_{t-1})+i_{t}tan{h}^{\prime }(\ast )W_C\cdot o_{t-1}tan{h}^{\prime }(C_{t-1})$$

由于RNN中，$\frac{\partial h_t}{\partial h_{t-1}}$的值要么取大于1要么处于[0, 1]之间，所以经过连乘后会导致梯度爆炸/消失；而在LSTM中，$\frac{\partial C_t}{\partial C_{t-1}}$在任何步长既可以取大于1，也可以取[0, 1]之间(因为$f_t,o_t,i_t,C_{t-1},C_t$可以来调节。例如可以使$f_t$接近1来解决梯度消失，至于梯度爆炸可以设置梯度阈值)

用ResNet的思维来理解，上面介绍LSTM时，提到了其用到了ResNet的思想，通过让$f_t$趋向1，$i_t$趋向0，让历史信息直接流向未来而忽略当前时刻的信息，这样就类似与一个残差结构。

---

项目实战：利用LSTM进行股票预测分析

---

参考链接：

• https://stanford.edu/~shervine/teaching/cs-230/cheatsheet-recurrent-neural-networks
• https://colah.github.io/posts/2015-08-Understanding-LSTMs/
• https://weberna.github.io/blog/2017/11/15/LSTM-Vanishing-Gradients.html
• https://www.zhihu.com/question/34878706