《Deep residual shrinkage networks for fault diagnosis》 基于深度残差收缩网络的故障诊断(翻译与python代码)
基于深度残差收缩网络的故障诊断(翻译)
论文连接:https://ieeexplore.ieee.org/document/8850096
python代码:https://github.com/zhao62/Deep-Residual-Shrinkage-Networks
引用格式:
M. Zhao, S. Zhong, X. Fu, B. Tang, M. Pecht, Deep residual shrinkage networks for fault diagnosis, IEEE Transactions on Industrial Informatics, vol. 16, no. 7, pp. 4681-4690, 2020.
摘要:本文提出了一种新的深度学习方法,名为深度残差收缩网络(DRSN),来提高深度学习方法从强噪声信号中学习特征的能力,并且取得较高的故障诊断准确率。软阈值化作为非线性层,嵌入到深度神经网络之中,以消除不重要的特征。更进一步地,考虑到软阈值化中的阈值是难以设定的,本文所提出的DRSN采用了一个子网络,来自动地设置这些阈值,从而回避了信号处理领域的专业知识。该方法的有效性通过多种不同噪声下的实验进行了验证。
关键词:深度学习,深度残差网络,故障诊断,软阈值化,振动信号
一.引言
旋转机械在制造业、电力供应、运输业和航天工业都是很重要的。然而,因为这些旋转机械在严酷的工作环境下运行,其机械传动系统不可避免地会遭遇一些故障,并且会导致事故和经济损失。准确的机械传动系统故障诊断,能够利于安排维修计划、延长服役寿命和确保人身安全[1]-[3]。
现有的机械传动系统故障诊断算法可分为两类:一类是基于信号分析的方法,另一类是基于机器学习的方法[4]。通常,基于信号分析的故障诊断方法通过检测故障相关的振动成分或者特征频率,来确定故障类型。然而,对于大型旋转机械,其振动信号往往是由许多不同的振动信号混叠而成的,包括齿轮的啮合频率、轴和轴承的旋转频率等。更重要地,当故障处于早期阶段时,故障相关的振动成分往往是比较微弱的,容易被其他的振动成分和谐波所淹没。总而言之,传统基于信号分析的故障诊断方法经常难以检测到故障相关的振动成分和特征频率。
从另一方面来讲,基于机器学习的故障诊断方法,在诊断故障的时候不需要确定故障相关的成分和特征频率。首先,一组统计特征(例如峭度、均方根值、能量、熵)能够被提取来表征健康状态;然后一个分类器(例如多分类支持向量机、单隐含层的神经网络、朴素贝叶斯分类器)能够被训练以诊断故障。然而,所提取的统计特征经常是判别性不足的,难以区分故障,从而导致了较低的诊断准确率。因此,寻找一个判别性强的特征集,是基于机器学习的故障诊断方法所面临的一个长期挑战[5]。
近年来,深度学习方法[6],即包含多个非线性映射层的机器学习方法,成为了基于振动信号进行故障诊断的有力工具。深度学习方法能够自动地从原始振动数据中学习特征,以取代传统的统计特征,获得更高的诊断准确率。许多深度学习方法已经在机械故障诊断领域得到了应用[7]-[14]。例如,Ince等人[7]采用一维卷积神经网络(ConvNet),从电流信号中学习特征,用于实时电机故障诊断。Shao等人[9]采用一种卷积深度置信网络,用于电机轴承的故障诊断。然而,对于传统深度学习方法,参数优化经常是一个困难的任务。误差函数的梯度,在逐层反向传播的过程中,逐渐变得不准确。因此,在输入层附近的一些层的参数不能够很好地被优化。
深度残差网络(ResNet)是ConvNet的一个新颖变种,采用了恒等路径来减轻参数优化的难度[15]。在ResNet中,梯度不仅逐层地反向传播,而且通过恒等路径直接传递到之前的层[16]。由于优越的参数优化能力,ResNet在最近的一些研究中,已经被应用于故障诊断[17]-[20]。例如,Ma等人[17]将一种解调时频特征输入ResNet,应用于不稳定工况下的行星齿轮箱故障诊断。Zhao等人[18]使用ResNet融合多组小波包系数,应用于故障诊断。相较于普通的ConvNet,ResNet的优势在这些论文中已经得到了验证。
从大型旋转机械(例如风电、机床、重型卡车)所采集的振动信号,经常包含着大量的噪声。在处理强噪声振动信号的时候,ResNet的特征学习能力经常会降低。ResNet中的卷积核,其实就是滤波器,在噪声的干扰下,可能不能检测到故障特征。在这种情况下,在输出层所学习到的高层特征,就会判别性不足,不能够准确地进行故障分类。因此,开发新的深度学习方法,应用于强噪声下旋转机械的故障诊断,是十分必要的。
本文提出了两种深度残差收缩网络(DRSNs),即通道间共享阈值的深度残差收缩网络(DRSN-CS)、通道间不同阈值的深度残差收缩网络(DRSN-CW),来提高从强噪振动信号中学习特征的能力,最终提高故障诊断准确率。本文的主要贡献总结如下:
1)软阈值化(也就是一种流行的收缩方程)作为非线性层,被嵌入深度框架之中,以有效地消除噪声相关的特征。
2)采用特殊设计的子网络,来自适应地设置阈值,从而每段振动信号都有着自己独特的一组阈值。
3)在软阈值化中,共考虑了两种阈值,也就是通道间共享的阈值、通道间不同的阈值。这也是所提出方法DRSN-CS和DRSN-CW的名称由来。
本文的剩余部分安排如下。第二部分简要地回顾了经典的深度残差网络,并且详细阐述了所提出的DRSN-CS和DRSN-CW。第三部分进行了实验对比,第四部分进行了总结。
二.深度残差收缩网络的原理
如第一部分所述,作为一种潜在的、能够从强噪声振动信号中学习判别性特征的方法,本研究考虑了深度学习和软阈值化的集成。相对应地,本部分注重于开发ResNet的两个改进变种,即DRSN-CS和DRSN-CW。本节对相关理论背景和必要想法进行了详细介绍。
A. 基本组成
不管是ResNet,还是所提出的DRSN,都有一些基础的组成,和传统ConvNet是相同的,包括卷积层、整流线性单元激活函数、批标准化、全局均值池化、交叉熵误差函数。这些基本组成的概念在下面进行了介绍。
卷积层是使得ConvNet不同于传统全连接神经网络的关键。卷积层能够大量减少所需要训练的参数数量。这是通过用卷积运算,取代矩阵乘法,来实现的。卷积核中的参数,比全连接层中的权重,少得多。更进一步地,当参数较少时,深度学习不容易遭遇过拟合,从而能够在测试集上获得较高的准确率。输入特征图和卷积核之间的卷积运算,附带着加上偏置,能够用公式表示为
y j = y_j= yj= ∑ i ∈ M j x i ∗ k i j + b j \displaystyle\sum_{_i∈M_j} x_i *k_ij+b_j i∈Mj∑xi∗kij+bj
其中, x i x_i xi是输入特征图的第 i i i个通道, y j y_j yj是输出特征图的第 j j j个通道, k k k是卷积核, b b b是偏置, M j M_j Mj是用于计算输出特征图的第 j j j个通道的输入通道的集合[20]。可以通过重复一定次数的卷积运算,来获得输出特征图。
图1展示了卷积的过程。如图1(a)和(b)所示,特征图和卷积核实际上都是三维张量。在本文中,一维振动信号作为输入,所以特征图和卷积核的高度始终都是1。如图1( c)所示,卷积核在输入特征图上滑动,从而获得输出特征图的一个通道。在每个卷积层中,通常有多于一个卷积核,从而输出特征图有多个通道。
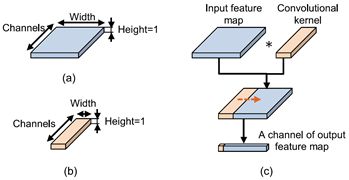
图1 (a)特征图、(b)卷积核和( c)卷积过程示意图
批标准化是一种嵌入到深度学习结构的内部、作为可训练层的一种特征标准化方法。批标准化的目的在于减轻内部协方差漂移的问题,即特征的分布经常在训练过程中持续变化。在这种情况下,所需训练的参数就需要不断地适应变化的特征分布,从而增大了训练的难度。批标准化在第一步对特征进行标准化,获得一个固定的分布(均值为零、标准差为1),然后在训练过程中自适应地调整这个分布。批标准化的计算流程如下:
μ = μ= μ= 1 N b a t c h \frac{1}{N_batch} Nbatch1 ∑ n = 1 N b a t c h x n \sum_{n=1}^{N_batch}x_n ∑n=1Nbatchxn
σ 2 = σ^2= σ2= 1 N b a t c h \frac{1}{N_batch} Nbatch1 ∑ n = 1 N b a t c h ( x n − μ ) 2 \sum_{n=1}^{N_batch} (x_n - μ)^2 ∑n=1Nbatch(xn−μ)2
x ^ n \widehat{x}_n x n = ( x n − μ ) √ ( σ 2 + ϵ ) =\frac{(x_n-μ)}{√(σ^2+ϵ)} =√(σ2+ϵ)(xn−μ)
y n = γ y_n=γ yn=γ x ^ n \widehat{x}_n x n+β
其中, x n x_n xn和 y n y_n yn分别表示一个小批量中第 n n n个样本的输入特征和输出特征, γ γ γ和 β β β分别表示尺度化和平移分布的两个可训练参数, ϵ ϵ ϵ是一个接近于零的正数。
激活函数通常是神经网络中必不可少的一部分,一般是用来实现非线性变换的。在过去的几十年中,很多种激活函数被提出来,例如Sigmoid、Tanh和ReLU。其中,ReLU激活函数最近得到了很多关注,这是因为ReLU能够很有效地避免梯度消失的问题。ReLU激活函数的导数要么是1,要么是0,能够在特征在层间传递的时候,帮助控制特征的取值范围大致不变。ReLU激活函数的表达式为
y = m a x ( x , 0 ) y=max(x,0) y=max(x,0)
其中, x x x和 y y y分别表示ReLU激活函数的输入和输出特征。
全局均值池化是从特征图的每个通道计算一个平均值的运算。通常,全局均值池化是在最终输出层之前使用的。全局均值池化可以减少全连接输出层的权重数量,从而降低深度神经网络遭遇过拟合的风险。全局均值池化还可以解决平移变化问题,从而深度神经网络所学习得到的特征,不会受到故障冲击在时域波形中位置变化的影响。
交叉熵损失函数通常作为多分类问题的目标函数,朝着最小的方向进行优化。相较于传统的均方差损失函数,交叉熵损失函数经常能够提供更快的训练速度。这是因为,交叉熵损失函数对于权重的梯度,相较于均方差损失函数,不容易减弱到零。为了计算交叉熵损失函数,首先要用softmax函数将特征转换到零一区间,表示如下:
y j = e x j ∑ i = 1 N c l a s s e x i y_j= \frac{e^{x_j }}{\sum_{i=1}^{N_class}e^{x_i } } yj=∑i=1Nclassexiexj
其中, x x x和 y y y分别表示softmax函数的输入和输出特征, i i i和 j j j表示输出层神经元的序号, N c l a s s N_class Nclass表示类别数量。此处, y j y_j yj被视为一个样本归属于第 j j j个类别的预测概率。然后,每个样本的交叉熵误差函数表示如下:
E = − ∑ j = 1 N c l a s s t j l o g ( y j ) E=-∑_{j=1}^{N_class} t_j log(y_j) E=−∑j=1Nclasstjlog(yj)
其中, t t t是目标输出, t j t_j tj是一个样本归属于第 j j j个类别的实际概率。在计算完交叉熵误差之后,梯度下降算法被用于优化参数。在一定迭代次数之后,深度神经网络就可以得到充分训练。
B. 经典ResNet的结构
ResNet是一种新兴的深度学习方法,在近年来受到了广泛的关注[15]。残差构建模块是基本的组成部分。如图2(a)所示,一个残差构建模块包含了两个批标准化、两个整流线性单元、两个卷积层和一个恒等路径。恒等路径是让ResNet优于ConvNet的关键。交叉熵损失函数的梯度,在普通的ConvNet中,是逐层反向传播的。当使用恒等路径的时候,梯度能够更有效地流回前面的层,从而参数能够得到更有效的更新。图2(b)-( c)展示了两种残差构建模块,能够输出不同尺寸的特征图。在这里,减小输出特征图尺寸的原因是为了减小后续层的运算量;增加通道数的原因在于,方便将不同的特征构造成强判别性特征。图2(d)展示了ResNet的整体框架,包括一个输入层、一个卷积层、一定数量的残差构建模块、一个批标准化、一个ReLU激活函数、一个全局均值池化和一个全连接输出层。同时,本研究将ResNet作为基准,以进行进一步改进。
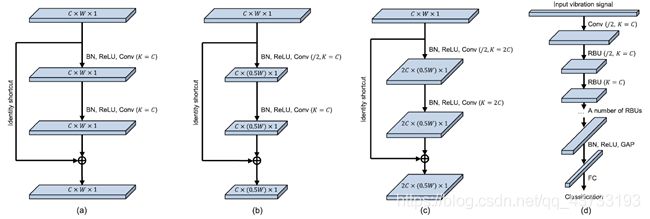
图2 三种残差构建模块,包括(a)第一种残差模块,其输入特征图的尺寸=输出特征图的尺寸,(b)第二种残差模块,其输出特征图的宽度减半,( c)第三种残差模块,其输出特征图的宽度减半、通道数翻倍,(d) ResNet的整体框架,其中/2表示卷积核的移动步长为2,C、W和1分别表示特征图的通道数、宽度和高度,K是卷积核的个数
C. DRSN的基本结构设计
这一小节首先介绍了提出DRSNs的原始动机,然后详细介绍了所提出的两种DRSNs(即DRSN-CS和DRSN-CW)的结构。
1) 理论背景
在过去的20年中,软阈值化经常被用作信号降噪算法的关键步骤。通常,信号被转换到一个域。在这个域中,接近于零的特征是不重要的。然后,软阈值化将这些接近于零的特征置为零。例如,小波阈值化是一种经典的信号降噪算法,通常包括三个步骤:小波分解、软阈值化和小波重构。为了保证信号降噪的效果,小波阈值化的一个关键任务是设计一个滤波器。这个滤波器能够将有用信息转换成比较大的特征,将噪声相关的信息转换成接近于零的特征。然而,设计这样的滤波器需要大量信号处理方面的专业知识,经常是非常困难的。深度学习提供了一种解决这个问题的新思路。这些滤波器可以通过反向传播算法自动优化得到,而不是由专家进行设计。因此,软阈值化和深度学习的结合是一种有效地消除噪声信息和获取强判别性特征的方式。软阈值化的方程表示如下:
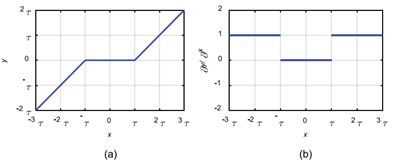
y = y= y= { x − τ x > τ 0 − τ ≤ x ≤ τ x + τ x < − τ \begin{cases}x-τ&x>τ\\0&-τ≤x≤τ\\x+τ&x<-τ\end{cases} ⎩⎪⎨⎪⎧x−τ0x+τx>τ−τ≤x≤τx<−τ
其中 x x x是输入特征, y y y是输出特征, τ τ τ是阈值(即一个正数)。软阈值化将接近于零的特征直接置为零,而不是像ReLU那样,将负的特征置为零,所以负的、有用的特征能够被保留下来。
软阈值化的过程如图3(a)所示。可以看出,软阈值化的输出对于输入的导数要么是1,要么是0,所以在避免梯度消失和梯度爆炸的问题上,也是有效的(图3(b))。其偏导数表示为:
∂ y ∂ x = \frac{∂y}{∂x}= ∂x∂y= { 1 x > τ 0 − τ ≤ x ≤ τ 1 x < − τ \begin{cases}1&x>τ\\0&-τ≤x≤τ\\1&x<-τ\end{cases} ⎩⎪⎨⎪⎧101x>τ−τ≤x≤τx<−τ
在传统的信号降噪算法中,经常难以给阈值设置一个合适的值。同时,对于不同的样本,最优的阈值往往是不同的。针对这个问题,DRSNs的阈值,是在深度神经网络中自动确定的,从而避免了人工的操作。在DRSNs中,这种设置阈值的方式,在后续文中进行了介绍。
2) DRSN-CS的结构
本文所提出的DRSN-CS,是ResNet的一个变种,使用了软阈值化来消除与噪声相关的特征。软阈值化作为非线性层嵌入到残差构建模块之中。更重要地,阈值是在残差构建模块中自动学习得到的。

图4 (a)通道间共享阈值的残差模块,(b)DRSN-CS,(c)通道间不同阈值的残差模块,(d)DRSN-CW
如图4(a)所示,名为“通道间共享阈值的残差收缩构建模块(RSBU-CS)”,与图2(a)中残差构建模块是不同的,有一个特殊模块来估计软阈值化所需要的阈值。在这个特殊模块中,全局均值池化被应用在特征图的绝对值上面,来获得一维向量。然后,这个一维向量被输入到一个两层的全连接网络中,来获得一个尺度化参数。Sigmoid函数将这个尺度化参数规整到0和1之间,表示为
α = 1 1 + e − z α=\frac{1}{1+e^{-z} } α=1+e−z1
其中, z z z是RSBU-CS中两层全连接层的输出, α α α是对应的尺度化参数。然后,这个尺度化参数,乘以特征图的绝对值的平均值,作为阈值。这个安排是由于软阈值化的阈值不仅需要为正数,而且不能太大。如果阈值大于特征图内绝对值最大的特征,那么软阈值化的输出就会全部为0。作为总结,RSBU-CS中的阈值表示为
τ = α ⋅ τ=α· τ=α⋅ a v e r a g e i , j , c \underset{i,j,c}{average} i,j,caverage ∣ x i , j , c ∣ |x_{i,j,c} | ∣xi,j,c∣
其中, τ τ τ是阈值, i , j i,j i,j和 c c c分别表示特征图x的宽、长和通道的序号。这样的话,就可以把阈值控制在一个合适的范围内,不会使输出特征全部为零。如图2(b)和( c)所示,步长为2和通道数量翻倍的RSBU-CS可以通过相似方式进行构建。
本文所提出DRSN-CS的结构简图如图4(b)所示,和图2(d)中经典ResNet是相似的。唯一的区别在于,RSBU-CS替换了普通的残差构建模块。一定数量的RSBU-CS被堆叠起来,从而噪声相关的特征被逐渐削减。另一个优势在于,阈值是自动学习得到的,而不是由专家手工设置的,所以在实施DRSN-CS的时候,不需要信号处理领域的专业知识。
3) DRSN-CW的结构
本文所提出的DRSN-CW是ResNet的另一个变种。与DRSN-CS的区别在于,特征图的每个通道有着自己独立的阈值。通道间不同阈值的残差模块(RSBU-CW)如图4( c)所示。特征图首先被压缩成了一个一维向量,并且输入到一个两层的全连接层中。全连接层的第二层有多于一个神经元,并且神经元的个数等于输入特征图的通道数。全连接层的输出被转换到0和1之间,其公式如下:
α c = 1 1 + e − z c α_c=\frac{1}{1+e^{-z_c} } αc=1+e−zc1
其中 z c z_c zc是第 c c c个神经元处的特征, α c α_c αc是第 c c c个尺度化参数。然后,阈值的计算公式如下:
τ c = α c ⋅ τ_c=α_c· τc=αc⋅ a v e r a g e i , j \underset{i,j}{average} i,javerage ∣ x i , j , c ∣ |x_{i,j,c} | ∣xi,j,c∣
其中 τ c τ_c τc是特征图的第 c c c个通道的阈值, i , j i,j i,j和 c c c分别表示特征图x的宽、长和通道的序号。与DRSN-CS相似,阈值始终是正数,并且被保持在一个合理范围内,从而防止输出特征都是零的情况。
DRSN-CW的整体框架如图4(d)所示。一定数量的DRSN-CW模块被堆积起来,从而学习到判别性特征。其中,软阈值化作为收缩函数,用于非线性变换,来消除噪声相关的信息。
三.实验结果
本文所开发的DRSNs是采用TensorFlow 1.0实现的。这是Google发布的一个机器学习工具包,可以在图形处理单元(Graphic Processing Unit,GPU)上加速运算。实验在配置了i7-6700中央处理器和英伟达GeForce GTX 1070 GPU的计算机上进行。本节对实验结果进行了讨论。
A. 实验数据集
如图5所示,实验数据是从动力传动诊断模拟器采集的。该模拟器主要是由电机、两级行星齿轮箱、两级定轴齿轮箱和可编程磁粉制动器组成的。在行星齿轮箱的输入侧,安装加速度传感器。振动信号的采集频率为12800 Hz。如表1所示,本文考虑了行星齿轮箱的8种健康状态,包括1种健康状态、3种轴承故障和4种齿轮故障。

图5 用于数据采集的动力传动诊断模拟器
表1 行星齿轮箱的八种健康状态
| 类别 | 描述 | 标签 |
|---|---|---|
| 1 | 轴承和齿轮均无故障 | H |
| 2 | 滚动轴承内圈故障 | F1 |
| 3 | 滚动轴承外圈故障 | F2 |
| 4 | 滚动轴承滚动体故障 | F3 |
| 5 | 齿轮齿根裂纹故障 | F4 |
| 6 | 齿轮齿面点蚀故障 | F5 |
| 7 | 齿轮断齿故障 | F6 |
| 8 | 齿轮缺齿故障 | F7 |
对于每种健康状况,考虑了三种不同转速(20、30和40Hz)和三种扭转载荷(1、6和18lb·ft)。在每种特定转速和扭转载荷下,采集了400个样本,使每种健康状态共有3×3×400 =3600个样本。每个样本为时间长度为0.16s的振动信号,有2048个数据点。值得注意的是,这种短信号使故障诊断任务更具挑战性,从而验证所提出的DRSNs的有效性。在实际应用中,可以使用具有更多数据点的长信号。为了验证所提出的DRSNs在不同背景噪声下机械故障诊断的有效性,在每个信号中分别加入高斯白噪声、拉普拉斯噪声和粉红噪声,得到5到-5db信噪比的样本。具体地说,对原始振动信号进行噪声叠加,然后在深度学习模型的训练过程中保持噪声不变。值得注意的是,每个噪声都是独立产生的,因此对于每个振动信号所添加的噪声是不同的。
B. 超参数设置
本文在10折交叉验证框架下进行了实验。具体地,数据集被平均划分为10个子集;每次实验采用1个子集作为测试集,另外9个子集作为训练集;实验重复10次,使每个子集都有一次作为测试集的机会。此外,本文还对所提出的DRSNs中超参数的初始化和选择作了详细介绍。
结构相关的超参数是用来定义神经网络结构的,包括层数、卷积核数、卷积核大小等。由于如何设置这些超参数还没有达成学界共识,本文根据广泛的建议[18]-[20]来设置它们。结构相关的超参数汇总在表2中。CBU是指卷积构造单元,它与RBU的不同之处在于CBU没有使用恒等连接。括号中的第一个和第二个数字分别是指卷积核的数量和宽度。一些括号中的“/2”表示特征图的宽度是通过以2的步长移动卷积核来减小的。不同层中特征图的输出尺寸显示在表2的第二列中;它们要么是通道×宽度×高度的三维形式,要么是向量的一维形式。三维特征图在全局均值池化层之后缩减成一维向量。最后,全连接输出层有8个神经元,等于所考虑类别的数量(即1种健康状态+7种故障状态)。
表2 ConvNet、ResNet、DRSN-CS和DRSN-CW的结构相关的超参数
| 模块数量 | 输出尺寸 | ConvNet | ResNet | DRSN-CS | DRSN-CW |
|---|---|---|---|---|---|
| 1 | 1 × 2048 × 1 | Input | Input | Input | Input |
| 1 | 4 × 1024 × 1 | Conv(4, 3, /2) | Conv(4, 3, /2) | Conv(4, 3, /2) | Conv(4, 3, /2) |
| 1 | 4 × 512 × 1 | CBU(4, 3, /2) | RBU(4, 3, /2) | RSBU-CS(4, 3, /2) | RSBU-CW(4, 3, /2) |
| 3 | 4 × 512 × 1 | CBU(4, 3) | RBU(4, 3) | RSBU-CS(4, 3) | RSBU-CW(4, 3) |
| 1 | 8 × 256 × 1 | CBU(8, 3, /2) | RBU(8, 3, /2) | RSBU-CS(8, 3, /2) | RSBU-CW(8, 3, /2) |
| 3 | 8 × 256 × 1 | CBU(8, 3) | RBU(8, 3) | RSBU-CS(8, 3) | RSBU-CW(8, 3) |
| 1 | 16 × 128 × 1 | CBU(16, 3, /2) | RBU(16, 3, /2) | RSBU-CS(16, 3, /2) | RSBU-CW(16, 3, /2) |
| 3 | 16 × 128 × 1 | CBU(16, 3) | RBU(16, 3) | RSBU-CS(16, 3) | RSBU-CW(16, 3) |
| 1 | 16 | BN, ReLU, GAP | BN, ReLU, GAP | BN, ReLU, GAP | BN, ReLU, GAP |
| 1 | 8 | FC | FC | FC | FC |
优化相关的超参数是用来定义训练过程的。前40个周期的学习率为0.1,之后40个周期的学习率为0.01,最后20个周期的学习率为0.001,这样就可以在开始时以较大的步长更新参数,在结束时微调参数,这遵循了[20]中的设置。动量是一种使用上一步的更新步长来加速训练的策略。根据[15]的建议,动量系数设置为0.9。L2正则化用于减少过拟合的影响,并产生更高的测试精度[6]。L2正则化在目标函数中加入一个惩罚项,使权重趋于零。这样,权值的绝对值就不太可能被训练成非常大的数字,在处理相似的输入时,深度神经网络的输出与权值相乘后也不会有很大的差距。惩罚项的系数被设置为0.0001,这与经典ResNet保持了一致[15]。小批量是指一组随机选择的样本,这些样本在一起被输入到深度学习模型中。与每次输入一个样本的情况相比,可以减少时间消耗。为了与[20]保持一致,批量的大小被设置为128。
C. 与ConvNet、ResNet的实验比较
在不同噪声类型和不同的信噪比情况下的ConvNet、ResNet、DRSN-CS和DRSN-CW的详细实验结果如图6-8所示。图6-8中准确率的平均值如表3所示。此外,无人工添加噪声情况下的准确率见表4,模型优化的时间消耗见表5。
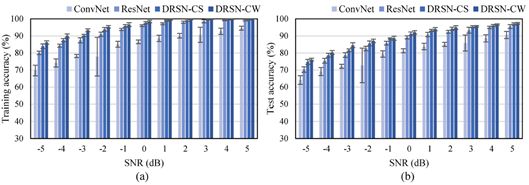
图6 ConvNet、ResNet、DRSN-CS和DRSN-CW在高斯噪声下故障诊断的(a)训练准确率和(b)测试准确率
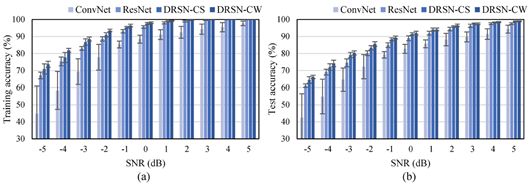
图7 ConvNet、ResNet、DRSN-CS和DRSN-CW在拉普拉斯噪声下故障诊断的(a)训练准确率和(b)测试准确率
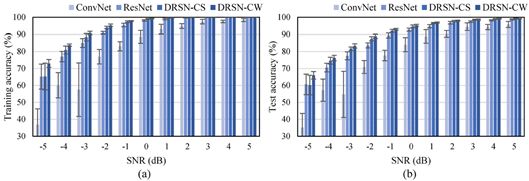
图8 ConvNet、ResNet、DRSN-CS和DRSN-CW在粉红噪声下故障诊断的(a)训练准确率和(b)测试准确率
表3 图6-8中实验结果的平均准确率
| 方法 | 训练准确率 | 测试准确率 |
|---|---|---|
| ConvNet | 82.06 ± 4.29 | 77.62 ± 4.22 |
| ResNet | 91.96 ± 1.05 | 86.25 ± 1.34 |
| DRSN-CS | 93.61 ± 0.98 | 88.55 ± 1.02 |
| DRSN-CW | 94.84 ± 0.55 | 89.57 ± 0.87 |
表4 无人工添加噪声情况下的平均准确率
| 方法 | 训练准确率 | 测试准确率 |
|---|---|---|
| ConvNet | 99.79 ± 0.86 | 96.67 ± 1.60 |
| ResNet | 99.99 ± 0.01 | 99.54 ± 0.24 |
| DRSN-CS | 100.00 ± 0.01 | 99.65 ± 0.08 |
| DRSN-CW | 100.00 ± 0.00 | 99.70 ± 0.16 |
表5 所对比方法的运算时间
| 方法 | 时间 |
|---|---|
| ConvNet | 961.81 |
| ResNet | 978.04 |
| DRSN-CS | 1585.33 |
| DRSN-CW | 1511.11 |
本文采用了一种非线性无监督降维方法,即t-分布随机邻域嵌入[26],在二维空间中可视化全局均值池化层的高级特征。尽管由于降维过程中的信息丢失,二维空间中的可视化存在一定的误差,但是二维可视化的目的是提供一个直观的概念,来判断这些高级特征是否具有区分性。如图9(a)和(b)所示,在经典的ConvNet和ResNet中,不同健康状况下的测试样本高度混合在一起。一些故障类别(如F6)的样本分布在几个不同的区域,这是因为振动信号是在若干不同的工作条件下采集的,具有差异较大的特征。
ConvNet和ResNet无法将它们投影到同一区域。相比之下,如图9( c)和(d)所示,在DRSN-CS和DRSN-CW中,相同类别的样本大多集中在同一区域,并且不同类别的样本基本上是互相远离的。
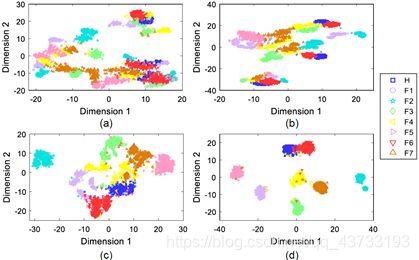
图9 当SNR=5dB时,测试样本在全局均值池化层高维特征的二维可视化:(a)ConvNet,(b)ResNet,( c)DRSN-CS和(d)DRSN-CW
所涉及深度学习方法的训练和测试误差如图10所示。ResNet的训练和测试误差都明显低于ConvNet,这验证了恒等连接的使用有助于参数优化,得到更精确的训练模型。更重要地是,本文所提出的DRSN-CS和DRSN-CW比经典的ResNet具有更低的训练和测试误差。其原因在于,在深层结构中采用软阈值化作为收缩函数,可以减少噪声相关的特征,从而使最后一层的高级特征具有更强的判别能力。

图10 当信噪比=5dB时的训练和测试误差:(a)ConvNet、(b)ResNet、( c)DRSN-CS和(d)DRSN-CW
D. DRSN-CS与DRSN-CW的比较
如表3所示,相较于DRSN-CS,DRSN-CW的平均训练准确率和测试准确率分别提高了1.23%和1.02%。如图9( c)和(d)所示,一些类别对(例如:H与F4、H与F6、F4与F7)在DRSN-CS中发生了严重重叠,而只有一个类别对(H与F6)在DRSN-CW中具有一定程度的重叠。换句话说,DRSN-CW中的类别比DRSN-CS中的类别更加可分离。此外,如图10( c)和(d)所示,DRSN-CW的测试误差(即约0.07)降低到了明显低于DRSN-CS的水平(即约0.11)。
与DRSN-CS相比,DRSN-CW具有更高精度的一个直接原因是:特征图的不同通道通常包含不同数量的噪声信息。因此,DRSN-CW能够采用不同的阈值来进行不同通道的特征收缩,比DRSN-CS更加灵活(其阈值应用于所有通道)。结果表明,DRSN-CW比DRSN-CS能更有效地消除噪声相关信息,并能获得更高的准确率。
DRSN-CS和DRSN-CW的计算时间总结在表5中。可以观察到,DRSN-CS比DRSN-CW花费了更多的时间,这是因为DRSN-CS在每个构建单元中比DRSN-CW多了一个计算步骤(即平均操作)[参见图4(a)和( c)]。在未来,DRSN-CS和DRSN-CW的体系结构需要进一步优化以减少计算时间。
四.结论
在机械故障诊断任务中,需要加强深度学习方法从强噪声振动信号中学习特征的能力,这是一项重要的任务。本文提出了两种新的深度学习方法,即DRSN-CS和DRSN-CW。这两种方法将软阈值化作为可训练的收缩函数嵌入到深层网络结构中,将不重要的特征置为零,从而使学习到的高层特征具有更强的判别性能。阈值是使用嵌入的模块(即专门设计的子网)设置的,因此不需要信号处理方面的专业知识。
通过与传统深度学习方法的对比实验,验证了DRSNs在提高故障诊断准确率方面的有效性。本文所提出的DRSN-CS和DRSN-CW的平均测试准确率,相较于经典的ConvNet分别提高了10.93%和11.95%;相较于经典的ResNet分别提高了2.30%和3.32%。因此,在深度学习方法中引入软阈值化作为可训练的收缩函数,可以有效提高对强噪振动信号的特征学习能力。
就总体平均测试准确率而言,DRSN-CW在性能上比DRSN-CS稍有提高(1.02%),这是因为特征图的不同通道通常含有不同规模的噪声特征。DRSN-CW允许特征图的每个通道具有自己的阈值,这比DRSN-CS(特征图的所有通道使用相同的阈值)更加灵活。结果表明,DRSN-CW比DRSN-CS具有更强的特征学习能力和更高的故障诊断性能。
本文所提出的DRSNs不仅适用于基于振动信号的故障诊断,而且能够用于众多领域、各种含噪信号(如声音信号、视觉信号和电流信号)的模式识别任务。
参考文献
[1] X. Jin, F. Cheng, Y. Peng, W. Qiao, and L. Qu, “Drivetrain gearbox fault diagnosis: Vibration- and current-based approaches,” IEEE Ind. Electron. Mag., vol. 24, no. 6, pp. 56–66, 2018.
[2] Y. Wang, P.W. Tse, B. Tang, Y. Qin, L. Deng, and T. Huang, “Kurtogram manifold learning and its application to rolling bearing weak signal detection,” Measurement, vol. 127, pp. 533–545, 2018.
[3] F. Cong, J. Chen, G. Dong, and M. Pecht, “Vibration model of rolling element bearings in a rotor-bearing system for fault diagnosis,” J. Sound Vib., vol. 332, no. 8, pp. 2081–2097, 2013.
[4] Y. Lei, J. Lin, M. J. Zuo, and Z. He, “Condition monitoring and fault diagnosis of planetary gearboxes: A review,” Measurement, vol. 48, pp. 292–305, 2014.
[5] R. Liu, B. Yang, E. Zio, and X. Chen, “Artificial intelligence for fault diagnosis of rotating machinery: A review,” Mech. Syst. Signal Process., vol. 108, pp. 33–47, 2018.
[6] I. Goodfellow, Y. Bengio, and A. Courville, Deep Learning. Cambridge, MA, USA: MIT Press, 2016.
[7] T. Ince, S. Kiranyaz, L. Eren, M. Askar, and M. Gabbouj, “Real-time motor fault detection by 1-D convolutional neural networks,” IEEE Trans. Ind. Electron., vol. 63, no. 11, pp. 7067–7075, 2016.
[8] W. Sun, R. Zhao, R. Yan, S. Shao, and X. Chen, “Convolutional discriminative feature learning for induction motor fault diagnosis,” IEEE Trans. Ind. Inform., vol. 13, no. 3, pp. 1350–1359, 2017.
[9] H. Shao, H. Jiang, H. Zhang, and T. Liang, “Electric locomotive bearing fault diagnosis using a novel convolutional deep belief network,” IEEE Trans. Ind. Electron., vol. 65, no. 3, pp. 2727–2736, 2018.
[10] R. Liu, G. Meng, B. Yang, C. Sun, and X. Chen, “Dislocated time series convolutional neural architecture: An intelligent fault diagnosis approach for electric machine,” IEEE Trans. Ind. Inform., vol. 13, no. 3, pp. 1310–1320, 2017.
[11] C. Sun, M. Ma, Z. Zhao, and X. Chen, “Sparse deep stacking network for fault diagnosis of motor,” IEEE Trans. Ind. Inform., vol. 14, no. 7, pp. 3261–3270, 2018.
[12] R. Razavi-Far, E. Hallaji, M. Farajzadeh-Zanjani, M. Saif, S. H. Kia, H. Henao, and G. Capolino, “Information fusion and semi-supervised deep learning scheme for diagnosing gear faults in induction machine systems,” IEEE Trans. Ind. Electron., vol. 66, no. 8, pp. 6331–6342 , 2019.
[13] R. Chen, X. Huang, L. Yang, X. Xu, X. Zhang, and Y. Zhang, “Intelligent fault diagnosis method of planetary gearboxes based on convolution neural network and discrete wavelet transform,” Comput. Ind., vol. 106, pp. 48–59, 2019.
[14] Y. Han, B. Tang, and L. Deng, “An enhanced convolutional neural network with enlarged receptive fields for fault diagnosis of planetary gearboxes,” Comput. Ind., vol. 107, pp. 50–58, 2019.
[15] K. He, X. Zhang, S. Ren, and J. Sun, “Deep residual learning for image recognition,” in Proc. IEEE Conf. Comput. Vision Pattern Recognit., Seattle, WA, USA, Jun. 27–30, 2016, pp. 770–778.
[16] K. He, X. Zhang, S. Ren, and J. Sun, “Identity mappings in deep residual networks,” in Computer Vision—ECCV 2016 (Lecture Notes in Computer Science 9908), B. Leibe, J. Matas, N. Sebe, and M. Welling, Eds., Cham, Switzerland: Springer, 2016, pp. 630–645.
[17] S. Ma, F. Chu, and Q. Han, “Deep residual learning with demodulated time-frequency features for fault diagnosis of planetary gearbox under nonstationary running conditions,” Mech. Syst. Signal Process., vol. 127, pp. 190–201, 2019.
[18] M. Zhao, M. Kang, B. Tang, and M. Pecht, “Multiple wavelet coefficients fusion in deep residual networks for fault diagnosis,” IEEE Trans. Ind. Electron., vol. 66, no. 6, pp. 4696–4706, 2019.
[19] W. Zhang, X. Li, and Q. Ding, “Deep residual learning-based fault diagnosis method for rotating machinery,” ISA Transactions, to be published.
[20] M. Zhao, M. Kang, B. Tang, and M. Pecht, “Deep residual networks with dynamically weighted wavelet coefficients for fault diagnosis of planetary gearboxes,” IEEE Trans. Ind. Electron., vol. 65, no. 5, pp. 4290 –4300, 2018.
[21] S. Ioffe and C. Szegedy, “Batch normalization: Accelerating deep network training by reducing internal covariate shift,” in Proc. 32nd Int. Conf. Mach. Learn., Lille, France, Jul. 7–9, 2015, pp. 448–456.
[22] M. Lin, Q. Chen, and S. Yan, “Network in network,” in Proc. Int. Conf. Learn. Represen., Banff, Canada, Apr. 14–16, 2014.
[23] D. L. Donoho, “De-noising by soft-thresholding,” IEEE Trans. Inf. Theory, vol. 41, no. 3, pp. 613–627, 1995.
[24] K. Isogawa, T. Ida, T. Shiodera, and T. Takeguchi, “Deep shrinkage convolutional neural network for adaptive noise reduction,” IEEE Signal Process. Lett., vol. 25, no. 2, pp. 224–228, 2018.
[25] J. Hu, L. Shen, and G. Sun, “Squeeze-and-excitation networks,” in Proc. IEEE Conf. Comput. Vision Pattern Recognit., Salt Lake City, UT, USA, Jun. 18–23, 2018, pp. 7132–7141.
[26] L. J. P. van der Maaten and G. E. Hinton, “Visualizing high-dimensional data using t-SNE,” J. Mach. Learn. Res., vol. 9, pp. 2579–2605, 2008.