目标检测（一）—— SSD（single shot multibox detection）

1 Inference

Single shot指明了SSD算法属于one-stage方法，MultiBox指明了SSD是多框预测。

SSD是一种one-stage方法，其主要思路是均匀地在图片的不同位置进行密集抽样，抽样时可以采用不同尺度和长宽比，然后利用CNN提取特征后直接进行分类与回归，整个过程只需要一步，所以其优势是速度快。

---

2 基本结构与设计理念

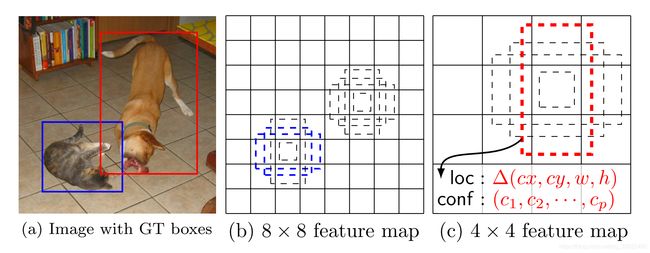
2.1 default box & feature map cell

• feature map cell 就是将 feature map 切分成 $8\times 8$ 或者 $4\times 4$ 之后的一个个格子；
• 而 default box 就是每一个格子上，一系列固定大小的 box，即图中虚线所形成的一系列 boxes。

2.2 Model

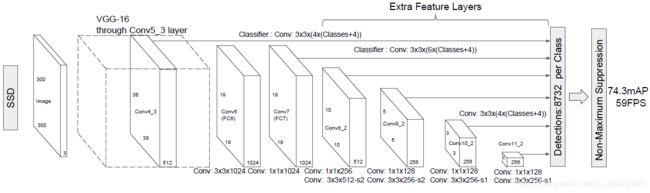
SSD 是基于一个前向传播 CNN 网络，产生一系列 固定大小（fixed-size） 的 bounding boxes，以及每一个 box 中包含物体实例的可能性，即 score。之后，进行一个 非极大值抑制（Non-maximum suppression） 得到最终的 predictions。

---

SSD 300中输入图像的大小是300x300，特征提取部分使用了VGG16的卷积层，并将VGG16的两个全连接层转换成了普通的卷积层（图中conv6和conv7），之后又接了多个卷积（conv8_1，conv8_2，conv9_1，conv9_2，conv10_1，conv10_2），最后用一个Global Average Pool来变成1x1的输出（conv11_2）。

---

2.3 设计理念

2.3.1 多尺度特征预测

• 采用多尺度特征图用于分类和位置回归：
  SSD将conv4_3、conv7、conv8_2、conv9_2、conv10_2、conv11_2都连接到了最后的检测、分类层做回归。

  CNN网络一般前面的特征图比较大，后面会逐渐采用stride=2的卷积或者pool来降低特征图大小。如下图所示，一个比较大的特征图和一个比较小的特征图，它们都用来做检测。这样做的好处是比较大的特征图来用来检测相对较小的目标，而小的特征图负责检测大目标，8x8的特征图可以划分更多的单元，但是其每个单元的先验框尺度比较小，可检测相对较小的目标。
  

---

2.2.2 采用卷积进行检测

SSD直接采用卷积对不同的特征图来进行提取检测结果。对于形状为 $m\times n\times p$的特征图，只需要采用$3\times 3\times p$ 这样比较小的卷积核得到检测值。

使用一系列 convolutional filters，去产生一系列固定大小的 predictions，
产生的 predictions有以下两种：

• 归属类别的一个得分
• 相对于 default box coordinate 的 shape offsets。

---

2.2.3 Anchor

Anchor的生成：

1. 特征图的每个点都会生成一大一小两个正方形的anchor。 小方形的边长用min_size来表示，大方形的边长用$\sqrt{min\_size\ast max\_size}$来表示(min_size与max_size的值每一层都不同)。
   

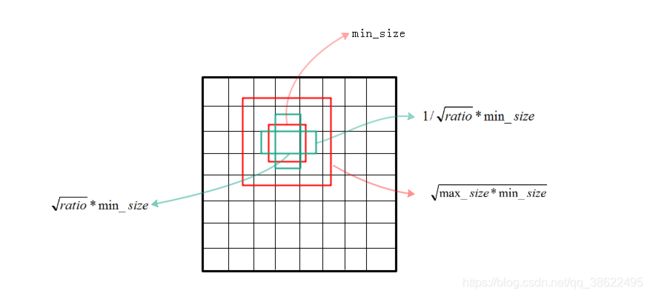
2. 多个长方形的anchor。 长方形anchor的数目在不同层级会有差异，他们的长宽可以用下面的公式来表达，ratio的数目就决定了某层上每一个点对应的长方形anchor的数目：

   $$width=\sqrt{ratio}\ast min\_size$$
   $$length=1/\sqrt{ratio}\ast min\_size$$
   上面的min_size和max_size由下式计算得到，$Smin=0.2，Smax=0.95$，m代表全部用于回归的层数，比如在SSD 300中m就是6。第k层的$min\_size=S_k$，第k层的$max\_size=S_{k+1}$
   

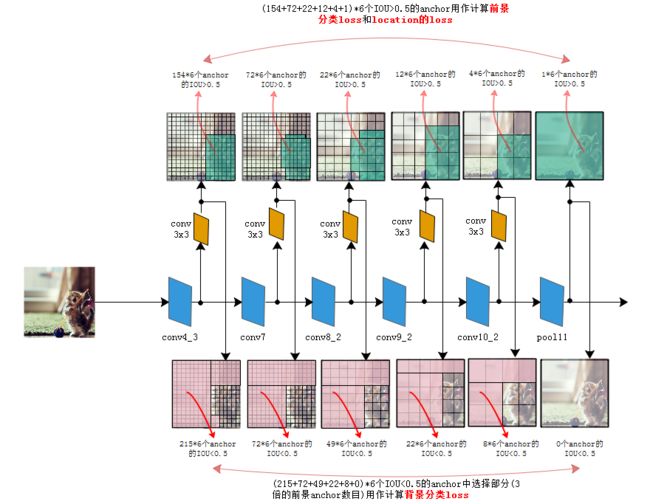
多个层级上的anchor回归：

如图所示，左边较低的层级因为feature map尺寸比较大，anchor覆盖的范围就比较小，远小于ground truth的尺寸，所以这层上所有anchor对应的IOU都比较小；右边较高的层级因为feature map尺寸比较小，anchor覆盖的范围就比较大，远超过ground truth的尺寸，所以IOU也同样比较小；只有图2中间的anchor才有较大的IOU。通过同时对多个层级上的anchor计算IOU，就能找到与ground truth的尺寸、位置最接近（即IOU最大）的一批anchor，在训练时也就能达到最好的准确度。

---

2.2.4 Loss

SSD包含三部分的loss：前景分类的loss、背景分类的loss、位置回归的loss。计算公式如下：

$$L\left(x,c,l,g\right)=\frac{1}{N}\left(L_{conf}(x,c)+\alpha L_{loc}(x,l,g)\right)$$

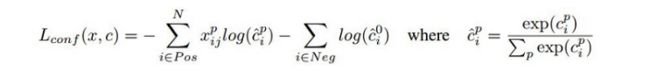
其中：

• $N$ 是与 ground truth box 相匹配的 default boxes 个数

• localization loss（loc） 是 Smooth L1 Loss，用在 $predictbox（l）$ 与 $groundtruthbox（g）$ 参数（即中心坐标位置，width、height）中，回归 bounding boxes 的中心位置，以及 width、height

• confidence loss（conf） 是 Softmax Loss，输入为每一类的置信度 $c$

• 权重项 $\alpha$，设置为 1

$L_{conf}(x,c)$是前景的分类loss和背景的分类loss的和，$L_{loc}(x,l,g)$是所有用于前景分类的anchor的位置坐标的回归loss。

N表示被选择用作前景分类的anchor的数目，在源码中把$IOU>0.5$的anchor都用于前景分类，在$IOU<0.5$的anchor中选择部分用作背景分类。只选择部分的原因是背景anchor的数目一般远远大于前景anchor，如果都选为背景，就会弱化前景loss的值，造成定位不准确。

在作者源码中背景分类的anchor数目定为前景分类anchor数的三倍来保持它们的平衡。$x_{ij}^p$是第i个anchor对第j个ground truth的分类值，$x_{ij}^p$不是1就是0。

$L_{loc}(x,l,g)$位置回归仍采用Smooth L1方法其中的α是前景loss和背景loss的调节比例，论文中$\alpha =1$。

2.2.4.1 回归预测

$L_{loc}(x,l,g)$:

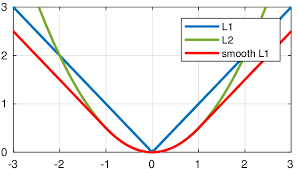
1. 当预测值与目标值相差很大时, 因为梯度里包含了$x^{-t}$，梯度容易爆炸, ，所以SSD使用SmoothL1Loss损失函数。当差值太大时, 原先L2梯度里的$x^{-t}$被替换成了±1, 这样就避免了梯度爆炸, 也就是它更加健壮。

2. 边界框预测时使用了 L1 损失，但这个函数在 0 点处导数不唯一，因此可能会影响收敛。一个常用改进是在 0 点附近使用平方函数使得它更加平滑。它被称之为平滑 L1 损失函数。它通过一个参数 σ 来控制平滑的区域：

   $$\{\begin{array}{cc}{\left(\sigma x\right)}^2/2,& \text{if }x<1/{\sigma }^2\\ |x|-0.5/{\sigma }^2,& \text{otherwise}\end{array}$$

曲线图如下所示：

2.2.4.2 类别预测

$L_{conf}(x,c)$:
$L_{conf}(x,c)$使用了交叉熵损失函数。假设对真实类别 j 的概率预测是 $p_j$，交叉熵损失为 $log(p_j)$。我们可以使用一个被称为关注损失（focal loss）的函数来对之稍微变形。给定正的 $\gamma$ 和 $\alpha$，它的定义如下：
$$-\alpha (1-p_j{)}^{\gamma }\log (p_j)$$
增加 $\gamma$ 可以减小正类预测值比较大时的损失。

2.2.4.3 SSD在6个层级上进行回归

---

3 总结

4 SSD的Gluon实现

4.1 类别预测

• 假设物体有n类，则需要对锚框作n+1个分类,其中类0表示背景。以输入像素为中心输入a个锚框，设高、宽分别为h、w，会有a*h*w个预测结果。
• 使用卷积层的通道来输出类别预测。如果使用全连接层作为输出，可能会导致有过多的模型参数。NIN

类别预测层使用一个保持输入高宽的卷积层，其输出的 (x,y) 像素通道里包含了以输入 (x,y) 像素为中心的所有锚框的类别预测。其输出通道数为 a(n+1)，其中通道 i(n+1) 是第 i 个锚框预测的背景置信度，而通道 i(n+1)+j+1 则是第 i 锚框预测的第 j 类物体的置信度。

def cls_predictor(num_anchors, num_classes):
    return nn.Conv2D(num_anchors * (num_classes + 1), kernel_size=3,
                     padding=1)

定义分类器：
指定 a 和n后，它使用一个填充为 1 的3×3 卷积层。注意到我们使用了较小的卷积窗口，它可能不能覆盖锚框定义的区域。所以我们需要保证前面的卷积层能有效的将较大的锚框区域的特征浓缩到一个 3×3 的窗口里。

4.2 边界框预测

对每个锚框我们需要预测如何将其变换到真实的物体边界框。变换由一个长为 4 的向量来描述，分别表示左下和右上的 x、y 轴坐标偏移。与类别预测类似，这里我们同样使用一个保持高宽的卷积层来输出偏移预测，它有 4a 个输出通道，对于第 i 个锚框，它的偏移预测在 4i 到 4i+3这 4 个通道里。

def bbox_predictor(num_anchors):
    return nn.Conv2D(num_anchors * 4, kernel_size=3, padding=1)

4.3 合成多层的预测输出

SSD 中会在多个尺度上进行预测。由于每个尺度上的输入高宽和锚框的选取不一样，导致其形状各不相同。下面例子构造两个尺度的输入，其中第二个为第一个的高宽减半。然后构造两个类别预测层，其分别对每个输入像素构造 5 个和 3 个锚框。

def forward(x, block):
    block.initialize()
    return block(x)

y1 = forward(nd.zeros((2, 8, 20, 20)), cls_predictor(5, 10))
y2 = forward(nd.zeros((2, 16, 10, 10)), cls_predictor(3, 10))
(y1.shape, y2.shape)

out:((2, 55, 20, 20), (2, 33, 10, 10))

预测的输出格式为（批量大小，通道数，高，宽）。首先将通道，即预测结果，放到最后。因为不同尺度下批量大小保持不变，所以将结果转成二维的（批量大小，高 × 宽 × 通道数）格式，方便之后的拼接。

首先将通道，即预测结果，放到最后。因为不同尺度下批量大小保持不变，所以将结果转成二维的（批量大小，高 × 宽 × 通道数）格式，方便之后的拼接。

def flatten_pred(pred):
    return pred.transpose(axes=(0, 2, 3, 1)).flatten()

拼接就是简单将在维度 1 上合并结果。

def concat_preds(preds):
    return nd.concat(*[flatten_pred(p) for p in preds], dim=1)

concat_preds([y1, y2]).shape
out:(2, 25300)

4.4 减半模块

减半模块将输入高宽减半来得到不同尺度的特征，这是通过步幅 2 的 2×2 最大池化层来完成。我们前面提到因为预测层的窗口为 3，所以我们需要额外卷积层来扩大其作用窗口来有效覆盖锚框区域。为此我们加入两个 3×3 卷积层，每个卷积层后接批量归一化层和 ReLU 激活层。这样，一个尺度上的 3×3 窗口覆盖了上一个尺度上的 10×10 窗口。

def down_sample_blk(num_filters):
    blk = nn.HybridSequential()
    for _ in range(2):
        blk.add(nn.Conv2D(num_filters, kernel_size=3, padding=1),
                nn.BatchNorm(in_channels=num_filters),
                nn.Activation('relu'))
    blk.add(nn.MaxPool2D(2))
    blk.hybridize()
    return blk

forward(nd.zeros((2, 3, 20, 20)), down_sample_blk(10)).shape

out:(2, 10, 10, 10)

4.5 主体网络

主体网络用来从原始图像抽取特征，一般会选择常用的深度卷积神经网络。一般使用了 VGG，大家也常用 ResNet 替代。本小节为了计算简单，我们构造一个小的主体网络。网络中叠加三个减半模块，输出通道数从 16 开始，之后每个模块对其翻倍。

def body_blk():
    blk = nn.HybridSequential()
    for num_filters in [16, 32, 64]:
        blk.add(down_sample_blk(num_filters))
    return blk

forward(nd.zeros((2, 3, 256, 256)), body_blk()).shape

out: (2, 64, 32, 32)

4.6 完整的模型

构建整个模型，这个模型有五个模块，每个模块对输入进行特征抽取，并且预测锚框的类和偏移。第一个模块使用主体网络，第二到四模块使用减半模块，最后一个模块则使用全局的最大池化层来将高宽降到 1。

def get_blk(i):
    if i == 0:
        blk = body_blk()
    elif i == 4:
        blk = nn.GlobalMaxPool2D()
    else:
        blk = down_sample_blk(128)
    return blk

定义每个模块前向计算。它跟之前的卷积神经网络不同在于，不仅输出卷积块的输出，而且还返回在输出上生成的锚框，以及每个锚框的类别预测和偏移预测。

def single_scale_forward(x, blk, size, ratio, cls_predictor, bbox_predictor):
    y = blk(x)
    anchor = contrib.ndarray.MultiBoxPrior(y, sizes=size, ratios=ratio)
    cls_pred = cls_predictor(y)
    bbox_pred = bbox_predictor(y)
    return (y, anchor, cls_pred, bbox_pred)

定义其输出上的锚框如何生成。比例固定成 1、2 和 0.5，但大小上则不同，用于覆盖不同的尺度。

num_anchors = 4
sizes = [[0.2, 0.272], [0.37, 0.447], [0.54, 0.619], [0.71, 0.79],
         [0.88, 0.961]]
ratios = [[1, 2, 0.5]] * 5

4.7完整模型定义

class TinySSD(nn.Block):
    def __init__(self, num_classes, verbose=False, **kwargs):
        super(TinySSD, self).__init__(**kwargs)
        self.num_classes = num_classes
        for i in range(5):
            setattr(self, 'blk_%d' % i, get_blk(i))
            setattr(self, 'cls_%d' % i, cls_predictor(num_anchors,
                                                      num_classes))
            setattr(self, 'bbox_%d' % i, bbox_predictor(num_anchors))

    def forward(self, x):
        anchors, cls_preds, bbox_preds = [None] * 5, [None] * 5, [None] * 5
        for i in range(5):
            x, anchors[i], cls_preds[i], bbox_preds[i] = single_scale_forward(
                x, getattr(self, 'blk_%d' % i), sizes[i], ratios[i],
                getattr(self, 'cls_%d' % i), getattr(self, 'bbox_%d' % i))
        return (nd.concat(*anchors, dim=1),
                concat_preds(cls_preds).reshape(
                    (0, -1, self.num_classes + 1)),
                concat_preds(bbox_preds))

net = TinySSD(num_classes=2, verbose=True)
net.initialize()
x = nd.zeros((2, 3, 256, 256))
anchors, cls_preds, bbox_preds = net(x)

print('output achors:', anchors.shape)
print('output class predictions:', cls_preds.shape)
print('output box predictions:', bbox_preds.shape)


output achors: (1, 5444, 4)
output class predictions: (2, 5444, 3)
output box predictions: (2, 21776)

4.8 训练

4.8.1 读取数据和初始化训练

数据集

batch_size = 32
train_data, test_data = gb.load_data_pikachu(batch_size)
# GPU 实现里要求每张图像至少有三个边界框，我们加上两个标号为 -1 的边界框。
train_data.reshape(label_shape=(3, 5))

模型和训练器的初始化跟之前类似。

ctx = gb.try_gpu()
net = TinySSD(num_classes=2)
net.initialize(init=init.Xavier(), ctx=ctx)
trainer = gluon.Trainer(net.collect_params(),
                        'sgd', {'learning_rate': 0.1, 'wd': 5e-4})

4.8.2 损失和评估函数

4.8.2.1 损失函数

• 每个锚框的类别预测： Softmax 和交叉熵损失
• 正类锚框的偏移预测：L1 损失函数

cls_loss = gloss.SoftmaxCrossEntropyLoss()
bbox_loss = gloss.L1Loss()

def calc_loss(cls_preds, cls_labels, bbox_preds, bbox_labels, bbox_masks):
    cls = cls_loss(cls_preds, cls_labels)
    bbox = bbox_loss(bbox_preds * bbox_masks, bbox_labels * bbox_masks)
    return cls + bbox

4.8.2.2 评估函数

• 分类：沿用之前的分类精度
• 锚框边框：因为使用了 L1 损失，用平均绝对误差评估边框预测的性能。

def cls_metric(cls_preds, cls_labels):
    # 注意这里类别预测结果放在最后一维，argmax 的时候指定使用最后一维。
    return (cls_preds.argmax(axis=-1) == cls_labels).mean().asscalar()

def bbox_metric(bbox_preds, bbox_labels, bbox_masks):
    return (bbox_labels - bbox_preds * bbox_masks).abs().mean().asscalar()

4.8.3 训练模型

for epoch in range(1, 21):
    acc, mae = 0, 0
    train_data.reset()  # 从头读取数据。
    tic = time.time()
    for i, batch in enumerate(train_data):
        # 复制数据到 GPU。
        X = batch.data[0].as_in_context(ctx)
        Y = batch.label[0].as_in_context(ctx)
        with autograd.record():
            # 对每个锚框预测输出。
            anchors, cls_preds, bbox_preds = net(X)
            # 对每个锚框生成标号。
            bbox_labels, bbox_masks, cls_labels = contrib.nd.MultiBoxTarget(
                anchors, Y, cls_preds.transpose(axes=(0, 2, 1)))
            # 计算类别预测和边界框预测损失。
            l = calc_loss(cls_preds, cls_labels,
                             bbox_preds, bbox_labels, bbox_masks)
        # 计算梯度和更新模型。
        l.backward()
        trainer.step(batch_size)
        # 更新类别预测和边界框预测评估。
        acc += cls_metric(cls_preds, cls_labels)
        mae += bbox_metric(bbox_preds, bbox_labels, bbox_masks)
    if epoch % 5 == 0:
        print('epoch %2d, class err %.2e, bbox mae %.2e, time %.1f sec' % (
            epoch, 1 - acc / (i + 1), mae / (i + 1), time.time() - tic))

4.9 预测

在预测阶段，我们希望能把图像里面所有感兴趣的物体找出来。我们首先定义一个图像预处理函数，它对图像进行变换然后转成卷积层需要的四维格式。

def process_image(file_name):
    img = image.imread(file_name)
    data = image.imresize(img, 256, 256).astype('float32')
    return data.transpose((2, 0, 1)).expand_dims(axis=0), img

x, img = process_image('../img/pikachu.jpg')

在预测的时候，我们通过MultiBoxDetection函数来合并预测偏移和锚框得到预测边界框，并使用 NMS 去除重复的预测边界框。

def predict(x):
    anchors, cls_preds, bbox_preds = net(x.as_in_context(ctx))
    cls_probs = cls_preds.softmax().transpose((0, 2, 1))
    out = contrib.nd.MultiBoxDetection(cls_probs, bbox_preds, anchors)
    idx = [i for i, row in enumerate(out[0]) if row[0].asscalar() != -1]
    return out[0, idx]

out = predict(x)

最后我们将预测出置信度超过某个阈值的边框画出来：

gb.set_figsize((5, 5))

def display(img, out, threshold=0.5):
    fig = gb.plt.imshow(img.asnumpy())
    for row in out:
        score = row[1].asscalar()
        if score < threshold:
            continue
        bbox = [row[2:6] * nd.array(img.shape[0:2] * 2, ctx=row.context)]
        gb.show_bboxes(fig.axes, bbox, '%.2f' % score, 'w')

display(img, out, threshold=0.4)

4.10 损失函数

边界框预测时使用了 L1 损失，但这个函数在 0 点处导数不唯一，因此可能会影响收敛。一个常用改进是在 0 点附近使用平方函数使得它更加平滑。它被称之为平滑 L1 损失函数。它通过一个参数 σ 来控制平滑的区域：
KaTeX parse error: No such environment: split at position 7: \begin{̲s̲p̲l̲i̲t̲}̲f(x) = \beg…
当 σ 很大时它类似于 L1 损失，变小时函数更加平滑。

sigmas = [10, 1, 0.5]
lines = ['-', '--', '-.']
x = nd.arange(-2, 2, 0.1)
gb.set_figsize()

for l, s in zip(lines, sigmas):
    y = nd.smooth_l1(x, scalar=s)
    gb.plt.plot(x.asnumpy(), y.asnumpy(), l, label='sigma=%.1f' % s)
gb.plt.legend();

对于类别预测我们使用了交叉熵损失。

def focal_loss(gamma, x):
    return -(1 - x) ** gamma * x.log()

x = nd.arange(0.01, 1, 0.01)
for l, gamma in zip(lines, [0, 1, 5]):
    y = gb.plt.plot(x.asnumpy(), focal_loss(gamma, x).asnumpy(), l,
                    label='gamma=%.1f' % gamma)
gb.plt.legend();

5 目标检测指标MAP

5.1 IOU

loU(交并比)是模型所预测的检测框和真实(ground truth)的检测框的交集和并集之间的比例。

5.2 Precision

• 单个类别
• 单张图像

图像的类别C的Precision=图像正确预测(True Positives)的数量除以在图像这一类的总的目标数量。

$Precesio{n}_C=\frac{N(TruePositives{)}_C}{N(TotalObjects{)}_C}$

5.3 Average Precision

• 单个类别
• m张图像

一个C类的平均精度=在验证集上所有的图像对于类C的精度值的和/有类C这个目标的所有图像的数量。

$AveragePrecisio{n}_C=\frac{\sum Precisio{n}_C}{N(TotalImages{)}_C}$

5.4 Mean Average Precision

• 给定n类
• 每类IOU
• 计算精度
• 计算平均精度
• 除以类的个数n

AP有20个不同的平均精度值。使用这些平均精度值，我们可以轻松的判断任何给定类别的模型的性能。 但难以度量整个模型，所以选用一个单一的数字来表示一个模型的表现(一个度量来统一它们),我们可以取所有类的平均精度值的平均值，即MAP(均值平均精度)。

$MeanAveragePrecision=\frac{\sum AveragePrecisio{n}_C}{N(Classes)}$

6 参考

• 解读SSD目标检测方法
• 论文阅读：SSD: Single Shot MultiBox Detector
• 单发多框检测（SSD）
• 目标检测|SSD原理与实现
• Liu W, Anguelov D, Erhan D, et al. Ssd: Single shot multibox detector[C]//European conference on computer vision. Springer, Cham, 2016: 21-37.

7 下一步工作安排

• 标注乳液泵，制作乳液泵Pascol VOC样本
• 研究SSD源码，跑数据
• 深入了解SSD原理，并修改源码，跑数据。