机器学习实践入门(三):优化算法和参数调节
本文参考自深蓝学院课程,所记录笔记,仅供自学记录使用
优化算法和参数调节
- 网络优化
-
- 基础回顾
-
- 等高线
- 损失函数VS代价函数VS目标函数
- 梯度和步长优化方案
-
- SGD家族
- 学习率 α \alpha α
- 传统SGD算法的缺点
- SGD算法的改进方案
-
- SGD with momenturn(SGDM;动量SGD)
- SGD with NAG
- AdaGrad
- RMSprop
- Adam = SGD-M +RMSprop
- Nadam= Adam + NAG
- 梯度折断
- 小结
- 参数初始化
-
- 初始化方法
-
- 方差缩放
-
- Xavier参数初始化(tanh 、 sigmoid )
- Kamming初始化 (ReLU )
- 数据预处理
-
- 数据输入归一化
-
- 实际建议:
- 归一化
-
- 网络中间层归一化的常用方法
-
- BN(Batch Normalization)
-
- 对于全连接层来说
- 对于卷积层来说
- LN(Layer Normalization)
-
- 对于全连接层来说
- 对于卷积层来说
- 归一化方法总结
- 正则化(防止过拟合)
-
- L1、L2 正则化
-
- L 1 L_1 L1正则、 L 2 L_2 L2正则
- early stop
- dropout
- Data Augmentation
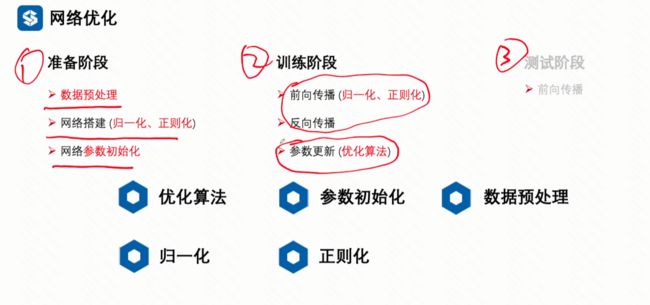
网络优化
基础回顾
等高线
地形图上高度相等的相邻各点所连成的闭合曲线。
➢ 梯度下降的方向与等高线的切线方向垂直;
➢ 鞍点: 从该点出发的一个方向是函数的极大值点,而在另一个方向是函数的极小值点 (一阶导数为0,二阶不为0);导致误判
➢ 极值点: 局部极小 or 全局最小。
损失函数VS代价函数VS目标函数
损失函数 loss function: 单个样本的损失。
L = ( f ( x i ) − y i ) L=(f(x_i)-y_i) L=(f(xi)−yi)
代价函数 cost function: 数据集整体的损失。
L = ∑ i N ( f ( x i ) − y i ) L=\sum_i^N(f(x_i)-y_i) L=∑iN(f(xi)−yi)
目标函数 objective function:经验风险(代价函数)+结构风险
➢经验风险:最小化训练集上的期望损失, 用训练集上的经验分布 P ^ ( X , Y ) \hat{P}(X,Y) P^(X,Y)替代真实的分布 P ( , ) P(, ) P(X,Y) ;(通常用代价函数代替经验风险)
➢ 结构风险:通过正则项防止过拟合现象。
L = ∑ i N ( f ( x i ) − y i ) + Ω ( 正则项 ) L=\sum_i^N(f(x_i)-y_i)+\Omega(正则项) L=∑iN(f(xi)−yi)+Ω(正则项)
一般文献也同城这三项为损失函数
梯度下降法
神经网络参数较多,无法对损失函数直接求解(极值点),需要逐步逼近,达到极值点。

梯度和步长优化方案
本节主要就是讲如何 求解最优的方向(梯度),以及最优步长的
下面是梯度下降算法的一些演变过程
SGD家族
- BGD (batch gradient decent):采用所有样本计算梯度;
- SGD (Stochastic gradient descent):采用单个样本计算梯度;
- MBGD (min-batch gradient decent):采用 个样本计算梯度。
➢ 两个超参:学习率、(batch大小)
➢ 起始点选择(第2小节讲解)
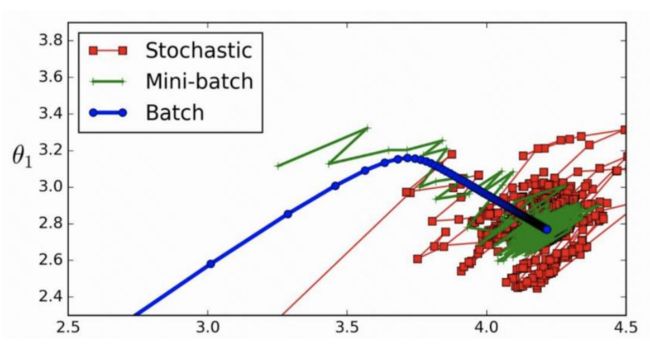
发现:BGD Loss效果似乎最好,训练loss非常平滑,SGD最差,loss不平滑;实际中常用MBGD的方案,因为数据集过大时,不能加载所有数据到内存,而且还要考虑运算速度等,所以平时还是要常用MBGD的方案。
学习率 α \alpha α
➢设置过小,loss下降慢,收敛速度慢;
➢设置过大,loss下降快,无法收敛。
以现有技术来说, α \alpha α的设置 依旧是一个经验值,一般先设置成一个固定大小,比如0.01(一般设置较大),然后查看loss曲线,判断loss下降过慢就增大学习率,反之减小
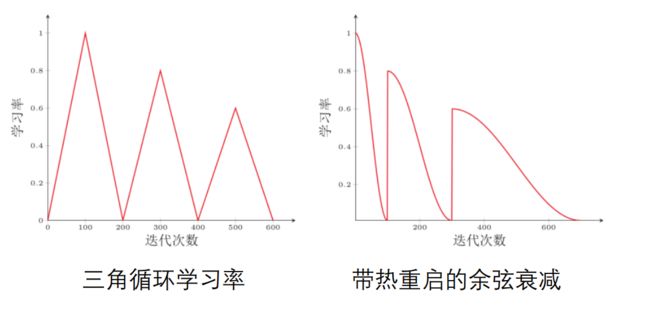
调整学习率的方法
➢ 线性学习率:loss下降稳定,指数级下降趋势;(图像分类常用)
➢ 周期学习率:特定网络下效果较好。(图像分割常用)
Batch Size 批量大小
➢ 越大,随机梯度的方差越小,引入的噪声也越小,训练也越稳定,因此可以设置较大的学习率;
➢ 较小时,需要设置较小的学习率,否则模型会不收敛。
经验:
(1) 越大越好,匹配显存大小
(2) 与学习率成正比关系
传统SGD算法的缺点
缺点
➢ 梯度方向:收敛速度慢,可能在鞍点处震荡;
➢ 学习率:需要手动设定,非最优
SGD算法的改进方案
SGD with momenturn(SGDM;动量SGD)
在梯度下降的过程中加入了惯性,使得在梯度方向不变的维度上速度变快,梯度方向有所改变的维度上的更新速度变慢,这样就可以加快收敛并减小震荡。
从传统的SGD算法
g t = Δ θ J ( θ ) θ t + 1 = θ t − α g t g_t=\Delta_{\theta}J(\theta)\\ \theta_{t+1}=\theta_t - \alpha g_t gt=ΔθJ(θ)θt+1=θt−αgt
变成SGD-M 的形式如下
m t = β 1 m t − 1 + ( 1 − β 1 ) g t θ t + 1 = θ t − α m t m_t=\beta_1 m_{t-1} +(1-\beta_1)g_t\\ \theta_{t+1}=\theta_{t}-\alpha m_{t} mt=β1mt−1+(1−β1)gtθt+1=θt−αmt
当 β \beta β设置为 0.9 时,说明当前的动量有90%是由上一时刻的动量所贡献,只有10% 由当前的梯度决定。

加入动量的优势就是很容易跳出极小值点。
SGD-M 的一些缺点
问题:
(1)不具备一些先知,提前改变方向(没懂,可以看看后面的NAG)
(2)不能根据参数的重要性分别对待
SGD with NAG
Nesterov accelerated gradient (NAG)
在历史动量的超前点计算梯度变化,这个变化量本质上是对目标函数二阶导的近似。由于利用了二阶导的信息,NAG算法才会比Momentum具有更快的收敛速度。
从(传统)SGD算法由原来的
g t = Δ θ J ( θ ) θ t + 1 = θ t − α g t g_t=\Delta_{\theta}J(\theta)\\ \theta_{t+1}=\theta_t - \alpha g_t gt=ΔθJ(θ)θt+1=θt−αgt
变成动量NAG的形式如下
m t = β 1 m t − 1 + ( 1 − β 1 ) Δ θ J ( θ − β m t − 1 ) θ t + 1 = θ t − α m t m_t=\beta_1 m_{t-1} +(1-\beta_1)\Delta_{\theta}J(\theta-\beta m_{t-1}) \\ \theta_{t+1}=\theta_{t}-\alpha m_{t} mt=β1mt−1+(1−β1)ΔθJ(θ−βmt−1)θt+1=θt−αmt
和动量SGD相比较可以发现,历史动量那部分时相同的,不同的是:
- SGD-M:拿当前点的梯度 g t g_t gt 作为当前点的更新量,
- NAG : 拿历史动量的超前点的梯度 Δ θ J ( θ − β m t − 1 ) \Delta_{\theta}J(\theta-\beta m_{t-1}) ΔθJ(θ−βmt−1) 作为当前点更新量,相当于未卜先知
AdaGrad
想法:不同的参数 其重要性 是 不同的
对于任意一个参数,SGD, SGD-M 和 NAG 均是以相同的学习率去更新。
也就是 虽然他们计算的梯度的方式有所不同但是,但是对于他们上述更新参数的第二个式子中的 α \alpha α对于每一个参数都是一样的(第二个式子没有本质上的不同)。
AdaGrad是这样想的
➢ 对于更新不频繁的参数,希望单次步长更大,多学习一些知识;
➢ 对于更新频繁的参数,希望步长较小,使得学习到的参数更稳定,不至于被单个样本影响太多。
最终
从(传统)SGD算法由原来的
g t = Δ θ J ( θ ) θ t + 1 = θ t − α g t g_t=\Delta_{\theta}J(\theta)\\ \theta_{t+1}=\theta_t - \alpha g_t gt=ΔθJ(θ)θt+1=θt−αgt
变成动量AdaGrad的形式如下
g t = Δ θ J ( θ ) θ t + 1 = θ t − α v t m t g_t=\Delta_{\theta}J(\theta)\\ \\ \theta_{t+1}=\theta_{t}-\frac{\alpha}{v_t} m_{t} gt=ΔθJ(θ)θt+1=θt−vtαmt
α \alpha α 是全局学习率,需要手动设置, v t v_t vt是自适应学习率-自适应计算。
一般 v t = ∑ τ = 1 t g τ 2 v_t=\sum_{\tau=1}^{t}g_{\tau}^2 vt=∑τ=1tgτ2 (迄今为止所有梯度值得平方和)
缺点:
分母会不断积累,这样学习率就会收缩并最终会变得非常小,最后参数进本不会再更新
RMSprop
用窗口滑动加权平均值计算二阶动量
➢ 防止学习率的极速衰减;
➢ 不是像AdaGrad算法那样暴力直接的累加平方梯度,而是加了一个衰减系数来控制历史信息的获取多少
从(传统)SGD算法由原来的
g t = Δ θ J ( θ ) θ t + 1 = θ t − α g t g_t=\Delta_{\theta}J(\theta)\\ \theta_{t+1}=\theta_t - \alpha g_t gt=ΔθJ(θ)θt+1=θt−αgt
变成形式如下
g t = Δ θ J ( θ ) θ t + 1 = θ t − α v t m t v t = β 2 v t − 1 − ( 1 − β 2 ) g t 2 g_t=\Delta_{\theta}J(\theta)\\ \\ \theta_{t+1}=\theta_{t}-\frac{\alpha}{v_t} m_{t} \\ v_t=\beta_2v_{t-1}-(1-\beta_2)g_t^2 gt=ΔθJ(θ)θt+1=θt−vtαmtvt=β2vt−1−(1−β2)gt2
Adam = SGD-M +RMSprop
m t = β 1 m t − 1 + ( 1 − β 1 ) g t θ t + 1 = θ t − α v t m t v t = β 2 v t − 1 − ( 1 − β 2 ) g t 2 m_t=\beta_1 m_{t-1} +(1-\beta_1)g_t\\ \theta_{t+1}=\theta_{t}-\frac{\alpha}{v_t} m_{t}\\ v_t=\beta_2v_{t-1}-(1-\beta_2)g_t^2 mt=β1mt−1+(1−β1)gtθt+1=θt−vtαmtvt=β2vt−1−(1−β2)gt2
Nadam= Adam + NAG
m t = β 1 m t − 1 + ( 1 − β 1 ) Δ θ J ( θ − β m t − 1 ) θ t + 1 = θ t − α v t m t v t = β 2 v t − 1 − ( 1 − β 2 ) g t 2 m_t=\beta_1 m_{t-1} +(1-\beta_1)\Delta_{\theta}J(\theta-\beta m_{t-1}) \\ \theta_{t+1}=\theta_{t}-\frac{\alpha}{v_t} m_{t}\\ v_t=\beta_2v_{t-1}-(1-\beta_2)g_t^2 mt=β1mt−1+(1−β1)ΔθJ(θ−βmt−1)θt+1=θt−vtαmtvt=β2vt−1−(1−β2)gt2

目前实际常用的就是 一个是: SGDM (准确的来说应该是 min-Batch SGDM ,在 pytorch 中 认为还是一种SGD ,需要设置的重点参数除了 batch 大小 还有就是 动量平滑因子 一般设置成0.9 ,0设置成零就是不用历史动量,学习率等), 另一个就是 Adam (一般设置 全局学习率等)
思考:知乎问题: Adam那么棒,为什么还对SGD念念不忘?
这篇文章大概是在说: SGD 好像是 智能手机出现之前的相机,而Adam就像是能够自动调焦的傻瓜相机。
Adam可能有以下缺点:
- 1、可能不收敛 [文献 On the Convergence of Adam and Beyond ]
传统的手段一般是由收敛依据的。如 SGD没有用到二阶动量,因此学习率是恒定的(实际使用过程中会采用学习率衰减策略,因此学习率递减)。AdaGrad的二阶动量不断累积,单调递增,因此学习率是单调递减的。因此,这两类算法会使得学习率不断递减,最终收敛到0,模型也得以收敛。但AdaDelta和Adam则不然。他用的二阶动量是固定时间窗口内的累积,随着时间窗口的变化,遇到的数据可能发生巨变,使得 可能会时大时小,不是单调变化。这就可能在训练后期引起学习率的震荡,导致模型无法收敛。
文献给出了解决方案:对二阶动量的变化进行控制,避免上下波动。
V t = m a x ( β 2 ∗ V t − 1 + ( 1 − β 2 ) g t 2 , V t − 1 ) V_t=max(\beta_2 *V_{t-1}+(1-\beta_2)g_t^2,V_{t-1}) Vt=max(β2∗Vt−1+(1−β2)gt2,Vt−1)
这样保证了这一时刻的二阶动量一定小于上一时刻的二阶动量,从而学习率递减 - 可能错过全局最优解
很多人认为即使引入动量的概念也极有可能错过全局最优解
[文献一 The Marginal Value of Adaptive Gradient Methods in Machine Learning ] 中说同样的一个优化问题,不同的优化算法可能会找到不同的答案,但自适应学习率的算法往往找到非常差的答案。他们通过一个特定的数据例子说明,自适应学习率算法可能会对前期出现的特征过拟合,后期才出现的特征很难纠正前期的拟合效果。
[文献2 Improving Generalization Performance by Switching from Adam to SGD ] 进行了实验验证。他们CIFAR-10数据集上进行测试,Adam的收敛速度比SGD要快,但最终收敛的结果并没有SGD好。他们进一步实验发现,主要是后期Adam的学习率太低,影响了有效的收敛。他们试着对Adam的学习率的下界进行控制,发现效果好了很多。
于是他们提出了一个用来改进Adam的方法:前期用Adam,享受Adam快速收敛的优势;后期切换到SGD,慢慢寻找最优解。这一方法以前也被研究者们用到,不过主要是根据经验来选择切换的时机和切换后的学习率。这篇文章把这一切换过程傻瓜化,给出了切换SGD的时机选择方法,以及学习率的计算方法,效果看起来也不错。
知乎系列文章的第三篇讲解了 1、什么时候切换优化算法?2、切换算法以后用什么样的学习率?这两个问题 - 最后作者 进行了总结 认为,没有纠结Adam还是SGD好的必要,认为算法固然美好,数据才是根本。
梯度折断
一种比较简单的启发式方法,把梯度的模限定在一个区间,当梯度的模小于或大于这个区间时就进行截断 (没懂)
在反向传播的过程中会产生梯度消失/梯度爆炸的问题,梯度消失/爆炸会导致网络中的参数长时间无法更新,模型进而无法得到很好的训练效果。梯度截断,就是要解决 梯度消失/梯度爆炸 的问题,也就是设定阈值,当预更新的梯度小于阈值时,那么将预更新的梯度设置为阈值,梯度截断通常发送在,损失函数反向传播计算完之后,优化器梯度更新之前。
g t = m a x ( m i n ( g t , b ) , a ) g_t=max(min(g_t,b),a) gt=max(min(gt,b),a)
小结
参数初始化
梯度下降法需要在开始训练时给每一个参数赋一个初始值。
➢ 初始化为0:对称权重问题 :所有参数为0 --> 神经元输出相同 → BP梯度相同 → 参数更新相同 → 参数相同
➢ 初始化太小:导致神经元的输入过小,随着层数的不断增加,会出现信号消失的问题;也会导致sigmoid激活函数丢失非线性的能力,因为在 0 附近sigmoid函数近似是线性的。
➢ 初始化太大:导致输入状态太大,对sigmoid激活函数来说,激活函数的值会变得饱和,从而出现梯度消失的问题。
初始化方法
➢ 预训练初始化 就是先用一个模型训练,将训练后的参数作为初始化的参数结果
➢ 随机初始化(基于方差缩放):xavier与kaiming
➢ 固定值初始化:偏置一般固定为0
方差缩放
保证每层网络输出的数值范围都稳定在一个区间中
要高效地训练神经网络,给参数选取一个合适的随机初始化区间是非常重要的。一般而言,参数初
始化的区间应该根据神经元的性质进行差异化的设置。
如果一个神经元的输入连接很多,它的每个输入连接上的权重就应该小一些,以避免神经元的输出
过大(当激活函数为 ReLU 时)或过饱和(当激活函数为Sigmoid函数时)。
定义:初始化一个深度网络时,为了缓解梯度消失或爆炸问题,我们尽可能保持每个神经元的输入和
输出的方差一致,根据神经元的连接数量来自适应地调整初始化分布的方差,这类方法称为
方差缩放 (Variance Scaling)。
Xavier参数初始化(tanh 、 sigmoid )
某全连接层的计算方式如下: z = w 1 x 1 + ⋯ + w n i n x n in ( n in z=w_1 \mathrm{x}_1+\cdots+w_{n_{i n}} x_{n_{\text {in }}}\left(n_{\text {in }}\right. z=w1x1+⋯+wninxnin (nin 为输入节点数 ) ) ),
激活函数为线性函数, 且在 0 附近导数为 1 , 例如 t a n h t a n h tanh 。
y = tanh ( z ) ≈ w 1 x 1 + ⋯ + w n in x n in , y=\tanh (z) \approx w_1 \mathrm{x}_1+\cdots+w_{n_{\text {in }}} x_{n_{\text {in }}}, y=tanh(z)≈w1x1+⋯+wnin xnin ,
输出方差计算如下:
var ( y ) = var ( w 1 x 1 + ⋯ + w n i n x n i n ) = n i n var ( w i x i ) = n in ( E [ w i ] 2 var ( x i ) + E [ x i ] 2 var ( w i ) + var ( w i ) var ( x i ) ) = n i n var ( w i ) var ( x i ) , \begin{aligned} &\operatorname{var}(y)=\operatorname{var}\left(w_1 \mathrm{x}_1+\cdots+w_{n_{i n}} x_{n_{i n}}\right)=n_{i n} \operatorname{var}\left(w_i x_i\right) \\ &=n_{\text {in }}\left(E\left[w_i\right]^2 \operatorname{var}\left(x_i\right)+E\left[x_i\right]^2 \operatorname{var}\left(w_i\right)+\operatorname{var}\left(w_i\right) \operatorname{var}\left(x_i\right)\right)=n_{i n} \operatorname{var}\left(w_i\right) \operatorname{var}\left(x_i\right), \end{aligned} var(y)=var(w1x1+⋯+wninxnin)=ninvar(wixi)=nin (E[wi]2var(xi)+E[xi]2var(wi)+var(wi)var(xi))=ninvar(wi)var(xi),
为了保证输入输出方差一致 var ( y ) = var ( x ) \operatorname{var}(y)=\operatorname{var}(x) var(y)=var(x), 则 var ( w i ) = 1 n i n \operatorname{var}\left(w_i\right)=\frac{1}{n_{i n}} var(wi)=nin1,
同理,反向传播中,为了使误差信号也不被放大缩小, 则 var ( w i ) = 1 n out ( n out \operatorname{var}\left(w_i\right)=\frac{1}{n_{\text {out }}}\left(n_{\text {out }}\right. var(wi)=nout 1(nout 为输出节点数),
综合前向和反向传播进行折中,权重参数的方差应该为
var ( w i ) = 2 n in + n out \operatorname{var}\left(w_i\right)=\frac{2}{n_{\text {in }}+n_{\text {out }}}{ } var(wi)=nin +nout 2
利用计算得到的方差 var ( w i ) = 2 n in + n out \operatorname{var}\left(w_i\right)=\frac{2}{n_{\text {in }}+n_{\text {out }}}{ } var(wi)=nin +nout 2, 可采用高斯分布或者均匀分布来随机初始化参数:
- 高斯分布 N ( 0 , 2 n in + n out ) N(0,\frac{2}{n_{\text {in }}+n_{\text {out }}} ) N(0,nin +nout 2)
- 均匀分布 U [ − 6 n in + n out , 6 n in + n out ] U[-\sqrt{\frac{6}{n_{\text {in }}+n_{\text {out }}}},\sqrt{\frac{6}{n_{\text {in }}+n_{\text {out }}}}] U[−nin +nout 6,nin +nout 6] ( 均匀分布方差为: ( a − b ) 2 / 12 (a-b)^2/12 (a−b)2/12 倒推范围)
- logistic激活函数 N ( 0 , 16 ∗ 2 n in + n out ) N(0,16*\frac{2}{n_{\text {in }}+n_{\text {out }}}) N(0,16∗nin +nout 2) (因为之前假设激活函数是 tanh 0附近导数约为 1,如果是 sigmoid 0 附近导数约为 1/4 ,也即 y =(1/4) *z ,带入上式求方差的过程即可得到结论)
Kamming初始化 (ReLU )
使用ReLU激活函数时,只有一半的神经元输出为0,因此其分布的方差也近似为使用恒等函数时的
一半。
也即上一小节推导 方差的过程中时, var ( w i ) = 1 n i n \operatorname{var}\left(w_i\right)=\frac{1}{n_{i n}} var(wi)=nin1,改成 var ( w i ) = 2 n i n \operatorname{var}\left(w_i\right)=\frac{2}{n_{i n}} var(wi)=nin2 [ 推导 ]

数据预处理
数据输入归一化
预处理大部分都在说数据的归一化问题,常见的归一化方案有:
- 最小最大值归一化
- 标准化(最常用)
- PCA
标准化即求数据的(各个维度)均值和方差,然后对 减去均值 除以 方差 (即 变成“标准正态分布的过程”,实际如果要进行标准,还考虑各维度之间的相关性)
μ = 1 N ∑ n = 1 N x ( n ) σ 2 = 1 N ∑ n = 1 N ( x ( n ) − μ ) 2 \mu=\frac{1}{N}\sum_{n=1}^{N}x^{(n)}\\ \sigma^2=\frac{1}{N}\sum_{n=1}^N{(x^{(n)}-\mu )^2} μ=N1∑n=1Nx(n)σ2=N1∑n=1N(x(n)−μ)2
实际建议:
以RGB彩色图像为例
➢ 简单缩放 [0,255](int8) → [0,1](float)
➢ 标准化:减均值+除标准差
μ = 1 N ∑ n = 1 N x ( n ) σ 2 = 1 N ∑ n = 1 N ( x ( n ) − μ ) 2 \mu=\frac{1}{N}\sum_{n=1}^{N}x^{(n)}\\ \sigma^2=\frac{1}{N}\sum_{n=1}^N{(x^{(n)}-\mu )^2} μ=N1∑n=1Nx(n)σ2=N1∑n=1N(x(n)−μ)2
Q:输入数据归一化了,中间输出数据如何?
A:逐层归一化,具体怎么操作见下一小节(这里仅讨论 输入数据的预处理)
归一化
目的
➢ 更好的尺度不变性
➢ 更平滑的优化地形
网络中间层归一化的常用方法
➢ 批量归一化(Batch Normalization,BN)(常用)
➢ 层归一化(Layer Normalization,LN)(常用)
➢ 实例归一化(Instance Normalization,IN)
➢ 组归一化(Group Normalization,GN)
BN(Batch Normalization)
BN 主要用于解决 Covariate Shift(方差偏移)的问题
Covariate Shift
- 训练的数据和测试的数据本身分布就不一样,那么训练后的模型就很难泛化到测试集上。
- 在输入数据经过网络内部计算后,分布发生了变化,这样导致数据变得不稳定,从而导致网络寻找最优解的过程变得缓慢,训练速度会下降。
BN的解决方案:对每一层的输出进行归一化 (减均值、除方差(标准差))
Input : × ,其中是一个batch 样本的的个数,为channel维度 ,也即每一个样本对应的多少维度
μ j = 1 N ∑ i = 1 N x i , j ( 1 × D ) σ 2 = 1 N ∑ n = 1 N ( x i , j − μ j ) 2 ( 1 × D ) x ^ i , j = x i , j − μ j σ j 2 + ε ( N × D ) \mu_j=\frac{1}{N}\sum_{i=1}^{N}x_{i,j}\quad(1\times D)\\ \sigma^2=\frac{1}{N}\sum_{n=1}^N{(x_{i,j}-\mu_j )^2}\quad(1\times D)\\ \hat{x}_{i,j}=\frac{x_{i,j}-\mu_j}{\sqrt{\sigma^2_j+\varepsilon}}\quad(N\times D) μj=N1i=1∑Nxi,j(1×D)σ2=N1n=1∑N(xi,j−μj)2(1×D)x^i,j=σj2+εxi,j−μj(N×D)
问题:输出变为0均值1方差,会降低网络的表达能力
因为sigmoid 等激活函数在z=0时,函数输出结果会近似于一个线性函数的输出结果,会降低网络的非线性表达能力
为了解决上述问题,BN算法在以上过程的基础上,在结果上增加了加入可学习的偏移和缩放系数, γ j \gamma_j γj, β j \beta_j βj
,(相当于又加了一个权重和偏置的操作):总体下来,BN归一化的操作变成了:
μ j = 1 N ∑ i = 1 N x i , j ( 1 × D ) σ 2 = 1 N ∑ n = 1 N ( x i , j − μ j ) 2 ( 1 × D ) x ^ i , j = x i , j − μ j σ j 2 + ε ( N × D ) y i , j = γ j x ^ i , j + β j ( N × D ) \mu_j=\frac{1}{N}\sum_{i=1}^{N}x_{i,j}\quad(1\times D)\\ \sigma^2=\frac{1}{N}\sum_{n=1}^N{(x_{i,j}-\mu_j )^2}\quad(1\times D)\\ \hat{x}_{i,j}=\frac{x_{i,j}-\mu_j}{\sqrt{\sigma^2_j+\varepsilon}}\quad(N\times D)\\ y_{i,j}=\gamma_j \hat{x}_{i,j} +\beta_j (N\times D) μj=N1i=1∑Nxi,j(1×D)σ2=N1n=1∑N(xi,j−μj)2(1×D)x^i,j=σj2+εxi,j−μj(N×D)yi,j=γjx^i,j+βj(N×D)
均值和方差是通过batch数据学习的,测试阶段怎么办?
A:保留部分训练得到的均值和方差,和测试集中的均值和方差进行加权求和即
μ = β μ + ( 1 − β ) μ σ 2 = β σ 2 + ( 1 − β ) σ j 2 \mu=\beta\mu+(1-\beta)\mu\\ \sigma^2=\beta \sigma^2+(1-\beta)\sigma_j^2 μ=βμ+(1−β)μσ2=βσ2+(1−β)σj2
对于全连接层来说
Batch Normalization for Fully Connected Layer
输入: X : N × D X:N\times D X:N×D
归一化后:
均值,方差: μ , σ : 1 × D \mu,\sigma:1\times D μ,σ:1×D
偏移和缩放系数: γ , β : 1 × D \gamma,\beta:1\times D γ,β:1×D
归一化结果: y = γ ( x − μ ) σ + β y=\frac{\gamma(x-\mu)}{\sigma}+\beta y=σγ(x−μ)+β
对于卷积层来说
Batch Normalization for Convolutional Layer
(Spatial Batchnorm,BatchNorm 2D)
输入: X : N × C × H × W X:N\times C\times H\times W X:N×C×H×W (C这里为通道数)
归一化后:
均值,方差: μ , σ : 1 × C × 1 × 1 \mu,\sigma:1\times C \times 1 \times 1 μ,σ:1×C×1×1
偏移和缩放系数: γ , β : μ , σ : 1 × C × 1 × 1 \gamma,\beta:\mu,\sigma:1\times C \times 1 \times 1 γ,β:μ,σ:1×C×1×1
归一化结果: y = γ ( x − μ ) σ + β y=\frac{\gamma(x-\mu)}{\sigma}+\beta y=σγ(x−μ)+β
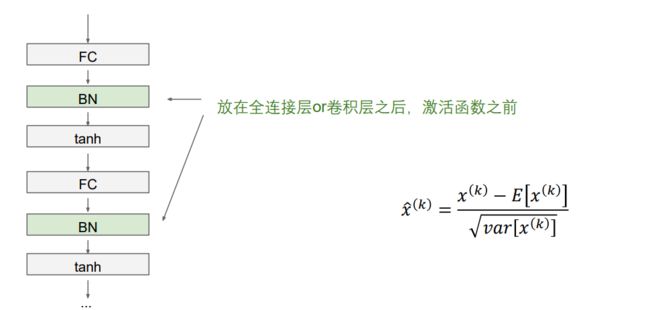
BN层的位置一般放在 全连接层or卷积层之后,激活函数之前
问题: batchsize很小,比如bs=1,BN无法使用。
如果bs比较小,均值方差波动范围比较大,这样章计算的均值和方差没什么意义。
解决方案? Layer Normalization
LN(Layer Normalization)
相比于BN,LN求取均值和方差的过程是,不管样本个数,只从单个样本入手,求的是单个样本的均值和方差。
那么他的归一化过程大致可以写成
μ i = 1 D ∑ j = 1 D x i , j ( 1 × N ) σ i 2 = 1 D ∑ j = 1 D ( x i , j − μ i ) 2 ( 1 × N ) x ^ i , j = x i , j − μ i σ i 2 + ε ( N × D ) y i , j = γ j x ^ i , j + β j ( N × D ) \mu_i=\frac{1}{D}\sum_{j=1}^{D}x_{i,j}\quad(1\times N)\\ \sigma_i^2=\frac{1}{D}\sum_{j=1}^D{(x_{i,j}-\mu_i)^2}\quad(1\times N)\\ \hat{x}_{i,j}=\frac{x_{i,j}-\mu_i}{\sqrt{\sigma^2_i+\varepsilon}}\quad(N\times D)\\ y_{i,j}=\gamma_j \hat{x}_{i,j} +\beta_j (N\times D) μi=D1j=1∑Dxi,j(1×N)σi2=D1j=1∑D(xi,j−μi)2(1×N)x^i,j=σi2+εxi,j−μi(N×D)yi,j=γjx^i,j+βj(N×D)
对于全连接层来说
Layer Normalization for Fully Connected Layer
输入: X : N × D X:N\times D X:N×D
归一化后:
均值,方差: μ , σ : N × 1 \mu,\sigma:N\times 1 μ,σ:N×1
偏移和缩放系数: γ , β : 1 × D \gamma,\beta:1\times D γ,β:1×D
归一化结果: y = γ ( x − μ ) σ + β y=\frac{\gamma(x-\mu)}{\sigma}+\beta y=σγ(x−μ)+β
对于卷积层来说
Layer Normalization for Convolutional Layer
(Spatial Batchnorm,BatchNorm 2D)
输入: X : N × C × H × W X:N\times C\times H\times W X:N×C×H×W (C这里为通道数)
归一化后:
均值,方差: μ , σ : N × 1 × 1 × 1 \mu,\sigma:N\times 1 \times 1 \times 1 μ,σ:N×1×1×1
偏移和缩放系数: γ , β : μ , σ : 1 × C × 1 × 1 \gamma,\beta:\mu,\sigma:1\times C \times 1 \times 1 γ,β:μ,σ:1×C×1×1
归一化结果: y = γ ( x − μ ) σ + β y=\frac{\gamma(x-\mu)}{\sigma}+\beta y=σγ(x−μ)+β
归一化方法总结
正则化(防止过拟合)
目的:通过加入正则项,防止过拟合,提高神经网络泛化能力
常用的网络防止过拟合方案
➢ 1, 2 正则化
➢ early stop(提前停止)
➢ Dropout
➢ data augmentation(数据增强)
L1、L2 正则化
通过约束参数的1和2范数,降低参数数值,防止过拟合风险
这里的参数指的是正则化部分的数值数值大小,参数值越小代表模型越简单:越复杂的模型,越是会尝试对所有的样本进行拟合,容易造成在较小的区间里预测值产生较大的波动,这种较大的波动也反映了在这个区间里的导数很大,而只有较大的参数值才可以产生较大的导数。
优化目标:
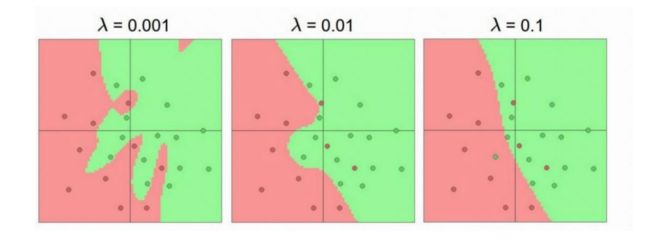
L ′ ( θ ) = L ( θ ) + λ l p ( θ ) L'(\boldsymbol{\theta})=L(\boldsymbol{\theta})+\lambda \mathit{l}_p(\boldsymbol{\theta}) L′(θ)=L(θ)+λlp(θ)
等号右边第一项 L ( θ ) L(\boldsymbol{\theta}) L(θ) 代表原始损失,第二项 中的 l p ( θ ) \mathit{l}_p(\boldsymbol{\theta}) lp(θ)代表范数损失, l p ( ⋅ ) \mathit{l}_p( \sdot ) lp(⋅) 代表范数函数,的取值通常为 1,2 ,分别代表1和2范数 λ \lambda λ 一般是一个超参数,需要手动设置
PS: L 0 L_0 L0范数是指一个向量中非零元素的个数,他没有办法求导,所以一般不用
L 1 L_1 L1正则、 L 2 L_2 L2正则
➢ 1 正则:权重中各个元素的绝对值之和,用于产生稀疏矩阵;
➢ 2 正则:权重中各个元素的平方和,用于降低参数的数值。
- L 1 L_1 L1由于导数是一个sign 函数,只要元素不等于零,梯度就一直为 ±1,这导致经过L1正则化后,很多参数会为零 (物理意义上,有参数选择的作用)
- L 2 L_2 L2由于导数是一个过零点的一次函数,接近于零时,导数值越接近零,这导致经过L2正则化之后,很多参数会很小,但是不等于零 (由于求导方便L2正则用的还是比较多)
ℓ 2 \ell_2 ℓ2 正则化: L ′ ( θ ) = L ( θ ) + λ 1 2 ∥ θ ∥ 2 ∂ L ′ ∂ θ = ∂ L ∂ θ + λ θ \quad \mathrm{L}^{\prime}(\theta)=L(\theta)+\lambda \frac{1}{2}\|\theta\|_2 \frac{\partial \mathrm{L}^{\prime}}{\partial \theta}=\frac{\partial \mathrm{L}}{\partial \theta}+\lambda \theta L′(θ)=L(θ)+λ21∥θ∥2∂θ∂L′=∂θ∂L+λθ
θ t + 1 → θ t − α ∂ L ′ ∂ θ = θ t − α ( ∂ L ∂ θ + λ θ t ) = ( 1 − α λ ) θ t − α ∂ L ∂ θ \theta^{t+1} \rightarrow \theta^t-\alpha \frac{\partial \mathrm{L}^{\prime}}{\partial \theta}=\theta^t-\alpha\left(\frac{\partial \mathrm{L}}{\partial \theta}+\lambda \theta^t\right)=(1-\alpha \lambda) \theta^t-\alpha \frac{\partial \mathrm{L}}{\partial \theta} θt+1→θt−α∂θ∂L′=θt−α(∂θ∂L+λθt)=(1−αλ)θt−α∂θ∂L
ℓ 1 \ell_1 ℓ1 正则化: L ′ ( θ ) = L ( θ ) + λ 1 2 ∥ θ ∥ 1 ∂ L ′ ∂ θ = ∂ L ∂ θ + λ sgn ( θ ) \quad \mathrm{L}^{\prime}(\theta)=L(\theta)+\lambda \frac{1}{2}\|\theta\|_1 \quad \frac{\partial \mathrm{L}^{\prime}}{\partial \theta}=\frac{\partial \mathrm{L}}{\partial \theta}+\lambda \operatorname{sgn}(\theta) L′(θ)=L(θ)+λ21∥θ∥1∂θ∂L′=∂θ∂L+λsgn(θ)
θ t + 1 → θ t − α ∂ L ′ ∂ θ = θ t − α ( ∂ L ∂ θ + λ sgn ( θ t ) ) = θ t − α ∂ L ∂ θ − α λ sgn ( θ t ) \theta^{t+1} \rightarrow \theta^t-\alpha \frac{\partial \mathrm{L}^{\prime}}{\partial \theta}=\theta^t-\alpha\left(\frac{\partial \mathrm{L}}{\partial \theta}+\lambda \operatorname{sgn}\left(\theta^t\right)\right)=\theta^t-\alpha \frac{\partial \mathrm{L}}{\partial \theta}-\alpha \lambda \operatorname{sgn}\left(\theta^t\right) θt+1→θt−α∂θ∂L′=θt−α(∂θ∂L+λsgn(θt))=θt−α∂θ∂L−αλsgn(θt)
early stop
使用一个验证集来测试每一次迭代的参数在验证集上是否最优,
如果在验证集上的错误率不再下降,损失有扩大的风险,就停止迭代。
dropout
- 训练时将某些结果的输出以一定概率被丢弃(置为0),
- 测试时所有节点输出值乘概率
为什么有用?
➢ 组合派:每次训练一个“瘦小”的网络,测试阶段组合这几个模型的输出,提高泛化能力;(类似于训练了好几个模型,输出的结果是好几个模型的平均值)
➢ 生物进化: 强迫一个神经单元,和随机挑选出来的其他神经单元共同工作,达到好的效果。消除减弱了神经元节点间的联合适应性,增强了泛化能力。
Data Augmentation
数据增强
CV方面用的多:
通过算法对图像进行转变,引入噪声等方法来增加数据的多样性以及训练数据量
➢ 旋转(Rotation):将图像按顺时针或逆时针方向随机旋转一定角度;
➢ 翻转(Flip):将图像沿水平或垂直方法随机翻转一定角度;
➢ 缩放(Zoom In/Out):将图像放大或缩小一定比例;
➢ 平移(Shift):将图像沿水平或垂直方向平移一定步长;
➢ 加噪声(Noise):加入随机噪声。