Darknet卷积层算力评估
darknet是用C语言开发的一款非常精简高效的推理框架，它的开发者也是YOLO的作者，关于darknet推理环境的介绍网上有很多，不再过多介绍，这里只是尝试解读darknet推理过程中的一些细节知识点，就从推理输出的算力来源开始。
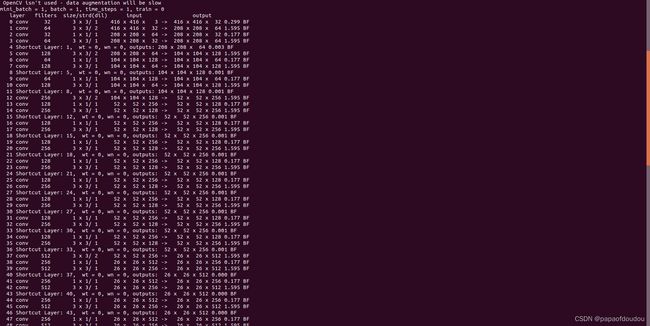
一张经典的输出：
推理过程中的LOG显示中，BF是BFOPS的缩写，它表示什么意思呢？BFLOPS 有两个不同场景下的解释。 第一种是描述硬件运算性能的单位，这时其全称是Billion Float Operations Per Second，即每秒能进行多少个十亿次浮点运算； 第二种是描述某次卷积运算需要的多少个十亿次浮点运算，其全称是Billion FLoat OPerationS，将多次卷积等运算所耗费的BLOPS加起来就可以来表示 某个算法模型的复杂度。
在标准的单位中，BFOPS叫做GFOPS，表示每秒10亿次的浮点计算。它和TFOPS有个简单的换算关系，那就是：1TFOPS=1000GFOPS=1000BFOPS.
现在我们看一下推理输出的BFOPS是如何计算出来的，以第一层输入层为例：
可以看到这一层需要的总共算例为：0.299 BF，怎么计算得来的呢？
下面这篇博客有详细的理论分析：
卷积层的算力评估(MACC和FOPS)_papaofdoudou的博客-CSDN博客
这里我们只把结论搬过来：
也就是说，完成卷积需要的总的浮点计算次数为：卷集核长*卷集核宽*2*输出图长*输出图宽*卷集核个数*每个卷集核的通道数。
其中，卷集核长*卷集核宽*每个卷集核的通道数*卷集核个数也表示本层需要的权重参数的个数。
所以以上公式可以简化为：卷集层总算力=本层需要的权重参数的个数*输出图长*输出图宽*2。
而且，卷集核长*卷集核宽*每个卷集核的通道数，多么像一个卷集核的“体积”？
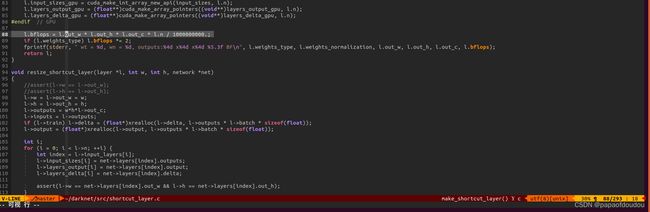
对应于darknet中的l.bflops的实现，l代表当前层，是面向对象的写法。
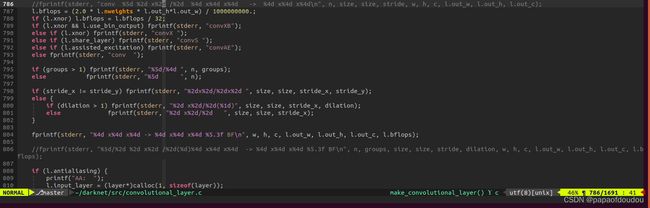接下来，我们就验证一下上面的输出结果，对于第一层来说，如下图：
根据以上公式，总的算力计算为：
3*3*2*416*416*32*3=299040768≈0.299 billion float operations = 0.299BF
理论计算和实际结果符合，证明我们的计算方法是正确的。
总算力是多少？
darknet推理结束后，得到的总算力值是65.879 bflops,按照前面介绍的关系进行单位换算，也就是0.065879TFOPS,所以如果以在1T算力的NPU上跑，帧率应为 1/0.065879 = 15.1793439488 FPS. 和VIP的仿真输出差不多。
VIP仿真数据13帧多一点：
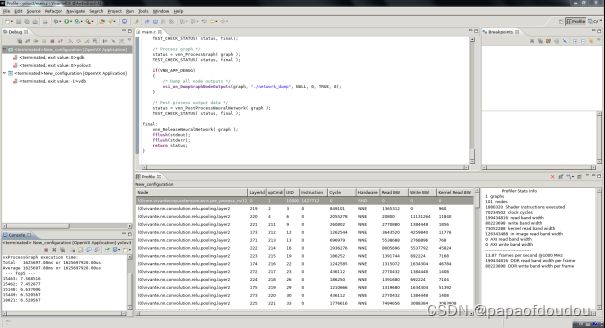
pegasus算力评估输出
可以看到,pegasus measure --model yolov3.cfg输出的算力评估结果如下，大头在 macc，单位达到了GFOPS， GFOPS=BFOPS，都是十亿的单位。
pegasus计算出来的yolov3网络算力是32.99G mac 数，转换成浮点，需要再乘以2，所以总的算力是32.99*2=65.98GFOPS.和上面darknet得出的65.879GOPS的误差几乎可以忽略不计。
再次证明，网络的结构决定了算力的大小，和其它的因素无关。
用同样的方式，分析第二层：
总算力=208*208*64*3*3*32*2=1594884096 FOPS = 1594884096/1000000000 BFOPS(GFOPS) = 1.59488 BFOPS算力，理论计算和实际输出符合。
另外，根据
darknet pad默认为1，这一层的步长为2，所以，输出尺寸计算公式为：
之所以出现小数，可能是因为实际的填充情况是左边和右边只填充了一边把,dialation 和 stride是同一个意思，都是步长吧,默认为1。
shortcut层算力评估：
以第四层为例：
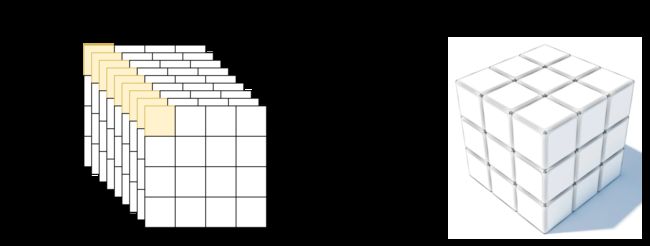
在网络结构图中，它的结构如下，两个shape为208*208*64的tensor合并为一个208*208*64的tensor.
在darknet实现中，它的算力计算公式为：
所以以为上面的shortcut为例，它的总算力需求为：
208*208*64=2768896FOPS = 2768896/1000000 BFLOPS(GFLOPS) = 0.002768896≈0.3BF.
算法逻辑如下，两个TENSOR对应维度相同的成员相加，TENSOR 形状保持不变。
影响算力的因素
根据前面计算算力的公式：
卷集核长*卷集核宽*2*输出图长*输出图宽*卷集核个数*每个卷集核的通道数。
我们可以知道，卷积层的算力和输出图长和宽都成正比关系，又根据：
输出feature map尺寸和输入图的尺寸也成线性关系，所以追究下来，卷积层的总算里和输入图的尺寸成正相关，输入图尺寸越大，所需总算力越大。
darknet支持三种格式的图像输入尺寸供我们验证，分别是320x320,416x416和608x608，我们分别验证，将尺寸修改为上面另外的两种，各层算力需求发生什么变化：
首先是608x608，修改很简单，直接修改yolov3.cfg文件net层的参数即可：
推理输出：
可以看到，输入图尺寸变大后，各层算力出现了明显增大，以前两层为例，前后变化比例为：
0.639/0.299=2.1371237458193979933110367892977
3.407/1.595=2.1360501567398119122257053291536
误差很小近似成正比关系，我们在对比以下输入从416x416变到608x608，图像的尺寸变化比例：
所以，算力和图形的面积尺寸成正比，图形越大，算力越大，和图形的二维面积成正比。
推理效果，貌似图像尺寸变大后，推理效果更好了：
如果换成320x320，算力变化也是一样的：
1.595/0.944=1.6896186440677966101694915254237
也是完美符合尺寸正比的规律。来看一下320x320推理的效果：
总结：
320x320,416x416,608x608,推理效果上随着推理输入图尺寸增加也增加，看来高算力不白给，精度也高啊。