支持向量机

事实上在线性分析中遇到的许多分类问题并不是线性可分的，而是线性不可分的，使两个超平面的距离相等称为最优超平面 距离最优超平面。

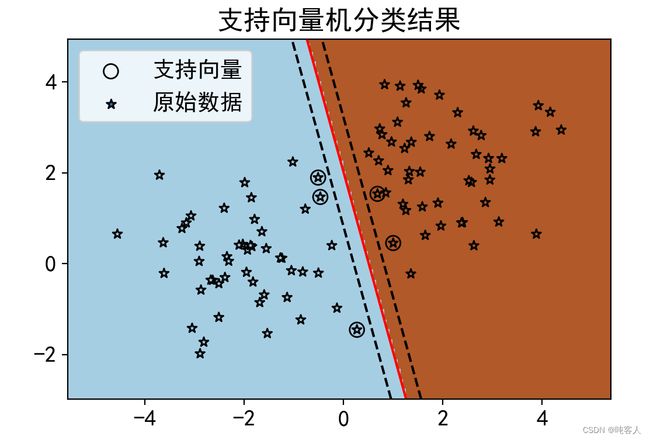
使用SVC() 训练二元类别数据集的支持向量机分类

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn import svm
#使用样本生成器生成数据集\n",
#使用make_blobs生成centers个类的数据集X，X形状为(n_samples,n_features)\n",
#指定每个类的中心位置，y返回类标签\n",

from sklearn.datasets import make_blobs
centers = [(-2, 0), (2, 2)]
X, y = make_blobs(n_samples=100, centers=centers, n_features=2,
                   random_state=0)
# 使用支持向量机进行训练\n",
#可选择不同的核函数kernel： 'linear', 'poly', 'rbf','sigmoid'\n",
clf = svm.SVC(kernel='linear',gamma=2)
clf.fit(X, y)
#观察训练的支持向量机模型各个属性\n",
print('支持向量在训练集中的索引为：',clf.support_)
print('支持向量为：\\n',clf.support_vectors_ )
print('每个类的支持向量的数量为：',clf.n_support_)

plt.figure(figsize=(6, 4))
plt.rc('font', size=14)#设置图中字号大小\n",
plt.rcParams['font.sans-serif'] = 'SimHei'#设置字体为SimHei显示中文\n",
plt.rcParams['axes.unicode_minus']=False#坐标轴刻度显示负号\n",
#获得支持向量，绘制其散点图，默认以圆圈表示\n",
plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], s=80,
                facecolors='none', zorder=10, edgecolors='k')
#绘制原始数据散点图，以*表示\n",
plt.scatter(X[:, 0], X[:, 1], c=y,marker='*', zorder=10, cmap=plt.cm.Paired,
                edgecolors='k')
plt.legend(['支持向量','原始数据'])
x_min,x_max=np.min(X[:,0])-1,np.max(X[:,0])+1
y_min,y_max=np.min(X[:,1])-1,np.max(X[:,1])+1
#绘制等高线\n",
#XX, YY分别从最小值到最大值间均匀取200个数，形状都为200*200\n",
XX, YY = np.mgrid[x_min:x_max:200j, y_min:y_max:200j]
#XX.ravel(), YY.ravel()分别将XX, YY展平为40000*1的数组\n",
#np.c_[XX.ravel(), YY.ravel()]的形状为40000*2\n",
#计算XX, YY规定的平面内每个点到分割超平面的函数距离\n",
Z = clf.decision_function(np.c_[XX.ravel(), YY.ravel()])
#设置Z的形状与XX相同，准备将Z的值与XX,YY规定的平面内的每一点的颜色值关联\n",
Z = Z.reshape(XX.shape)
#Z>0返回True或False\n",
#以点到超平面的距离0为分界线（即超平面自身），用两种颜色(1和0)绘制超平面的两侧\n",
plt.pcolormesh(XX, YY, Z>0, cmap=plt.cm.Paired)
#绘制等高线，连接XX,YY规定的平面上具有相同Z值的点,等高线的值由levels规定\n",
plt.contour(XX, YY, Z, colors=['k', 'r', 'k'], linestyles=['--', '-', '--'],
                levels=[-.5, 0, .5])
#对XX,YY规定的平面设置坐标轴刻度范围\n",
plt.xlim(x_min, x_max)
plt.ylim(y_min, y_max)
plt.title('支持向量机分类结果')#添加标题\n"
plt.show()

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn import svm
#使用样本生成器生成数据集\n",
#使用make_blobs生成centers个类的数据集X，X形状为(n_samples,n_features)\n",
#指定每个类的中心位置，y返回类标签\n",
from sklearn.datasets import make_blobs
centers = [(-2, 0), (2, 2)]
X, y = make_blobs(n_samples=100, centers=centers, n_features=2,
                   random_state=0)
#可视化原始样本、支持向量、分类超平面和等高线\n",
x_min,x_max=np.min(X[:,0])-1,np.max(X[:,0])+1
y_min,y_max=np.min(X[:,1])-1,np.max(X[:,1])+1
plt.rc('font', size=14)#设置图中字号大小\n",
plt.rcParams['font.sans-serif'] = 'SimHei'#设置字体为SimHei显示中文\n",
plt.rcParams['axes.unicode_minus']=False#坐标轴刻度显示负号\n",
p=plt.figure(figsize=(12, 8))
kernels=['linear', 'poly', 'rbf','sigmoid']
figNum=[1,2,3,4]
for kernel,i in zip(kernels,figNum):#zip()用于非嵌套的多个变量的循环\n",
# 使用支持向量机进行训练\n",
    clf = svm.SVC(kernel=kernel,gamma=2)
    clf.fit(X, y)
  #可视化\n",\
    #获得支持向量，绘制其散点图，默认以圆圈表示\n",
    ax1 = p.add_subplot(2,2,i)
    plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], s=80,
               facecolors='none', zorder=10, edgecolors='k')
    #绘制原始数据散点图，以*表示ddd
    plt.scatter(X[:, 0], X[:, 1], c=y,marker='*', zorder=10, cmap=plt.cm.Paired,
                edgecolors='k')
    #XX, YY分别从最小值到最大值间均匀取200个数，形状都为200*200\n",
    XX, YY = np.mgrid[x_min:x_max:200j, y_min:y_max:200j]
    #XX.ravel(), YY.ravel()分别将XX, YY展平为40000*1的数组\n",
    #np.c_[XX.ravel(), YY.ravel()]的形状为40000*2\n",
    #计算XX, YY规定的平面内每个点到分割超平面的函数距离\n",
    Z = clf.decision_function(np.c_[XX.ravel(), YY.ravel()])
    #设置Z的形状与XX相同，准备将Z的值与XX,YY规定的平面内的每一点的颜色值关联\n",
    Z = Z.reshape(XX.shape)
    #Z>0返回True或False\n",
    #以点到超平面的距离0为分界线（即超平面自身），\n",
    #用两种颜色(1和0)绘制超平面的两侧\n",
    plt.pcolormesh(XX, YY, Z>0, cmap=plt.cm.Paired)
    #绘制等高线，连接XX,YY规定的平面上具有相同Z值的点,等高线的值由levels规定\n",
    plt.contour(XX, YY, Z, colors=['k', 'r', 'k'], linestyles=['--', '-', '--'],
                levels=[-.5, 0, .5])
    #对XX,YY规定的平面设置坐标轴刻度范围\n",
    plt.xlim(x_min, x_max)
    plt.ylim(y_min, y_max)
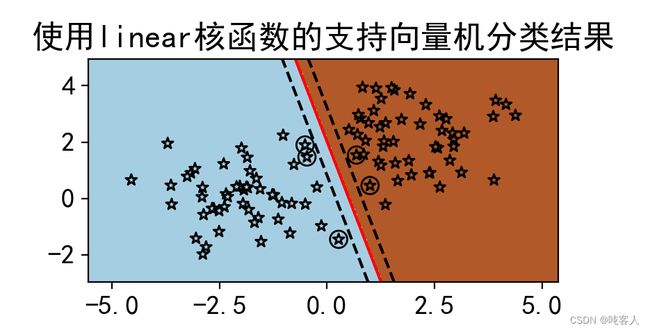
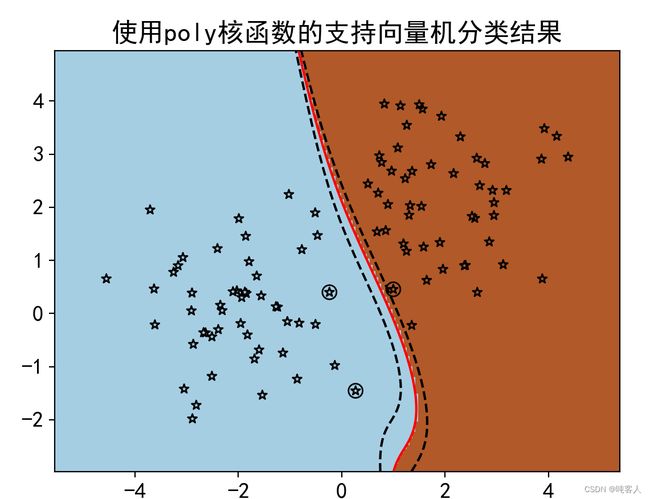
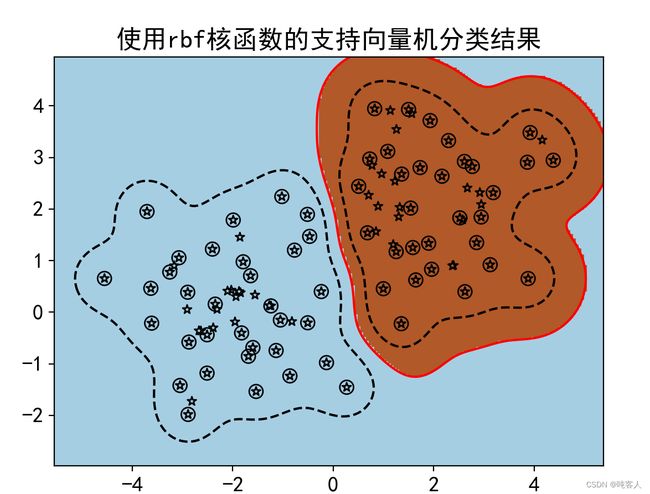
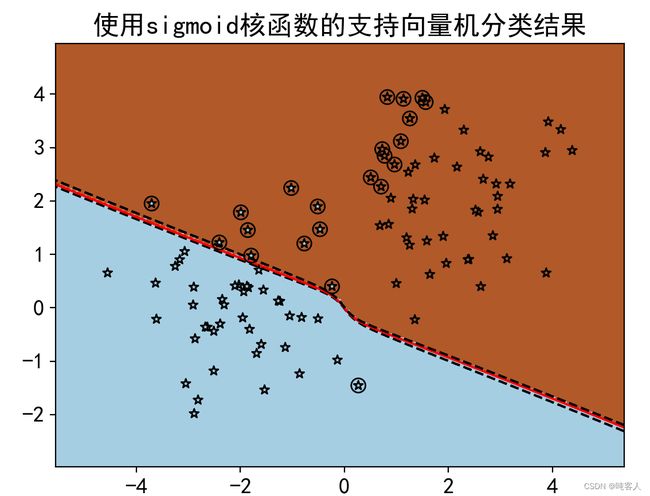
    title='使用'+kernel+'核函数的支持向量机分类结果'
    plt.title(title)#添加标题\n",
    #使用分类模型进行预测\n",
    print('使用',kernel,'核函数预测样本(3,3)属于类：',clf.predict([[3, 3]]))
    print('使用',kernel,'核函数预测样本(-3,3)属于类：',clf.predict([[-3, 3]]))
    plt.show()

本例使用make_blob()方法生成具有100 个样本，2 个特征的二元分类数据集
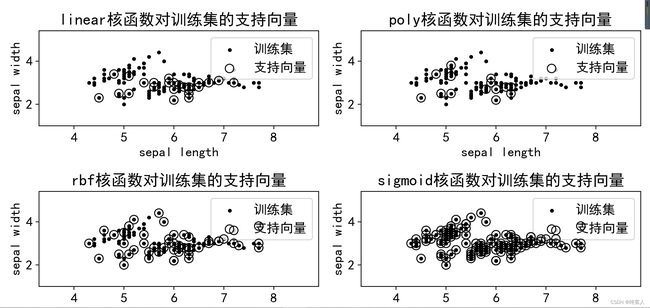
循环体具有核函数类型kernel和子图索引i共2个循环变量，因此使用了zip()方法。zip()方法将两个变量打包，每个变量均可以从中遍历自己的取值。4种核函数的分类表明，多项式核和线性核的分类效果最好。径向基和分类效果最差，它几乎把所有的训练样本都作为支持向量，这就失去了分类超平面仅有少数向量决定的初衷。
00

import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm, datasets
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.model_selection import train_test_split
iris = datasets.load_iris()
# 取全部4列作为特征属性\n",
X = iris.data
y = iris.target
X_train,X_test, y_train,y_test = train_test_split(
    X,y,train_size = 0.8,random_state = 42)

x_min,x_max=np.min(X[:,0])-1,np.max(X[:,0])+1
y_min,y_max=np.min(X[:,1])-1,np.max(X[:,1])+1
#可视化训练集（特征0,1）、支持向量\n",
plt.rc('font', size=14)#设置图中字号大小\n",
plt.rcParams['font.sans-serif'] = 'SimHei'#设置字体为SimHei显示中文\n",
plt.rcParams['axes.unicode_minus']=False#坐标轴刻度显示负号\n",
p=plt.figure(figsize=(12, 8))
kernels=['linear', 'poly', 'rbf','sigmoid']
figNum=[1,2,3,4]
for kernel,i in zip(kernels,figNum):#zip()用于非嵌套的多个变量的循环\n",
    #使用支持向量机进行训练\n",
    clf = svm.SVC(kernel=kernel,gamma=2)
    clf.fit(X_train, y_train)
    #y_pred = clf_svm.predict(X_test)\n",
    # 使用支持向量机进行训练\n",
    #可视化，获得支持向量，以特征0和1绘制其散点图，默认以圆圈表示\n",
    ax1 = p.add_subplot(2,2,i)
    #绘制训练集原始数据散点图，以表示\n",
    plt.scatter(X_train[:, 0], X_train[:, 1], c='k',marker='.')
    plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], s=80,
                facecolors='none', zorder=10, edgecolors='k')
    #对XX,YY规定的平面设置坐标轴刻度范围\n",
    plt.xlim(x_min, x_max)
    plt.ylim(y_min, y_max)
    plt.xlabel('sepal length')
    plt.ylabel('sepal width')
    plt.legend(['训练集','支持向量'])
    title=kernel+'核函数对训练集的支持向量'
    plt.title(title)#添加标题\n",
p.tight_layout()#调整空白，避免子图重叠\n",
# plt.show()

#可视化测试集、支持向量、分类错误的样本（特征0,1）\n",
p=plt.figure(figsize=(12, 8))
kernels=['linear', 'poly', 'rbf','sigmoid']
figNum=[1,2,3,4]
for kernel,i in zip(kernels,figNum):#zip()用于非嵌套的多个变量的循环\n",
    clf = svm.SVC(kernel=kernel,gamma=2)
    clf.fit(X_train, y_train)
    y_test_pred=clf.predict(X_test)#使用分类模型对测试集进行预测\n",
    #可视化，获得支持向量，以特征0和1绘制其散点图，默认以圆圈表示\n",
    ax1 = p.add_subplot(2,2,i)
    #绘制原始数据散点图\n",
    plt.scatter(X_test[:, 0], X_test[:, 1], c='k',marker='.')
    #获得支持向量，绘制其散点图，默认以圆圈表示\n",
    plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], s=80,
                facecolors='none', zorder=10, edgecolors='k')
    y_wrong=np.where(y_test_pred!=y_test)#获得分类错误的样本索引\n",
    #绘制测试集错误分类样本\n",
    plt.scatter(X_test[y_wrong, 0], X_test[y_wrong, 1], marker='v')
    plt.legend(['测试集','支持向量','错误分类'])
    plt.xlim(x_min, x_max)
    plt.ylim(y_min, y_max)
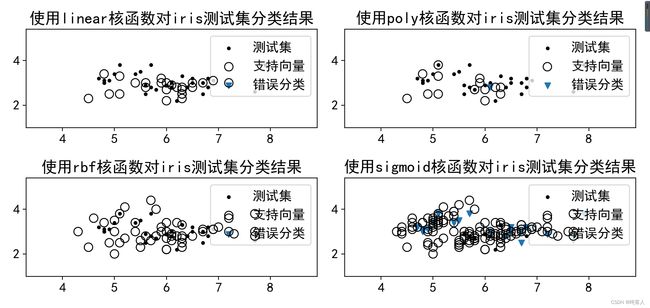
    title='使用'+kernel+'核函数对iris测试集分类结果'
    plt.title(title)#添加标题\n
p.tight_layout()#调整空白，避免子图重叠\n"
plt.show()

#可视化测试集、支持向量、分类错误的样本（特征2,3）\n",
p=plt.figure(figsize=(12, 8))
kernels=['linear', 'poly', 'rbf','sigmoid']
figNum=[1,2,3,4]
for kernel,i in zip(kernels,figNum):#zip()用于非嵌套的多个变量的循环\n",
    clf = svm.SVC(kernel=kernel,gamma=2)
    clf.fit(X_train, y_train)
    y_test_pred=clf.predict(X_test)#使用分类模型对测试集进行预测\n",
    #可视化，获得支持向量，以特征0和1绘制其散点图，默认以圆圈表示\n",
    ax1 = p.add_subplot(2,2,i)
    #绘制原始数据散点图\n",
    plt.scatter(X_test[:, 2], X_test[:, 3], c='k',marker='.')
    #获得支持向量，绘制其散点图，默认以圆圈表示\n",
    plt.scatter(clf.support_vectors_[:, 2], clf.support_vectors_[:, 3], s=80,
                facecolors='none', zorder=10, edgecolors='k')
    y_wrong=np.where(y_test_pred!=y_test)#获得分类错误的样本索引\n",
    #绘制测试集错误分类样本\n",
    plt.scatter(X_test[y_wrong, 2], X_test[y_wrong, 3], marker='v')
    plt.legend(['测试集','支持向量','错误分类'])
    #plt.xlim(x_min, x_max)\n",
    #plt.ylim(y_min, y_max)\n",
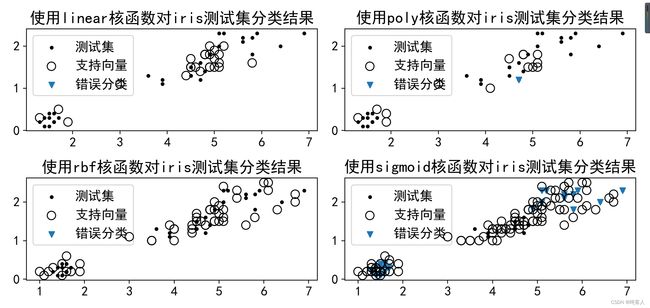
    title='使用'+kernel+'核函数对iris测试集分类结果'
    plt.title(title)#添加标题\n",
p.tight_layout()#调整空白，避免子图重叠\n",
plt.show()

使用将数据集拆分为数据集和训练集，以核函数类型和子图索引为变量。构造循环体。再循环体内形成svm.SVC()的实例clf,同时使用kernel参数传入函数模型，使用fit 方法拟合训练集，拟合模型时使用了全部4个特征。可视化时只选取了两个特征，便于绘制二维散点图。使用clf调用方法预测测试集。