【weka】决策树C4.5
参考
【1】C4.5算法详解(非常仔细)
【2】用 WEKA 进行数据挖掘,第 2 部分
【3】weka算法参数整理
【4】机器学习工具WEKA使用总结,包括算法选择、参数优化、属性选择
文章目录
- 参考
- 1 算法原理
-
- 1.1 计算类别信息熵
- 1.2 计算每个属性的信息熵
- 1.3 计算信息增益
- 1.4 计算属性分裂信息度量
- 1.5 计算信息增益率
- 2 weka上的实现
-
- 2.1 WEKA 数据集
- 2.2 在 WEKA 内进行分类
1 算法原理
首先,C4.5是决策树算法的一种。决策树算法作为一种分类算法,目标就是将具有p维特征的n个样本分到c个类别中去。相当于做一个投影,c=f(n),将样本经过一种变换赋予一种类别标签。决策树为了达到这一目的,可以把分类的过程表示成一棵树,每次通过选择一个特征pi来进行分叉。
那么怎样选择分叉的特征呢?每一次分叉选择哪个特征对样本进行划分可以最快最准确的对样本分类呢?不同的决策树算法有着不同的特征选择方案。
- ID3用信息增益
- C4.5用信息增益率
- CART用gini系数
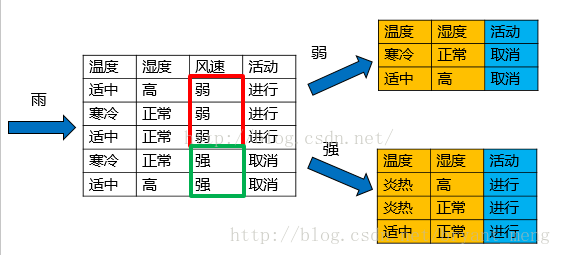
上述数据集有四个属性,属性集合
A={ 天气,温度,湿度,风速}
类别标签有两个
类别集合L={进行,取消}
1.1 计算类别信息熵
类别信息熵表示的是所有样本中各种类别出现的不确定性之和。根据熵的概念,熵越大,不确定性就越大,把事情搞清楚所需要的信息量就越多。
![]()
1.2 计算每个属性的信息熵
每个属性的信息熵相当于一种条件熵。他表示的是在某种属性的条件下,各种类别出现的不确定性之和。属性的信息熵越大,表示这个属性中拥有的样本类别越不“纯”。

1.3 计算信息增益
信息增益的 = 熵 - 条件熵,在这里就是 类别信息熵 - 属性信息熵,它表示的是信息不确定性减少的程度。如果一个属性的信息增益越大,就表示用这个属性进行样本划分可以更好的减少划分后样本的不确定性,当然,选择该属性就可以更快更好地完成我们的分类目标。
但是我们假设这样的情况,每个属性中每种类别都只有一个样本,那这样属性信息熵就等于零,根据信息增益就无法选择出有效分类特征。所以,C4.5选择使用信息增益率对ID3进行改进。
1.4 计算属性分裂信息度量
用分裂信息度量来考虑某种属性进行分裂时分支的数量信息和尺寸信息,我们把这些信息称为属性的内在信息(instrisic information)。信息增益率用信息增益 / 内在信息,会导致属性的重要性随着内在信息的增大而减小(也就是说,如果这个属性本身不确定性就很大,那我就越不倾向于选取它),这样算是对单纯用信息增益有所补偿。

1.5 计算信息增益率
IGR(天气) = Gain(天气)/ H(天气)=0.246 / 1.577 = 0.155
IGR(温度) = Gain(温度)/ H(温度)=0.029 / 1.556 = 0.0186
IGR(湿度) = Gain(湿度)/ H(湿度)=0.151 / 1.0 = 0.151
IGR(风速) = Gain(风速)/ H(风速)=0.048 / 0.985 = 0.048
天气的信息增益率最高,选择天气为分裂属性。发现分裂了之后,天气是“阴”的条件下,类别是”纯“的,所以把它定义为叶子节点,选择不“纯”的结点继续分裂。
在子结点当中重复过程1~5。
2 weka上的实现
这个简单的分类树试图回答这个问题:“您理解分类树么?”在每个节点,您都会回答这个问题并继续沿着分支下移,直到您到达一个回答了是或不是的叶子节点。 这个模型可用于任何未知的数据实例,来预测这个未知数据实例是否通过只询问两个简单问题就能理解分类树。这看上去像是分类树的一大优势 — 它无需有关数据的大量信息就能创建一个十分准确且信息丰富的树。
分类树的一个重要概念非常类似于我们在 用 WEKA 进行数据挖掘,通常会把整个训练集分成两个部分:拿数据的约 60-80 % 放入我们的训练集,用来生成模型;然后拿剩下的数据放入一个测试集,在模型生成后,立即用其来测试我们模型的准确性。
那么这个额外的步骤为什么在此模型中如此重要呢?这个问题就是所谓的过拟合:如果我们提供过多 数据用于模型创建,我们的模型虽然会被完美创建,但只针对的是该数据。请记住:我们想使用此模型来预测未来的未知数;我们不是想使用此模型来准确地预测我们已经知道的值。这就是为什么我们要创建一个测试集。在创建了模型后,我们要进行检查以确保我们所创建模型的准确性不会在测试集降低。这就保证了我们的模型会准确地预测出未来的未知值。使用 WEKA 会看到它的实际效果。
这还引出了分类树的另一个重要概念:修剪。修剪 正如其名字所指,意思是删减分类树的枝条。那么为什么有人会想要将信息从分类树中删除呢?还是因为过拟合的缘故。随着数据集的增大以及属性数量的增长,我们所创建的树就会越来越复杂。理论上讲,一个树可以具有 leaves = (rows * attributes)。但那又有何益处呢?就预测未来的未知数而言,它根本帮不到我们,因它只适于我们现有的训练数据。因此我们需要的是一种平衡。我们想要我们的树尽量简单,节点和枝叶尽量少。同时我们还想要它尽量地准确。这就需要进行权衡,我们不久就会看到。
在使用 WEKA 前,有关分类我还想指出最后一点,那就是假正和假负。假正指的是这样的一个数据实例:我们创建的这个模型预测它应该是正的,但事实相反,实际值却是负的。同样地,假负指的是这样一个数据实例:我们创建的这个模型预测它应该是负的,但事实相反,实际值却是正的。
这些错误表明在我们的模型中出了问题,我们的模型正在错误地分类某些数据。虽然可能会出现不正确的分类,但可接受的错误百分比由模型创建者决定。比如,如果是在医院里测试心脏监视器,很显然,将需要极低的错误百分比。而如果您只是在有关数据挖掘的文章中挖掘一些虚构的数据,那么错误率可以更高一些。为了使之更进一步,还需要决定可以接受的假负与假正的百分比率是多少。我立即想到的一个例子就是垃圾邮件模型:一个假正(一个真邮件被标记为了垃圾邮件)要比假负(一个垃圾消息未被标记为垃圾邮件)更具破坏性。在像这样的例子中,就可以判断假负:假正的比率最低为 100:1 才是可以接受的。
好了,对于分类树的背景和技术方面的介绍已经够多了。让我们现在开始获得一些真正的数据并将其带入 WEKA。
2.1 WEKA 数据集
我们用于分类示例的数据集所围绕的仍然是我们虚构的 BMW 经销店。这个经销店正在启动一个推销计划,试图向其老客户推销两年延保。这个经销店过去曾做过类似的计划并从过去的销售中收集了 4,500 个数据点。数据集中的属性有:
- 收入水平 [0=$0-$30k, 1=$31k-$40k, 2=$41k-$60k, 3=$61k-$75k,
4=$76k-$100k, 5=$101k-$150k, 6=$151k-$500k, 7=$501k+] - 第一辆 BMW 购买的年/月
- 最近的 BMW 购买的年/月
- 是否过去曾响应过延保计划
让我们来看看在这个例子中使用的 Attribute-Relation File Format (ARFF)。
@relation bmwreponses
@attribute IncomeBracket {0,1,2,3,4,5,6,7}
@attribute FirstPurchase numeric
@attribute LastPurchase numeric
@attribute responded {1,0}
@data
4,200210,200601,0
5,200301,200601,1
6,200411,200601,0
5,199609,200603,0
2.2 在 WEKA 内进行分类
使用数据文件 bmw-training.arff (参见 下载)
请注意:这个文件只包含经销店记录内的这 4,500 个记录中的 3,000 个。我们需要分割我们的记录以便某些数据实例被用来创建模型,某些被用来测试模型以确保没有过拟合。
下载数据集后,打开WEKA软件,需要预先配置好java。软件的操作说明可以参考这篇博客 机器学习:WEKA的应用之 J48(C4.5)
我们选择 Classify 选项卡,然后选择 trees 节点,然后是 J48 叶子(我不知道为何这就是正式的名称,不过还是接受吧)。
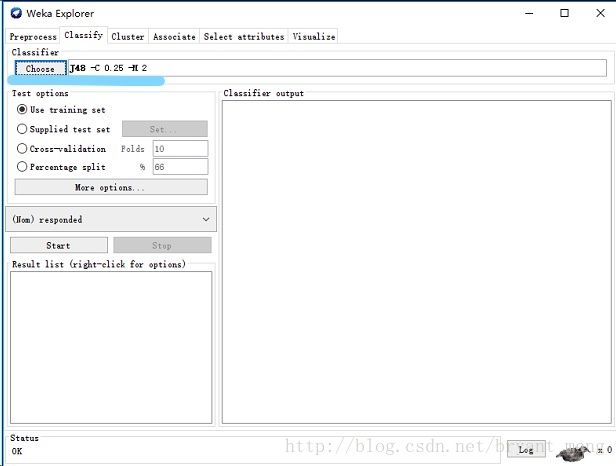
至此,我们已经准备好可以在 WEKA 内创建我们的模型了。请确保 Use training set 被选中以便我们使用刚刚加载的这个数据集来创建模型。单击 Start 并让 WEKA 运行。模型的输出结果如下。
=== Run information ===
Scheme: weka.classifiers.trees.J48 -C 0.25 -M 2
Relation: bmwreponses
Instances: 3000
Attributes: 4
IncomeBracket
FirstPurchase
LastPurchase
responded
Test mode: evaluate on training data
=== Classifier model (full training set) ===
J48 pruned tree
------------------
FirstPurchase <= 200011
| IncomeBracket = 0: 1 (271.0/114.0)
| IncomeBracket = 1
| | LastPurchase <= 200512: 0 (69.0/21.0)
| | LastPurchase > 200512: 1 (69.0/27.0)
| IncomeBracket = 2: 1 (194.0/84.0)
| IncomeBracket = 3: 1 (109.0/38.0)
| IncomeBracket = 4
| | LastPurchase <= 200511: 0 (54.0/22.0)
| | LastPurchase > 200511: 1 (105.0/40.0)
| IncomeBracket = 5
| | LastPurchase <= 200505
| | | LastPurchase <= 200504: 0 (8.0)
| | | LastPurchase > 200504
| | | | FirstPurchase <= 199712: 1 (2.0)
| | | | FirstPurchase > 199712: 0 (3.0)
| | LastPurchase > 200505: 1 (185.0/78.0)
| IncomeBracket = 6
| | LastPurchase <= 200507
| | | FirstPurchase <= 199812: 0 (8.0)
| | | FirstPurchase > 199812
| | | | FirstPurchase <= 200001: 1 (4.0/1.0)
| | | | FirstPurchase > 200001: 0 (3.0)
| | LastPurchase > 200507: 1 (107.0/43.0)
| IncomeBracket = 7: 1 (115.0/40.0)
FirstPurchase > 200011
| IncomeBracket = 0
| | FirstPurchase <= 200412: 1 (297.0/135.0)
| | FirstPurchase > 200412: 0 (113.0/41.0)
| IncomeBracket = 1: 0 (122.0/51.0)
| IncomeBracket = 2: 0 (196.0/79.0)
| IncomeBracket = 3: 1 (139.0/69.0)
| IncomeBracket = 4: 0 (221.0/98.0)
| IncomeBracket = 5
| | LastPurchase <= 200512: 0 (177.0/77.0)
| | LastPurchase > 200512
| | | FirstPurchase <= 200306: 0 (46.0/17.0)
| | | FirstPurchase > 200306: 1 (88.0/30.0)
| IncomeBracket = 6: 0 (143.0/59.0)
| IncomeBracket = 7
| | LastPurchase <= 200508: 1 (34.0/11.0)
| | LastPurchase > 200508: 0 (118.0/51.0)
Number of Leaves : 28
Size of the tree : 43
Time taken to build model: 0.08 seconds
=== Evaluation on training set ===
Time taken to test model on training data: 0.06 seconds
=== Summary ===
Correctly Classified Instances 1774 59.1333 %
Incorrectly Classified Instances 1226 40.8667 %
Kappa statistic 0.1807
Mean absolute error 0.4773
Root mean squared error 0.4885
Relative absolute error 95.4768 %
Root relative squared error 97.7122 %
Coverage of cases (0.95 level) 100 %
Mean rel. region size (0.95 level) 99.6 %
Total Number of Instances 3000
=== Detailed Accuracy By Class ===
TP Rate FP Rate Precision Recall F-Measure MCC ROC Area PRC Area Class
0.662 0.481 0.587 0.662 0.622 0.182 0.616 0.599 1
0.519 0.338 0.597 0.519 0.555 0.182 0.616 0.596 0
Weighted Avg. 0.591 0.411 0.592 0.591 0.589 0.182 0.616 0.597
=== Confusion Matrix ===
a b <-- classified as
1009 516 | a = 1
710 765 | b = 0
上述这些数字是什么意思?我们怎么才能知道这是一个好的模型?我们应该寻找的这个所谓的“树”在哪里?这些问题问得很好。让我们逐一回答:
- 这些数字是什么意思? 这里应该关注的重要数字是“Correctly Classified Instances”(59.1 %)与“Incorrectly Classified Instances”(40.9 %)旁边的这些数字。其他的重要数字还有“ROC Area”列第一行的这个数字(0.616);我稍候会详细解释这个数字,目前只需记住即可。最后,在“Confusion Matrix”中,显示了假正和假负的数量。在这个矩阵中,假正为 516,假负为 710。
- 我们怎么才能知道这是一个好的模型? 由于准确率仅为 59.1 %,我不得不承认经初步分析后,这不是一个非常好的模型。
- 这个所谓的“树”在哪里? 要看到这个树,可右键单击刚刚创建的这个模型。在弹出菜单中,选择 Visualize tree。之后,就会看到我们所创建的这个分类树,虽然在本例中,可视树不能提供任何帮助。我们的树如图 3 所示。看到这个树的另一种方式是在 Classifier Output 内往高处看,其中的文本输出显示了具有节点和叶子的整个树。
还有最后一个步骤,就是验证我们的分类树,这需要贯穿模型运行我们的测试集并确保我们模型的准确性在测试集时与在训练集时相差不远。为此,在 Test options 内,选择 Supplied test set 单选按钮并单击 Set。选择文件 bmw-test.arff,内含 1,500 条记录,而这些记录在我们用来创建模型的训练集中是没有的。当我们这次单击 Start 时,WEKA 将会贯穿我们已经创建的这个模型运行测试数据集并会让我们知道模型的情况。让我们现在单击 Start。如下是输出。
=== Run information ===
Scheme: weka.classifiers.trees.J48 -C 0.25 -M 2
Relation: bmwreponses
Instances: 3000
Attributes: 4
IncomeBracket
FirstPurchase
LastPurchase
responded
Test mode: user supplied test set: size unknown (reading incrementally)
=== Classifier model (full training set) ===
J48 pruned tree
------------------
FirstPurchase <= 200011
| IncomeBracket = 0: 1 (271.0/114.0)
| IncomeBracket = 1
| | LastPurchase <= 200512: 0 (69.0/21.0)
| | LastPurchase > 200512: 1 (69.0/27.0)
| IncomeBracket = 2: 1 (194.0/84.0)
| IncomeBracket = 3: 1 (109.0/38.0)
| IncomeBracket = 4
| | LastPurchase <= 200511: 0 (54.0/22.0)
| | LastPurchase > 200511: 1 (105.0/40.0)
| IncomeBracket = 5
| | LastPurchase <= 200505
| | | LastPurchase <= 200504: 0 (8.0)
| | | LastPurchase > 200504
| | | | FirstPurchase <= 199712: 1 (2.0)
| | | | FirstPurchase > 199712: 0 (3.0)
| | LastPurchase > 200505: 1 (185.0/78.0)
| IncomeBracket = 6
| | LastPurchase <= 200507
| | | FirstPurchase <= 199812: 0 (8.0)
| | | FirstPurchase > 199812
| | | | FirstPurchase <= 200001: 1 (4.0/1.0)
| | | | FirstPurchase > 200001: 0 (3.0)
| | LastPurchase > 200507: 1 (107.0/43.0)
| IncomeBracket = 7: 1 (115.0/40.0)
FirstPurchase > 200011
| IncomeBracket = 0
| | FirstPurchase <= 200412: 1 (297.0/135.0)
| | FirstPurchase > 200412: 0 (113.0/41.0)
| IncomeBracket = 1: 0 (122.0/51.0)
| IncomeBracket = 2: 0 (196.0/79.0)
| IncomeBracket = 3: 1 (139.0/69.0)
| IncomeBracket = 4: 0 (221.0/98.0)
| IncomeBracket = 5
| | LastPurchase <= 200512: 0 (177.0/77.0)
| | LastPurchase > 200512
| | | FirstPurchase <= 200306: 0 (46.0/17.0)
| | | FirstPurchase > 200306: 1 (88.0/30.0)
| IncomeBracket = 6: 0 (143.0/59.0)
| IncomeBracket = 7
| | LastPurchase <= 200508: 1 (34.0/11.0)
| | LastPurchase > 200508: 0 (118.0/51.0)
Number of Leaves : 28
Size of the tree : 43
Time taken to build model: 0.02 seconds
=== Evaluation on test set ===
Time taken to test model on supplied test set: 0.02 seconds
=== Summary ===
Correctly Classified Instances 835 55.6667 %
Incorrectly Classified Instances 665 44.3333 %
Kappa statistic 0.1156
Mean absolute error 0.4891
Root mean squared error 0.5
Relative absolute error 97.79 %
Root relative squared error 99.9582 %
Coverage of cases (0.95 level) 99.6 %
Mean rel. region size (0.95 level) 99.6 %
Total Number of Instances 1500
=== Detailed Accuracy By Class ===
TP Rate FP Rate Precision Recall F-Measure MCC ROC Area PRC Area Class
0.622 0.506 0.541 0.622 0.579 0.117 0.564 0.527 1
0.494 0.378 0.576 0.494 0.532 0.117 0.564 0.565 0
Weighted Avg. 0.557 0.441 0.559 0.557 0.555 0.117 0.564 0.546
=== Confusion Matrix ===
a b <-- classified as
457 278 | a = 1
387 378 | b = 0
对比这个测试集的“Correctly Classified Instances”(55.7 %)与训练集的“Correctly Classified Instances”(59.1 %),我们看到此模型的准确性非常接近,这表明此模型不会在应用未知数据或未来数据时,发生故障。
不过,由于模型的准确性很差,只能正确地分类 60 % 的数据记录,因此我们可以后退一步说:“哦,这个模型一点都不好。其准确性勉强超过 50 %,我随便猜猜,也能得到这样的准确性。”这完全正确。这也是我想审慎地告诉大家的一点:有时候,将数据挖掘算法应用到数据集有可能会生成一个糟糕的模型。这一点在这里尤其准确,并且它是故意的。
我本想带您亲历用适合于分类模型的数据生成一个分类树的全过程。然而,我们从 WEKA 获得的结果表明我们错了。我们在这里本应选择的并非 分类树。我们所创建的这个模型不能告诉我们任何信息,并且如果我们使用它,我们可能会做出错误的决策并浪费钱财。
那么这是不是意味着该数据无法被挖掘呢?当然不是,只不过需要使用另一种数据挖掘方法:最近邻模型,该模型会在本系列的后续文章中讨论,它使用相同的数据集,却能创建一个准确性超过 88 % 的模型。它旨在强调一点:那就是必须为数据选择合适的模型才能得到有意义的信息。