WaPIRL: 基于自监督表示学习的晶圆图缺陷模式分类模型

Self-Supervised Representation Learning for Wafer Bin Map Defect Pattern Classification(基于自监督表示学习的晶圆图缺陷模式分类)

1. PIRL模型

1.1 PIRL模型的思想：

PIRL: Pretext-Invariant Representations Learning，出自论文Self-Supervised Learning of Pretext-Invariant Representations(CVPR 2020)

该算法是一种对比自监督学习的方法，其特别之处在于Pretext Invariant Representations（预任务不变表征），即定义一个表征网络$N$；图像$A$经过$N$得其表征为$A_f$，对图像$A$处理（如下图所示的拼图重排）后得图像$a$经过$N$得其表征为$a_f$；经过训练后使得$A_f$和$a_f$很相近，接近于没怎么变化，同时$A_f$和$x_f$（x≠a）却相差很大。

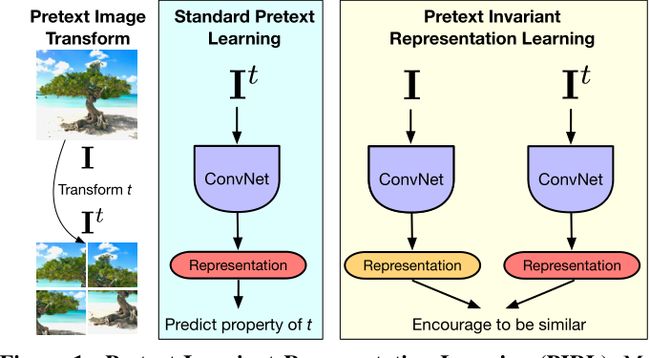
其思想为：无论选择什么样的pretext task（预任务，也有人叫代理任务或前置任务），如果图像相同，即使转换后也不会改变图像的语义信息，因此让同一图片转换前后的表征相同。更多有关pretext task的概念可见：神经网络前置任务（pretext task）有什么作用？

1.2 PIRL的模型结构：

图像$I$经res5网络（即ResNet-50的前5层），然后以此进行一次average pooling和一次线性映射得到一个128维的向量表征$f(v_I)$；

图像$I$分为3块拼图构成$I^t$，每块拼图都分别经res5网络处理后进行一次average pooling， 然后分别进行一次线性映射得到3个总共128维的向量，将这3个向量随机排序后合并，然后再进行一次线性映射得到一个128维的向量表征$g(v_I)$；

$M$ Memory Bank和MOCO中的Memory Bank类似，其保存了所有图像I的$f(v_I)$表征；针对每一张图像$I$在多轮训练时，每一轮训练都会生成一次$f(v_I)$，而Memory Bank中得$m_I$是多轮训练得到的$f(v_I)$的指数移动平均值。在对比学习中常被使用到的噪声对比估计(NCE)损失在计算中往往需要很多的负例，这里的Memory Bank的作用是存储大量的负例样本。更多关于PIRL模型的细节可见下文：[Self-Supervised Learning–PIRL(自监督学习–预任务不变表征学习)](Self-Supervised Learning–PIRL(自监督学习–预任务不变表征学习) - 知乎 (zhihu.com))

2. WaPIRL模型

WaPIRL是首次在半导体领域应用PIRL模型的一种方法，实现对半导体产业中重要的晶圆图WBM(wafer bin map)缺陷检测。

在工业品缺陷检测的场景中，由于缺陷样本少，往往得到的有标签的缺陷数据样本在样本量和图像质量上都非常受限。这篇文章提出的方法是：先用自监督的方式充分利用无标签的缺陷样本来预先学习被检测对象丰富的视觉表示，以实现数据高效的晶圆图缺陷模式分类；之后用少量有标签的缺陷样本对网络进行微调来实现下游的缺陷分类任务。前期从无标签的数据中自监督学习迁移的表现对后期缺陷样本分类任务有很大帮助，文中的实验证明此方法在少样本的情况下有很大的优越性。

2.1 WaPIRL模型结构

WaPIRL的模型训练要经过两个阶段: 1.自监督的预训练阶段; 2.监督的微调阶段。

2.1.1 自监督预训练

自监督预训练阶段的目标是学习晶圆图丰富的特征表示，这些特征表示体现了WBMs之间的语义相似性。完成这个目标的方式是最小化对比损失函数使得未经数据增强的WBM样本和数据增强后的WBM样本(正例)尽量接近。文中把这种方法称为”面向晶圆的预任务不变表征学习“(WaPIRL)。

WaPIRL的模型框架分为5个部分：数据增强函数$t(\cdot )$，编码器网络$f_{\theta }(\cdot )$，projection head $g_{\varphi }(\cdot )$，内存银行(memory bank) $M$，自监督对比损失函数${\mathcal{L}}_{SSCL}$。

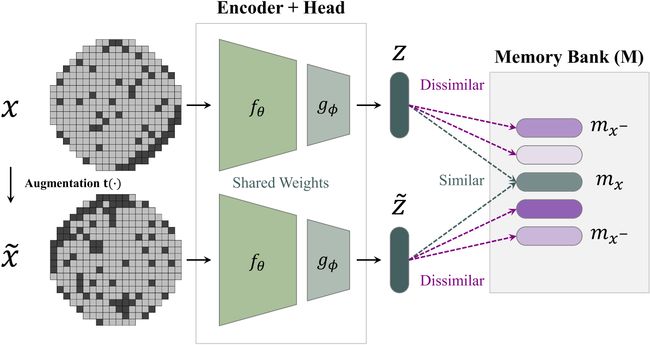
数据增强函数$t(\cdot )$用来生成用于对比学习的WBM正例对。给定一个原始的，未经数据增强的WBM数据样本$x_i$，用数据增强函数$t(\cdot )$将WBM样本转换为一个随机数据增强的版本${\tilde{x}}_i=t\left(x_i\right)$，文中采用了5种不同的数据增强方式：裁剪，cutout，增加噪声，旋转和平移。

文中的编码器网络$f_{\theta }(\cdot )$使用了4种不同的CNN模型结构：AlexNet，VGG16，ResNet-18和ResNet-50。对于AlexNet和VGG16，将全连接层替换成全局平均池化层来得到一个$D_f$维的表征向量。对于已经有全局平均池化层的ResNet-18和ResNet-50网络，只需要将最后的全连接层移除掉。经过如此调整，$D_f$由最后的卷积层对应的feature maps数量决定。

projection head $g_{\varphi }(\cdot )$接受来自CNN编码器网络$f_{\theta }(\cdot )$输出的表示向量$v_i$和${\tilde{v}}_i$，并将它们映射到$D_g$维度的嵌入向量$z_i=g_{\varphi }\left(v_i\right)\in {\mathbb{R}}^{D_g}$和${\tilde{z}}_i=g_{\varphi }\left({\tilde{v}}_i\right)\in {\mathbb{R}}^{D_g}$，实验中的projection head $g_{\varphi }(\cdot )$使用一层全连接层，固定其输出维度$D_g$为128。输出的嵌入向量经过$l_2$归一化后使得$\left|z_i\right|=\left|{\tilde{z}}_i\right|=1$，约束包含图像表征信息的嵌入向量在一个单位超球面上。归一化操作使得嵌入向量之间的相似程度可以简单地用它们的内积来衡量(余弦相似度)。这里需要注意的是projection head仅在自监督预训练阶段计算损失时有用，在监督的微调阶段会被替换成线性层和softmax层以实现下游的分类任务。

内存银行$M$保存每个无标签的训练样本$x_i$在不同epoch下经过编码器网络$f_{\theta }(\cdot )$和projection head $g_{\varphi }(\cdot )$输出的嵌入向量$z_i=g_{\varphi }\left(f_{\theta }\left(x_i\right)\right)$作指数移动平均(EMA)的结果。其作用在于减轻对比学习中采样负例带来的计算负担。$M$中第$i$个样本$m_i\in {\mathbb{R}}^{D_g}$的数学定义如下：
$$m_i\leftarrow \gamma m_i+(1-\gamma )z_i$$
实验中取$\gamma =0.5$给之前和现在的状态分配相同的权重。这里的内存银行$M$和MoCo中的相似，其中的元素$m_i$可以被用作对比学习中的负例样本来使用，EMA的作用是在参数更新的同时构建更加稳定的模型参数。如果$M$中的元素$m_i$只是当前epoch下每个样本对应的嵌入向量，而与之前的epoch无关，则对负例样本的采样将很大程度上取决于该epoch下编码器网络$f_{\theta }(\cdot )$，缺少一致性，这样一来训练得到的模型参数不够稳定。而对$m_i$进行EMA的更新可以引入之前多个epoch下样本对应的嵌入向量，增加负例样本采样的一致性，得到更加稳定的模型参数。

给定一对正例样本的嵌入向量$(z_i,{\tilde{z}}_i)$，我们的目标是通过最小化NCE损失函数最大化它们的相似性，噪声对比估计NCE损失的使用将分布$p(z_i,{\tilde{z}}_i)$表示为两个正例嵌入向量$(z_i,{\tilde{z}}_i)$是否来自同一分布的二分类任务的概率。对于第$i$个样本，其最一般形式的分布$p(z_i,{\tilde{z}}_i)$函数可表示如下。
$$p\left(z_i,{\tilde{z}}_i\right)=\frac{\exp \left(\frac{s\left(z_i,{\tilde{z}}_i\right)}{\tau }\right)}{\exp \left(\frac{s\left(z_i,{\tilde{z}}_i\right)}{\tau }\right)+{\sum }_{j\in \mathcal{D}-\{i\}}\exp \left(\frac{s\left(z_i,z_j\right)}{\tau }\right)}$$
以上公式中的$s(\cdot ,\cdot )$表示内积运算(向量模长为1时等同于它们的余弦相似度)，温度$\tau$起到控制向量之间相似度的数值规模的平滑作用。最大化上式的似然函数的作用是找到合适的编码器网络参数使得来自同一WBM缺陷图像的正例样本对的嵌入向量$(z_i,{\tilde{z}}_i)$之间的相似程度最大，来自不同WBM缺陷图像的负例样本对嵌入向量之间的相似程度最小。上式中分母的累加项由于包含了所有负例样本，其计算量是十分巨大的。为了减少计算量，实验中只随机采样$K$(实验中取5000)个负例样本，则上面的公式可以近似的表示为：
$$p\left(z_i,{\tilde{z}}_i\right)=\frac{\exp \left(\frac{s\left(z_i,{\tilde{z}}_i\right)}{\tau }\right)}{\exp \left(\frac{s\left(z_i,{\tilde{z}}_i\right)}{\tau }\right)+{\sum }_{j\in {\mathcal{J}}_{-i}}\exp \left(\frac{s\left(z_i,z_j\right)}{\tau }\right)}$$
事实上，尽管只采样$K$个负例样本，但对这$K$个负例样本计算嵌入向量时仍然需要网络进行$K$次前向传播，其计算量仍然十分巨大。解决这个问题的办法是：用内存银行$M$中的$m_j$来代替$z_j$，上面的式子又可以表示为下面的形式。
$$p\left(z_i,m_i\right)=\frac{\exp \left(\frac{s\left(z_i,m_i\right)}{\tau }\right)}{\exp \left(\frac{s\left(z_i,m_i\right)}{\tau }\right)+{\sum }_{j\in {\mathcal{J}}_{-i}^K}\exp \left(\frac{s\left(z_i,m_j\right)}{\tau }\right)}$$
由以上方法定义的负对数似然NCE损失函数形式为：
$${\mathcal{L}}_{NCE}\left(z_i,m_i\right)=-\log \left(p\left(z_i,m_i\right)\right)$$
最后，文中定义的自监督对比损失函数${\mathcal{L}}_{SSCL}$，由两部分以上形式的NCE损失函数构成。
$${\mathcal{L}}_{SSCL}=\frac{1}{N_u}\sum _{i=1}^{N_u}\lambda {\mathcal{L}}_{NCE}\left(z_i,m_i\right)+(1-\lambda ){\mathcal{L}}_{NCE}\left({\tilde{z}}_i,m_i\right)$$
式中的$\lambda$取0到1之间的值，第一项的作用是使原始WBM样本的嵌入向量$z_i$与其内存银行$M$中的对应向量$m_i$最接近，而第二项的作用是让数据增强后的WBM样本的嵌入向量${\tilde{z}}_i$与$m_i$最接近。从三元组损失函数的角度来看，内存银行$M$中的记忆表示$m_i$起到锚点的作用，将$z_i$和${\tilde{z}}_i$拉得更近，同时推开$K$个反例样本。根据以往工作的经验，只需设置$\lambda =0.5$，以得到最佳性能。

2.1.2 监督微调训练

在自监督预训练阶段结束后，先去掉projection head $g_{\varphi }(\cdot )$，并替换成线性层$h_{\omega }(\cdot )$，随后是Softmax函数以将输出的Logits归一化为概率。在线性层之前，加入一个概率为0.5的dropout层以防止过拟合。此外，我们将标签平滑的方法应用原来one-hot编码标签，以减轻标记错误的噪声标签(noisy labels)的破坏影响。给定具有$C$个不同缺陷模式类别的$N_l$个有标签的 WBMs作为训练数据集，我们用于监督微调的损失函数${\mathcal{L}}_{SL}$是具有如下形式的标签平滑的分类交叉熵函数：
$${\mathcal{L}}_{SL}=-\sum _{i=1}^{N_l}\sum _{c=1}^C{\tilde{y}}_{i,c}\cdot \log {\hat{y}}_{i,c}$$
式中，${\tilde{y}}_{i,c}=(1-\alpha )\cdot y_{i,c}+\frac{\alpha }{C-1}\cdot \left(1-y_{i,c}\right)$为在$[0,1]$范围内的软标签，$\alpha \in [0,1]$为一个用于标签平滑的因子。模型预测的${\hat{y}}_{i,c}\in [0,1]$是第$i$个WBM样本属于$C$类的归一化概率。由上面的式子可知，$\alpha =0$时的情况为使用原始one-hot编码标签时的情况，根据PIRL中的实验设置，将$\alpha$设为0.1。

2.2 实验结果

文中在多组实验的微调阶段使用了不同的有标签的训练数据量，并将WaPIRL的分类性能与监督学习的方法(没有预训练)进行比较，以证明WaPIRL有效性。文中还将WaPIRL与其他方法的分类性能进行了比较。

2.2.1 WM-811K数据集

实验在WBM数据集WM-811K上评估了WaPIRL的性能，WM-811K包括从现实世界制造过程中获得的811457个样本。只有含有172950个样本的子集有人为标注的九个缺陷类别之一的标签，多达638507个样本是无标签的。

而且有标签的样本分布非常不平衡；占主导地位的缺陷类别占标签样本总量的85%。在这种严重的类别不平衡的情况下，监督学习模型容易在训练过程对主导的缺陷类别过拟合。考虑到神经网络优化过程中对数据批量处理的性质，实验中对网络接收的每一批样本进行重采样来缓解缺陷类别不均衡的问题。

WM-811K样本在正常的晶圆仓处设置值为1，失效的晶圆仓处设置值为2，无晶圆仓处设置值为0(指示圆形WBM区域之外的位置)。同时，数据集由不同空间分辨率的WBMs组成。训练的CNN需要固定的输入大小，实验中使用最近邻内插法将每个WBM样本的大小调整为96×96。

2.2.2 不同数据增强方式的效果

• 使用单一数据增强实验

实验表明，数据增强对提升分类性能的意义重大。在使用一种数据增强的实验中，裁剪(Crop)对实验效果的提升最大。在小量标签数据样本的情况下WaPIRL方法的提升更大，而且使用WaPIRL方法在不同有标签的数据量下均超过了有监督方法的Baseline。

• 两种数据增强混合使用

混合数据增强方式的实验结果与单一数据增强实验的结果一致，**裁剪(Crop)**对提高整体分类性能方面起着关键作用。

需要注意的是，针对不同的下游任务，数据增强方法一定要谨慎选择。如在某些诸如缺陷根本原因分析的下游任务中，某些数据增强方式可能是不合适的，因为它可能会通过损害WBMs的方向而无意中删除有价值的信息。而文中的实验只关注WBMs的缺陷分类，不用考虑这样的问题。

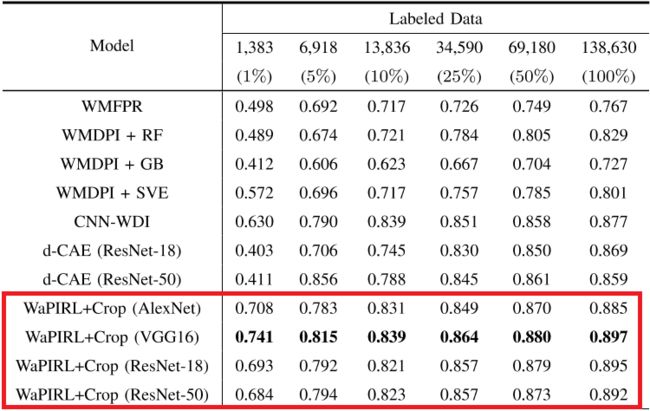
2.2.3 与其他方法的对比

与其他现有的方法作对比，文中提出的方法也展示出了最优的分类性能。