【论文串讲】从GPT和BERT到XLNet
“ 本文是本专栏即将发表的文本预训练系列里面的一个章节,主要讲了XLNet的思路和具体实现细节,之所以叫XLNet是因为它以Transformer- XL为基础。XLNet是一种广义的自回归预训练模型,它提出了Permuted Language Model的思路,将BERT和GPT的各自优点结合在一起。为了解决实现一个细节上的问题,它还创新地提出了“双流自注意力机制”。那么具体是怎么展开的,就来一起看看吧!。
”
作者:潘小小,字节跳动AI-Lab算法工程师,专注机器翻译,会讲法语,喜欢音乐,写文,记录,无人机航拍(刚入坑)。
本文涉及的论文链接: XLNet: Generalized Autoregressive Pretraining for Language Understanding(https://arxiv.org/abs/1906.08237)
「在开头先列出本文中涉及到的名词缩写:」
「LM」 : Language Model,语言模型
「AR」 : Auto-Regressive,自回归
「AE」 : Auto-Encoding,自编码
「MLM」 : Masked Language Model
「PLM」 : Permuted Language Model
「NLU」 : Natural Language Understanding
「NLG」 : Natural Language Generation
「1. GPT」
「关键词:」 单向信息,NLU的pretrain-finetune差异
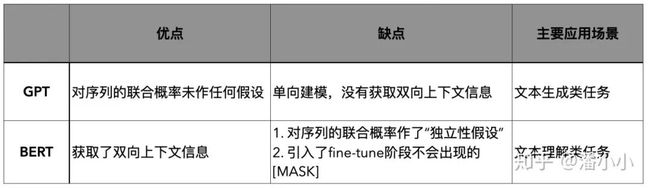
优化目标是单向(从左到右或者从右到左)建模序列的联合概率,是传统意义上的语言模型,后预测的词以先预测的词为条件,比较适合文本生成任务,但是缺陷是只使用了单向的语言表征信息,无法获取双向上下文信息表征,而文本理解任务中经常需要用到双向的上下文信息(比如,完形填空),因此,这就带来了pre- train阶段和下游任务的不一致。
「2. BERT」
「关键词:」 双向信息,独立性假设,NLG的pretrain-finetune差异
将一段序列部分“损坏”,优化目标是部分损坏的序列恢复到原始序列的独立概率之积。其优点是获取了双向上下文信息表征,缺点之一是引入了“ 「独立性假设」”,也即每一个被mask的token都是独立被重建的;缺点之二是预训练阶段的[MASK] token在下游任务的finetune中并没有出现过,这也会造成pretrain阶段和下游生成类任务的不一致。
如果当前token被mask,则 否则
为部分损坏的序列
**3. XLNet (AR + MLM - > PLM) **
GPT和BERT的对比如下图所示
「我们的核心的关注点是: 如何取两者之长,避两者之短」 。首先要提到的就是XLNet这篇工作:XLNet是一种广义的Auto- Regressive模型,它可以看作将序列的联合概率分布按照打乱的顺序重新因式分解,其将LM的 「顺序拆解推广到随机拆解」,token之间的自回归关系不再是基于在 「天然序列」 中的前后顺序,而是基于 「打乱后的序列」 中的前后顺序。
顺序拆解(左):
乱序拆解(右): ,( )
正是因为这种“打乱”(permutation)的机制,模型既可以保留AR的优点,规避AE的缺点(独立性假设;引入[MASK]),又可以保留AE的优点: 使得每个位置的token可以获取到双边的信息(因为序列被打乱了)。这样的建模方法,也叫做 「Permuted Language Model」(PLM)。
3.1 通过attention去实现Permutation
在具体的实现上,我们并不需要真正地去打乱序列的顺序,只需记住Transformer框架下的序列中token的位置和它对应的position encoding「唯一绑定」 (请参考 潘小小:【经典精读】Transformer模型深度解读 positional encoding那一节的内容)。所以,只需要设计合适的attention mask就可以实现对因式分解顺序的打乱。
论文里有这么一段,解释了具体是如何去实现"Permutation"的
❝we 「keep the original sequence order」 , use the 「positional encodings」corresponding to the original sequence, and rely on a 「proper attention mask」 in Transformers to achieve permutation of the factorization order.
❞
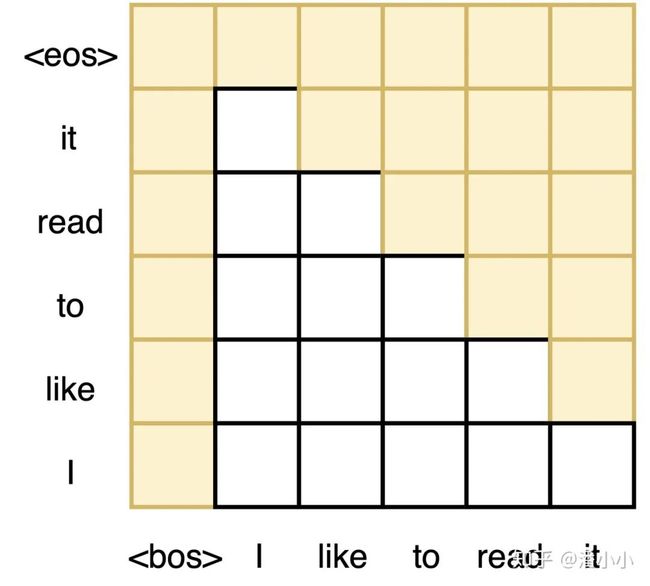
举例来详细解释一下,如下的3张图分别对应了不同的permutation,前2张图是同样目标序列输出对应的不同permutation顺序的输入,第3张图(从右向左)和前两张(从左向右)的目标序列不同(注意第3张图的解码实际顺序是it-read-to-like-,不是图中画的从下到上的顺序)。同理我们也可以得出"like-to-read-it-I"->"I-like-to-read-it"等permutation的mask。

作者也提供了一张图来解释这个机制:下图都是同一序列不同因式分解顺序,在解码 时的示意图。

「XLNet的优化目标函数」
sequence 「x」 的长度为
所有permutation的集合是
3.2. Target-aware Representations
「【问题】」 预测乱序中第t个token时,模型并不知道乱序中第t个对应的是原序列中的第几个。
回顾一下XLNet的优化目标函数中的 ,这个部分描述的是在解码permutated sequence中第t个位置的token时的概率
,其中 代表 经过 「按照permutation进行mask」(上一节有讲怎么mask)之后的Transformer输出的hidden representation。
我们注意到 和 的位置(也就是 )没有关系。不管 是1到T中(总长度为T)的哪个, 都完全一样。
「【解决方法】Target-aware Representations」
既然模型不知道将要预测的token在原序列中的位置,那么我可不可以告诉它呢?答案是可以的,这就是Target-aware Representations。具体的做法就是在预测 的时候同时将 作为输入传递给模型。
那么这时候的 就变成了
其中 在 的基础上,加上了关于position 的信息
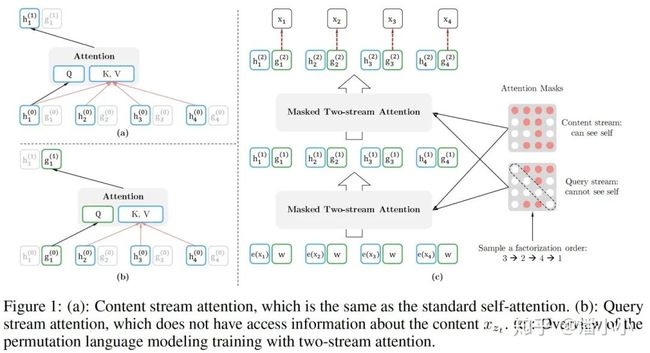
3.3. 双流自注意力机制(Two-stream Self-attention)
❝该机制的提出是为了实现上文所述的Target-aware Representations
❞
在考虑到使用上述Target-aware Representations来整个序列的解码过程时,发现了互相矛盾的两点:
预测 时,
预测 时, 应该同时使用position 和content
作者的解决思路是提出一种“双流机制”,也就是
Query Representation 只看得到之前的token+position,当前的position,但是看不到当前的token
Content Representation 可以看到之前的token+position,当前的token+position
Query Representations和Content Representations的更新过程如下:
「初始化」
Query Stream初始化为随机初始化:
Content Stream初始化即相应的Word Embedding:
「更新的公式」
如果self-attention有M层,对第m层
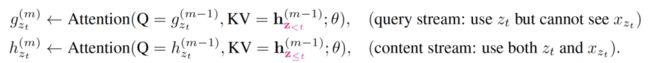
在finetune的时候,因为没有了permutation,也就不需要模型去预测 ,因此此时只需要使用content stream就可以了。
3.4. 部分打乱
一个长度为 的序列有 中permutation,这会导致训练过程中收敛非常的慢,于是我们采取折中的做法:只对序列的末尾几个token进行打乱,而对前面的部分保留原序列顺序。
![]()
往期精彩回顾
适合初学者入门人工智能的路线及资料下载机器学习及深度学习笔记等资料打印机器学习在线手册深度学习笔记专辑《统计学习方法》的代码复现专辑
AI基础下载机器学习的数学基础专辑获取一折本站知识星球优惠券,复制链接直接打开:https://t.zsxq.com/662nyZF本站qq群1003271085。加入微信群请扫码进群(如果是博士或者准备读博士请说明):