机器学习:系统设计与实现 分布式训练
机器学习系统:设计与实现 分布式训练
转自:https://openmlsys.github.io/chapter_distributed_training/index.html
随着机器学习的进一步发展,科学家们设计出更大型,更多功能的机器学习模型(例如说,GPT-3)。这种模型含有大量参数,需要复杂的计算以及处理海量的数据。单个机器上有限的资源无法满足训练大型机器学习模型的需求。因此,我们需要设计分布式训练系统,从而将一个机器学习模型任务拆分成多个子任务,并将子任务分发给多个计算节点,解决资源瓶颈。
在本章节中,我们会引入分布式机器学习系统的相关概念,设计挑战,系统实现和实例研究。我们会首先讨论分布式训练系统的定义,设计动机和好处。进一步,我们会讨论常见的分布式训练方法:数据并行,模型并行和流水线并行。在实际中,这些分布式训练方法会被参数服务器(Parameter Servers),或者是集合通信库(Collective Communication Libraries)实现。不同的系统实现具有各自的优势和劣势。我们会用大型预训练模型和大型深度学习推荐系统作为实例来探讨不同系统实现的利与弊。
本章的学习目标包括:
- 掌握分布式训练相关系统组件的定义,设计动机和好处
- 掌握常见的分布式训练方法:数据并行,模型并行和流水线并行
- 掌握常见的分布式训练框架实现:参数服务器和集合通信
- 理解常见分布式训练的实例,和采用不同实现方法的利弊。
1 系统概述
1.1 设计动机
接下来,我们详细讨论分布式训练系统的设计动机。
1.1.1 算力不足
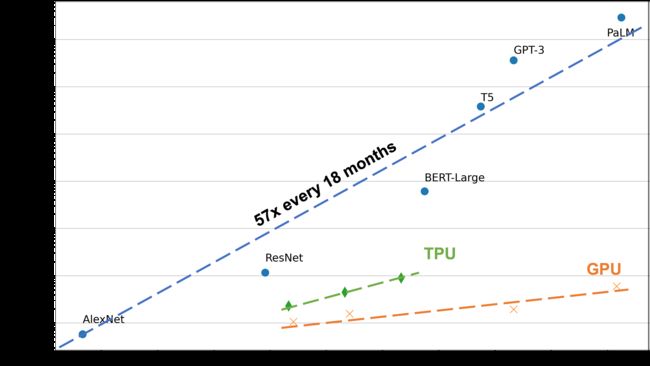
单处理器的算力不足是促使人们设计分布式训练系统的一个主要原因。一个处理器的算力可以用每秒钟浮点数操作(Floating Point Operations Per Second,FLOPS)来衡量。如图11.1.1所示,根据摩尔定律(Moore’s Law),中央处理器的算力每18个月增长2倍。虽然计算加速卡,如GPU和Tensor Processing Unit(TPU),针对机器学习计算(如矩阵相乘)提供了大量的算力。这些加速卡的发展最终也受限于摩尔定律,增长速度也停留在每18个月2倍。而与此同时,机器学习模型正在快速发展。短短数年,我们从仅能识别有限物体的AlexNet模型,一路发展到在复杂任务中打败人类的AlphaStar。这期间,模型对于算力需求每18个月增长了35倍。解决处理器性能和算力需求之间的鸿沟的关键就在于利用分布式计算。通过大型数据中心和云计算设施,我们可以快速获取大量的处理器。通过分布式训练系统有效管理这些处理器,我们可以实现算力的快速增长,从而持续满足模型的需求。
1.1.2 训练内存不足
在训练机器学习模型的过程中,训练系统需要在内存中存储大量数据。这些数据包括:模型参数(Parameters)以及训练和更新这些参数所产生的中间数据,如特征图(Feature Map)和梯度(Gradients)。假设一个深度神经网络模型具有10亿的参数,所有特征图共有20亿参数,每个参数都由一个32位浮点数表达,而更新这些参数至少还需要产生与特征图和参数等量的梯度。由于一个32位浮点数需要4个字节(Byte)的内存来存储,那么训练这个10亿规模的模型就需要至少24GB( 24 × 1 0 9 24×10^9 24×109 Byte)的内存。现在,随着大型预训练模型的崛起,一个深度神经网络(如GPT-3)会拥有超过千亿的参数。假设我们依然使用32位浮点数来存储参数,激活值和梯度,那么训练这个模型就至少需要1.2TB的内存。而如今的训练加速卡(如NVIDIA A100)仅能提供最高80GB的内存。单卡内存空间的增长受到硬件规格,散热和成本等诸多因素,难以进一步快速增长。因此,我们需要分布式训练系统来同时使用数百个训练加速卡,从而为千亿级别的模型提供所需的TB级别的内存。
1.2 分布式训练架构
受限于单节点的有限算力,内存和存储资源,人们把关注投向了日益成熟的云计算数据中心。一个数据中心管理着数十万个计算服务器。随着数据中心的全球部署,人们可以很方便地获得数百个服务器。这些服务器可以通过分布式训练系统来协调和管理,解决训练大型机器学习模型过程遇到的算力,内存和存储不足,从而完成训练过程的加速。
在设计分布式训练系统的过程中,我们需要找出有资源瓶颈的计算任务,根据计算任务的特点,将其拆分成多个子任务,然后将子任务分发给多个节点(可以是服务器,机器,或者是加速卡)并行完成。 图11.1.2描述了如何将单节点执行转换为分布式执行的一般过程。在机器学习系统中,一个计算任务往往会有一组数据(例如训练样本)或者任务(例如算子)作为输入,利用一个计算节点(例如GPU)生成一组输出(例如梯度)。假如单节点成为瓶颈,我们可以利用分布式计算进行加速。分布式执行一般具有三个步骤:第一步,我们需要将输入进行切分。第二步,每个输入部分会分发给不同的计算节点,实现并行计算。第三步,每个计算节点的输出,进一步合并,最终得到和单节点等价的计算结果。这种切分-并行-合并的模式,本质上实现了分而治之算法(Divide-and-Conquer Algorithm)的设计思想:由于每个计算节点只需要负责更小的子任务,因此其可以更快速的完成计算,最终形成对整个计算过程的加速。
1.3 用户益处
通过使用分布式训练系统,我们往往可以获得以下几个关键好处:
- 提升系统性能:使用分布式训练,往往可以带来训练性能的巨大提升。一个分布式训练系统往往用以下这个指标来衡量性能:到达目标精度所需的时间(time-to-accuracy)。这个指标由两个参数决定:一个数据周期所需的完成时间,以及一个数据周期模型所提升的精度。通过持续增加并行处理节点,我们可以将数据周期的完成时间不断变短,最终显著减少到达目标精度所需的时间。
- 经济性(Economy):使用分布式训练,我们也可以进一步减少训练及其模型所需的成本。受限于单节点散热的上限,单节点的算力越高,其所需的散热硬件成本也更高。因此,在提供同等的算力的条件下,组合多个计算节点是一个更加经济高效的方式。这促使云服务商(如亚马逊和微软等)需要更加注重给用户提供成本高效的分布式机器学习系统。
- 抵御硬件故障:分布式训练系统同时能有效提升抵御硬件故障的能力。机器学习训练集群往往由商用硬件(Commodity Hardware)组成,这类硬件(例如说,磁盘和网卡)运行一定周期就会产生故障。而仅使用单个硬件进行训练的话,那么一个硬件的故障就会造成整个训练的任务的失败。通过将这个训练任务由多个硬件共同完成,即使一个硬件故障了,我们也可以通过将这个硬件上相应的计算子任务转移给其余硬件,继续完成训练,从而避免训练任务的失败。
2 分布式训练方法
我们会讨论分布式训练系统实现的常用并行方法。我们首先给出并行方法的设计目标以及分类。然后,我们会详细描述各个并行方法。
2.1 概述
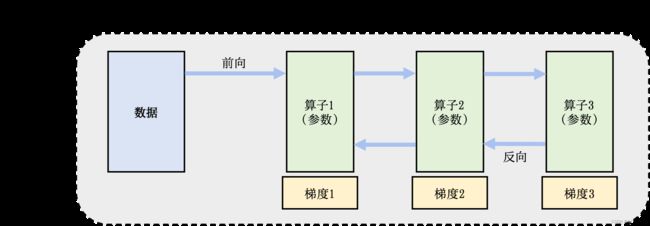
分布式训练系统的设计目标是:将单节点训练系统转化成等价的并行训练系统,从而在不影响模型精度的条件下完成训练过程的加速。一个单节点训练系统往往如 图11.2.1 所示。一个训练过程会由多个数据小批次(mini-batch)完成。在图中,一个数据小批次被标示为数据。训练系统会利用数据小批次来生成梯度,提升模型精度。这个过程由一个训练程序实现。在实际中,这个程序往往实现了一个多层神经网络的执行过程。该神经网络的执行由一个计算图(Computational Graph)表达。这个图有多个相互连接的算子(Operator),每个算子会拥有计算参数。每个算子往往会实现一个神经网络层(Neural Network Layer),而参数则代表了这个层在训练中所更新的的权重(Weights)。
为了更新参数,计算图的执行会分为前向传播和反向传播两个阶段。前向传播的第一步会将数据读入第一个算子,该算子会根据当前的参数,计算出传播给下一个算子的数据。算子依次重复这个前向传播的过程(算子1 -> 算子2 -> 算子3),直到最后一个算子结束。最后的算子随之马上开始反向传播。反向传播中,每个算子依次计算出梯度(梯度3 -> 梯度2 -> 梯度1),并利用梯度更新本地的参数。反向传播最终在第一个算子结束。反向传播的结束也标志本次数据小批次的结束,系统随之读取下一个小批次,继续更新模型。
| 单数据 | 多数据 | |
|---|---|---|
| 单程序 | 单程序单数据:单点执行 | 单程序多数据:数据并行 |
| 多程序 | 多程序单数据:模型并行 | 多程序多数据:混合并行 |
给定一个单节点训练系统,人们会对数据和程序分区(Partition),从而完成并行加速。 图11.2.1总结了不同的切分方法。单节点训练系统可以被归类于单程序单数据模式。而假如用户希望使用更多的设备来实现并行计算,他们首先可以选择对数据进行分区,并将同一个程序复制到多个设备上并行执行。这种方式是单程序多数据模式,常被称为数据并行(Data Parallelism)。另一种并行方式是对程序进行分区:程序的算子会被分发给多个设备按照依次完成。这种模式是多程序单数据模式,常被称为模型并行(Model Parallelism)。当训练超大型智能模型时,开发人们往往要同时对数据和程序进行切分,从而实现最高程度的并行。这种模式是多程序多数据模式,常被称为混合并行(Hybrid Parallelism)。
接下来,我们详细讲解各种并行方法的执行过程。
2.2 数据并行
数据并行往往可以解决单节点的算力不足。这种并行方式在人工智能框架中最为常见,具体实现包括:TensorFlow DistributedStrategy,PyTorch Distributed,Horovod DistributedOptimizer 等。在一个数据并行系统中,假设用户给定一个训练批大小 N N N,并且希望使用M个并行设备来加速训练。那么,该训练批大小会被分为 M M M 个分区,每个设备会分配到 N / M N/M N/M 个训练样本。这些设备共享一个训练程序的副本,在不同数据分区上独立执行,计算梯度。不同的设备(假设设备编号为i)会根据本地的训练样本估计出梯度 G i G_i Gi。为了确保训练程序参数的一致性,本地梯度 G i G_i Gi 需要聚合,计算出平均梯度 ( ∑ i = 1 N G i ) / N (\sum_{i=1}^NG_i)/N (∑i=1NGi)/N。最终,训练程序利用平均梯度修正模型参数,完成小批量的训练。
图11.2.2 展示了2个设备构成的数据并行例子。假设用户给定的批大小(Batch Size)是64,那么每个设备会分配到32个训练样本,并且具有相同的神经网络参数(程序副本)。本地的训练样本会依次通过这个程序副本中的算子,完成前向传播和反向传播。在反向传播的过程中,程序副本会生成局部梯度。不同设备上对应的局部梯度(如设备1和设备2上各自的梯度1)会进行聚合,从而计算平均梯度。这个聚合的过程往往由集合通信库(Collective Communication)的 Allreduce 操作来完成。
2.3 模型并行
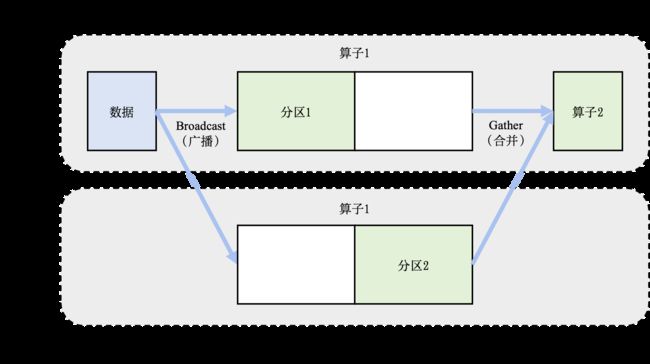
模型并行往往用于解决单节点的内存不足问题。一个常见的内存不足场景是模型中含有大型算子,例如说深度神经网络中需要计算大量分类的全连接层(Fully Connected Layer)。完成这种大型算子计算所需的内存可能超过单设备的内存容量。那么我们需要对这个大型算子进行切分。假设这个算子具有 P P P 个参数,而我们拥有 N N N 个设备,那么我们可以将 P P P 个参数平均分配给 N N N 个设备(每个设备分配 P / N P/N P/N 个参数),从而让每个设备负责更少的计算量,能够在内存容量的限制下完成前向传播和反向传播中所需的计算。这种切分方式是模型并行的应用,被称为算子内并行(Intra-operator Parallelism)。
图11.2.3给出了一个由2个设备实现的算子内并行的例子。在这个例子中,假设一个神经网络具有2个算子,算子1的计算(包含正向和反向传播)需要预留16G的内存,算子2的计算需要预留1G的内存。而本例中的设备最多可以提供10G的内存。为了完成这个神经网络的训练,我们需要对算子1实现并行。具体做法是,将算子1的参数平均分区,设备1和设备2各负责其中部分算子1的参数。由于设备1和设备2的参数不同,因此它们各自负责程序分区1和程序分区2。在训练这个神经网络的过程中,数据(小批量)会首先传给算子1。由于算子1的参数分别由2个设备负责,因此数据会被广播给这2个设备。不同设备根据本地的参数分区完成前向计算,生成的本地计算结果需要进一步合并(Combine),发送给下游的算子2。在反向传播中,算子2的数据会被广播给设备1和设备2,这些设备根据本地的算子1分区各自完成局部的反向计算。计算结果进一步合并传播回数据,最终完成反向传播。
另一种内存不足的场景是:模型的总内存需求超过了单设备的内存容量。在这种场景下,假如我们总共有 N N N 个算子和 M M M 个设备,我们可以将算子平摊给这 M M M 个设备,让每个设备仅需负责 N / M N/M N/M 个算子的前向和反向计算,降低设备的内存开销。这种并行方式是模型并行的另一种应用,被称为算子间并行(Inter-operator Parallelism)。
图11.2.4 给出了一个由2个设备实现的算子间并行的例子。在这个例子中,假设一个神经网络具有2个算子,算子1和算子2各自需要10G的内存完成计算,则模型总共需要20G的内存。而每个设备仅能提供10G内存。在这个例子中,用户可以把算子1放置在设备1上,算子2放置在设备2上。在前向传播中,算子1的输出会被发送(Send)给下游的设备2。设备2接收(Receive)来自上游的数据,完成算子2的前向计算。在反向传播中,设备2将算子2的反向计算结果发送给设备1。设备1完成算子1的反向计算,完成本次训练。
2.4 混合并行
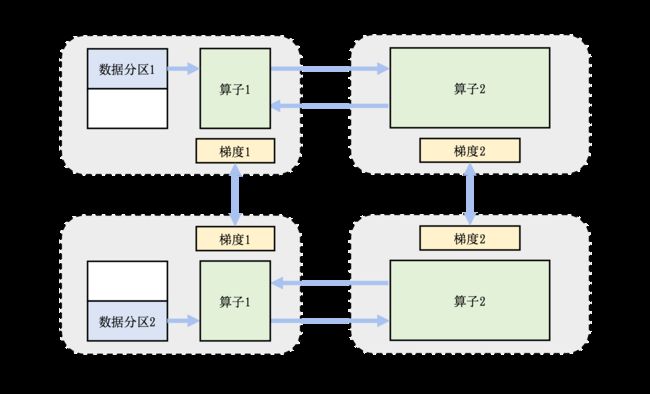
在训练大型人工智能模型中,我们往往会同时面对算力不足和内存不足。因此,我们需要混合使用数据并行和模型并行,这种方法被称为混合并行。 图11.2.5 提供了一个由4个设备实现的混合并行的例子。在这个例子中,我们首先实现算子间并行来解决训练程序内存开销过大的问题:该训练程序的算子1和算子2被分摊到了设备1和设备2上。进一步,我们通过数据并行来添加3和设备4,提升系统算力。为了达到这一点,我们对训练数据进行分区(数据分区1和数据分区2),并将模型(算子1和算子2)分配复制到设备3和设备4上生成可以并行执行的程序副本。在前向计算的过程中,设备1和设备3上的算子1副本同时开始,计算结果分别发送(Send)给设备2和设备4完成算子2副本的计算。在反向计算中,设备2和设备4同时开始计算梯度,本地梯度通过Allreduce进行平均。反向计算传递到设备1和设备3上的算子1副本结束。
3 流水线并行
在数据并行和模型并行以外,流水线并行是另一种常用的并行加速方法。流水线并行往往被应用在大型模型并行系统中。这种系统通过算子内并行和算子间并行解决单设备内存不足的问题。然而,当这类系统的运行中,计算图中的下游设备需要长期持续处于空闲状态,等待上游设备的计算完成,才可以开始计算,这极大降低了设备的平均使用率。这种现象被称为模型并行空洞(Model Parallelism Bubble)。
为了减少空洞,提升设备使用率,我们可以在模型并行系统中构建流水线。这种做法的核心想法是将一个数据小批量(Data Mini-batch)划分为多个微批量(Micro-batch)。假设一个数据小批量有 D D D 个训练数据,这个小批量可以被划分为 M M M 个微批量,那么微批量的大小就是 D / M D/M D/M。每个微批量相应进入训练系统,完成前向传播(Forwards propagation)和反向传播(Backwards propagation),计算出梯度。每个微批量对应的梯度将会缓存,等到全部微批量完成,缓存的梯度会被加和,算出平均梯度,更新模型参数。
图11.3.1 进一步给出了一个流水线并行的执行例子。在本例中,模型参数需要切分给4个设备存储。为了充分利用起来这4个设备,我们将小批量切分为2个微批量。当设备1完成第一个微批量的前向传播后(表示为 F 0 , 0 F_{0,0} F0,0)后,他会将中间结果发送给设备2,触发响应的前向传播任务(表示为 F 1 , 0 F_{1,0} F1,0)。与此同时,设备1也可以开始第二个微批量的前向传播任务(表示为 F 0 , 1 F_{0,1} F0,1)。前向传播会在流水线的最后一个设备–设备3–完成。系统于是开始反向传播。设备4开始第1个微批量的反向传播任务(表示为 B 3 , 0 B_{3,0} B3,0)。该任务完成后的中间结果会被发送给设备3,触发响应的反向传播任务(表示为 B 2 , 0 B_{2,0} B2,0)。与此同时,设备4会缓存好对应第1个微批量的梯度,接下来开始第2个微批量计算(表示为 B 3 , 1 B_{3,1} B3,1)。当设备4完成了全部的反向传播计算后,他会将本地缓存的梯度进行相加,并且除以微批量数量,计算出平均梯度,该梯度用于更新模型参数。
流水线并行的关键因素是流水线泡沫(Bubble)。当设备完成前向传播后,必须等到全部反向传播开始,在此期间设备会处于空闲状态。在 图11.3.1 中,我们可以看到设备1在完成2个前向传播任务后,要等很多时间才能开始2个反向传播任务。这其中的等待时间即被称为泡沫。为了减少设备的等待时间,一种常见的做法是尽可能的增加微批量的数量,从而让反向传播尽可能早的开始。然而,使用非常小的微批量大小,可能会造成加速器无法被充分利用。因此最优的微批量大小是多种因素的折中。其中最核心的因素是流水线泡沫的大小和加速器的计算能力。
4 集合通信
作为并行计算中的一个重要概念,集合通信算子经常会被用来构建单程序流/多数据流编程环境(single program-multiple data, SPMD)中的许多交互模式。近年来,该领域无论是在对不同硬件架构的支持还是算法性能的发展上都成果颇丰,而因SPMD在大型深度学习系统中与数据并行的深厚联系,这些框架也在其中受益匪浅。因此,相比点对点 (Point-to-Point, p2p) 通信,我们有更大的兴趣去探讨如何高效地在数据中心(Data Centers)中实现这些集合通信范式。首先,我们会介绍一些集合通信中常见的算子,一个经典的利用All算法解决分布式训练系统中网络瓶颈的示例,探讨该算法在不同网络拓扑结构下的差异性以及一些重要指标(算法带宽,总线带宽)的计算方法,最后简略介绍现有机器学习系统对不同集合通信算法的支持。
4.1 常见算子
在分布式内存模型(Distributed Memory Model)中,一些常见的进程间数据交互模式由硬件支持和并行算法的内在性质而涌现。因此,主流的并行计算架构标准(例如MPI)和机器学习系统的底层集合通信库(例如gloo,NCCL)通常会支持数个经典的算子并针对其做优化,一般包括Broadcast,Reduce,AllGather,ReduceScatter 和 AllReduce。在一个基于 [Sanders2019-cq] 的简化理论模型下,可以对这些算子的特性进行简单的介绍并探讨具体的实现方法和计算开销。
4.1.1 基本定义
首先,假定一个简化后的分布式内存模型:存在p个随机存取存储器(Random Access Machines, RAM)作为基础的处理单元(Processing Element, PE),并由一个网络来连接所有的机器。每个处理单元有自己的独立内存,并且所有的处理单元间的通信都通过网络传输。同时,每个处理单元都知道自己的编号i,通常在1到p之间。 网络之间的通信在最底层的情况下均为点对点的全双工通信(full-duplex point-to-point communication):
- 每次通信有且仅有一个发送者(sender)和一个接收者(receiver)。
- 在某个特定时刻,每个处理单元仅能至多发送或接收一个信息。但是,在网络中可以同时传输多个信息。每个处理单元也可以在发送一个信息的同时接收一个信息。
- 传输一个长度为l的信息会花费a+bl的时间,其中a代表延迟(latency),即单位信息通过网络从一个处理单元出发到达另一个处理单元所需的时间;b代表传输延迟(transmission delay),即把单位信息从处理单元中放到网络通信单元所需的时间。前者的大小一般取决于两个处理单元间的物理距离(同一个机架,同一个数据中心,横跨全球等),而后者的大小一般取决于通信网络的带宽。在这个模型下,假定所有处理单元之间的a和b均为恒定值。
- 通信可以指定一个发送者或者一个接收者:由于每个存储单元都有相对应的编号,我们可以定义两个函数send(i,l) 和receive(i,l)。其中send函数会把信息l从当前的处理单元发送至编号为i的处理单元,而receive函数会从编号为i的处理单元接收信息l。在调用send函数时,处理单元必须同时调用receive来保证编号为i的处理单元收到了该信息。因此,也可以说send和receive 同步(synchronize)了发送者和接收者。
- 作为拓展,我们也可以定义上述函数的一个变种:i = send(m) 和 i = receive(m),即在传输信息时不规定发送者或接收者。这种情况下,网络中的任意一个处理单元都可以发送或接收该信息,而最终完成传输的处理单元的编号会作为函数的返回值。
- 虽然在现实生活中错误(fault)时常发生,但是在这个模型里,暂不考虑通信丢失(dropped message)和通信毁坏(corrupted message)的情况。
分布式内存模型中对于通信同步和传输的结合使得在这个理论模型下开发的代码更好维护。额外的,由于这个框架下提出的算法往往会产生一些很有规律的,包含了网络中所有处理单元的交互模式,通常会在最基础的点对点通信上维护一个算子库,用来归纳总结这些高效且更易于理解的算法,我们将其称为集合通信算子。
4.1.2 Broadcast
在SPMD中,最常见的一个交互模式经常是把一个位于处理单元i的信息发送到全部其他的节点,用于同步某种全局的变量或者参数。为此Broadcast算子可以定义为从编号为 i i i 的处理单元发送长度为 l l l 的信息给全部剩余的 p − 1 p−1 p−1 个处理单元。在这里,一种简单的方法是在一个循环中使用 p − 1 p−1 p−1 次send/receive来实现Broadcast,但这并不能很好地利用通信可并行化的特质(该算法只有 ( a + b l ) ( p − 1 ) (a+bl)(p−1) (a+bl)(p−1) 的线性时间复杂度)。为此,我们可以利用分治思想(divide-and-conquer)来对上述算法进行优化。假设所有的处理单元可以重新对编号进行排列,使得Broadcast的发送者为编号为 1 1 1 的处理单元。同时,为了简化计算过程,假设对于某个自然数 n n n, p = 2 n p=2^n p=2n。 现在,我们可以通过从1 向 p / 2 p/2 p/2 发送一次信息来把问题转化为两个大小为 p / 2 p/2 p/2 的子问题:编号为1的处理单元对1到 p / 2 − 1 p/2−1 p/2−1 的Broadcast,以及编号为 p / 2 p/2 p/2 的处理单元对 p / 2 p/2 p/2 到 p p p 的Broadcast。我们便可以通过在这两个子问题上进行递归来完成这个算法,并把临界条件定义为编号为i的处理单元在 [ i , i ] [i,i] [i,i] 这个区间里的Broadcast。此时,由于i本身已经拥有该信息,我们不需要做任何操作便可直接完成Broadcast。这个优化后的算法有 ( a + b l ) l o g p (a+bl)logp (a+bl)logp 时间复杂度,因为在算法的每一阶段 t t t,我们有 2 t 2^t 2t 个计算单元在并行运行Broadcast算子。同时,算法一定会在 l o g p logp logp 步之内结束。
4.1.3 Reduce
除了Broadcast,另一个常见的交互模式为程序试图概述在部分处理单元上得到的中间值。这时候,对于一个符合结合律(associative property)的算子 f f f,我们可以定义Reduce算子,即将所有处理单元上的某个值两两配对重复应用该算子,并把最终结果储存在编号为 i i i 的计算单元上。常见的应用于Reduce中的算子有加和,乘积,最大值,最小值和平均值等。一个简易的Reduce的优化实现同样可以用分治思想来实现,即把 1 1 1 到 p / 2 − 1 p/2−1 p/2−1 的Reduce结果存到编号为 1 1 1 的处理单元中,然后把 p / 2 p/2 p/2 到 p p p 的Reduce结果存到 p / 2 p/2 p/2 上。最后,我们可以把 p / 2 p/2 p/2 的结果发送至 1 1 1,执行 f f f,并把最后的结果存至 i i i。假设f的运行时间复杂度为常数并不改变其输出信息的长度 l l l,Reduce的时间复杂度仍然为 ( a + b l ) l o g p (a+bl)logp (a+bl)logp。
4.1.4 AllReduce
AllReduce算子为Reduce的一个变种,即将f的结果存至所有处理单元上。在这里,我们给出一个简化版的 AllReduce 实现方式,即首先把最终值通过Reduce存到编号为 1 1 1 的处理单元,再将该值通过Broadcast广播到所有的处理单元上。在两个子算子都使用上述的算法情况下,AllReduce的时间复杂度仍为 ( a + b l ) l o g p (a+bl)logp (a+bl)logp。
4.1.5 Gather
Gather算子尝试将每个处理单元上的信息全部聚合到编号为 i i i 的处理单元上,通常用于组装散落在每个处理单元上的独立信息。在聚合函数符合结合律的情况下,可以通过将其设为Reduce算子中的 f f f 来实现Gather算子。但是,在这种情况下,无论是基于链表还是数组的实现,在每一步的Reduce子问题中f的时间复杂度或输出长度 l l l 都发生了改变。因此,Gather并不具有先前Reduce或者Broadcast的时间复杂度,而是 a l o g p + ( p − 1 ) b l alogp+(p−1)bl alogp+(p−1)bl。这是因为在算法的每一阶段 t t t,我们传输的信息长度为 l 2 t l2^t l2t。
4.1.6 AllGather
相比起Gather,AllGather 算子会把聚合的结果存到所有的处理单元上。在这里,一个简单的做法是使用Gather和Broadcast把聚合结果先存到编号为1的处理单元中,再将其广播到剩余的处理单元上。这会产生一个 a l o g p + ( p − 1 ) b l + ( a + p l b ) l o g p alogp+(p−1)bl+(a+plb)logp alogp+(p−1)bl+(a+plb)logp 的时间复杂度,因为在Broadcast时如果忽略链表/数组实现所带来的额外空间开销,每次通信的长度为 p l pl pl 而不是 l l l 。简化后,我们得到了一个 a l o g p + p l b l o g p alogp+plblogp alogp+plblogp 的时间复杂度。在一个基于超立方体的算法下,我们可以将其进一步优化到和Gather一样的 a l o g p + ( p − 1 ) b l alogp+(p−1)bl alogp+(p−1)bl (:cite:Sanders2019-cq),然而由于篇幅问题便不再赘述。
4.1.7 Scatter
Scatter算子可以被视作Gather的逆运算:把一个存在于编号为 i i i 的处理单元上,长度为 p p p(信息长度为 p l pl pl )的链式数据结构L中的值分散到每个处理单元上,使得编号为i的处理单元会得到 L [ i ] L[i] L[i] 。我们可以通过模仿Gather算法来设计一个简易的Scatter实现:每一步的运算中,与其是聚集一半处理单元的结果,我们把现在的子链继续对半切分,并把前半段和后半段作为子问题进行递归。这时候,在算法的每一阶段 t t t,我们传输的信息长度为 l 2 ( m − t ) l2^{(m−t)} l2(m−t) ,其中 m m m 是算法总共运行的步骤,不会超过 l o g p logp logp (见Broadcast)。最终,Scatter算子的检疫实现和Gather一样都有 a l o g p + ( p − 1 ) b l alogp+(p−1)bl alogp+(p−1)bl 时间复杂度。在机器学习系统中,相比于链式数据结构,Scatter经常同时被用于可切分的数据结构,例如张量(tensor)在一个维度上的 p p p 等分等。
4.1.8 ReduceScatter
ReduceScatter算子可以视为Reduce 和 Scatter算子的组合体,即对于每个处理单元上分别拥有的一个链式/可切分数据结构,在通过f 概述后再重新分散到各个单元中。虽然我们已经知道了Reduce 和Scatter 各自的时间复杂度,但是在对ReduceScatter做时间复杂度分析时需要注意两部之间信息长度的变化:假设每个处理单元上的数据结构所需通信长度为 p l pl pl,第一阶段的Reduce算法需要 ( a + p l b ) l o g p (a+plb)logp (a+plb)logp 时间复杂度。参照Scatter的分析,第二阶段的算子则需要 a l o g p + ( p − 1 ) b l alogp+(p−1)bl alogp+(p−1)bl 时间复杂度。综合下来,ReduceScatter 需要 a l o g p + p l b l o g p alogp+plblogp alogp+plblogp 的时间复杂度,和AllGather相同。同时,运行ReduceScatter 和 AllGather的效果等同于运行一次AllReduce。
在SPMD中,通常还有一些额外的集合通信算子,如Prefix Sum,Barrier,All-to-All等,但由于篇幅限制以及与机器学习系统的有限联系,便不再赘述。最后,由于该模型下通信网络的拓扑结构较为简单,上文中呈现二叉树形的递归树也可以达到很好的实际运行速度。所有关于时间复杂度的分析也是基于这些相对简化的假设情况。后文中,我们将会用AllReduce举例介绍如何在更复杂的拓扑结构下设计不同的集合通信算子变种,并在时间复杂度之外去关注实际的通信量和运算时间。
4.2 在数据中心的梯度计算
接下来,我们将用一个示例来阐释集合通信在机器学习系统中发挥的重要作用。
图11.4.1 描述了一个典型的用于深度学习模型训练的数据中心。数据中心中的训练服务器一般会有多个设备。如需增加服务器,我们会将多个训练服务器放置在一个机柜(Rack)上,同时接入一个架顶交换机(Top of Rack Switch)将其连接。在现有机柜满载的情况下,可以通过在架顶交换机间增加骨干交换机(Spine Switch)来接入新的机柜。通过这种方式,可以在数据中心内不断增加服务器,从而为神经网络的训练提供海量的算力和内存。目前的商用数据中心可拥有近百万台服务器。
在数据中心中训练大型神经网络的首要挑战是如何高效计算大量的平均梯度。假设给定一个千亿级别参数的神经网络(比如OpenAI 发布的大型语言模型GPT-3 [gpt-3] 有将近1750亿参数),如果用32位浮点数来表达每一个参数,那么每一步训练中,一个数据并行模式下的模型副本(Model Replica)则需要生成700GB的本地梯度数据(即 175G × 4 bytes = 700GB)。假如有3个模型副本,那么至少需要传输1.4TB(即,700GB × (3−1))的本地梯度数据(因为对于 N N N 个副本,只需传送其中的 N − 1 N−1 N−1 个副本来完成计算)。当平均梯度计算完成后,需要进一步将其广播(Broadcast)到全部的模型副本(即1.4TB的数据)并更新其中的本地参数,从而确保模型副本不会偏离(Diverge)主模型中的参数。
当前的数据中心一般使用以太网(Ethernet)构建不同机柜之间的网络。主流的商用以太网链路带宽一般在10Gbps到25Gbps之间。利用以太网传输海量梯度会产生严重的传输延迟,从而降低模型训练的速度。新型深度学习训练集群(如英伟达的DGX系列机器)往往配置有更快的Inifiband。单个InfiniBand链路可以提供100Gbps或200Gbps的带宽。即使拥有这种高速网络,传输TB级别的本地梯度依然需要大量延迟(即使忽略网络延迟,1TB的数据在200Gbps的链路上传输也需要至少40秒)。
为了避免通过机间网络传输数据,现代深度学习服务器一般都会配备多个加速器(例如说,英伟达的DGX-3服务器会配备8个A100 GPU),而在一个服务器内的多个设备可以通过高速机内网络互联(如NVLink)。这种高速机内网络可以提供高达400GBps的带宽,从而让传输TB级别的数据成为可能。然而,受限于单个服务器的散热,成本和硬件等限制,通常无法在一个服务器内无限制的持续增加设备。因此,大型深度学习模型的训练仍需要多个服务器共同完成。在计算平均梯度时,服务器需要同时借助机间网络通信接口(以太网或InfiniBand)和机内通信接口(NVLink)。
4.3 基于AllReduce的梯度平均算法
我们将讨论如何利用AllReduce算子来实现数据中心中的高效梯度平均。首先,参照前文的分析,可以考虑一种简单的计算平均梯度的方法:在集群中分配一个设备来收集本地梯度,并在计算平均梯度后再将其广播到全部的设备。这种做法易于实现,但是引入了两个问题。首先,多台设备同时给该聚合设备发送数据时,聚合设备会因严重的带宽不足产生网络拥塞。其次,单台设备需要负担大量的梯度平均计算,而受限于单台设备上的有限算力,这种计算往往会受限于算力瓶颈。
为了解决上述问题,可以引入AllReduce算子的Reduce-Broadcast实现来优化算法,其设计思路是:通过让全部的节点参与到梯度的网络通信和平均计算中,将巨大的网络和算力开销均摊给全部节点。这种做法可以解决先前单个梯度聚合节点的问题。假设有 M M M 个设备,每个设备存有一个模型副本,该模型由 N N N 个参数/梯度构成。那么按照AllReduce算子的要求,需要先将全部的参数按照设备数量切分成 M M M 个分区(Partition),使得每个分区具有 N / M N/M N/M 个参数。我们首先给出这个算法的初始和终止状态。如图11.4.2 所示,该例子含有3个设备。在每个设备有一个模型副本的情况下,这个副本有3个参数。那么按照AllReduce的分区方法,参数会被划分成3个分区(3个设备),而每一个分区则有1个参数( N / M N/M N/M, N N N 代表3个参数, M M M 代表3个设备)。在这个例子中,假定设备1拥有参数2,4,6,设备2拥有参数1,2,3,设备3拥有参数4,8,12,那么在使用AllReduce算子进行计算过后,全部的设备都将拥有梯度相加后的结果7,14,21,其中分区1的结果7是由3个设备中分区1的初始结果相加而成(7 = 1 + 2 + 4)。为了计算平均梯度,每个设备只需要在最后将梯度之和除以设备数量即可(分区1的最终结果为7除以3)。
AllReduce算子会把梯度的计算拆分成 M − 1 M−1 M−1 个Reduce算子和 M − 1 M−1 M−1 个Broadcast算子(其中 M M M 是节点的数量)。其中,Reduce算子用于计算出梯度的和(Summation),Broadcast算子用于把梯度之和广播给全部的节点。为了说明这些算子的执行过程,可以参照图11.4.3 。AllReduce算子由Reduce算子开始,在第一个Reduce算子中,AllReduce算子会对全部节点进行配对(Pairing),让他们共同完成梯度相加的操作。在图11.4.3 的第一个Reduce算子中,设备1和设备2进行了配对共同对分区1的数据相加。其中,设备2把本地的梯度数据1发送给设备1,设备将接收到1和本地的分区1内的梯度数据:2进行相加,计算出中间(intermediate)梯度相加的结果:3。与此同时,设备1和设备3进行配对,共同完成对分区3的数据相加。而设备3和设备2进行配对,共同完成对于分区2的数据相加。
在上述Reduce的算子中,梯度的计算实现了以下几个特性:
- 网络优化: 全部设备都同时在接收和发送数据,利用起了每个设备的入口(Ingress)和出口(Egress)带宽。因此AllReduce过程中可利用的带宽是 M × B M\times B M×B,其中M是节点数量,B是节点带宽,从而让系统实现网络带宽上的可扩展性。
- 算力优化: 全部设备的处理器都参与了梯度相加的计算。因此AllReduce过程中可利用的处理器是 M × P M\times P M×P,其中M是节点数量, P P P 是处理器数量,从而让系统实现计算上的可扩展性。
- 负载均衡: 由于数据分区是平均划分的,因此每次设备分摊到的通讯和计算开销是相等的。
在接下来的Reduce算子中,AllReduce算法会对不同数据分区选择另外的配对方法。例如说,在图11.4.3 的第二个Reduce算子中,AllReduce算法会将:设备1和设备3进行配对,负责分区1的数据相加。将设备1和设备2进行配对,负责分区2。将设备2和设备3进行配对,负责分区3。在一个3个节点的AllReduce集群里,在2个Reduce算子完成后,我们就计算出了每个分区的数据相加结果(分区1的结果7此时在设备3上,分区2的结果14此时在设备1上,分区3的结果21此时在设备2上)。
接下来,AllReduce算法将进入Broadcast阶段。这一阶段的过程和Reduce算子类似,核心区别是节点进行配对后,他们不再进行数据相加,而是将Reduce的计算结果进行广播。在图11.4.3 中的第一个Broadcast算子中,设备1会将分区2的结果14直接写入设备3的分区2中。设备2会讲分区3的结果21直接写入设备1中。设备3会将分区1的结果直接写入设备2中。在一个3个节点的AllReduce集群中,我们会重复2次Broadcast算子来将每个分区的Reduce结果告知全部的节点。
4.4 带宽计算
在讨论集合通信算子的性能时,人们经常会使用一些数值化指标去量化不同的算法实现,其中一个重要概念为带宽(Bandwidth)。在文献(:cite:nvidia-nccl)中,通常有两种主流的对带宽的计算方法,分别为算法带宽(Algorithm Bandwidth)与总线带宽(Bus Bandwidth)。
4.4.1 算法带宽
虽然算法带宽的计算方法既简单又高效,但很难将其拓展至对于集合通信算子的带宽计算。这是因为,取决于具体算子和算法实现的不同,一个集合通信算子在执行过程中测得的算法带宽往往会远小于硬件本身的最高带宽。在实际运行相应的测试中,经常能观测到随着处理单元增加,算法带宽呈下降趋势。为了解决这一问题,NCCL提出了总线带宽这一概念,通过对于每个集合通信算子的分析来对测得的算法带宽乘以一个校正系数(correction factor),来减轻处理单元数量对于测量带宽的影响并给出一个更贴近实际硬件表现的带宽值。下面列出了一些常见算子的校正系数,以及背后的简略推导。
- AllReduce: 2 ( p − 1 ) / p 2(p−1)/p 2(p−1)/p 对于在处理单元 n 1 , n 2 … n p n_1,n_2\dots n_p n1,n2…np 上的值 v 1 , v 2 … v p v_1,v_2 \dots v_p v1,v2…vp 计算 v 1 ( o p ) v 2 … ( o p ) v p v_1(op)v_2\dots (op)v_p v1(op)v2…(op)vp(其中op为符合结合律的算子),再存回每个处理单元中。在不考虑实际实现算法和网络拓扑的情况下,这个操作理论上只需要 2 ( p − 1 ) 2(p−1) 2(p−1) 次数据传输,其中包含在每个处理单元上分开进行的 n − 1 n−1 n−1 次 op的运算,以及最后 n n n 次最终数据值的广播,再减去第一个处理单元的运算和最后一个处理单元的广播的影响。假设每个处理单元对于外界所有信息处理的带宽为 B B B,我们可以得出对于 S S S 个在不同处理单元上的数据运行AllReduce是能得到的最优情况下的运行时间: t = ( 2 S ( p − 1 ) ) / ( p B ) t=(2S(p−1))/(pB) t=(2S(p−1))/(pB),进行简化后可得 B = ( S / t ) ( 2 ( p − 1 ) / p ) = b ( 2 ( p − 1 ) / p ) B=(S/t)(2(p−1)/p)=b(2(p−1)/p) B=(S/t)(2(p−1)/p)=b(2(p−1)/p)。这里的 2 ( p − 1 ) / p 2(p−1)/p 2(p−1)/p 便是我们的校正系数。
- ReduceScatter: ( p − 1 ) / p (p−1)/p (p−1)/p 对于每个处理单元来说,可以把ReduceScatter理解为只执行AllReduce中的聚合部分。对此,我们只需要考虑上文分析中的 n − 1 n−1 n−1 次op的运算,整理后可得 B = ( S / t ) ( ( p − 1 ) / p ) = b ( ( p − 1 ) / p ) B=(S/t)((p−1)/p)=b((p−1)/p) B=(S/t)((p−1)/p)=b((p−1)/p)。
- AllGather: ( p − 1 ) / p (p−1)/p (p−1)/p 同理,对于每个处理单元来说,可以把AllGather理解为只执行AllReduce中的广播部分。我们同理可得 B = ( S / t ) ( ( p − 1 ) / p ) = b ( ( p − 1 ) / p ) B=(S/t)((p−1)/p)=b((p−1)/p) B=(S/t)((p−1)/p)=b((p−1)/p)。
- Broadcast:1 与AllReduce不同的是,Broadcast中所有数据需要从算子本身的发送者发出。即使在上文的分治情况下,我们也需要等待所有子问题运行结束才能确保Broadcast算子本身的正确性。因此,在计算带宽时瓶颈仍为发送者对于外界所有信息处理的带宽,所以 B = S / t B=S/t B=S/t,即校正系数为1。
- Reduce:1 同Broadcast,Reduce需要将所有数据送往算子的接收者,因此校正系数同样为1。
由于Gather和Scatter的带宽计算与实际聚合/分散时的数据结构相关性更高,故不给出特定的校正系数。
4.5 样例分析
针对不同的集群性质,现代机器学习系统往往会灵活应用不同集合通信算子的组合来最大化通信效率。这里,我们提供了两个具体的案例分析,分别为微软的ZeRO 以及 OpenAI 的 DALL—E。
4.5.1 ZeRO
ZeRO (:cite:rajbhandari2020zero)是微软提出的神经网络优化器,可用于训练千亿级参数的神经网络,也在实践中成功训练了当时世界上最大的语言模型(为高达170亿参数的transformer)。在训练这个级别的神经网络时主要遇到的问题是巨量参数对于加速器内存的占用,其中包括优化器本身的参数,反向传播时的梯度,以及模型参数本身。通过简易的计算不难得出,170亿参数的模型在32位浮点表示情况下会占用至少680GB的内存,远超于现在内存最高的深度学习加速器A100 (最高内存80GB)。于是,我们需要考虑如何高效的把模型切成数份存储在不同的加速器上,以及如何高效的通过使用集合通信算子来进行模型训练和推理。ZeRO对此提出了多个优化方法,这里例举了三个典型的例子: 1. 首先,可以发现在现代集群中,节点内部加速器的带宽往往比节点之间的带宽要大很多。这在某种程度上偏离了上文中的理论框架。为此,我们需要尽量减少节点间的通信,尽量保证大部分通信仅存在于节点内部的加速器之间。在观察模型切分时,不难看出模型本身前馈和反向传播时需要大量的在不同切片之间通信,相比下来不同模型拷贝之间的梯度聚合反而具有相对较少的通信量。针对这一特性,ZeRO选择了将单一模型的全部切片存储到同一节点内部,从而大大提高了训练效率。 2. 进一步地,假设模型中的参数在层的细粒度上呈线性,便可将其从前到后分别存储到不同加速其中。在前馈时,可以注意到某一层的计算仅依赖于其相邻层的参数。对此,与其是手动设计点到点通信,我们可以对所有包含模型参数的加速器进行一次AllGather计算,用来提取每一层之后一层的参数,以及计算该层本身的激活值。为了节约内存,我们在AllGather结束后立即丢弃除了该层以外其他层的参数。 3. 同理,在反向传播时我们只需要前一层的参数来计算本层的激活值和梯度,因此我们只需要再次使用AllGather来完成每个加速器上的梯度计算。同时,我们注意到在聚集梯度后,对于每个加速器我们仅需要在内存中的层数的梯度。对此,我们可以使用ReduceScatter算子来在平均后直接把相应的梯度存到编号为i的加速器上,而不是通常情况下的AllReduce。
4.5.2 DALL-E
DALL-E (:cite:ramesh2021zero)是OpenAI提出的一个基于文字的图片生成模型,模型同样拥有高达120亿参数。在训练时,除了运用到ZeRO所使用的AllGather + ReduceScatter 技巧,OpenAI团队在细节上做了进一步的优化,以达到更快的训练速度。这里,我们简略介绍以下和集合通信相关的两点: 1. 我们注意到,集合通信算子的运行速度和通信本身的长度正相关。在模型训练中,这代表了模型参数本身的大小。对此,DALL-E 选择用矩阵分解(matrix factorization)的方法先把高维张量调整为一个二维矩阵,通过分解后分开用集合通信算子进行传输,从而大大减少了通信量。 2. 另一个减少通信量的方法在于数据类型本身。一个显然的做法是使用16位的半精度浮点数,相比正常的32位参数表示可以节省近一倍的通信量。但是,在实践中发现低精度的数据类型会使得模型收敛不稳定,往往导致最终训练效果大打折扣。为此,OpenAI分析了DALL—E 的模型结构,并把其中的参数根据对数据类型精度的敏感性分为了多个类。其中对精度最敏感的一类照常使用32位浮点表示并只通过AllReduce来同步,而最不敏感的参数则照常通过矩阵分解进行压缩和传输。对于比较敏感的一类,例如Adam 优化其中的动能(moments)和方差(variance)参数,OpenAI 基于 IEEE 754 标准实现了两个全新的数据类型:1-6-9和0-6-10(其中第一表示正负所需的位数,第二表示指数所需的位数,第三表示有效数字所需的位数),在节省空间和保持收敛性能之间找到了一个平衡。
4.6 集合通信与深度学习系统
最后,集合通信已经被深度集成到了整个机器学习系统之中,以至于一些在库级别以上的开发者很难意识到系统在训练和推理时的一些步骤是由底层逻辑实现的。 一般来说,不同的机器学习系统对于集合通信一般提供了两个级别的抽象,分别是更与硬件耦合的,可以直接调用集合通信算子的库,和更偏向神经网络实现的,通过内部调用集合通信算子来实现分布式训练和推理的深度学习框架。作为算法工程师,通常会接触到后者的抽象(包括Horovod, KungFu, TensorFlow distributed等),而作为集群的维护者,往往需要深入了解前者的运行原理和具体的调试方法。以深度学习框架 PyTorch 举例,在torch.distributed 命名空间(namespace)下实现了一系列方便开发者使用的分布式模型训练和推理函数。在其内部,会根据实际运行的集群调用更底层的集合通信算子库,例如MPI,NCCL(前文中已有介绍,适用于GPU分布式训练),gloo(适用于CPU分布式训练)等。我们来具体对比PyTorch distributed 中对于AllReduce 的应用和 NCCL 的差异性:下面两段代码中,前者(:cite:li2022ddp)通过PyTorch自带的分布式数据并行(Distributed Data Parallel)方法完成了一次简易的深度学习模型计算,后者则通过gloo的Python 接口pygloo和Ray(:cite:moritz2018ray)完成了一个二维张量的AllReduce计算。
import os
import sys
import tempfile
import torch
import torch.distributed as dist
import torch.nn as nn
import torch.optim as optim
import torch.multiprocessing as mp
from torch.nn.parallel import DistributedDataParallel as DDP
def setup(rank, world_size):
os.environ['MASTER_ADDR'] = 'localhost'
os.environ['MASTER_PORT'] = '12355'
dist.init_process_group("gloo", rank=rank, world_size=world_size)
class ToyModel(nn.Module):
def __init__(self):
super(ToyModel, self).__init__()
self.net1 = nn.Linear(10, 10)
self.relu = nn.ReLU()
self.net2 = nn.Linear(10, 5)
def forward(self, x):
return self.net2(self.relu(self.net1(x)))
def demo_basic(rank, world_size):
setup(rank, world_size)
model = ToyModel().to(rank)
# 通过调用DDP将模型在每个处理器上完成初始化
ddp_model = DDP(model, device_ids=[rank])
loss_fn = nn.MSELoss()
optimizer = optim.SGD(ddp_model.parameters(), lr=0.001)
optimizer.zero_grad()
outputs = ddp_model(torch.randn(20, 10))
labels = torch.randn(20, 5).to(rank)
# 在反向传播时,框架内部会执行AllReduce算法
loss_fn(outputs, labels).backward()
optimizer.step()
def run_demo(demo_fn, world_size):
mp.spawn(demo_fn,
args=(world_size,),
nprocs=world_size,
join=True)
if __name__ == "__main__":
n_gpus = torch.cuda.device_count()
assert n_gpus >= 2, f"Requires at least 2 GPUs to run, but got {n_gpus}"
run_demo(demo_basic, n_gpus)
import os
import ray
import pygloo
import numpy as np
import multiprocessing
@ray.remote(num_cpus=1)
def test_allreduce(rank, world_size, fileStore_path):
context = pygloo.rendezvous.Context(rank, world_size)
attr = pygloo.transport.tcp.attr("localhost")
dev = pygloo.transport.tcp.CreateDevice(attr)
fileStore = pygloo.rendezvous.FileStore(fileStore_path)
store = pygloo.rendezvous.PrefixStore(str(world_size), fileStore)
context.connectFullMesh(store, dev)
sendbuf = np.array([[1,2,3],[1,2,3]], dtype=np.float32)
recvbuf = np.zeros_like(sendbuf, dtype=np.float32)
sendptr = sendbuf.ctypes.data
recvptr = recvbuf.ctypes.data
# 标明发送者和者并直接调用AllReduce
pygloo.allreduce(context, sendptr, recvptr,
sendbuf.size, pygloo.glooDataType_t.glooFloat32,
pygloo.ReduceOp.SUM, pygloo.allreduceAlgorithm.RING)
if __name__ == "__main__":
ray.init()
world_size = multiprocessing.cpu_count()
fileStore_path = f"{ray.worker._global_node.get_session_dir_path()}" + "/collective/gloo/rendezvous"
os.makedirs(fileStore_path)
ray.get([test_allreduce.remote(rank, world_size, fileStore_path) for rank in range(world_size)])
可以注意到,前者并没有显式的调用集合通信算子,而是通过DistributedDataParallel将分布式训练和正常训练之间的不同隐藏了起来。如果我们需要在不同集群上运行这段代码,只需要在setup 函数内相对的更改PyTorch使用的底层集合通信库即可。在backward函数被调用时,才会真正的使用AllReduce算法。相比下来,如果想要直接使用gloo,不仅需要使用一步一步的创建通信所需要的数据结构,同时也很难和现有的模型训练框架无缝连接。
5 参数服务器
接下来,我们介绍另一种常见的分布式训练系统实现:参数服务器。常见的深度学习框架以不同方式提供了参数服务器。TensorFlow和MindSpore原生提供了参数服务器的实现;PyTorch需要用户使用框架提供的Rpc接口自行实现;还有一些框架则需要用户使用第三方的参数服务器实现,例如PS-Lite。
5.1 计算与存储分离
利用参数服务器的其中一个核心需求是实现:计算和存储的分离。在训练模型中,计算可以被理解为计算更新模型参数所需要的计算(例如说,计算本地梯度和计算平均梯度),而存储可以被理解为将模型参数存储在内存设备中(例如说,主机内存,加速卡内存和SSD设备)。传统的神经网络训练中,计算往往是核心瓶颈,因此我们只需要配置有合适数量的带有加速卡的服务器,常被称为训练服务器(Training servers)。
随着机器学习的发展,新型的稀疏模型被开发出来。相比于传统的神经网络训练,稀疏模型的训练往往不需要大量昂贵的计算加速卡(GPU),而需要海量的内存来存储嵌入表(Embedding table)。例如说,一个大型深度学习推荐系统中,它们往往使用小型的深度神经网络(如Multi-layer Perception),训练这种神经网络只需要几个GPU即可。而另一方面,推荐系统中往往需要存储PB级别的嵌入表。嵌入表往往由推荐系统的用户特征(User feature)和产品特征(Item feature)构成。这些特征往往是大型向量(Vector)。现代推荐系统需要服务数亿的用户,推荐数以千万的商品。假设用户的特征是1MB,而系统需要服务10亿的用户,那么用户的嵌入表就会有1PB的大小。而这个大小远远超过了一个深度学习服务器所具有的内存。假如我们部署大量的昂贵的深度学习服务器来存储海量嵌入表,那么这些服务器上的加速卡的使用率将会极低,无法实现对于硬件的高效利用。
为了解决上述问题,人们往往会在稀疏模型集群中混合部署:训练服务器和参数服务器,从而实现对于计算需求和内存需求分别满足。 图11.5.1 描述了带有参数服务器的机器学习集群。这个集群中含有2个训练服务器和2个参数服务器,训练服务器一般是拥有加速卡的计算优化服务器(Compute-optimised server)。而参数服务器一般是内存优化服务器(Memory-optimised server),其的内存大小一般远远大于计算优化服务器。在一个稀疏模型中往往拥有神经网络参数和嵌入表参数。神经网络较小,其可以存储在训练服务器内存中。而嵌入表很大,因此需要存储在额外的参数服务器中。参数服务器一般会按照键-值对(Key-value pairs)的方式来存储参数。常用的键包括用户名(User ID),产品名(Item ID)或者是参数名(Parameter Key)。常用的值是以多维度向量(Multi-dimensional tensors)表达的模型参数。假如存在多个参数服务器,参数服务器会用数据分区函数(例如,哈希函数和区域划分)将健-值映射到不同参数服务器上。
为了完成对于模型的训练,在每一步训练中,训练服务器会根据当前的小批量训练数据,找到本批量中需要用到的参数。例如说,本小批量数据只会训练部分用户的特征,那么这些用户的特征才会需要。根据参数服务器的数据分区函数,训练服务器可以知道参数当前在哪个参数服务器上,它们因此会用参数的键(Key)向对应的参数服务器发起拉取请求(Pull request)。参数服务器响应,并返回对应的值(Value)。训练服务器将拉取的参数(往往是嵌入表)和本地内存中的模型参数(往往是神经网络)进行合并,从而对合并的模型进行训练,计算梯度。假如训练服务器实现了数据并行,那么训练服务器计算出的本地梯度需要利用Allreduce计算出平均梯度。对于训练服务器本地内存中的参数,训练服务器可以马上利用平均梯度进行修改。对于在参数服务器中存储的参数,训练服务器发起推送请求(Push request)将平均梯度发送到参数服务器,参数服务器更新本地存储的参数。
在以上的参数服务器架构中,机器学习集群拥有者可以灵活的根据梯度计算所需要算力配置合理数量的训练服务器。他们也可以根据参数的数量配置大部分的稀疏参数(Sparse parameters)在参数服务器中,仅留下小部分的密集参数(Dense parameters)在训练服务器中。密集参数和稀疏参数的核心区别是:稀疏参数在每一步训练不一定都会被用到,他们需要根据当前训练小批量来决定。而密集参数每一步训练都需要用到。因此为了避免频繁从参数服务器中拉取,密集参数往往会存储在训练服务器中。
5.2 数据副本
在参数服务器的实际部署中,人们往往需要解决数据热点问题。互联网数据往往符合幂律概率(Power-law distribution),这会导致部分稀疏参数在训练过程中被访问的次数会显著高于其他参数。例如说,热门商品的特征向量被训练服务器拉取的次数就会远远高于非热门商品。因此,存储了热门数据的参数服务器所承受的数据拉取和推送请求会远远高于其他参数服务器,因此形成数据热点,伤害了系统的可扩展性。
解决数据热点问题的关键是利用在没有副本的情况下,通用的做法是每隔一段时间将所有参数在外存中保存一份检查点(checkpoint)。当出现机器故障时,首先所有的训练必须停止,等待故障的机器恢复上线,然后从外存中重新加载检查点。这就会导致从上一次保存检查点到故障发生时的数据全部丢失。保存一次检查点的开销随模型大小而增加,训练大模型时通常每隔1-2小时保存一次。因此无副本的参数服务器如果发生故障,会丢失最多1-2小时的数据。
解决参数服务器故障和数据热点问题的常用技术是构建模型主从副本(Master-slave replication)。一份参数在多个机器上拥有副本,并指定其中一个副本作为主副本。训练服务器的所有更新操作都向主副本写入并同步至从副本上。如何取得共识确定哪一个副本是主副本是分布式系统领域一个经典问题,已经有了相当多的成熟的算法,例如Paxos和Raft。此外,主副本上的更新如何复制到从副本上也同样是分布式系统领域的经典共识问题。通常系统设计者需要在可用性(Availability)和一致性(Consistency)之间做出取舍。如果参数服务器副本间采用强一致性的复制协议(例如,链式副本(Chain replication))则可能导致训练服务器的推送请求失败,即参数服务器不可用。反之,如果参数服务器采用弱一致性的复制协议,则可能导致副本间存储的参数不一致。
5.3 掉队者问题
参数服务器的另一大核心作用是可以让用户方便解决掉队者问题。在之前的讨论中,在每一步训练结束后,训练服务器都需要计算平均梯度来对每一个模型副本进行更新,从而保证下一步训练开始前,全部模型副本的参数的一致性,这种对于参数一致性的确保一般被称为同步训练(Synchronous training)。同步训练一般会有助于训练系统达到更好的模型精度,但是当系统规模变大,我们往往会在系统中引入掉队者(Straggler)。掉队者出现的原因很多。常见的原因包括:掉队者设备可能和其他设备不在同一个机柜中,因此掉队者的通讯带宽显著小于其他设备。另外,掉队者设备也可能和其他进程共享本地的服务器计算和通讯资源,形成资源竞争,从而降低了性能。
掉队者对于基于Allreduce的同步训练系统的性能有显著影响,这是因为Allreduce让全部节点参与到平均梯度的计算和通讯中,而每个节点负责等量的数据。因此任何一个掉队者的出现,都会让整个Allreduce操作延迟完成。为了解决这个问题,人们也会使用参数服务器来计算平均梯度。一种常见的设计是:训练服务器训练出本地梯度后,会把本地梯度全部推送到参数服务器。参数服务器在等到一定数据训练服务器(例如说90%的训练服务器)的本地梯度后,就开始计算平均梯度。这样可以确保平均梯度的计算不会被落后者的出现延误。计算好的平均梯度马上推送给全部训练服务器,开始下一轮训练。
解决掉队者的另外一种常见做法是利用参数服务器实现异步训练(Asynchronous training)。在一个异步训练系统中,每个训练服务器在训练开始时,有相同的模型参数副本。在训练中,他们计算出本地梯度后会马上将本地梯度推送到参数服务器,参数服务器将推送的梯度立刻用于更新参数,并把更新好的参数马上推送回对应的训练服务器。在这个过程中,不同的训练服务器很可能会使用不同版本的模型参数进行本地梯度的计算,这种做法有可能会伤害模型的精度,但它同时让不同训练服务器可以按照各自的运算速度来推送和拉取参数,而无需等待同伴,因此避免了掉队者对于整个集群性能的影响。
6 总结
- 大型机器学习模型的出现带来了对于算力和内存需求的快速增长,催生了分布式训练系统的出现。
- 分布式训练系统的设计往往遵循”分而治之”的设计思路。
- 利用分布式训练系统,人们可以显著提升性能,经济性,并且帮助抵御硬件故障。
- 分布式训练系统可以通过数据并行增加设备来提升算力。
- 当单节点内存不足时,我们可以通过模型并行来解决单设备内存不足。模型并行有两种实现方式:算子内并行和算子间并行。
- 大型模型并行系统容易出现设备使用空洞,而这种空洞可以通过流水线并行解决。
- 分布式训练系统往往运行在商用数据中心之中,数据中心网络无法提供充足的网络带宽来传输大量训练中生成的梯度。
- 为了提供海量的带宽,机器学习集群拥有异构的网络:以太网,机内网络(NVLink)和InfiniBand。
- 为了解决单节点瓶颈,我们可以使用Allreduce来分摊梯度聚合过程中的计算和通讯开销。
- 参数服务器可以帮助机器学习集群实现计算-存储的分离,从而更好的支持大型稀疏模型。
- 参数服务器常用数据副本技术解决数据热点问题,同时它们也可以被用来解决同步训练系统中常见的掉队者问题。
7 扩展阅读
- 分布式机器学习系统:综述
- 利用集合通信支持并行训练的实践:Horovod
- AllReduce的工程实现细节:树形结构,环形结构,二维环面结构,以及CollNet算法
- 流水线并行的实践:gPipe
- 在大规模数据并行下的实践:Accurate, Large Minibatch SGD: Training ImageNet in 1 Hour
- 模型并行在超大模型上的实践:ZeRO
- 最后,在讨论集合通信时,经常可以看到一些关于底层通信接口的专业术语,例如以太网,Infiniband 等。这里给出一些常见术语的具体定义:
- 以太网(Ethernet)
- NVLink
- AWS Elastic Fabric Adapter (EFA)
- Infiniband
- RDMA
- RoCE
- IPoIB