《计算机视觉之三维重建》笔记6-多视几何

北邮鲁鹏老师的课程《计算机视觉之三维重建（深入浅出sfm和SLAM核心算法）》 笔记

6，多视几何

6.1，运动恢复结构问题

问题：$n$个点$X_j$在$m$张图像中对应点$x_{ij}=M_i{X}_j$，已知$x_{ij}$，求$M_i,X_j$
三种任务：

1. 欧式结构恢复：内参数$K_i$已知 （实际常用）
2. 仿射结构恢复：仿射相机，内外参数未知
3. 透视结构恢复：透视相机，内外参数未知

6.2，欧式结构

问题：$x_{ij},K_i\Rightarrow X_j,R_i,T_i$
考虑两视图的情形，求解算法：

1. 归一化八点法求解基础矩阵$F$
2. 求解本质矩阵$E=K_2^{T}F{K}_1$
3. 分解本质矩阵$E\to R、T$
4. 三角化得到$X_{ij}$

本质矩阵分解：

定义：
$W=\left[\begin{array}{ccc}0& -1& 0\\ 1& 0& 0\\ 0& 0& 1\end{array}\right]Z=\left[\begin{array}{ccc}0& 1& 0\\ -1& 0& 0\\ 0& 0& 0\end{array}\right]$
则$Z=-diag(1,1,0)W=diag(1,1,0)W^T$
$[T_{\times }]=kUZ{U}^T$，$U$单位正交阵

证明1：
在垂直与向量$T$的平面上，取两个互相垂直的单位向量$u_1,u_2$，跟$T$的单位向量$u_3$一起构成单位正交矩阵$U=[u_1,u_2,u_3]$
则：$[T_{\times }]U=T\times [u_1,u_2,u_3]=[T\times u_1,T\times u_2,T\times u_3]=k[u_2,-u_1,0]=kUZ$
证明2：
反对称矩阵的性质，参考https://geek-docs.com/linear-algebra/matrix/fanduichen-matrix.html

不考虑符号尺度，$[T_{\times }]=Udiag(1,1,0)W{U}^T=Udiag(1,1,0)W^T{U}^T$
$E=[T_{\times }]R=Udiag(1,1,0)W{U}^{T}R=Udiag(1,1,0)W^T{U}^{T}R$
SVD分解：$E=Udiag(1,1,0)V^T$
可求得：
$R=det(UW{V}^T)UW{V}^T$或$R=det(U{W}^T{V}^T)U{W}^T{V}^T$
$T=\pm u_3$
得到四组解，选择重建的点的z轴为正的那组解。
欧式结构的恢复歧义：恢复的结构与真实场景存在相似变换

6.3，仿射结构

投影（透视）：$M=\left[\begin{array}{ll}A& b\\ v& 1\end{array}\right]$
仿射（弱透视）：$M=\left[\begin{array}{ll}A& b\\ 0& 1\end{array}\right]$
$x^E=(m_1,m_2{)}^T=[Ab]X=A{X}^E+b$
问题：$x_{ij}\Rightarrow X_j,A_i,b_i$
求解：

1. 数据中心化
   数据的中心${\bar{x}}_i=\frac{1}{n}{\sum }_k{x}_{ik},\bar{X}=\frac{1}{n}{\sum }_i{X}_i$，将数据减去其中心${\hat{x}}_{ij}=x_{ij}-{\bar{x}}_i,{\hat{X}}_i=X_i-\bar{X}$,可得：${\hat{x}}_{ij}=A_i{\hat{X}}_j$
   写成矩阵形式：
   $$D=\left[\begin{array}{llcc}{\hat{x}}_{11}& {\hat{x}}_{12}& \cdots & {\hat{x}}_{1n}\\ {\hat{x}}_{21}& {\hat{x}}_{22}& \cdots & {\hat{x}}_{2n}\\ & & \ddots & \\ {\hat{x}}_{m1}& {\hat{x}}_{m2}& \cdots & {\hat{x}}_{mn}\end{array}\right]=\left[\begin{array}{c}{A}_1\\ A_2\\ ⋮\\ A_m\end{array}\right]\left[\begin{array}{cccc}{\hat{X}}_1& {\hat{X}}_2& \cdots & {\hat{X}}_n\end{array}\right]=MS$$
2. 矩阵分解
   对$D$进行奇异值分解，取不为0的前三个特征值（理论上只有三个特征值不为0），$D=U_3{W}_3{V}_3^T$，得$M=U_3,S=W_3{V}_3^T$，从而得到$A_i,X_j$。

仿射结构的恢复歧义：差一个仿射变换
$D=M^{\ast }{S}^{\ast }=MH\cdot H^{-1}S$

4，透视结构

相机模型：$x_{ij}=M_i{X}_j$
$x=MX=M{H}^{-1}HX=M^{\ast }{X}^{\ast }$相差一个H变换

代数方法

两视图：
$$\begin{gathered} x_{1j}=M_1{X}_j=K_1[I,0]X_j \\ {x}_{2j}=M_2{X}_j=K_2[R,T]X_j \end{gathered}$$

1. 求解$F$矩阵
2. 分解$F\to M_1,M_2$

令$M_1^{\ast }=M_1{H}^{-1}=[I,0],M_2^{\ast }=M_2{H}^{-1}=[A,b]$
$x^{\prime }=[Ab]X=A[I0]X+b=Ax+b$
$x^{\prime }\times b=Ax\times b$
$0=-x^{\prime T}(x^{\prime }\times b)=-x^{\prime T}(Ax\times b)=x^{\prime T}(b\times Ax)=x^{\prime T}[b_{\times }]Ax=x^{\prime T}Fx$
$F=[b_{\times }]A$
$F^{T}b=0$，得到$b$为$F^T$最小奇异值的右奇异向量（$b$为极点）
$A=-[b_{\times }]F$

3. 三角化

捆绑调整BA

因式分解：都可见重建点少
代数法：两两算，有累积误差
BA，最小化重投影误差:
$E(M,X)={\sum }_{i=1}^m{\sum }_{j=1}^{n}D(x_{ij},M_i{X}_j{)}^2$
实际用于sfm最后一步，用分解或代数法的解作为其初始解

补充

PnP

Perspective-n-Points，已知$K,X_j,x_j$，求相机位姿。

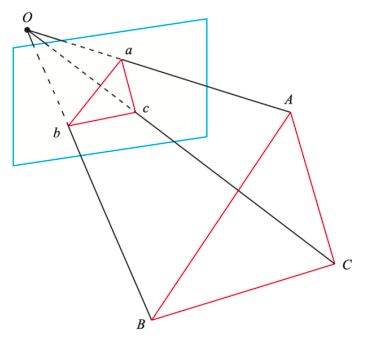
P3P:
已知相机内参数$K$，空间三个点$A,B,C$及其对应图像点$a,b,c\Rightarrow R,T$

求解：
在相机坐标系下：$p=KP$，所以图像点对应的相机坐标系下的三维坐标$P=K^{-1}p$
可得：$K^{-1}a=oa,K^{-1}b=ob,K^{-1}a=oc$（直线的方向，相差一个尺度）
从而可求得：$cos<oa,ob>,cos<oa,oc>,cos<ob,oc>$
求解方程：
$$\{\begin{array}{c}O{A}^2+O{B}^2-2OA\cdot OBcos<oa,ob>=A{B}^2\\ O{B}^2+O{C}^2-2OB\cdot OCcos<ob,oc>=B{C}^2\\ O{A}^2+O{C}^2-2OA\cdot OCcos<oa,oc>=A{C}^2\end{array}$$
得到四组$OA,OB,OC$的解，结合另一对点对应D来确定唯一解。
根据上面求得的方向和长度，可以确定$A,B,C$在相机坐标系下的坐标，结合其世界坐标，可求得$R,T$

RANSAC

RANdom SAmple Consensus

1. 随机均匀采样获取模型求解所需最小子集，个数为$s$；
2. 估计模型参数；
3. 计算剩余样本跟当前模型的一致性，统计内点数作为模型分；
4. 重复1-3步$N$次，输出得分最高的模型；

样本的外点率为$e$，$N$次采样中，至少有一次采样的点全部是内点的概率为$p$，则有：
$$(1-(1-e{)}^s{)}^N=1-p$$
所以，给定$p$，至少需要$N$次迭代：
$$N=\log (1-p)/\log (1-(1-e{)}^s)$$