SLAM算法 -LOAM框架分析(一)

算法简介

LOAM的整体思想就是将复杂的SLAM问题分为：1. 高频的运动估计(10HZ) 2. 低频的环境建图(1HZ)。
在运动估计中采用scan-to-scan方式，同时对点云进行了计算曲率，筛选线面特征,降低匹配数据量, 通过点到线和点到面构造误差函数，在求解变换关系前，通过匀速假设构造线性插值关系，对点云进行运动补偿后用非线性优化LM求解匹配;
在环境建图中采用map-to-map方式匹配，采用了PCA主成分思想提取线面特征，达到降维的目的,保证匹配精度的同时提升匹配效率。帧间匹配还有scan-to-map方式,主要差异体现在计算效率和匹配误差精度上。

添加对系统框图的关键流程理解：

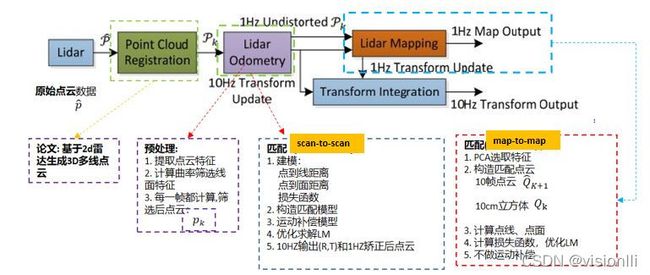
从个人角度看理解loam算法的精髓主要思考两点：
(1) 如何选择特征让匹配效率更高
(2) 匹配误差模型如何建立,更精确的描述运动过程

1 激光里程计(高频率)

1.1 计算曲率

我们知道曲线的曲率(curvature)指曲线上某个点的切线方向角对弧长的转动率,通过微分来定义,表明曲线偏离直线的程度。数学上表明曲线在某一点的弯曲程度的数值。曲率越大,表示曲线的弯曲程度越大,在点云中曲率越大的点集表示线,曲率越小的点表示面。LOAM在匹配前先对每一个点计算曲率, 曲率会用于下一步的筛选线和面特征。先看论文中定义的曲率公式：

问题的关键这个公式怎么来的了？如何理解？
这里需要提一下3D数据滤波 - laplacian平滑中的思想：
3D深度图滤波可以按照物理距离查找到相邻域的点集，用邻域点集的平均值代替滤波前点,实现平滑：

问题思路就在这里，假设我们不用邻域点集的平均值代替滤波前的点, 可以用一个权重w(即论文中的曲率c)描述滤波前的点和滤波后的点的接近程度(邻域点集平均值表示), 由于原论文和大多数博客只有结论，这里按照个人的理解给出公式的推导:

1.2 筛选特征

基于以上每个点的曲率计算公式，筛选特征点，按照c在不同范围的阈值，可以将点分为四类：
(1) 曲率特别大的点：charp
(2) 曲率大的点：less_sharp
(3) 曲率特别小的点:flat
(4) 曲率小的的：less_flat
最终选择以上的曲率特别大的点(charp)为边缘点(线),曲率特别小的点(flat)为平面点。

1.3 问题建模

1.3.1 损失函数

筛选完特征点后，可以对连续特征帧进行匹配,需要建立误差模型。LOAM中采用点到线的距离，和点到面的距离构造误差函数。
注意在下面讨论(1)和(2) ， 点到线和点到面中点的含义指的是K+1帧点经过变化后在K参考帧的变换点，即变换后的点到线和点到面。
(1) 点到线的距离
这里的点指第k+1帧经过变换后的点, 线指第k帧经过筛选后的点云中的特征线，距离计算即求d(P,Line)。计算距离有很多方式，论文使用叉乘来实现。在2d和3d中，直线L是由两个点P0和 P1确定，可以使用叉乘直接计算从任意一点P到直线L的距离。

(2) 点到面的距离

(3) 理论误差函数
问题变为求解：

即第k+1帧点云中的第i个点的变换点到参考点云的所有的点到线和点到面的距离的累加和为求解的问题模型, 加入旋转R和平移t。

可以写出第k+1帧原始点云第i点和变化后的点云(以上推导都是)之间关系：

Loss函数变为:

貌似只要用优化的方法求解，就可以得到最佳的结果。实际雷达的频率不够快,主要有几点：
(1) 激光点数据不是瞬时获取,同一帧点云不同位置的点时间戳不一样
(2)激光扫描时,本身伴随着机器人移动
因此,激光点云频率较低时，机器人的运动补偿不得不考虑进去。

1.3.2 运动补偿

运动补偿就是需要将一帧点云中的所有不同时间戳的位置点补偿到同一个时间戳，这个时间戳不一定要求是开始扫描点的时间，可以介于任意之间任意一个时刻。补偿的方法是需要知道每个时间戳对应的点的位置，假设知道起始扫描点的姿态，相对于起始点的姿态该怎么计算了，有不同的方法：
(1) 高频率里程计校准

如果里程计中融合IMU可以对旋转角度进行高精度补偿。通过硬件传感器可以实现将一帧点云中不同时刻的位置都变换到起始时刻，不同点的时间戳为同一个时间戳。假如没有这些传感器该怎么解决了？怎么获取Delt(odom)？

(2) 匀速模型假设
匀速模型假设就是假设K-1时刻到K时刻的里程计变化量(帧间匹配)与K到K+1时刻的里程计变化量相等,同时假设K+1帧也是匀速运动,采用线性插值可以估计出每个点相对起始时刻的位姿。

采用线性插值后得到：

(3) 修正误差函数
没有考虑补偿的第k+1帧原始点云第i点和变化后的点云之间关系，经过运动补偿后为：

整理得到优化损失函数：

注意：
矩阵R是满足罗德里格斯变换的旋转矩阵 loam-velodyne采用欧拉角计算的，A-LOAM采用四元数计算。

最终的loss函数满足：

1.4 优化求解

论文采用LM算法进行优化求解，具体算法可以看优化课程。只关心迭代过程：

其中，雅可比矩阵J, 具体如何解决雅可比矩阵：

多元函数在某一点的梯度是一个非常特殊的向量，其由多元函数对每个变量的偏导数组成（这即是为什么求梯度的时候需要对各个变量求偏导的原因），其方向为函数在该点增加最快的方向，大小为函数在该点的最大变化率。向量求导

1.5 定位输出

以上不断的匹配计算的是相邻两点云之间的平移变换，即激光里程计，是在雷达坐标系L下,需要转化到全局地图坐标系W下：

2 环境建图(低频率)

2.1 问题模型

高频里程计的不断的输出经过补偿后校准的点云帧序列,以及其对应的激光在全局坐标系下的姿态，但是以上是基于scan-to-scan的匹配方式，效率虽然提高了，但是精度不高。可以思考是否基于以上不精确的初值再做一次匹配, 参考帧选择基于初值附近的局部点云地图，待匹配帧采用基于初值后的一定梳理的被校准过的连续帧，论文中取10帧。

问题的模型变为：给定初值，计算两团(每团包含不同数量点云)的之间变换，并求解全局坐标。

由上图知道OA已知是由激光里程计输出的不精确姿态，要输出OB，则需要先基于两团点云(每团包含不同数量帧点云）计算AB，这里也是属于帧间匹配问题， 那么计算两团点云如何计算了？
(1) 点云团的数量量大，需要降低数据量，即采用特征手段或者其他方法匹配，降低数据量。
(2) 与激光里程计(高频率)中计算曲率筛选特征不同，这里采用计算点相邻点集合的协方差，判断边缘点和平面点
(3) 筛选了边缘点和平面点之后的过程都是一样，包括问题建模和LM优化。
因此，我们只需深入讨论协方差如何判断边缘点(线特征)和面特征？这里包含了点云的哪些基础知识点了？
主要思想是PCA分析3D点云的几何形状参数，如下介绍:

2.2 PCA特征

(1) 基本原理
可以参考博客PCA：详细解释主成分分析 借用其中一句解释PCA思想：

最大方差理论:方差越大，信息量就越大。协方差矩阵的每一个特征向量就是一个投影面，每一个特征向量所对应的特征值就是原始特征投影到这个投影面之后的方差。由于投影过去之后，我们要尽可能保证信息不丢失，所以要选择具有较大方差的投影面对原始特征进行投影，也就是选择具有较大特征值的特征向量。然后将原始特征投影在这些特征向量上，投影后的值就是新的特征值。每一个投影面生成一个新的特征，k个投影面就生成k个新特

PCA是最常用的线性降维方法，它的目标是通过某种线性投影，将高维的数据映射到低维的空间中，并期望在所投影的维度上数据的信息量最大（方差最大），以此使用较少的数据维度，同时保留住较多的原数据点的特性。

(2) 计算方法
PCA的核心思想是矩阵的特征值分解。将一团点云看成时3D的"椭球体", 可以用PCA主成分分析椭球体三个轴的方向(主方向),三个轴相互垂直。
主要计算方法流程如下：

(3) 分析结论
(1) 特征λi值代表点云在该方向上(基座标)的投影后的方差大小，方差代表点的离散程度
(2) 特征值越大，方差越大，点越分散到此特征值对应的方向上 ,反之越小方差越越小，点越集中，越远离该方向
(3) 可以知道线特征都分散到一个基座标，面特征都分散到两个基座标
基于以上可以方法可以筛选出点云中的边缘点(线)和平面点，如下图所示：

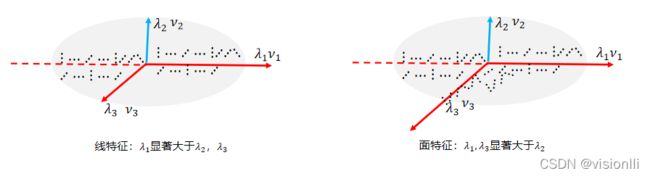
（4）直线和平面方程

算出直线和平面的法向量，就可以继续按照点到线和点到面，计算损失函数。其他优化过程与高频激光里程计部分一样。

参考文献

[1] https://zhuanlan.zhihu.com/p/111388877
[2] http://www.everyinch.net/index.php/computergeometry2/
[3] https://www.zhihu.com/question/58312854
[4] https://blog.csdn.net/lanyuelvyun/article/details/82384179