CVPR 2022 | NeW CRFs: Neural Window Fully-connected CRFs for Monocular Depth Estimation
CVPR 2022 | NewCRF:使用Attention模拟了CRF
- 论文:https://arxiv.org/abs/2203.01502
- 代码:https://weihaosky.github.io/newcrfs/
核心内容
 |
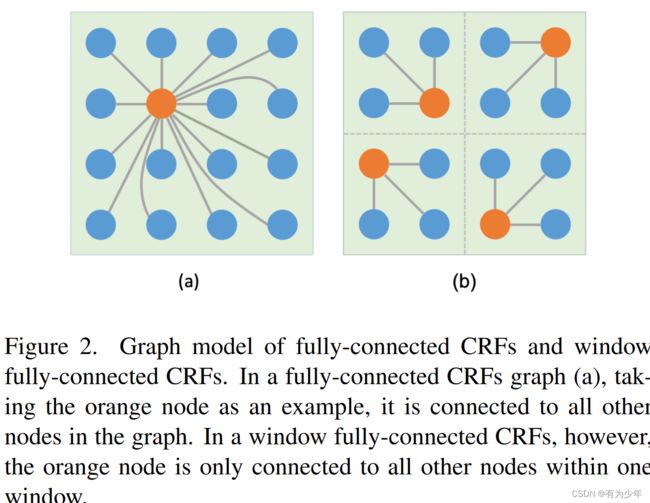 |
这篇文章将全局全连接CRF使用Attention进行了改造,并使用了基于窗偏移的计算过程实现了更低的计算量。提出的结构被用于单目深度估计任务模型的构建中。
背后动机
随着深度估计的发展,这一领域实际上逐渐变成了在缺少其他引导帮助的情况下的一种困难的拟合问题。
传统单目深度估计的算法中有一些会利用马尔科夫随机场MRF或者条件随机场CRF来优化深度预测。他们利用一些观测线索,例如纹理和位置信息,搭配最后的预测来一起构建能量函数,之后优化这个能量函数从而获得深度估计。
由于其引导深度估计的有效性,所以这也被用在了后来的一些深度方法中。然而,受限于全连接CRF的高昂计算量,大多数方法会直接使用局部版本,也因此放弃了全连接CRF本身捕获全局关系的能力。
为此,基于窗口偏移的策略构架了全连接CRF的能量函数。从而有效降低了计算复杂度还保证了全局关联。同时也通过集成来自全局平均池化层的全局特征从而引入全局信息。
同时也利用了多头注意力机制来计算CRF中成对隐函数,从而捕获更多样的关系形式。最终构建了一个新的neural CRFs模块。
这一neural windows FC-CRFs模块被用作U型深度估计模型中解码器中的基本构建单元。
现有方法
对于深度估计的研究早在深度学习出现之前就已经开始了。早期的方法往往局限于估计障碍物的一维距离或者是在一些已知且固定的目标中进行分析。
后来的工作Learning depth from single monocular images中认为局部特征不足以用来预测像素深度,并且整个图像的全局上下文需要被考虑在其中。因此他们使用判别训练(discriminatively-trained)的MRF来合并多尺度的局部和全局的图像特征,并且同时在独立的像素上的深度和不同像素上的深度关系上建模。以这种方式,他们从色彩、像素位置、障碍物、已知的目标尺寸、模糊、失焦等单目线索中获得良好的深度估计。
此后MRF和CRF就多被用于传统的单目深度估计中。然而,传统的方法对于准确估计高分辨率密集深度图而言,还是有些吃力。
在深度学习方法中,主要有两种类型的方法来学习从图像到深度图的映射。
- 第一种是直接从图像信息的聚合中,回归连续的深度图。
- 第二种则是尝试去离散深度空间,将深度估计转化为一个分类问题或者是顺序回归问题。
而其他的一些方法则尝试引入一些辅助信息来辅助深度网络的训练,例如稀疏深度或者分割信息等等。
所有的这些方法都是在尝试通过图像特征直接回归深度图,这是一个困难的拟合问题。网络的结构也变得越来越复杂。
相较于这些方法,本文的方法则是通过构建更低复杂度的全连接CRF的能量函数来获得高质量的深度图。而且本文的方法将CRF模块与模型融合在一起,可以实现端到端训练。
提出的方法
Neural Window FC-CRFs
原始的FC-CRFs:
E ( x ) = ∑ i ψ u ( x i ) + ∑ i , j ψ p ( x i , x j ) ψ u ( x i ) = − l o g P ( x i ∣ I ) ψ p ( x i , x j ) = μ ( x i , x j ) f ( x i , x j ) g ( I i , I j ) , h ( p i , p j ) \begin{align} E(\mathbf{x}) & = \sum_i \psi_u(x_i) + \sum_{i,j} \psi_p(x_i, x_j) \\ \psi_u(x_i) &= -logP(x_i|I) \\ \psi_p(x_i, x_j) &= \mu(x_i, x_j) f(x_i, x_j) g(I_i, I_j), h(p_i, p_j) \end{align} E(x)ψu(xi)ψp(xi,xj)=i∑ψu(xi)+i,j∑ψp(xi,xj)=−logP(xi∣I)=μ(xi,xj)f(xi,xj)g(Ii,Ij),h(pi,pj)
- i , j i,j i,j用于索引图上的所有节点。
- ψ u \psi_u ψu为unary potential function。
- ψ p \psi_p ψp为pairwise potential function。
- μ ( x i , x j ) \mu(x_i, x_j) μ(xi,xj)在 i = j i=j i=j的时候为1,反之为0。即指示是否为同一个节点
- f ( x i , x j ) f(x_i, x_j) f(xi,xj)表示节点 i i i与 j j j的预测值的差异,一般为 ∣ ∣ x i − x j ∣ ∣ ||x_i - x_j|| ∣∣xi−xj∣∣。
- g ( I i , I j ) g(I_i, I_j) g(Ii,Ij)表示节点间的颜色的差异,一般为 exp ( − ∣ ∣ I i − I j ∣ ∣ 2 σ 2 ) \exp(-\frac{||I_i - I_j||}{2 \sigma^2}) exp(−2σ2∣∣Ii−Ij∣∣)。
- h ( p i , p j ) h(p_i, p_j) h(pi,pj)表示节点的位置的远近,一般为 exp ( − ∣ ∣ p i − p j ∣ ∣ 2 σ 2 ) \exp(-\frac{||p_i - p_j||}{2 \sigma^2}) exp(−2σ2∣∣pi−pj∣∣)。
在图模型中,CRF的能量函数通常由两项组成:
- 一项被称为unary potential function,其计算每个节点自身的表征。由预测器根据图像特征计算得到。在本文的算法中,直接通过一个独立的unary network计算得到。unary network是一个简单的卷积网络,但是我在代码https://github.com/aliyun/NeWCRFs/blob/master/newcrfs/networks/newcrf_layers.py中并未找到这一部分内容。
- 另一项则是pairwise potential function,这同时考虑当前节点与图中其他节点之间的关系。这一函数通常会考虑两个节点之间的色彩、位置信息,来执行一些启发式的惩罚(heuristic punishment),这将使得预测结果更加合理和符合逻辑,例如外观相似、距离相近的两个节点自然最终的预测应该更加一致,而反之则应该具有不同的预测。
- 这一函数的设计通常基于人工经验,很难表达高维信息并描述复杂的连接形式。本文使用神经网络来构建这一函数,所以表征能力也更强。
- 通过对该函数原始形式的意义拆解与转化,最终使用基于相对位置嵌入的注意力机制代替了这一函数的原始形式。QK的计算就是计算节点之间权重的过程,而位置信息则由位置嵌入来引入。所以转换后,对于第 i i i个位置上的这一项的形式为: ψ p i = softmax ( Q i ⋅ K ⊤ + P i ) ⋅ X ∈ R 1 × D \psi_{p_i} = \text{softmax}(Q_i \cdot K^\top + P_i) \cdot X \in \mathbb{R}^{1 \times D} ψpi=softmax(Qi⋅K⊤+Pi)⋅X∈R1×D,我个人理解的转化过程可以见下面的分析。
- 在面对更大范围的计算中,这项其会带来过高的计算成本。考虑到实际像素的深度估计中,通常并不由非常远的像素决定,所以只需要考虑某些距离范围内的像素就行。因此,这份工作提出了基于窗口的优化策略。将图像特征划分为多个不重叠的patch,在每个patch中计算FC-CRF。从而有效降低了计算复杂度。为了缓解窗口之间的孤立性,引入了窗口偏移的机制。通过对窗口偏移一半(Swin的形式)后再次计算能量函数。因此,每次都会顺序计算两次能量函数。
在由神经网络构成的能量函数之后,会接一个优化网络,包含两个全连接层来输出优化后的深度图。optimization network包含两个全连接层,在作者的代码中https://github.com/aliyun/NeWCRFs/blob/master/newcrfs/networks/newcrf_layers.py中似乎对应的是attention中的mlp结构。
另外需要注意的是,每个解码器stage的输出并不是直接就是优化后的深度图,而是一个独立的特征。作者论文中的表述的很有误导性。Then the energy function is fed into an optimization network composed of two fully-connected layers to output the optimized depth map X′.
pairwise potential function的转换过程
ψ p ( x i , x j ) = μ ( x i , x j ) f ( x i , x j ) g ( I i , I j ) , h ( p i , p j ) ⇒ μ ( x i , x j ) w ( F i , F j , p i , p j ) ∣ ∣ x i − x j ∣ ∣ ⇒ w s ( F i , F j , p i , p j ) x i + μ ( x i , x j ) w o ( F i , F j , p i , p j ) x j ⇒ ψ p i = ∑ j ψ p ( x i , x j ) ⇒ ∑ j [ w s ( F i , F j , p i , p j ) x i + μ ( x i , x j ) w o ( F i , F j , p i , p j ) x j ] ⇒ w s ′ ( F i , F j , p i , p j ) x i + ∑ j ≠ i w o ( F i , F j , p i , p j ) x j ⇒ ∑ j w ′ ( F i , F j , p i , p j ) x j ∈ R 1 × D ⇒ softmax ( ( x i W q ) ⋅ ( x W k ) ⊤ + P i ) x ∈ R 1 × D \begin{align} \psi_p(x_i, x_j) &= \mu(x_i, x_j) f(x_i, x_j) g(I_i, I_j), h(p_i, p_j) \\ & \Rightarrow \mu(x_i, x_j) w(\mathcal{F}_i, \mathcal{F}_j, p_i, p_j)||x_i - x_j|| \\ & \Rightarrow w_s(\mathcal{F}_i, \mathcal{F}_j, p_i, p_j)x_i + \mu(x_i, x_j)w_o(\mathcal{F}_i, \mathcal{F}_j, p_i, p_j)x_j \\ \Rightarrow \psi_{p_i} & = \sum_j \psi_p(x_i, x_j) \\ & \Rightarrow \sum_j [ w_s(\mathcal{F}_i, \mathcal{F}_j, p_i, p_j)x_i + \mu(x_i, x_j) w_o(\mathcal{F}_i, \mathcal{F}_j, p_i, p_j)x_j ] \\ & \Rightarrow w_s'(\mathcal{F}_i, \mathcal{F}_j, p_i, p_j)x_i + \sum_{j \ne i} w_o(\mathcal{F}_i, \mathcal{F}_j, p_i, p_j)x_j \\ & \Rightarrow \sum_{j} w'(\mathcal{F}_i, \mathcal{F}_j, p_i, p_j)x_j \in \mathbb{R}^{1 \times D} \\ & \Rightarrow \text{softmax}((\mathbf{x}_iW_q) \cdot (\mathbf{x}W_k)^\top + P_i) \mathbf{x} \in \mathbb{R}^{1 \times D} \\ \end{align} ψp(xi,xj)⇒ψpi=μ(xi,xj)f(xi,xj)g(Ii,Ij),h(pi,pj)⇒μ(xi,xj)w(Fi,Fj,pi,pj)∣∣xi−xj∣∣⇒ws(Fi,Fj,pi,pj)xi+μ(xi,xj)wo(Fi,Fj,pi,pj)xj=j∑ψp(xi,xj)⇒j∑[ws(Fi,Fj,pi,pj)xi+μ(xi,xj)wo(Fi,Fj,pi,pj)xj]⇒ws′(Fi,Fj,pi,pj)xi+j=i∑wo(Fi,Fj,pi,pj)xj⇒j∑w′(Fi,Fj,pi,pj)xj∈R1×D⇒softmax((xiWq)⋅(xWk)⊤+Pi)x∈R1×D
- F \mathcal{F} F表示模型提取的特征图。
对于每个节点 x i x_i xi,原始的pairwise potential function转变成了全局节点的线性组合,只是组合的权重与涉及的两个节点的特征和位置有关。上面式子10这一形式与QKVAttention的计算过程11是非常相似的,只是需要额外在QK的计算过程中添加上位置信息。
模型细节
- 每个CRF中计算时使用的窗口大小为7x7。
- 每个解码器在基于Attention的CRF的处理后,会使用
nn.PixelShuffle来上采样特征。 - 训练损失为Scale-Invariant Logarithmic (SILog) loss。
对比实验



 意识到 MatterPort3D 的训练集数量很少,所以作者们在现实世界中收集了更多的数据。使用 50K 图像对网络进行预训练,然后在 MatterPort3D 训练集上对其进行微调,从而获得更好的性能,如表 4 所示。使用更多数据进行预训练的模型用“Ours*”表示。这证明了具有更多图像的预训练可以清晰的促进深度估计的性能。
意识到 MatterPort3D 的训练集数量很少,所以作者们在现实世界中收集了更多的数据。使用 50K 图像对网络进行预训练,然后在 MatterPort3D 训练集上对其进行微调,从而获得更好的性能,如表 4 所示。使用更多数据进行预训练的模型用“Ours*”表示。这证明了具有更多图像的预训练可以清晰的促进深度估计的性能。
消融实验

在基本的神经 FC-CRFs 结构之上,我们添加了基于重排的上采样模块。从这个模块获得的性能提升并不大,但是视觉上输出的深度图边缘更锐利,网络的参数减少了。
PPM 聚合全局信息,这是窗口 FC-CRF 所缺乏的。这个模块可以帮助一些仅用局部信息难以估计的区域,例如复杂的纹理和白墙。从表 5 的结果中,我们看到这个模块有助于我们框架的性能。



