对于pytorch中nn.CrossEntropyLoss()与nn.BCELoss()的理解和使用
在pytorch中nn.CrossEntropyLoss()为交叉熵损失函数,用于解决多分类问题,也可用于解决二分类问题。
BCELoss是Binary CrossEntropyLoss的缩写,nn.BCELoss()为二元交叉熵损失函数,只能解决二分类问题。
在使用nn.BCELoss()作为损失函数时,需要在该层前面加上Sigmoid函数,一般使用nn.Sigmoid()即可,
而在使用nn.CrossEntropyLoss()其内部会自动加上Sofrmax层。下面会详细说明。
nn.CrossEntropyLoss()
nn.CrossEntropyLoss()的计算公式如下:
其中x为输入也是网络的最后一层的输出,其shape为[batchsize,class],log以e为底,,class为类别索引。
例如,输入x=[[4,8,3]],shape=(1,3),即batchsize=1,class=3,我们首先计算一下。
loss(x,0)=-x[0]+log(exp(x[0])+exp(x[1])+exp(x[2]))=-4+log(exp(4)+exp(8)+exp(3))=-4+8.0247=4.0247
loss(x,1)=-x[1]+log(exp(x[0])+exp(x[1])+exp(x[2]))=-8+log(exp(4)+exp(8)+exp(3))=-8+8.0247=0.0247
loss(x,2)=-x[2]+log(exp(x[0])+exp(x[1])+exp(x[2]))=-3+log(exp(4)+exp(8)+exp(3))=-3+8.0247=5.0247
可以看到loss(x,1)的损失函数最小,也即网络输出为第1类(0表示第0类,1表示第1类,2表示第2类)可能性最大。
loss(x,1)的损失函数最大,则网络输出为第2类的可能性最小。
可以知道若网络的输出为x=[[4,8,3]],而对应的标签为1,则得到损失函数loss=0.0247。
我们在计算机上实现一下:
import torch
from torch import nn
a=torch.Tensor([[4,8,3]])
y=torch.Tensor([2.]).long()
print(a.numpy())
print(y.numpy(),y.type())
criteon = nn.CrossEntropyLoss() #nn.CrossEntropyLoss会自动加上Sofrmax层。
loss = criteon(a, y)
print("loss=",loss.item())
y1=torch.Tensor([1.]).long()
y2=torch.Tensor([0.]).long()
print("loss1=",criteon(a, y1).item())
print("loss2=",criteon(a, y2).item())
输出结果为:
[[4. 8. 3.]]
[2] torch.LongTensor
loss= 5.024744987487793
loss1= 0.024744924157857895
loss2= 4.024744987487793
跟上面手动计算的基本一致,值得注意的是nn.CrossEntropyLoss()的参数中,第一个参数为网络的输出结果,类型为FloatTensor
第二个参数为标签,为LongTensor类型
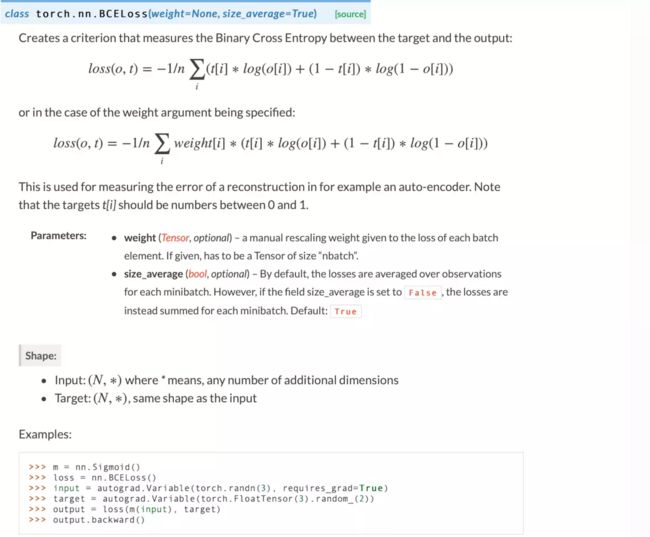
nn.BCELoss()
参考nn.BCELoss()的英文源码
计算公式如下:
t[i]—— 表示样本i的label,正类为1,负类为0
o[i]—— 表示样本i预测为正的概率,是神经网络的输出,再通过softmax,log以e为底。
例如,神经网络的输出结果为x=[6,3,-4,6],我们很容易发现,batchsize=4,通过softmax得到o=[0.9975, 0.9526, 0.0180, 0.9975]
lable=[1,0,0,1]通过公式手动计算loss:
r1 = 1 * log(0.9975) + (1-1) *log(1 - 0.9975)=-0.002503130218118477
r2 = 0 * log(0.9526) + (1-0) *log(1 - 0.9526)=...
r3 = 0 * log(0.0180) + (1-0) *log(1 - 0.0180)=...
r4 = 1 * log(0.9975) + (1-1) *log(1 - 0.9975)=...
loss=(-1/4)(r1+r2+r3+r4)=0.7680758203362535
在计算机上使用nn.BCELoss()实现:
import torch
import numpy as np
from torch import nn
a=torch.Tensor([6,3,-4,6])
y=torch.Tensor([1,0,0,1])
print(a.numpy())
print(y.numpy(),y.type())
criteon = nn.BCELoss()
pred=nn.Sigmoid()(a)
print("pred=",pred)
loss = criteon(pred, y)
print("loss=",loss.item())
输出结果如下:
[ 6. 3. -4. 6.]
[1. 0. 0. 1.] torch.FloatTensor
pred= tensor([0.9975, 0.9526, 0.0180, 0.9975])
loss= 0.7679222226142883
可以看到与手动计算的loss,相差不大,对于nn.BCELoss()的输入其第一个参数为神经网络nn.Sigmoid()的输出,第二个参数为FloatTensor类型。
![\large loss(x,class)=-log(\frac{exp(x[class]))}{\sum_{i}exp(x[i]}) =-x[class]+log(\sum_{i}exp(x[i]))](http://img.e-com-net.com/image/info8/66486c9e026e4b1497b6e1c62cbdbf63.gif)
![\large loss(o,t)=-1/n\sum_{i}^{n}(t[i]*log(o[i])+(1-t[i])*log(1-o[i]))](http://img.e-com-net.com/image/info8/e7f86fe8d25e459d9d94db9db45c3765.gif)